三相非正弦多重矢量功率理论

李 琳， 于静茹， 孙佳安

(新能源电力系统国家重点实验室(华北电力大学)， 北京 102206)

0 引 言

随着电力电子装置等非线性设备在电力系统中的广泛应用，谐波和无功补偿问题日益严重[1]。在非正弦条件下，传统功率定义不再适用，这也给系统的状态评估、无功补偿方案的设计等造成了很大的难题[2]。

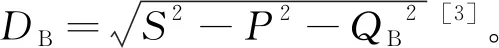
直到20世纪中后期，电力电子技术的发展激发了人们对于非正弦功率理论的思考[10，11]，众多学者相继提出了非正弦条件下的功率理论[12-31]。Shepherd和Zakihani定义有功电流iR与Fryze定义一致，无功电流iX定义为与电压波形相移90°的电流分量，二者相互正交，其与电压的乘积分别定义为有功视在功率SR和无功视在功率SX，进而得到视在功率方程S2=SR2+SX2。如果负载是非线性的，电流的分解不变，只需增加畸变视在功率SD，将视在功率方程修正为[12]S2=SR2+SX2+SD2。但该方法定义的无功视在功率与无功功率没有明确的对应关系，相关的功率定义不准确，功率现象也难以描述。随后D.Sharon对其进行改进和修正，但所定义的补充无功功率依然没有清晰的物理意义[13]。Kusters和Moore修正了Fryze定义，进一步将除有功电流以外的电流分量划分为感性(容性)无功电流和剩余电流，其中感性(容性)无功电流iql(iqc)定义为同等电压下，电感(电容)元件中流过的等效电流，其余为剩余电流ilr(icr)，这样就将视在功率划分为有功功率P、无功功率Ql(Qc)和剩余无功功率Qlr(Qcr)[15]。但该定义方法是从单个电感或电容支路无功补偿出发，无功功率的定义并不具有普适性。

为了解决非正弦下三相系统的无功补偿问题，1984年Akagi在时域下建立了三相瞬时无功理论[17]，它通过将三相电压、电流的瞬时值变化到另一正交系上，从而计算出瞬时的有功功率和无功功率。该理论一般需要通过检测无功电流来补偿无功，在有源滤波器(APF)等电力电子装置中得到了比较成功的运用[32]。但该瞬时无功功率是不同轴上电压与电流的乘积之和，仅表示系统各相之间交换的能量大小，并不能描述负载与电源之间的能量流，不能很好地解释相关的功率现象，物理意义也不够清晰，只适用于三相系统，仅仅是一种“实用性”的功率理论[33]。

2008年，Czarnecki提出了电流物理分量(Currents’ Physical Components，CPC)功率理论[30]。其中有功电流iF与Fryze定义一致，由于各次谐波下的负载电导不同于负载等效电导而产生的电流分量定义为分散电流is，无功电流ir定义为与电压波形相移90°的电流分量。如果负载是非线性的，电流中可能出现不同于电压谐波频率的谐波电流，这部分电流分量定义为发生电流iC。各个电流分量相互正交，都对应着明确的物理现象。通过电流的正交分解i=iF+is+ir+iC，功率成分也得到相应的划分S2=P2+Ds2+Qr2+DC2。但该方法分解复杂，忽略了系统电源内阻，在实际不平衡系统中各分量的正交性并不确定，其应用十分受限[34]。

即便存在着很多的功率理论，但在非正弦条件下，无功功率的定义仍然没有在数学表达与物理意义上达到统一[1]，单相电路与三相电路之间也相互独立[35]，功率理论并没有被大众普遍接受。2007年，希腊学者Menti首次提出在单相电路中利用几何代数法(Geometric Algebra，GA)将电压与电流的几何积定义为多重矢量功率(Power Multivector)[36]，其中内积为一个标量(Scalar)，该部分对应于有功功率；外积由二重矢量(Bivector)组成，每个二重矢量表征着有向平面，其大小等于平面的面积，该部分对应于非有功功率。与传统基于复数定义的视在功率相比，基于几何代数法定义的多重矢量功率可以提供更多的信息—功率方向(坐标正负)和形成原因(不同频次间或不同相间组成的二重矢量)，因此更适合应用在非正弦条件下。但是，Menti提出的多重矢量功率仅针对单相线性电路进行讨论，也没有划分不同的功率成分。2009年，Lev-Ari学者首次将几何代数法应用于多相系统[37，38]，建立了多相系统多重矢量功率的初步概念，但未能对其在实际系统中的适用性作出说明或验证。

本文在以上学者建立的多重矢量功率基础上，根据电压的频率成分及相角建立基矢量，进而形成电压和电流矢量，二者的几何积定义为多重矢量功率，对其成分划分为有功功率、分散功率、Budeanu无功功率、畸变无功功率和相间不平衡功率五类，建立了多重矢量功率理论。该功率理论适用于非正弦单相与三相电路，能够为非正弦下的无功功率提供辨识与分析。最后通过具体算例和仿真实验，验证了该方法的有效性。

1 几何代数及功率的几何积表示

1.1 几何代数

在十九世纪末，Clifford和Grassmann提出一种新的数学工具—几何代数，随后经Hestenes完善[39]。以一个n维矢量空间为例，选定一组正交基矢量{e1,e2,…,en}，则该空间内任意两个矢量可表示为

(1)

定义两个矢量的内积和外积分别为

(2)

式中：‖·‖表示矢量的模(大小)，θ表示两个矢量之间的夹角，两个矢量作内积的结果是一个标量；外积满足反交换律a∧b=-b∧a，两个矢量的外积a∧b为矢量a沿矢量b扫过的有向平行四边形区域，其结果是一个二重矢量，大小为该平面的面积[38]。

定义两个矢量的几何积为

(3)

几何积的结果为一个多重矢量，它等于两矢量的内积与外积之和，〈·〉k为多重矢量的k重矢量。通过乘法和加法运算，矢量生成了一个更大的线性空间—几何代数域Gn，它在加法和乘法下是封闭的，且乘法的规则是几何积。多重矢量的模为

(4)

式中：(·)*为多重矢量的反转(Reverse)，对于一阶矢量，其反转类似于复数中的共轭运算，多重矢量的反转计算为

(5)

在多重矢量的计算过程中，一组正交基矢量之间满足以下关系：

eiei=ei·ei+ei∧ei=1+0=1，∀i

eiej=ei·ej+ei∧ej=ei∧ej=eij=-eji，i≠j

(6)

几何代数可以在任意维空间下作多重矢量运算，它还可以将向量、矩阵、四元数、复数等代数系统统一起来，是个强大又灵活的工具，目前已经成功地应用于工程和科学领域等[39，40]。

1.2 功率的几何积表示

在具有非正弦周期性电压和电流波形的单相电路中，根据电压和电流的频域分解，在n维几何代数域Gn内，将其表示为正交基函数线性组合的形式：

(7)

式中：ej(t)为正交基函数，由于基函数的正交性质，有

(8)

x矢量的模‖x‖与x(t)的均方根值‖x(t)‖一致。

功率可以表示为电压和电流矢量的几何积所产生的多重矢量：

(9)

式中：内积产生的标量部分代表有功功率P(Active power)；外积产生的二重矢量部分代表非有功功率N(Non-active power)。进一步可以将有功功率P、非有功功率N分别表示为

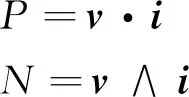
(10)

多重矢量功率S的大小为

(11)

由上式可知，多重矢量功率S的大小等于视在功率。

基于几何代数法，将非正弦下功率表示为多重矢量，而不再以简单的复数形式表示，在矢量空间内满足守恒定律[36]。由于基矢量与时域函数的对应关系，使视在功率多重矢量和瞬时功率方程之间相互统一。简而言之，非正弦情况下的多重矢量功率可以理解为正弦情况下的复功率的推广。

2 多重矢量功率理论

2.1 单相电路

设电压是非正弦周期函数，且满足Dirichlet条件，经过Fourier分解，可以将其表示为

(12)

式中：NV为计算中考虑的电压最大谐波次数；ω为基波角频率；Vk、φk分别为k次谐波下电压的有效值和相角。

根据电压的频域分解结果，选取基矢量及其扩展基矢量：

(13)

式中：伪标量J为虚数，表示顺时针旋转90°，且J2=-1。

在几何代数域内，电压矢量可表示为

(14)

经过Fourier分解，将电流表示为

(15)

式中：NI为计算中考虑的电流最大谐波次数；Ik、ψk分别为k次谐波下电流的有效值和相角。

电流中可能出现不同于电压谐波子集的谐波电流子集，这部分电流分量是由非线性负载引起的，定义其为带外电流(out-of-band current)i⊥[37]。i⊥包含多个谐波分量，成分复杂，为了将电流统一表示为正交基线性组合的形式，这里引入基矢量e⊥，它与式(13)中的基矢量相互正交，其坐标(大小)为I⊥。

在几何代数域内，电流矢量可表示为

(16)

带外电流i⊥的大小满足：

(17)

各次谐波下，与电压波形相似且同相位的电流分量定义为平行电流ip(parallel current)；与电压波形相移90°的电流分量定义为正交电流iq(quadrature current)，其表达式分别为

(18)

Fryze有功电流iF定义为[4]

(19)

式中：iF为负载消耗有功功率所需的最小电流；P为系统的有功功率；Ge为负载的等效电导。由于各频率下的负载电导Gk不同于等效电导Ge而产生的电流分量定义为分散电流(scattered current)is，它是平行电流ip中除去有功电流iF以外的电流分量[34]；而无功电流ir定义为与电压相移90°的电流分量[12]，即

(20)

因此，在非线性条件下，电流的正交分解为

(21)

将上式代入到式(9)中，进而可以将多重矢量功率划分为

(22)

式中：Ds表示各频率下负载电导不同于等效电导而产生的分散功率；QB表示各频率下的Budeanu无功功率；Qh表示不同频次的电压和电流谐波相互作用产生的畸变无功功率；Q⊥表示负载非线性引起的无功功率。

将电压、电流矢量表达式(14)和(16)代入式(22)中，得到各部分功率的具体表达式如下：

Qh=v∧(ir(-J))=

(23)

多重矢量功率S的大小满足：

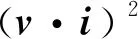
(P)2+‖Ds‖2+(QB)2+

‖Qh‖2+‖Q⊥‖2

(24)

2.2 三相电路

在三相电路中，将三相电压和电流写为

(25)

式中：v和i分别为三相电压和电流所组成的列向量，va,b,c为三相电压，ia,b,c为三相电流。设电压是非正弦周期函数，且满足Dirichlet条件，经过Fourier分解，可以将其表示为

(26)

式中：l为三相标识，ηl为3维列向量，l=a,b,c时分别对应向量中第1,2,3项为1，其余为0，Vl,k、φl,k分别为l相k次谐波下电压的有效值和相角。

根据电压的频域分解结果，选取基矢量及其扩展基矢量：

(27)

在几何代数域内，电压矢量可表示为

(28)

经过Fourier分解，将电流表示为

(29)

式中：Il,k、ψl,k分别为l相k次谐波下电流的有效值和相角。

同理，三相系统中平行电流ip、正交电流iq、带外电流i⊥为各相电流分量的矢量和，因此这三个分量也相互正交。在几何代数域内，电流矢量可表示为

(30)

将电压、电流矢量表达式(28)和(30)代入式(22)中，得到l相中各部分功率的具体表达式如下：

Sl=Pl+Ds,l+QB,lJ+Qh,lJ+Q⊥,l

‖Sl‖2=(Pl)2+‖Ds,l‖2+(QB,l)2+

‖Qh,l‖2+‖Q⊥,l‖2

(31)

式中：Pl表示l相有功功率；Ds,l表示l相中各频率下负载电导不同于等效电导而产生的分散功率；QB,l表示l相在各频率下的Budeanu无功功率；Qh,l表示l相中不同频次的电压和电流谐波相互作用产生的畸变无功功率；Q⊥,l表示l相中负载非线性引起的无功功率；Sl表示l相多重矢量功率。

需要注意的是，以上的功率分量是由单相电路扩展而来，是a,b,c各相的功率，而当三相电路不平衡时，功率不仅在电源与负载间流动，而且还在各相间流动[35]。因此在三相电路中功率还需包括相间不平衡功率Dn，在形式上可以将其表示为

(32)

式中：Dn由各相电压与不同相电流之间的外积产生，Dab为ab相的相间功率，方向为a相流向b相，且Dba=-Dab，bc相与ca相的相间功率同理。Dn的大小为

(33)

三相多重矢量功率S满足：

S=Sa+Sb+Sc+Dn

‖S‖2=‖Sa+Sb+Sc‖2+‖Dn‖2

(34)

可以看出，在非正弦条件下，通过引入表示相间功率的多重矢量，可将多重矢量功率的概念从单相电路扩展到三相电路，实现单相与三相电路相统一。该理论根据电压的频域分解结果建立基矢量，即使在电压畸变的情况下，也可以得到电流相对于电压的广义谐波，直观地提供负载的线性程度信息，从而把该功率理论与谐波理论相联系[35]。各功率成分能够被准确划分，物理意义明确，有利于对谐波和无功功率进行辨识与分析，为谐波抑制和无功补偿提供理论支撑。

3 多重矢量功率分析

为更好说明以上理论，下面分别对单相电路、三相电路和三相三线制系统进行功率分析计算。

3.1 单相电路

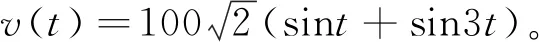
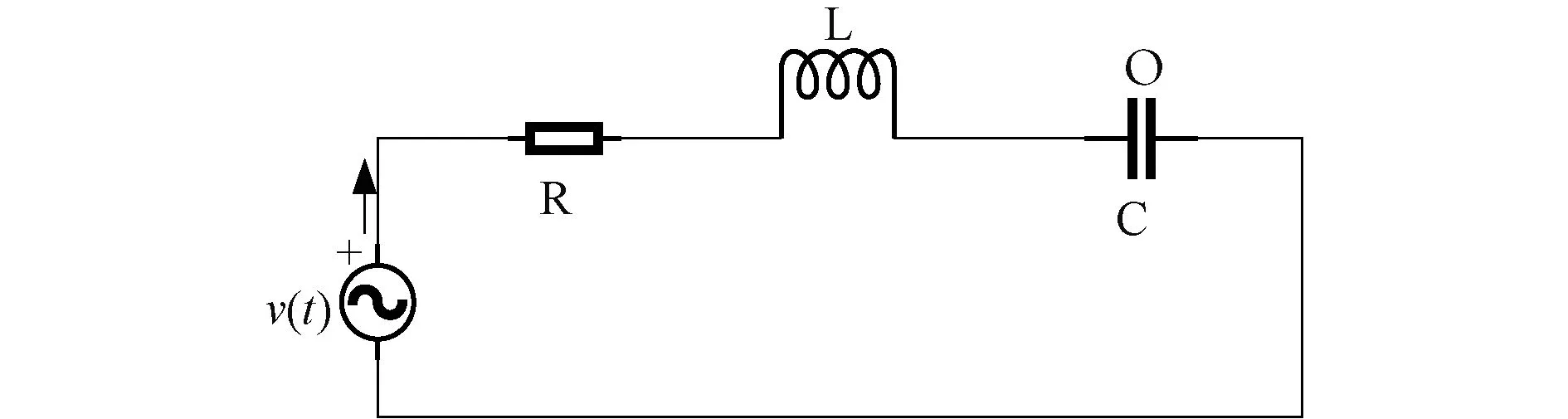
图1 单相RLC电路

v=v1+v3=100e1+100e3

(35)

在几何代数域内，k次谐波下的阻抗表示为[41]

(36)

那么，基波和3次谐波阻抗和导纳分别为

Z1=1-3e1e1J→Y1=0.1+0.3e1e1J

Z3=1+0.33e3e3J→Y3=0.9-0.3e3e3J

(37)

因此，电流可以表示为

i=i1+i3=Y1v1+Y3v3

=10e1+30e1J+90e3-30e3J

(38)

多重矢量功率S经计算得

S=vi

=10+8e1e3+(3e1e1J-3e3e3J)+

(-3e1e3J-3e1Je3)

=P+Ds+QBJ+QhJ

(39)

在该算例中，有功功率P为10 kW，其余为非有功功率N，它包括分散功率Ds、Budeanu无功功率QB和畸变无功功率Qh。多重矢量功率S的大小为

(40)

电流矢量的计算结果如表1所示。

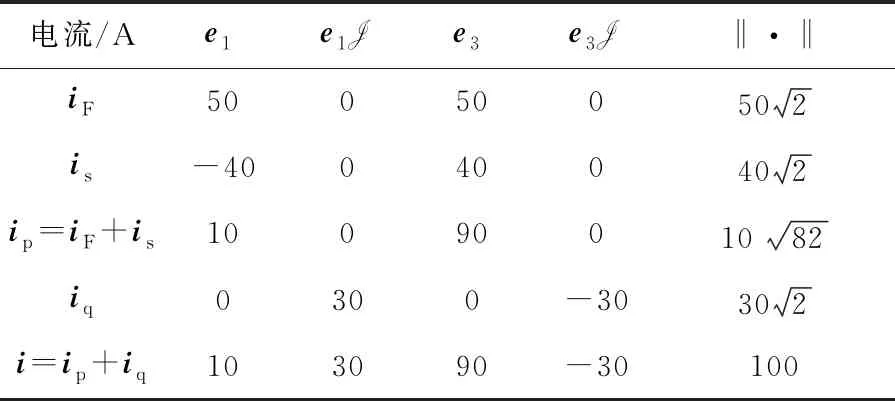
表1 图1中电流矢量的计算结果

CPC理论通过电流的正交分解，可以清晰地表征电流的物理意义，目前备受关注[34,42]。若采用电流物理分量(CPC)理论计算功率[30]，则有功功率P、分散功率Ds和无功功率Qr分别为

(41)

通过以上两种功率理论得到各部分功率分量的计算结果，如表2所示。

表2 图1中各功率计算结果

由表2可知，多重矢量功率理论中各功率分量根据式(4)求得的模值与CPC理论中对应的功率分量相同。相比而言，CPC理论中各部分功率仅是一个数值，不能进行矢量运算；而多重矢量功率理论可以准确对各功率成分进行数学表示，解决了非有功功率的运算问题。

3.2 三相电路

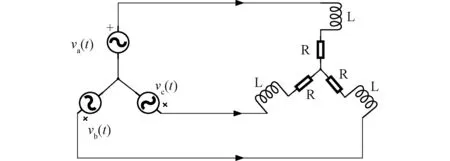
图2 三相RL电路

根据本文方法建立正交基，在几何代数域内，将三相电压表示为

(42)

每一相阻抗和导纳相同，基波和2次谐波阻抗和导纳分别为

Z1=0.707+0.707e1e1J→

Y1=0.707-0.707e1e1J

Z2=0.707+1.414e2e2J→

Y2=0.283-0.566e2e2J

(43)

因此，电流可以表示为

i=i1+i2=Y1v1+Y2v2=

162.63ea,1+162.63eb,1+162.63ec,1+

(162.63ea,1+162.63eb,1+162.63ec,1)J+

31.11ea,2+31.11eb,2+31.11ec,2+

(62.22ea,2+62.22eb,2+62.22ec,2)J

(44)

由于三相负载线性平衡，不存在相间不平衡功率Dn。这里给出a相多重矢量功率，如式(45)所示，b、c相同理。

=Pa+Ds,a+QB,aJ+Qh,aJ

(45)

计算出各功率分量的大小分别为

P=40.83×3=122.49

‖Ds‖=10.73×3=32.19

QB=(37.41+6.85)×3=132.78

‖Qh‖=(17.89-14.31)×3=10.74

‖S‖=‖v‖‖i‖=441.59×416.18=183.78

(46)

这里考虑的情况只涉及基波和一个谐波，但只要选择适当的几何代数域，同样的分析也可以很容易地扩展到涉及任意数量谐波的一般情况。

3.3 三相三线制系统

在图3所示的三相三线制系统中，阻抗用于模拟线性负载，三相不可控整流装置用于模拟非线性负载。根据负载特性和电压谐波情况，选取12种工况，算例的具体参数如表3所示。三相电压对称，这里仅表示a相电压，有正弦i和非正弦ii两种形式。通过MATLAB/Simulink仿真，对不同的功率分量进行分析研究，得到功率的具体计算结果如表4所示。

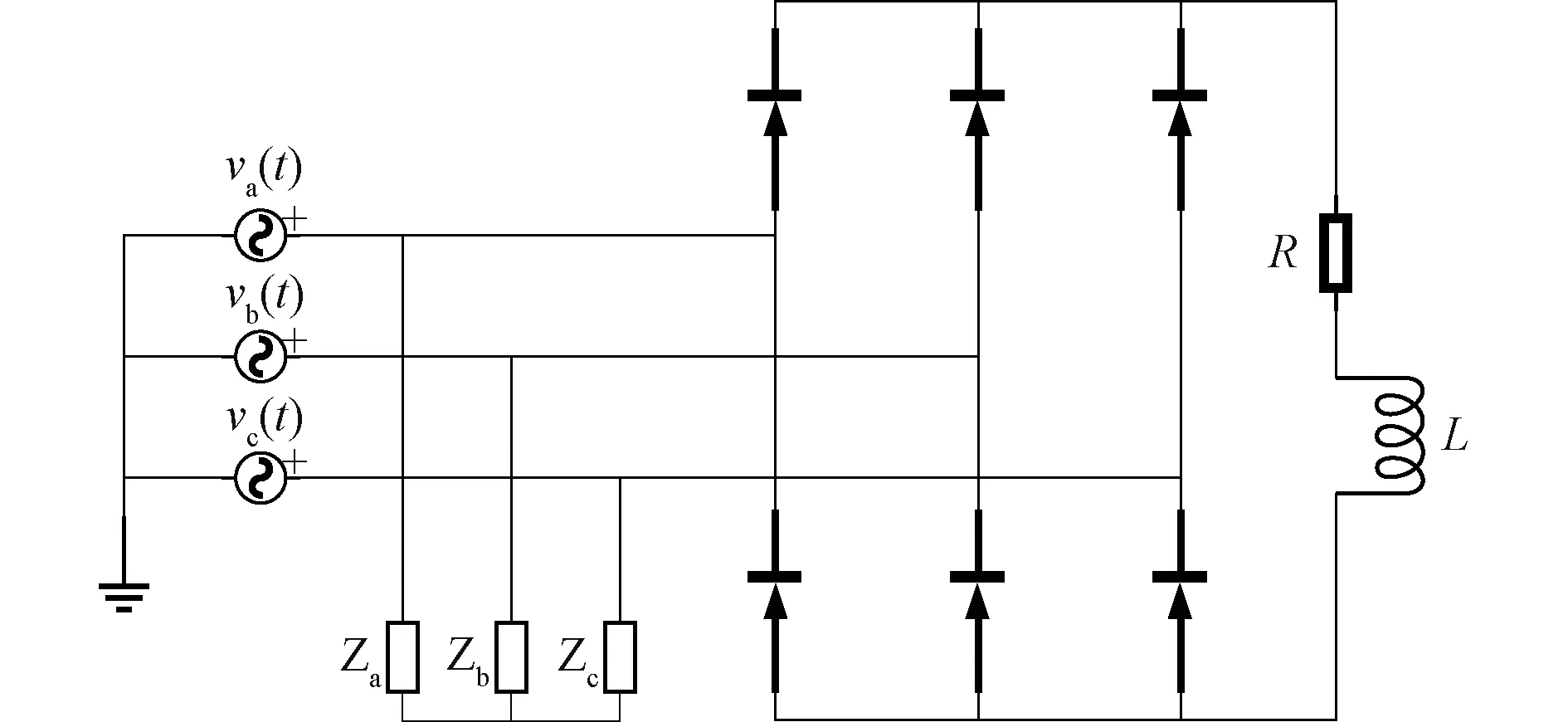
图3 算例拓扑结构

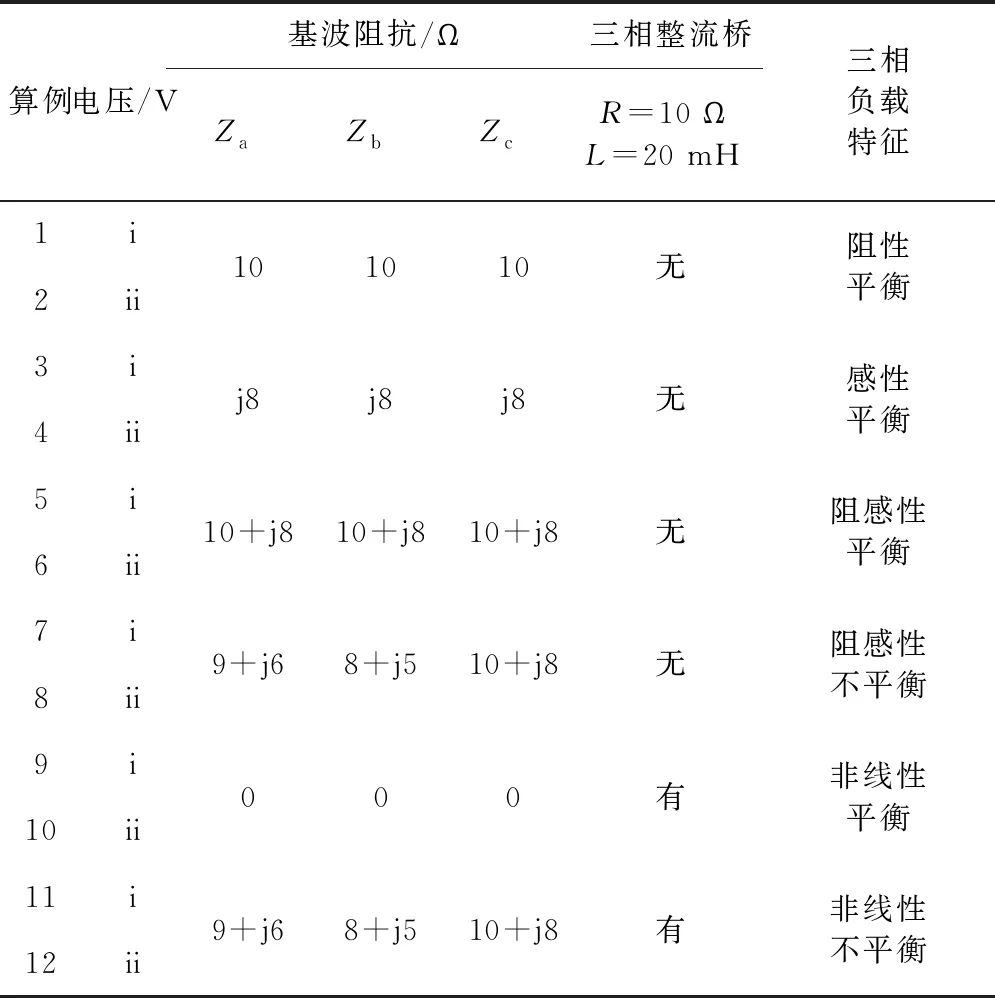
表3 算例参数

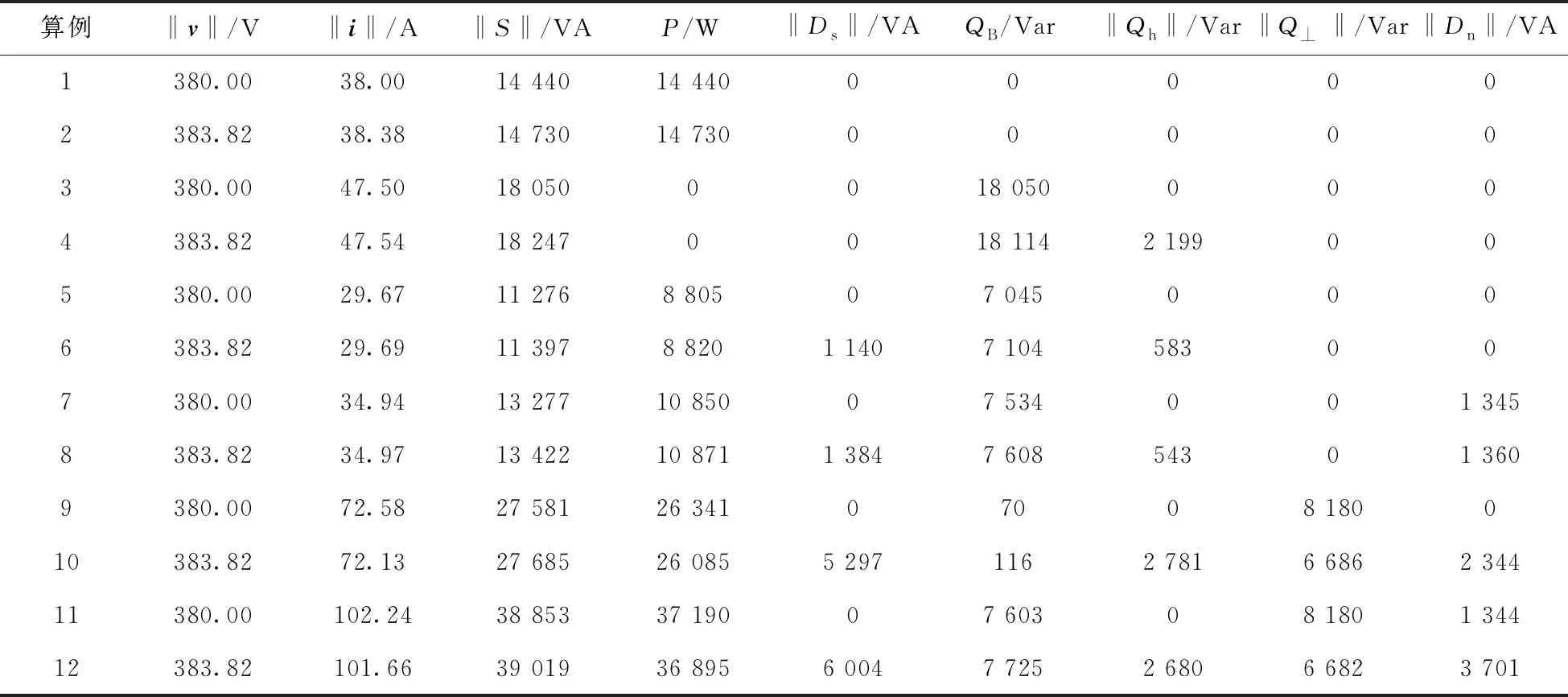
表4 各算例的功率计算结果

以算例12为例，具体写出电压、电流的表达式如下：

v=219.42ea,1+219.42eb,1+219.42ec,1+

21.94ea,5+21.94eb,5+21.94ec,5+

21.94ea,7+21.94eb,7+21.94ec,7

i=60.52ea,1+55.05eb,1+51.73ec,1+

(9.56ea,1+16.54eb,1+8.31ec,1)J-

0.56ea,5+8.78eb,5+7.66ec,5+

(0.67ea,5-3.43eb,5+6.71ec,5)J-

4.07ea,7-1.80eb,7-1.51ec,7+

(1.52ea,7-0.14eb,7+2.66ec,7)J+

11.76ea,⊥+9.04eb,⊥+9.35ec,⊥

(47)

这里给出a相多重矢量功率和各功率分量的大小，分别如式(48)和(49)所示，b、c相同理。

(48)

(49)

在该算例中，Ds(含ek1ek2项)是由于基波电导、5次谐波电导和7次谐波电导各不相同而产生的分散功率。QBJ(含ekekJ项)中包含了各相的基波、5次和7次谐波的Budeanu无功功率，k次谐波下的Budeanu无功功率是该频率下电压与无功电流之间产生的无功功率，这与频域的分析结果一致。QhJ(含ek1ek2J项)是基波、5次和7次谐波中不同频次的电压和无功电流之间产生的畸变无功功率，Q⊥(含eke⊥项)是由于存在非线性整流装置使得电流中出现其他谐波分量所形成的无功功率。可以看出，在非正弦条件下，非有功功率分量不能简单地通过复数表示，更不能进行复数运算，需将复平面扩展到几何代数域，引入多重矢量功率概念解决该问题。

根据式(47)～(49)，计算出三相各功率分量和多重矢量功率的大小如下：

(50)

在非正弦多重矢量功率理论中，正交基根据电压矢量v选取，在该基矢量的坐标下形成的电流分量定义为平行电流ip。由于各次谐波下负载的电导值不相同，虽然各频率下的平行电流ip与负载电压波形相似，但所有频率下的总平行电流ip并不一定与负载电压波形相似，可以将其进一步分解为有功电流iF和分散电流is。其中有功电流iF与Fryze定义一致，它是与电压成比例的电流分量，电压与有功电流iF的内积定义为有功功率P，该有功功率的定义方法本质上与Fryze等传统功率定义保持一致。分散电流is与CPC理论中分散电流的定义一致，它是由于各次谐波下的负载电导不同于等效电导而产生的电流分量，电压与分散电流is的外积定义为分散功率Ds。由表4可知，只有当电压中存在谐波时，才可能出现分散功率。因此分散功率Ds不仅与负载的属性相关，还与电压特性相关。

各次谐波下与负载电压波形相移90°的电流分量定义为正交电流iq，它与无功电流ir定义相同，将电压与无功电流ir的内积定义为Budeanu无功功率QB。这种定义方法从几何代数的角度，说明了各次谐波下Budeanu无功功率的功率方向和符号含义，解释了其隐藏的物理意义。畸变无功功率本质上是电压和电流在不同频率下相互作用而引起的无功功率，它包含了两部分，一是无功电流ir与电压形成的外积Qh，它表征了电压谐波或电流谐波所产生的无功功率，直观反映了电压的畸变程度；二是由于传统非线性负载，使得电流产生不同于电压谐波次数的分量—带外电流i⊥，它与电压形成的外积Q⊥，直接体现了负载的非线性度。

相间不平衡功率Dn的大小是由ab相、bc相、ca相的相间功率决定的。由表4可知，当三相负载平衡且为线性时，Dn的大小为0，这说明它与三相负载之间的不平衡度有很大的关系。但在算例12中，Dn的值远大于在算例7、8和11中的值，并且算例12中Dn的值恰好为算例10(只含整流负载)下的值和算例8(只含不平衡负载)下的值之和，这说明当电源电压含谐波时，在三相整流电路中会产生不平衡分量，使Dn增大。

4 结 论

本文基于几何代数法，建立了非正弦多重矢量功率理论，对功率的成分进行了分类，并使非正弦单相与三相电路相统一。在不同算例和仿真实验下，通过多重矢量功率计算，对该理论进行深入分析，证明各功率分量在数学表达与物理意义上达到统一，为非正弦下三相系统的功率分析提供了理论基础，为电能质量评价、无功补偿等具体应用提供了新的思路。