约束间隙对气动柔性轴向驱动器伸长量的影响

苟志攀，耿德旭，刘洪波，许文智，贾 鑫

(北华大学机械工程学院，吉林 吉林 132021)

近十几年来，随着科学技术的不断发展，机器人已经进入人类生活.相较于传统的刚性机器人，使用柔性材料结合仿生机器人技术研制出的柔性机器人，因具有良好的柔顺性和适应性，以及人机交互的安全性，成为近几年机器人领域的研究热点[1-2].柔性机器人最关键的技术是柔性驱动器和末端附着装置设计，作为机器人驱动装置，柔性驱动器直接决定机器人的驱动能力[3-4].目前，主要的柔性驱动器驱动方式有绳索驱动、流体驱动、智能材料驱动、化学反应驱动及磁场驱动等[5].气压驱动是柔性机器人应用最多的驱动方式，主要有纤维约束结构、弹性腔室结构、折叠/褶皱结构和波纹管结构[6]几大类.气动柔性驱动器的原理是使用压缩气体(负压/正压)对各种结构的弹性腔室吸气或通气，驱动器在本身结构和外部约束下，在空间中向某一方向产生收缩或膨胀式运动[7](轴向缩短/伸长、扭转、弯曲及其组合运动).由于气压驱动器驱动力有限，结构不易小型化，因此，其与外界环境接触的高适应性和可塑型性等还有待继续深入研究.采用片状约束环及弹簧约束的轴向驱动器弹性腔体会沿着约束间隙径向膨胀变形，在一定程度上影响驱动器的工作性能.针对这个问题，本文采用单一变量法，通过改变弹簧间隙研究约束间隙对轴向驱动器伸长量的影响，以掌握其内在关系，完善该类驱动器伸长性能.

1 柔性轴向驱动器结构功能与基本参数

1.1 轴向驱动器结构与功能

设计的轴向驱动器由封闭气囊和弹簧约束骨架及上、下端盖连接组成，见图1.该驱动器外部嵌套弹簧约束，上端盖通过紧固螺栓，下端盖通过气动快插接头以螺纹形式连接为一个整体.

图1 轴向驱动器三维模型

驱动器制作过程：选取两种不同材料硅胶管，机械加工的密封堵头，右旋密绕弹簧及由ABS材料打印的上、下端盖.先将硅胶管与密封堵头通过钢丝扎紧密封，为保证密闭性，预先对弹性腔体进行通气试验.外部嵌套弹簧通过销钉将端盖、弹簧、堵头连接，实现径向约束.上端盖通过紧固螺栓与上堵头连接，下端盖通过气动接头与下堵头采用螺纹连接.通入压缩气体后，气囊发生膨胀变形，由于径向膨胀被弹簧约束，驱动器会沿着轴向伸长，气压越大，伸长量越大.

1.2 轴向驱动器基本参数

驱动器参数见表1.制作的驱动器本体长度为80 mm，初始有效长度为60 mm.

表1 驱动器的结构参数

2 驱动器轴向受力与形变分析

在无外部载荷情况下，通入压缩气体后，橡胶管外壁膨胀，与弹簧内壁贴合，可看作同步运动，其变形力符合线性叠加原则，且驱动器上端所受的轴向力决定了其伸长性能.驱动器受力情况见图2.

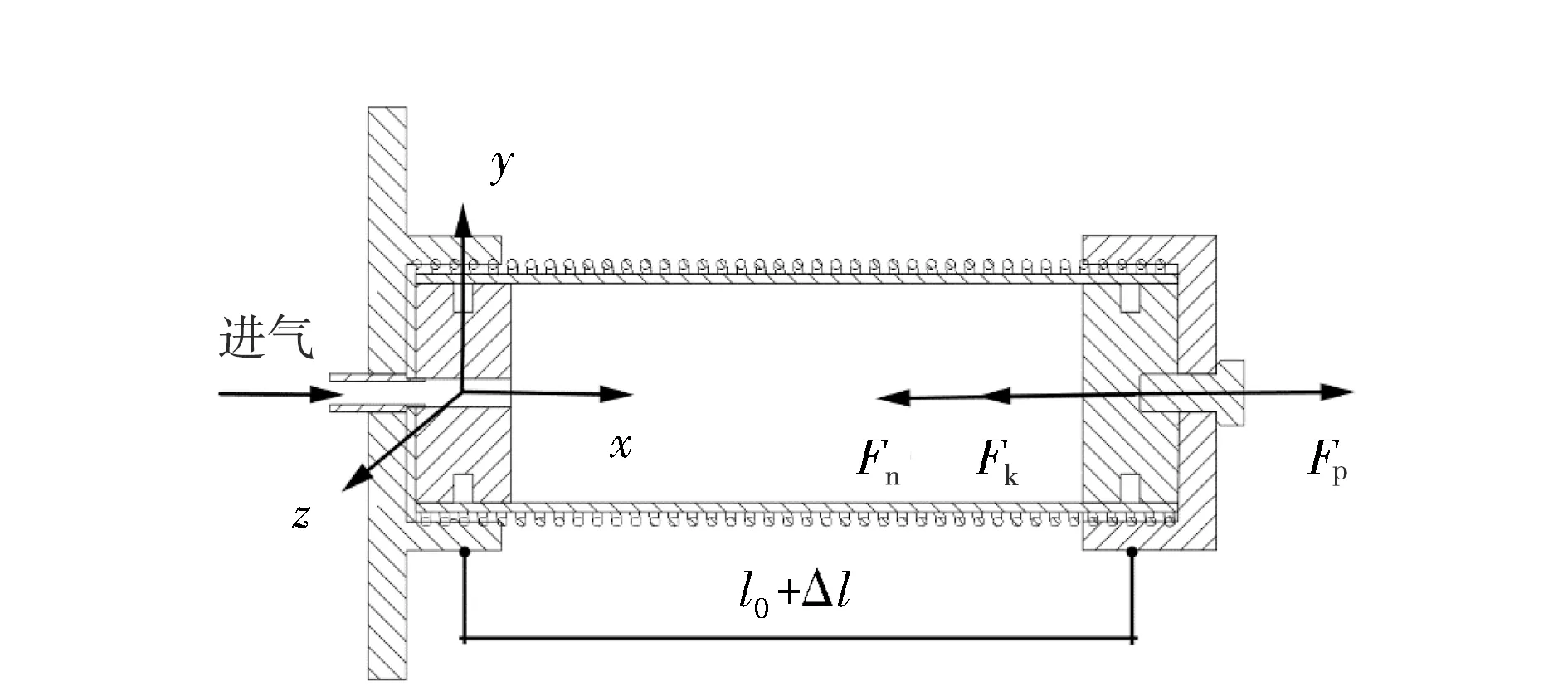
图2 驱动器轴向变形与受力分析

通气时驱动器受弹簧拉力Fk、胶管拉力Fn及驱动器上端的轴向力Fp共同作用，根据轴向静力平衡原理可知：

Fp=Fn+Fk

.

(1)

2.1 弹簧阻抗力

弹簧拉伸时产生的阻抗力阻碍驱动器伸长，选用同一种弹簧进行预拉伸会得到不同节距的弹簧，因此，弹簧的初始拉伸量随着间隙的增大而增大.设初始拉伸量为b，则根据Hooke定律，驱动器中的弹簧阻抗力为

Fk=k(Δl+b)

，

(2)

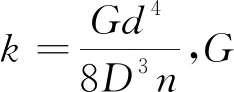
2.2 胶管阻抗力

构成驱动器的橡胶材料属于超弹性体，充压变形时各向同性，不可压缩，因此，变形前、后橡胶的总体积不变.变形前、后的几何关系见图3.

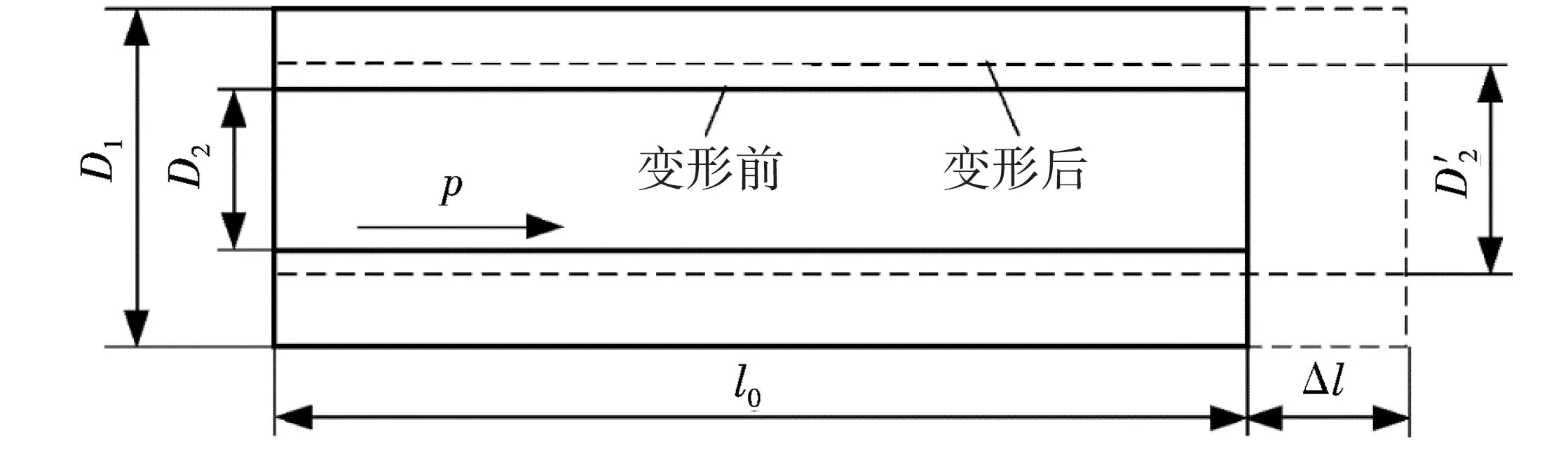
图3 轴向驱动器变形前、后的几何关系

弹簧预应力对驱动器伸长量影响较小，可以忽略不计.变形后内孔直径[8]

式中：D1、D2为橡胶管初始外、内径.

变形后驱动器橡胶管的环形截面面积为

根据圆形面积公式得该驱动器内腔横截面积为

由于驱动器伸长后弹簧间存在一定间隙，橡胶管受气压作用会沿着间隙膨胀鼓出，初始间隙和气压越大，鼓出部分越明显，这将在一定程度上增大内腔横截面积，因此，需要引入内腔横截面积的修正量ΔS[9]进行修正.修正面积与通入气压和初始间隙有关，f(x)是关于气压的函数，利用Origin软件对气压-横截面积增量试验数据拟合求导得到：

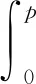
式中：a为初始约束间隙；p为通入的气体气压；C为积分常数.

修正后的内腔横截面积为

根据弹性力学经典理论，橡胶管阻抗力为

将A代入得橡胶管阻抗力为

(3)

2.3 轴向驱动力

通入压缩气体后，在驱动器上端盖附近产生的轴向驱动力随内腔工作截面变化.压缩气体在驱动器上端盖处的轴向驱动力

(4)

2.4 驱动器伸长量

将式(2)、(3)、(4)代入式(1)有

忽略高次微小量，可得伸长量表达式为

3 试验与分析

根据试验原理(图4)搭建的轴向驱动器伸长量-气压试验平台见图5.该试验平台主要由气源、精密减压阀、气压传感器、固定平台、轴向驱动器、连接件及其保持架组成.利用该试验平台研究两种不同材料的驱动器在5种约束间隙下伸长量-气压之间的关系.

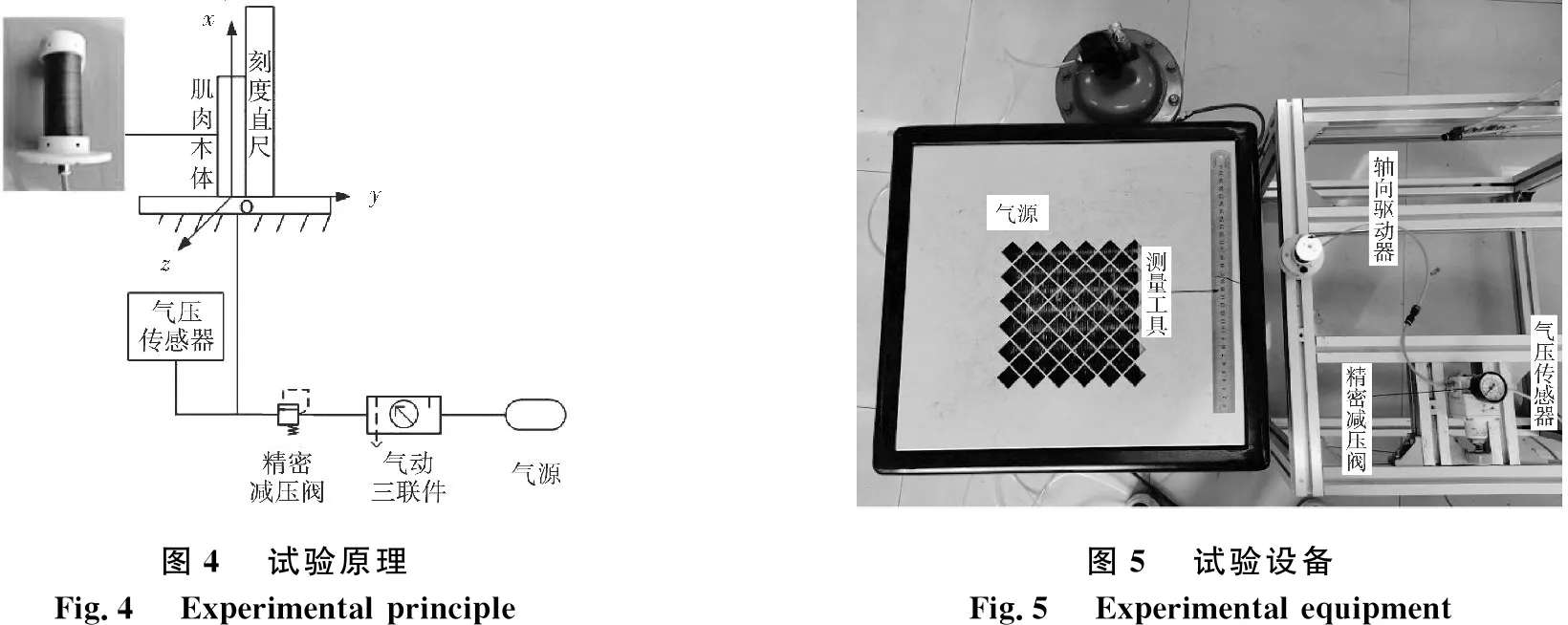
3.1 理论模型验证

为了验证所建立的伸长量-气压理论模型的正确性，选取白胶管驱动器作为验证对象，将相关参数带入理论模型，计算值与试验值对比见图6.由图6可知：理论模型计算值与试验值趋势一致，吻合较好，随着初始约束间隙增大，伸长量呈规律性变大.建立的理论模型在气压为0.2 MPa之前有较好的吻合性；在0.2 MPa之后随着通入气压的增大，误差也随之增大.主要原因是后期驱动器伸长率变小，虽然通入气压后仍会伸长，但这种伸长已不可控.将白胶管驱动器在0.2 MPa气压下对应的鼓出量定义为该类驱动器的失稳边界，具有较大的实用意义.

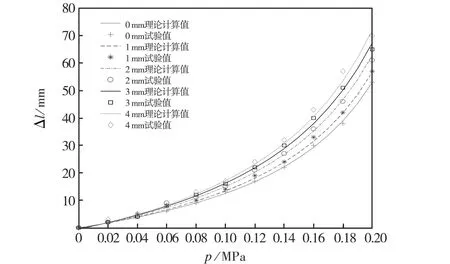
图6 白胶管驱动器伸长量理论计算与试验值

3.2 不同间隙驱动器伸长量

试验时将两组驱动器分别通气，间隔0.02 MPa采样.由于材料自身原因，灰色硅胶管通气至0.3 MPa，白色硅胶管通气至0.4 MPa.为减少试验误差，每组试验重复5次，取5次试验的平均值作为有效试验值.处理试验值并绘制曲线，见图7.由图7可见：在可控间隙内，随着约束间隙的增大，驱动器伸长量也明显增大.主要原因是随着弹簧节距的增大，径向约束之间的间隙变大，径向鼓出增大，导致驱动器截面面积增大；随着节距增大，约束弹簧螺旋升角加大，加剧了弹簧和膨胀的橡胶管之间的轴向耦合.合理增大约束间隙可以改变伸长量，但如果间隙太大，驱动器会较早失稳，如4 mm间隙的灰色硅胶管驱动器在0.24 MPa处即将失稳.

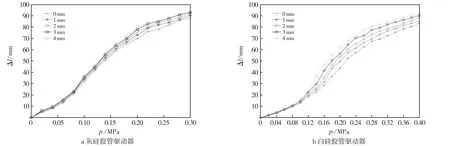
图7 不同间隙下驱动器伸长量

为了更加具体地观察驱动器在气压为0.3 MPa时的边界约束情况，对此时的约束状态进行局部放大，见图8.由图8可见：灰色硅胶管鼓出部分较明显，随着约束间隙的增大，0.3 MPa气压时鼓出部分体积逐渐变大，这主要是由材料自身硬度决定.在相同气压下，间隙越大，驱动器稳定性越差.在试验过程中发现，该类驱动器在通气伸长时存在弯曲现象，主要原因：1)制作工艺和精度不够，通气时上端面受力不均匀、倾斜造成肌肉弯曲；2)弹簧约束的驱动器通气时弹簧螺旋升角增大，引起肌肉扭转累积产生弯曲；3)硬度越小的胶管制成的驱动器越容易弯曲变形.

图8 不同间隙两组驱动器在气压为0.3 MPa时的约束情况

消除弯曲对该类驱动器的应用至关重要.解决方案：1)改善制作工艺，提高精度，解决驱动器上堵头端面受力不均问题；2)成组并联使用，安装时选用左、右螺旋两种弹簧交替安装，相互作用，抵消扭转，或者采用片状约束环的约束形式代替弹簧约束，消除弹簧升角带来的弯曲；3)选用硬度更高的硅胶管，使抗扭转和弯曲能力更强；4)增加刚性导向骨架.

3.3 相同约束间隙下驱动器伸长量

为研究胶管材料对驱动器伸长量的影响，对比在相同约束间隙下两种材料驱动器在同一气压下的伸长量，见图9.由图9可见：在同一气压下，灰色硅胶管伸长量明显大于白色硅胶管，且随着约束间隙的增大，两组驱动器伸长量差距逐渐减小，这主要是受橡胶管弹性剪切模量的影响，弹性剪切模量越大，驱动器伸长时的阻抗力越大.

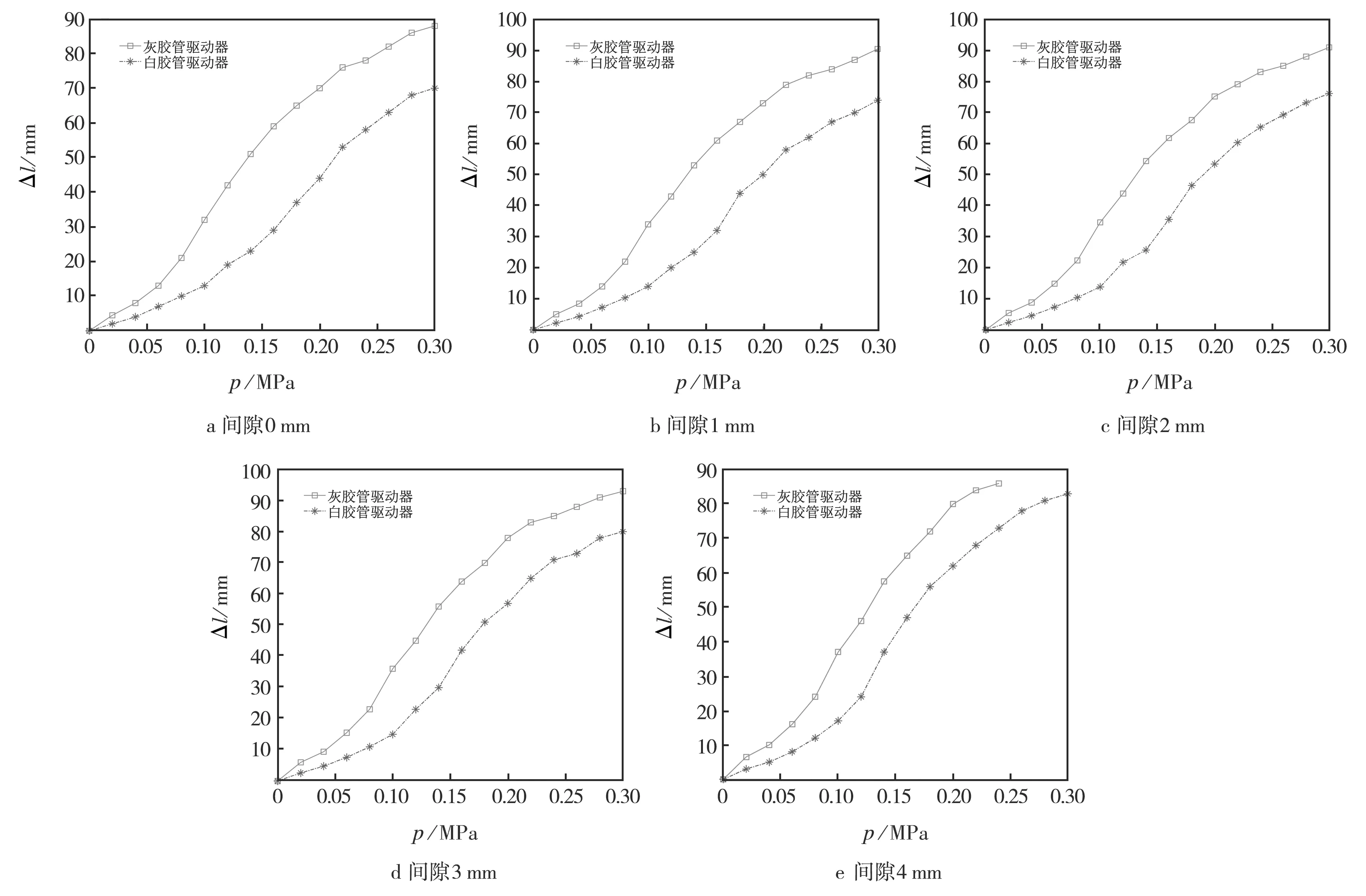
图9 相同间隙下驱动器伸长量

不同约束间隙的驱动器在气压为0.3 MPa时的伸长率见图10.由图10可知：约束间隙为0 mm时，在气压0.3 MPa下灰色硅胶管伸长率为155%，白色硅胶管为117%；间隙为1 mm时，灰色硅胶管伸长率为156%，白色硅胶管为127%；间隙为2 mm时，灰色硅胶管伸长率为158%，白色硅胶管为128%；间隙为3 mm时，灰色硅胶管伸长率为160%，白色硅胶管为133%；间隙为4 mm时，灰胶管驱动器只能通气到0.24 MPa，主要原因是当通入气压较大时约束失稳，灰胶管的非线性变形量接近最大值，此时伸长率为142%，气压为0.3 MPa时，白色硅胶管伸长率为138%.

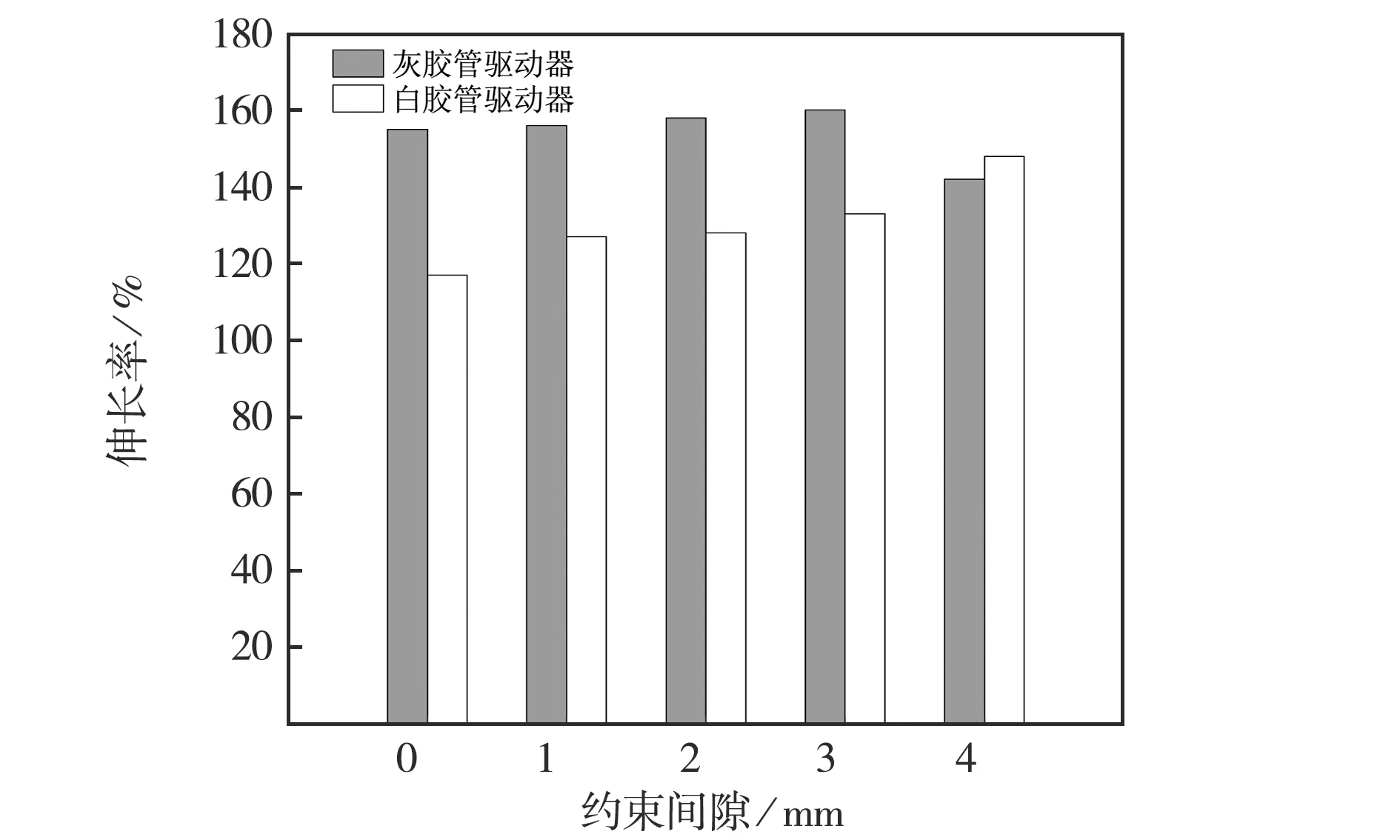
图10 不同间隙的两组驱动器在0.3 MPa气压下的伸长率

本文中驱动器的主要功能为轴向伸长，作为衡量该驱动器驱动能力的主要性能指标，轴向刚度可以用轴向驱动力与伸长量的比值来近似表示.驱动力和伸长量都与通入气压成正比，随着气压增大，驱动器伸长，其轴向刚度逐渐减小.对驱动器施加轴向载荷，当驱动力大于轴向载荷时驱动器伸长；驱动力等于载荷力时，驱动器状态保持；驱动力小于载荷时，驱动器受压.

4 小 结

本文根据橡胶经典变形理论建立了驱动器在通入气体时的形变理论模型，引入约束间隙、横截面积修正量，得到了驱动器轴向伸长量的理论模型，并进行了试验验证.采用单一变量试验法，得到以下结论：通过控制驱动器内腔气压，可以控制驱动器不同程度的轴向伸长；驱动器伸长量随着通入气体气压和约束间隙的增加而增大，但应合理设计驱动器的约束间隙.弹簧约束的轴向驱动器在通气伸长时本体会伴随一定程度的弯曲，本文提出了有效的解决办法，对于柔性驱动器的推广使用具有重要意义.将该驱动器多个并联可以制成其他运动功能的驱动器，研制的仿生柔性机器人在工业、农业领域具有广阔的应用前景.