基于自适应零极点补偿的锂电池恒流充放电算法研究与实现
2022-08-17蔡清源
蔡清源,王 阳
(浙江杭可科技股份有限公司,浙江 杭州 310011)
0 引 言
目前,锂电池广泛应用于新能源电动车、微网储能、电子产品等领域,其充放电控制已经成为近年来的重要课题[1]。锂电池充放电系统的拓扑及其控制算法一直是相关领域的研究热点,其中PID闭环控制、模糊控制以及混沌控制等策略已被广泛研究和应用[2-6]。此外,零极点补偿算法是双向降压式变换电路(Buck电路)控制的重要内容[7-9]。文献[10]提出了电压型Buck变换器的零极点补偿方法,分析了等效串联电阻(Equivalent Series Resistance,ESR)零点对环路稳定的影响,并通过实例完成了补偿器关键参数设计,但该方案使用模拟电路实现,灵活性方面具有较大的局限性。针对以上问题,本文提出了一种基于自适应零极点补偿的锂电池恒流充放电算法,实现了全电流域动态响应和稳态性能的最优化控制。
1 锂电池充放电系统电路拓扑研究
1.1 系统电路拓扑研究与分析
典型双向Buck变换电路可以实现对锂电池充放电的控制,其中线路阻抗是影响锂电池充放电系统特性的关键因素之一。实际工程中对电路拓扑进行理论分析时,需要考虑线路的电阻RLine和电感LLine,此时电路拓扑如图1所示。
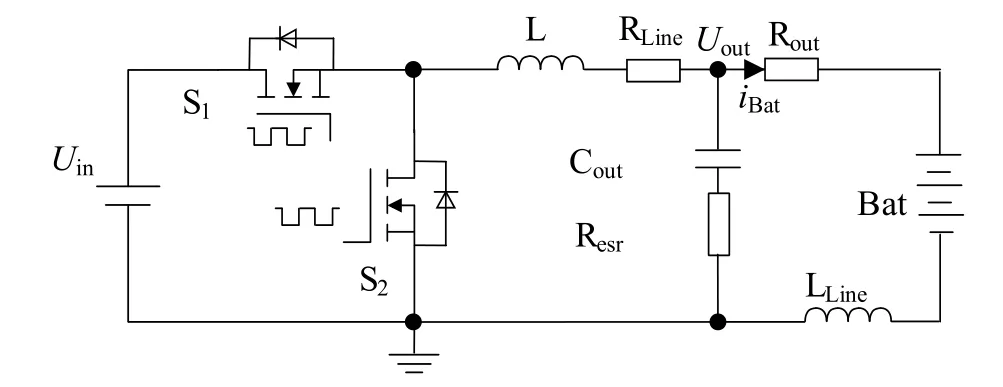
图1 双向Buck变换电路拓扑(考虑线电阻、线电感)
图中,Uin为输入电压;S1、S2为功率开关器件;L为电路的输出电感;Cout为输出电容;Resr为输出电容的等效电阻;Rout为输出等效电阻;Bat为锂电池负载。
1.2 系统主电路数学模型分析
对双向Buck变换电路数学模型进行推导分析,其为典型的三阶系统:
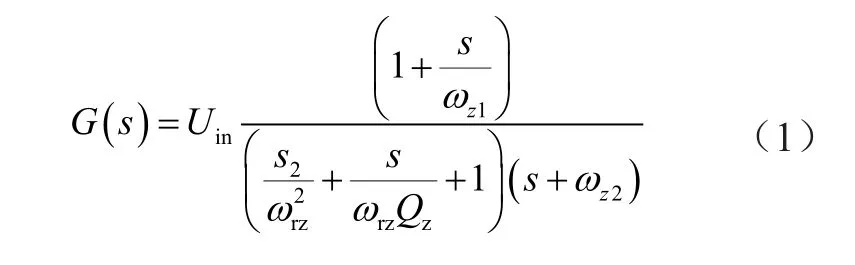
式中:Uin为电路输入电压;ωrz=2πfrz,frz为电路双极点所在的频率;Qz为电路的品质因数;ωz1=2πfz1,fz1为电路第1零点对应的频率;ωz2=2πfz2,fz2为电路第2零点对应的频率。各关键参数可以表示为:

2 锂电池充放电控制策略研究
2.1 3P3Z1CZ补偿器数字化实现研究
零极点补偿闭环控制算法在电源设计中的应用非常广泛,由于本文研究的锂电池充放电传递函数具有典型的三阶特性,因此为了完成对其稳定控制,对3P3Z1CZ补偿器进行研究。
3P3Z1CZ补偿器的传递函数为:

式中:KDC为三阶补偿器的增益;ωrz=2πfrz,frz为锂电池充放电主电路双极点所在的频率;Qz为锂电池充放电主电路的品质因数;z2=2πfz2,fz2为第2零点对应的频率;P1=2πf1,f1为第1极点对应的频率;P2=2πf2,f2为第2极点对应的频率。根据上述传递函数,利用双线性变换(Tustin变换)和Z变换可以实现其离散化推导计算:

2.2 自适应型3P3Z1CZ闭环控制算法设计
3P3Z1CZ补偿器结构中的Qz等参数仅与锂电池充放电系统主电路的参数有关,即由输出电感、输出电容、电容ESR、输出电阻以及线路等效电感等参数决定。f1、f2仅与锂电池充放电系统中数字电源箱控制系统的计算周期相关,而KDC、frz则与控制系统的动态响应性能相关。为了实现电流域范围内的动态响应性能最优控制,需要完成对KDC、frz的在线自适应调整。同时,由于frz对于系统的整体响应敏感度较低,因此本文以KDC为研究对象,设计了多段式自适应3P3Z1CZ补偿器闭环控制算法。根据锂电池充放电系统的设计要求,获取所需电流期望值的范围,然后在所需范围内选取典型的期望值,根据理论推导和实验结果获取对应的最优KDC,然后对KDC进行多段式线性拟合。算法处理过程如图2所示。
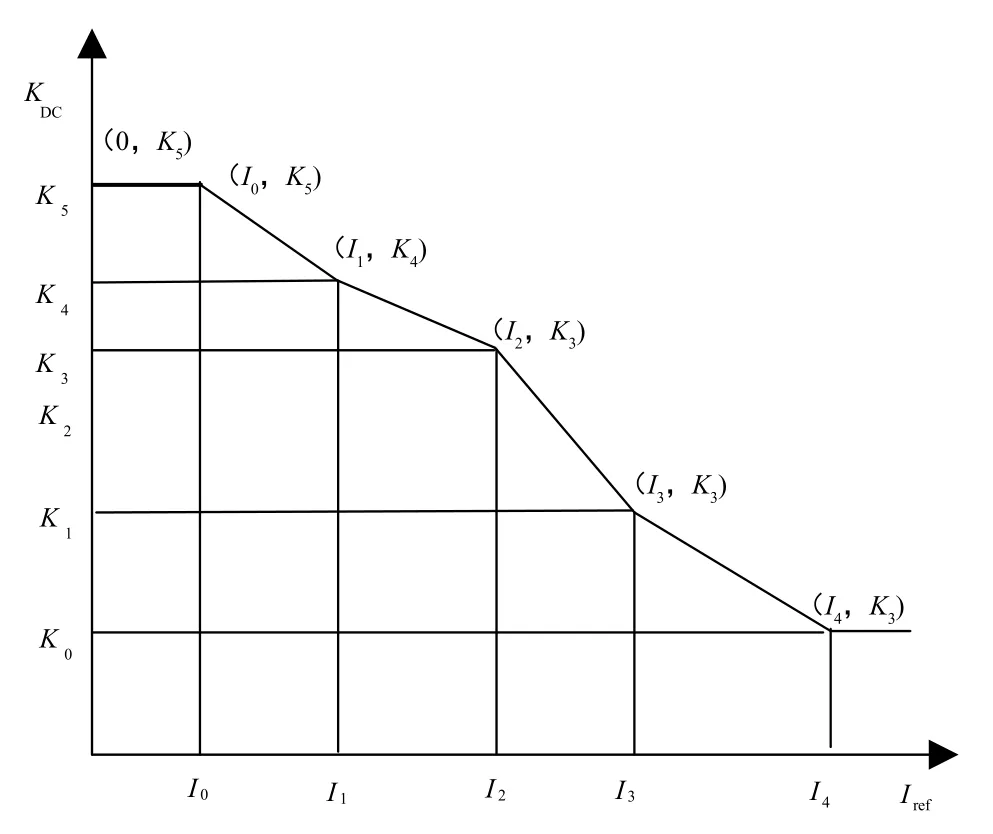
图2 多段式自适应算法处理过程
多段式线性拟合公式为:

将式(9)计算得到的KDC代入式(8),实现3P3Z1CZ闭环控制器参数的自适应处理,进而完成全电流域的最优动态控制。
3 仿真验证
在MathCAD中建立了双向Buck变换电路的数学模型,并对其进行仿真分析。电路主要的参数包括:输入电压Uin=14 V,输出电感L=22 μH,输出电阻Rout=10 mΩ,输出电容Cout=1 000 μF,电容的等效电阻Resr=10 mΩ,线路电感LLine=2.8 μH,线路电阻RLine=2 mΩ。电路幅值增益-频率和相位-频率响应曲线如图3所示。

图3 电路幅值增益-频率和相位-频率响应曲线
在研究上述电路特性的基础上,对3P3Z1CZ补偿器进行设计,分析其幅值和相位频率响应曲线。补偿器的相关参数包括:增益参数KDC=30,双极点频率frz=2 500 Hz,品质因数Qz=10 mΩ,第2零点频率fz2=1 000 Hz,第1极点频率f1=20 kHz,第2极点频率f2=20 kHz。3P3Z1CZ补偿器幅值增益-频率和相位-频率响应曲线如图4所示。
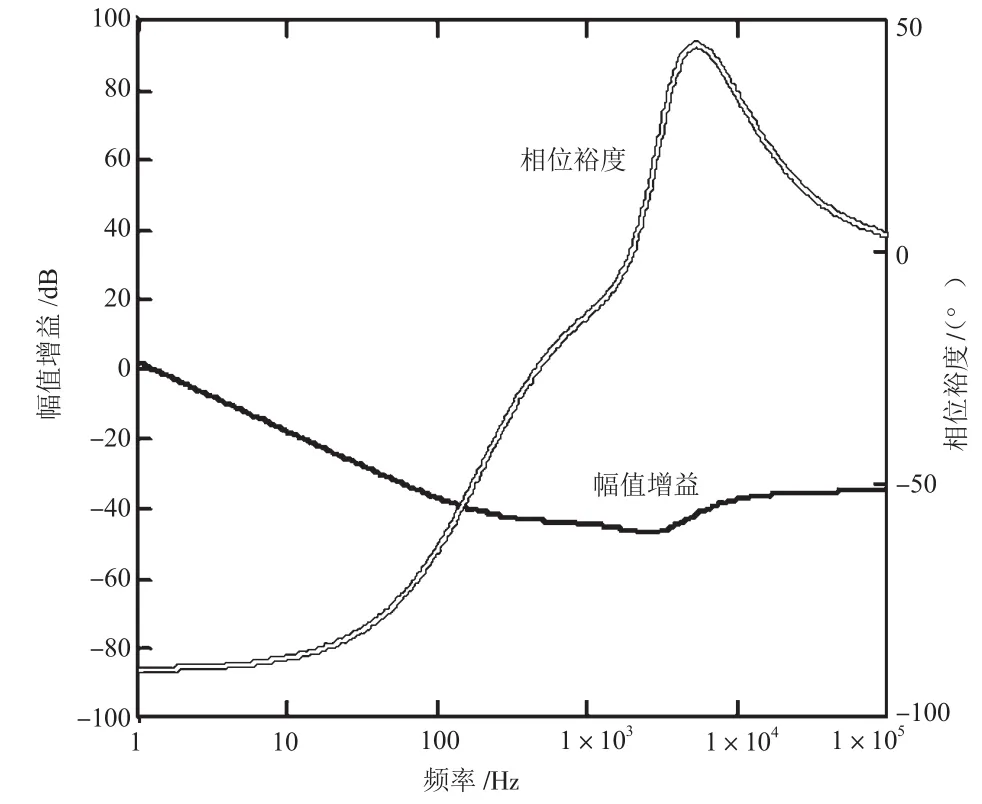
图4 3P3Z1CZ补偿器幅值增益-频率和相位-频率响应曲线
将电路的数学模型与补偿器的数学模型进行组合计算,获取准确的锂电池充放电控制分析模型,并对其阶跃响应的相关性能进行研究,分析其暂态性能和稳态性能。其对阶跃信号具有较好的系统跟随性能和稳态抗干扰能力,初步验证了相关控制算法的可行性和有效性。
4 实验分析验证
4.1 实验平台搭建
搭建完善的锂电池充放电实验平台,如图5所示。在此实验平台上进行大量锂电池恒流充放电实验,以测试系统的动态响应性能和稳态精度等核心指标。

图5 锂电池充放电系统实验平台
4.2 恒流充电和恒流放电实验
10 A充电电流启动瞬态波形如图6所示,在期望值为10 A的情况下,其充电响应时间为1.005 ms。10 A放电电流启动瞬态波形如图7所示,在期望值为10 A的情况下,可以快速平稳的启动,其响应时间为1.043 ms。

图6 10 A充电电流启动瞬态波形

图7 10 A放电电流启动瞬态波形
由上述实验可知,在全流域范围内,充放电的响应时间均在2 ms以内。对系统充放电的稳态精度进行测试,结果如表1所示。

表1 精度测试实验数据(单位:A)
根据表1,在全流域范围内,充放电的稳态精度均在0.02%以内。
5 结 论
针对锂电池的充放电特性进行分析,提出了一种基于自适应零极点补偿的锂电池充放电算法,可以使其在全电流域内的动态响应时间保持在2 ms以内,稳态精度在0.02%,提升了全电流域范围内充放电的动态响应性能和稳态精度。
