基于虚拟惯性频率调节的VSC-MTDC 系统自适应下垂控制策略

2022-08-17刘英培石金鹏梁海平杨博超

可再生能源 2022年8期

刘英培，石金鹏，梁海平，杨博超

（华北电力大学电气与电子工程学院，河北保定 071003）

0 引言

为应对化石能源引起的能源危机和环境污染问题，可再生能源发电受到了广泛的关注与应用[1]，[2]。基于VSC-MTDC 输电系统其具有高灵活性、稳定性、高扩展性等特点，是实现可再生能源发电并网、大规模新能源发电远距离输送的有效手段[3]。

随着电网中电力电子设备比例逐渐提高，电力系统的整体惯性有所降低，导致弱电网在扰动下频率会发生较大波动[4]， VSC-MTDC 输电系统采用主从控制、直流电压裕度控制和直流电压下垂控制时，无法实现频率调节[5]，[6]，而采用传统附加频率控制时，由于下垂系数固定，容易引起较大的直流电压变化。针对VSC-MTDC 系统参与交流电网频率调节，许多学者开展了相关研究。文献[7]，[8]通过测量不同换流器之间的频率实现对功率的精确分配进而调节直流电压和频率，但该方法须要通信支持。文献[9]，[10]提出了一种频率下垂与电压下垂结合的附加频率控制策略。该控制策略不需要通信即可提高电网的频率响应能力，但并未考虑下垂参数对直流电压的影响。文献[11]考虑下垂参数的影响提出了非线性电压、频率下垂控制方案，实现了频率调节和直流电压稳定，但并未考虑多端换流器协调。文献[12]提出了一种计及换流器间误差的调频控制策略。该控制策略兼顾了直流电压和频率的稳定，但在直流电压处于限时运行区时，牺牲了频率质量。文献[13]，[14]分析了惯性对频率的支撑作用，并提出了一种分散虚拟惯性控制方法。该方法利用直流侧电容模拟同步发电机为交流电网频率提供惯性支撑。文献[15]将虚拟惯性控制方法应用在两端柔性直流输电中，实现了柔直系统参与交流系统频率调节。文献[16]将虚拟惯性控制应用在多端柔直输电系统中，并考虑了虚拟惯性系数选取对系统直流电压的影响。

本文考虑VSC-MTDC 系统参与弱电网频率调节过程中的直流电压稳定问题，首先利用虚拟惯性频率调节将交流侧频率与直流侧电压参考值进行耦合，使直流系统为电网频率提供惯性支撑；其次，提出考虑直流电压偏差与换流器调节裕度的自适应下垂控制策略，并阐述了基于虚拟惯性频率调节的VSC-MTDC 系统自适应下垂控制策略实现电网调频的原理；最后，基于PSCAD/EMTDC 仿真平台验证了所提控制策略的有效性。

1 VSC-MTDC 系统结构及数学模型

由于风力发电场分布比较分散，利用VSCMTDC 系统可以实现多个风力发电场向多个受端系统供电。该系统能协调控制各个换流器之间的功率实现供电稳定性。

四端VSC-MTDC 系统结构如图1 所示。风力发电场S1，S2 经送端换流器VSC1 和VSC2 输入至直流网络，然后通过受端换流器VSC3，VSC4送至受端弱交流电网S3，S4。图中：Pi（i=1，2，3，4）为换流器发出的有功功率；B1，B2 为直流母线；Li为交流侧负荷。

图1 VSC-MTDC 系统结构图Fig.1 Structure diagram of VSC-MTDC transmission system

VSC 系统结构如图2 所示。

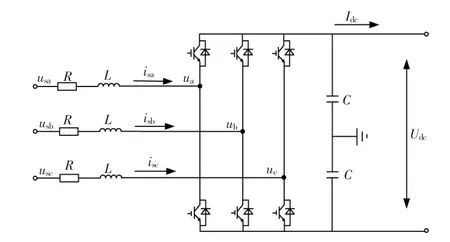
图2 VSC 结构图Fig.2 VSC structure diagram

图中：usa，usb，usc分别为网侧三相交流电压；isa，isb，isc分别为换流器三相交流电流；ua，ub，uc分别为换流器侧电压；C 为换流器直流侧电容；R 为换流器电阻；L 为换流器电感；Idc为直流电流；Udc为直流电压。式中：usd，usq，ud，uq，isd，isq分别为网侧交流电压、换流器交流电压、交流电流的d，q 轴分量；ω 为电网电压矢量的旋转角速度。

2 传统附加频率控制策略

传统附加频率控制策略如图3 所示。图中：Δf 为频率偏差；Pref为有功功率参考值；P 为有功功率实测值；Udc0为直流电压额定值；Udc为直流电压；K1为频率下垂系数；K2为直流电压下垂系数；idref为有功电流参考值；idmax，idmin分别为输出电流的上、下限值。

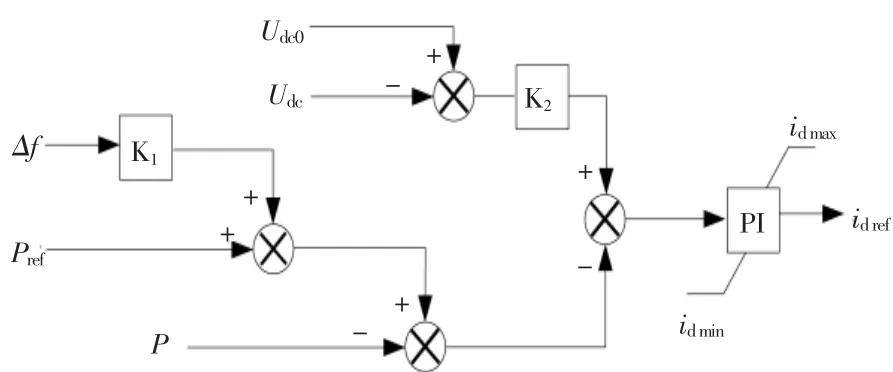
图3 传统附加频率控制原理Fig.3 Schematic diagram of traditional additional frequency control

该控制方案将频率偏差乘以系数K1叠加至有功功率参考值，在交流侧系统频率发生波动时，VSC-MTDC 系统能够依据频率变化动态调整有功功率参考值，进而改变有功功率；然后将频率下垂与电压下垂结合，在无通信的情况下实现VSC-MTDC 系统参与交流电网的频率调整。

传统附加频率控制中，直流电压下垂系数K2和频率下垂系数K1固定不变。若K1取值过大，较小的频率偏差会引起较大的功率波动，进而造成较大的直流电压偏差，严重时会导致直流电压越限，危害系统安全稳定运行。若K1取值过小，有功功率对频率偏差不敏感，影响频率调节效果。当K2取值过大时，较小的直流电压偏差也会引起较大的有功功率变化，严重情况下会造成换流器过载。当K2取值过小时，较大的直流电压偏差，只能引起较小的功率变化，影响直流电压的调节。为避免频率调节过程中下垂系数固定对直流电压调节的影响，本文提出一种基于虚拟惯性频率调节的VSC-MTDC 系统自适应下垂控制策略。

3 基于虚拟惯性频率调节的自适应下垂控制策略

3.1 虚拟惯性频率调节控制

传统电力系统惯性由同步发电机转子中储存的能量提供，同步发电机储存能量Es为

对比式（3），（4），可考虑利用VSC-MTDC 中VSC 换流器电容的能量，模拟同步发电机的特性，为系统提供惯性，如图4 所示[13]，[14]。

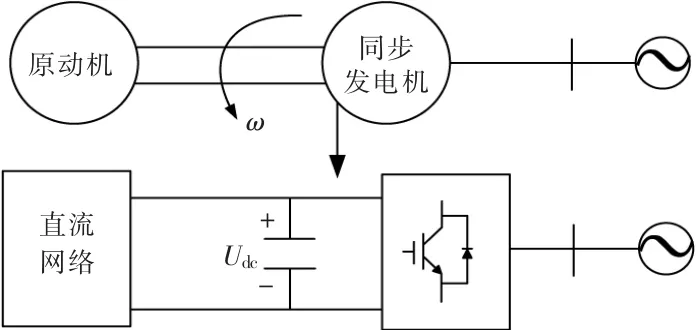
图4 换流器与同步发电机对比Fig.4 Comparison of inverter and synchronous generator

设VSC 换流器虚拟惯性系数为HVSC，建立发电机转子运动方程与VSC 直流侧电容充、放电方程之间的关系[17]，[18]。

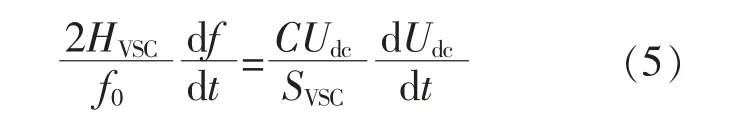
式中：f0为额定频率；f 为频率；C 为换流器直流侧

Udc0为200 kV、直流侧电容为750 μF、频率最大偏差为±0.5 Hz，虚拟惯性系数HVSC为0～10 s时，直流电压参考值Udcref与虚拟惯性系数HVSC和频率f 之间的关系如图5 所示。

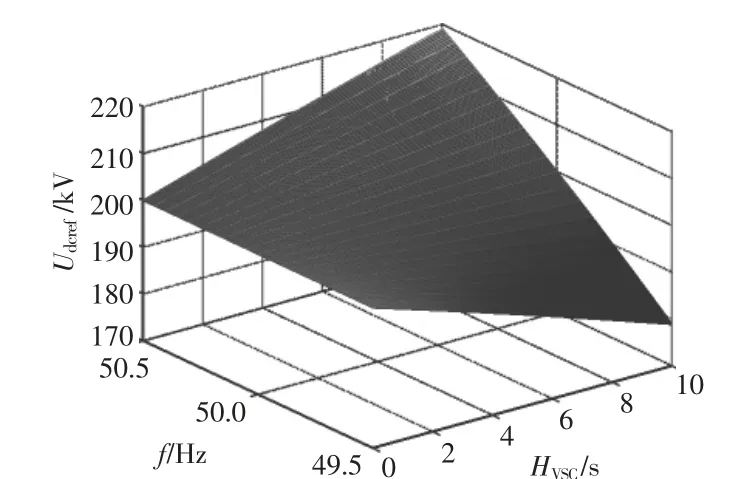
图5 Udcref-f-HVSC 关系曲面Fig.5 Udcref-f-HVSC relation surface

由图5 可得，当虚拟惯性系数固定不变时，随着频率偏差的变化，直流电压参考值动态调整，进而实现VSC-MTDC 系统参与交流侧频率调节。此外，虚拟惯性系数的大小会影响直流电压参考值的取值。

3.2 自适应下垂控制

式中：Udcmin，Udcmax分别为系统运行允许的直流电压偏差的下限、上限。

考虑功率调节裕度时VSC 换流器的P-U 下垂系数K 为

根据式（13）可以得出VSC 换流器Udc-P 下垂关系曲线，如图6 所示。

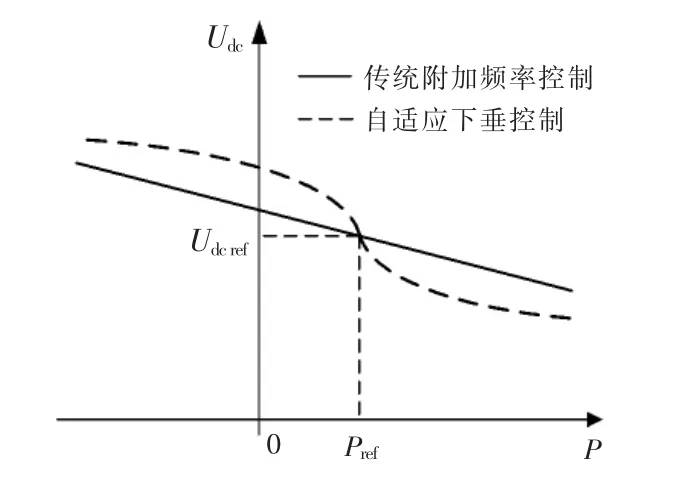
图6 Udc-P 下垂关系曲线Fig.6 Udc-P droop curve

由图6 可知，在VSC-MTDC 系统发生功率不平衡事件后，当直流电压在参考值附近时，直流电压快速变化实现系统的有功功率调节；当直流电压偏差较大时，降低直流电压变化率，直流电压变化速度减慢，避免直流电压越限影响系统运行安全。

将式（6）代入式（13），可得到基于虚拟惯性频率调节的自适应下垂控制表达式为

式（14）建立了有功功率P、直流电压Udc及频率f 三者之间的耦合关系，当交流侧发生扰动后，换流器发生有功功率不平衡，交流电网频率和直流电压产生偏差。根据式（6）可知，直流电压参考值会随着频率变化而变化，进而调节直流电压，根据式（14），在自适应下垂控制作用下，有功功率能够依据直流电压和频率的变化，实现实时调整。

当Udc0为200 kV、直流侧电容为750 μF、虚拟惯性系数HVSC 为3 s 时，可得到有功功率P、频率f、直流电压Udc三者之间的关系，如图7 所示。

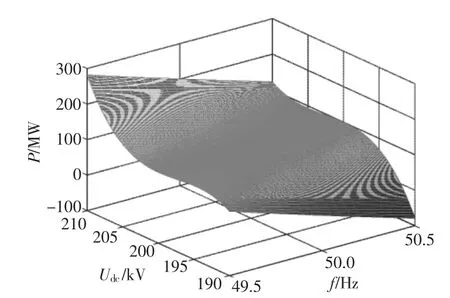
图7 P-f-Udc 关系曲面Fig.7 P-f-Udc relation surface

由图7 可知，当频率偏差和直流电压偏差较小时，此时有功功率变化量不大。随着频率偏差和直流电压偏差的增大，换流器输送的有功功率变化量增大，用以减小直流电压和交流侧频率的波动幅度。

基于虚拟惯性频率调节的自适应下垂控制策略如图8 所示。

图8 基于虚拟惯性频率调节的自适应下垂控制原理Fig.8 Schematic diagram of adaptive droop control based on virtual inertia frequency adjustment

4 仿真结果分析

为验证所提出控制策略的有效性，基于PSCAD/EMTDC 电磁暂态仿真平台建立了如图1的四端柔性直流输电系统仿真模型。其中VSC1，VSC2 采用定有功功率控制；VSC3，VSC4 分别连接弱电网并采用本文所提出的控制策略。系统的主要参数如表1 所示。

表1 4 端VSC-MTDC 系统主参数Table 1 Main parameters of four terminal VSC-MTDC network

续表1

本文选取虚拟惯性系数为3 s。为减少稳态时频率的较小波动引起控制器的频繁动作，设置频率阈值为0.05 Hz。直流电压允许最大偏差为±5%。

4.1 交流电网负荷减少

在t=22 s 时，交流电网4 负荷减少80 MW，在本文提出的自适应下垂控制策略和传统附加频率控制策略下的受端交流电网S3，S4 的频率、下垂系数以及直流电压的变化曲线如图9 所示。

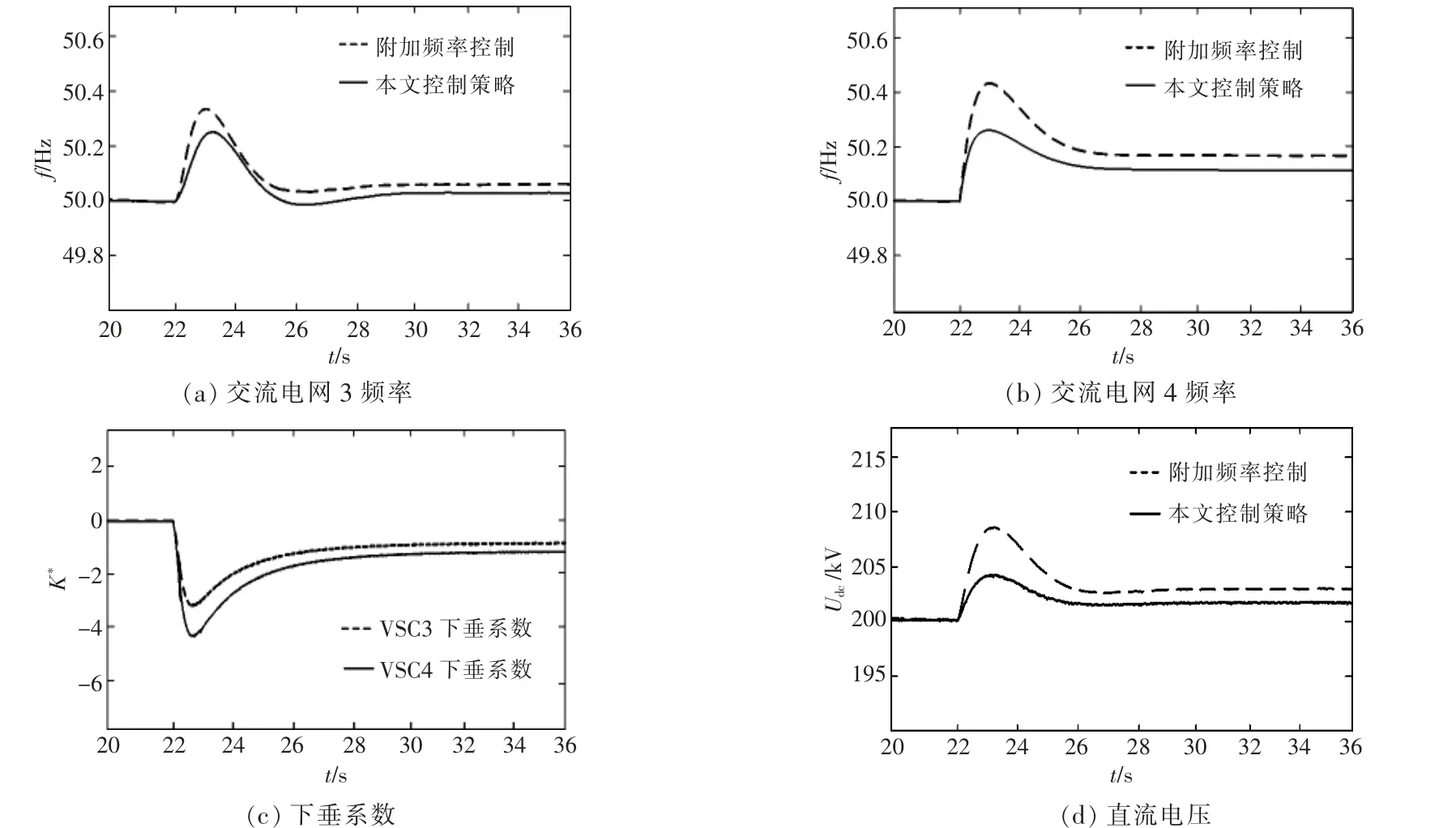
图9 负荷减少系统仿真结果Fig.9 Simulation results of load reduction

由图9 可知，当负荷减少后，受端系统频率上升。采用传统附加频率控制策略时，弱交流电网3和弱交流电网4 的波动幅值分别为0.38，0.41 Hz，两者频率波动幅值分别为0.22，0.23 Hz，显著降低频率偏差。在t=22 s 时，由于自适应下垂控制的作用，本文控制策略的下垂系数随着直流电压偏差的增大逐渐增大，定直流电压占据主要地位，直流电压波动幅值仅为4 kV。采用传统附加频率控制时，由于下垂系数固定，直流电压波动幅值达到了9 kV。因此，与传统附加频率控制相比，采用本文控制策略的直流电压离限值较远，直流电压质量得到了显著改善。

4.2 交流电网负荷增加

t=22 s 时，交流电网4 负荷增加80 MW。本文控制策略与传统附加频率控制策略下的仿真结果如图10 所示。

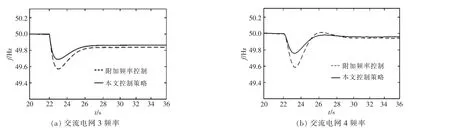
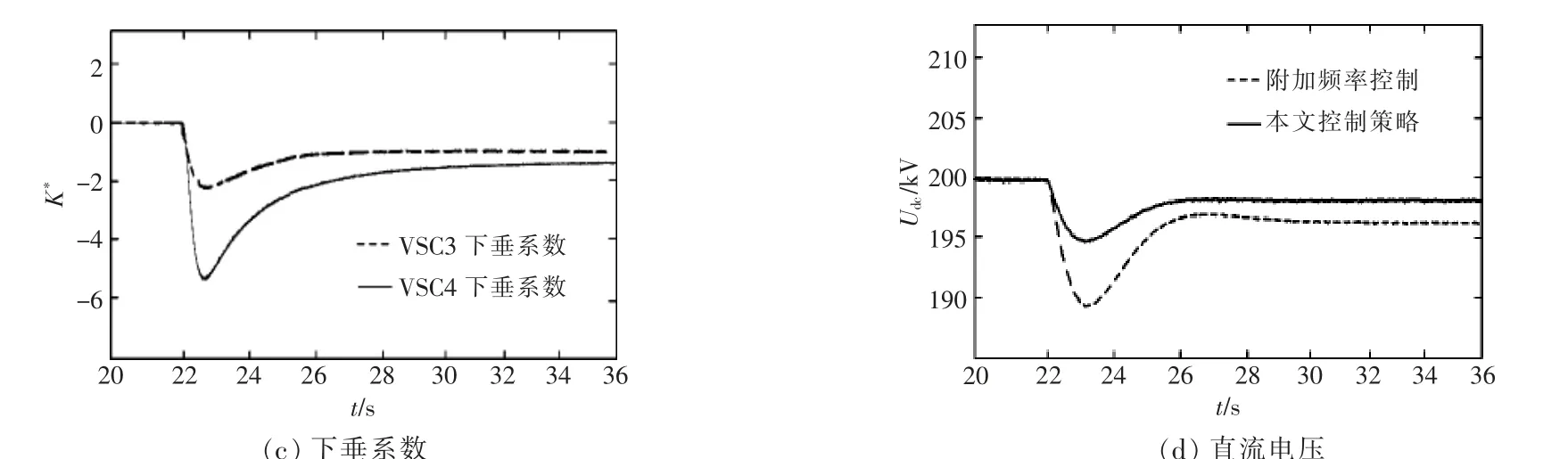
图10 负荷增加系统仿真结果Fig.10 Simulation results of load increase

由图10 可知，负荷增加后系统频率下降，传统附加频率控制下弱交流系统频率超调较大，交流电网3 和交流电网4 的最大频率偏差分别为0.42，0.4 H。采用本文控制策略时，两者最大频率偏差分别为0.3，0.22 Hz，与传统附加频率控制相比频率波动幅度显著降低，有助于提高互联系统的频率稳定性。采用本文控制策略时，下垂系数随着电压偏差的变化而变化，当频率偏差增大时，下垂系数增大，用以减小直流电压偏差。采用传统附加频率控制策略时，最大电压偏差为11 kV，超过直流电压偏差限值，而采用本文控制策略时，直流电压最大偏差降低为5.1 kV。因此，采用本文控制策略可以明显降低频率调节过程中的直流电压偏差，有利于VSC-MTDC 系统的运行安全。

4.3 交流电网发生瞬时短路故障

交流电网4 在t=22 s 发生持续时间为0.1 s的三相短路故障，采用传统附加频率控制和采用本文控制策略的仿真结果如图11 所示。

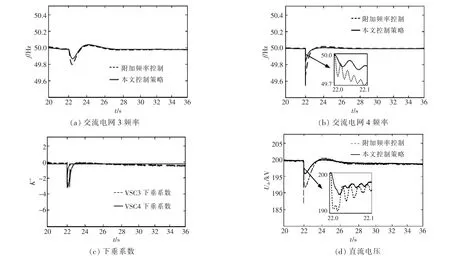
图11 电网瞬时短路故障Fig.11 Instantaneous short-circuit fault of power grid

由图11 可知，交流电网4 发生故障后，电网频率发生瞬时性跌落，之后频率逐渐恢复额定值。与传统附加频率控制策略相比，采用本文控制策略频率跌落速度减缓，幅值显著减小，恢复速度加快。采用传统附加频率控制时，由于其电压下垂系数固定，导致直流电压偏差较大，达到10 kV。在本文控制策略下，下垂控制系数随着直流电压跌落而增大，直流电压下降速度减缓，显著减小了直流电压跌落幅值，有利于直流电压恢复。采用本文控制策略时，可在一定程度上减小瞬时性故障下的直流电压和频率偏差，有利于故障恢复过程中直流电压和频率的稳定，防止直流电压和频率偏差过大，保证系统稳定运行。