水下永磁同步电机定子匝间短路电磁振动分析

张津铭，夏加宽

水下永磁同步电机定子匝间短路电磁振动分析

张津铭，夏加宽

（沈阳工业大学，沈阳 110870）

电机的径向电磁力是产生电磁振动的主要原因。本文从应力方程出发，推导了永磁同步电机气隙磁通密度和磁场产生的径向力波的表达式。以一台8极48槽水下永磁同步电机为例，对正常工况下的电磁模型进行空载有限元的仿真和电磁振动的加速度分析，将正常工况下仿真与实验二者的电磁振动加速度结果进行对比，验证了其仿真结果的正确性。之后对不同匝间短路故障程度下的电磁模型进行有限元的仿真及电磁振动的加速度分析，对比不同匝间短路程度的仿真数据，得到其匝间短路故障特征量。

永磁同步电机 匝间短路 电磁振动 振动加速度

0 引言

永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）与传统电机不同，励磁是由永磁体提供，其结构简单，运行可靠，效率高，功率密度高，性能好和噪声小，正是由于永磁电机的这些优点在现代船舶中被广泛应用[1, 2]。水下电机的运行会被很多的环境因素干扰，如振动、湿度等，极其可能出现电机的各种故障[3]。匝间短路故障在永磁电机的所有故障中是最常见的故障之一，而且它对于电机的损毁性非常的大。如果发生了匝间短路，但没有对其采取措施，这个故障就可能会发展成更为严重的故障[4, 5]，使电机不能够维持正常的功能，还有可能会损坏电机。

目前已有较多关于匝间短路的研究。文献[6]是通过励磁机励磁电流来判断匝间短路故障。文献[7]通过负序电流检测定子的故障。文献[8]分析了带有零序电压的匝间短路故障。文献[9]通过EMD定子电流分析短路故障。文献[10]是通过对称分量法检测到的负序阻抗，来判断是否发生了故障。

就目前的研究来看，故障的检测方法多集中与电流电压方面，对于振动方面的检测方法却少有报道。现有的对于振动方面研究多集中于电机正常运行工况，定子铁心位于气隙磁场之中，当电机运行时，其内表面将受到一个较大的径向电磁力，这就是产生振动的主要原因[11]。当电机发生严重的匝间短路故障，其定子铁心将受到高于正常运行时几倍的电磁力，从而促使电机发生剧烈的振动[12]。因此分析永磁同步电机在故障下产生的电机电磁振动特性，将可以在现有检测方法的基础上，更加多方面的了解匝间短路对永磁电机运行特性所产生的影响。

本文以一台8极48槽永磁同步电机为研究对象，推导了永磁同步电机气隙磁通密度和磁场产生的径向力波的表达式；通过正常运行空载工况仿真数据和实验的数据进行对比，验证其结果的正确性。对不同匝间短路故障程度下的电磁模型进行有限元的仿真，分析在故障运行下气隙磁密、电磁力、电磁振动等关键性能参数的变化，深入研究故障后永磁电机的运行状态，得到永磁同步电机匝间短路的故障特征量，为以后研究故障检测方法提供一定的理论支持。

1 永磁同步电机平面结构及主要参数

永磁同步电机平面结构如图1所示。此电机是一台8极48槽的永磁同步电机，其主要参数见表1，额定功率3 kw，额定电压380V，额定电流10.5 A，额定转速2500 r/min，槽数/极数48/8。

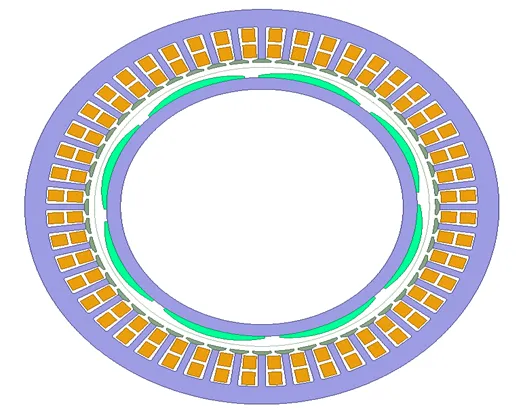
图1 水下永磁电机平面结构图

2 电机电磁力分析

2.1 永磁体磁动势计算

当永磁体单独作用时其产生的谐波次数可表示为

永磁体单独作用时气隙的等效磁动势为[13]

式中，F为次谐波磁动势幅值，A；为电流角频率，rad/s；为时间，s；为极对数；为机械角度，rad。

2.2 电枢磁动势计算

电枢反应产生的基波磁动势和次谐波磁动势分别为[14]

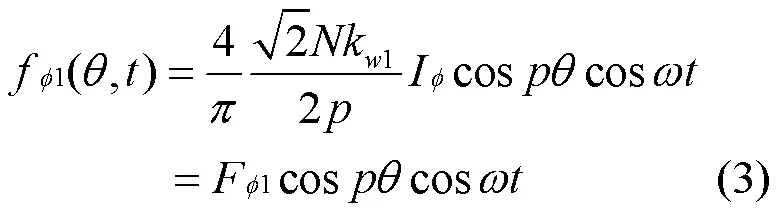
式中，为每相串联匝数，I为电流有效值，k为绕组系数。

定子三相对称电流合成磁势又可以表示为

其中

2.3 气隙磁导计算

等效气隙磁导为[14]

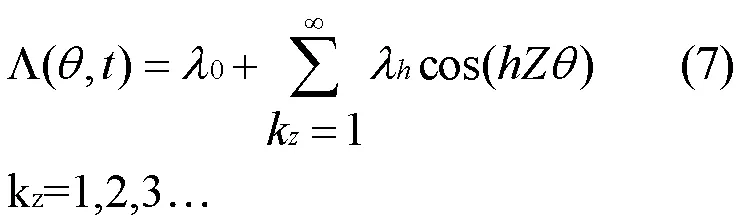
式中，λ为气隙平均磁导，H–1；为齿谐波阶数；λ为气隙阶齿谐波磁导幅值，H–1。

2.4 气隙磁密计算

将式（2）作用于式（7）等效磁导上，永磁体产生的气隙磁密为

将式（5）作用于式（7）的等效磁导上，电枢产生的气隙磁密为

2.5 电机径向电磁力的计算

定子受到径向电磁力f(N/m2)为

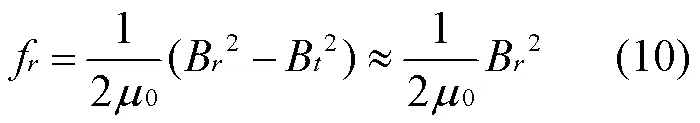
式中B为磁密的径向分量，T；B为磁密的切向分量，T；μ为真空磁导率，μ=4π×10-7H/m。

由于气隙磁密的径向远远大于切向，所以计算时只考虑径向，而不考虑切向。将前文所求永磁体产生的气隙磁密和电枢产生的气隙磁密都视为径向分量时，其径向电磁力的表达式为[15]。

式中，第1项为永磁体作用时产生的径向电磁力、第2项为电枢作用时产生的径向电磁力，第3项为永磁体与三项对称电流共同作用时产生的径向电磁力。

3 电机正常运行时空载磁密、电磁力有限元分析

采用8极48槽的二维平面有限元电机模型，以定转子间气隙某一位置的圆为观察路径。在电机未发生匝间短路故障时，对其进行有限元仿真，径向气隙磁密及其傅里叶分解结果如图2所示，径向电磁力及其傅里叶分解结果如图3所示。

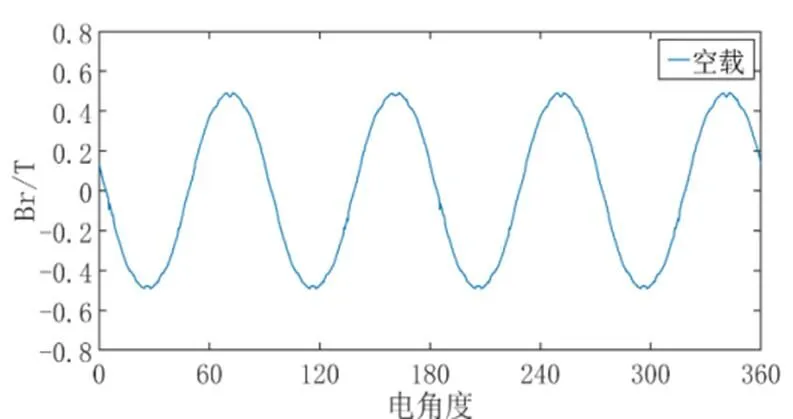
图2显示了电机径向气隙磁通密度的空间分布，由于空载时气隙磁场受电枢磁场产生的磁动势影响较小，因此定子槽口位置的波峰和波谷波动较小。

谐波分析结果表明，上述的气隙磁密，电磁力及其相应的傅里叶分解，气隙磁密的谐波次数为4，12，28次等，电磁力的谐波次数为8，16，24次等，由于本次采用的电机极对数为4，对于一对极下的气隙磁密和电磁力谐波次数都应除以4，所以一对极下气隙磁密的主要谐波次数为1，3，7次等，电磁力的主要谐波次数为2，4，6次等，其中基波幅值在所有的谐波次数里是最大的。

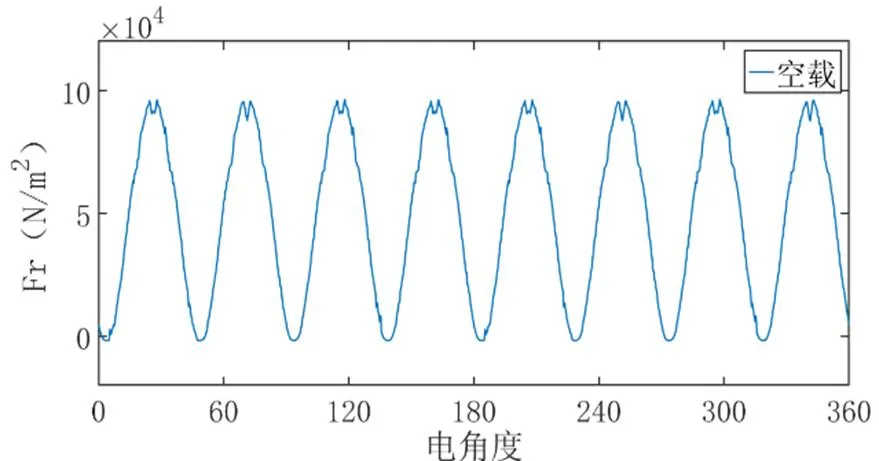
由图3可知，径向电磁力密度空间分布波形随空间位置呈周期性变化，且相对于峰值呈轴对称。

正常未发生故障下，电机也会发生一定程度的振动，为了研究匝间短路下的振动情况找出振动的频率点，分析了电机在转速为1500 r/min时电磁振动加速度仿真。以定子外圆作为观察点，得到电机正常运行时空载电磁振动有限元仿真的谐波响应，如图4所示。

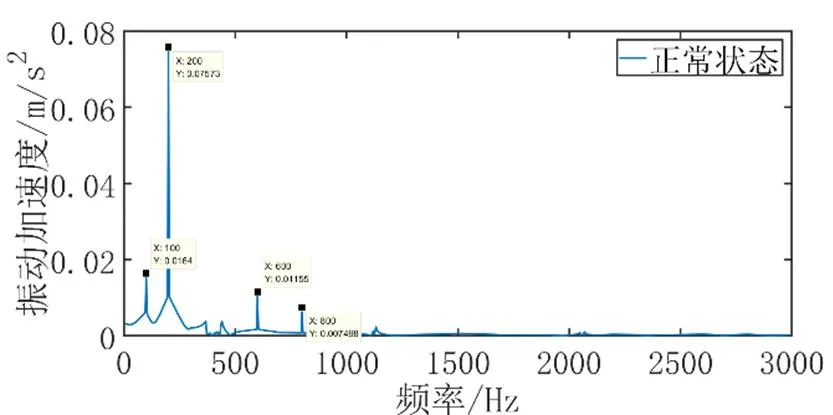
图4 永磁同步电机振动加速度仿真结果

由图4可见，频率分别为100 Hz、200 Hz和600 Hz时，振动加速度的幅值在图中表现的较为明显。从径向电磁力分量可以看出，当振点频率为基频的2倍即200 Hz时，振动加速度的幅值最大，而且当频率为100 Hz（基频）和600 Hz（6倍频）的振动加速度幅值相对于其他的频率点也是较大的，因此，在基频，2倍频和6倍频下，电机将发生较大的振动。

将本次的实验电机连接上振动测试仪，将测试仪的传感器放置在外壳的径向方向上，如图5所示。当电机以1500 r/min稳定运行时，记录下此时电机振动的数据及波形，得到实验测得的电机振动加速度，如图6所示。

图5 永磁同步电机振动加速度实验图

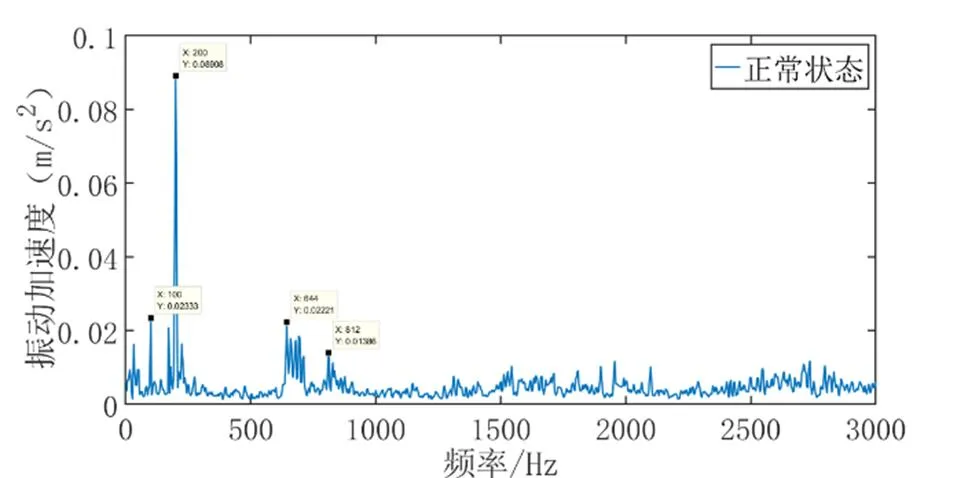
图6 永磁同步电机振动加速度实验结果

从图4与图6对比中看出，在振动仿真图中幅值较大的点为100 Hz、200 Hz、600 Hz处，在振动实验图中幅值较大的点为100 Hz、200 Hz、644 Hz，二者结果基本一致，虽然实验测量得到的数据与有限元的数据存在着偏差，但表现出振动幅值与振动频率点的分布规律一致，证明了有限元电磁仿真的正确性。

在对比的结果中，我们能够看到图6中振点的振幅普遍略大于图5中有限元的仿真结果，而且实际的测量中也会有一些有限元仿真中没有的频率点，这时由于除径向电磁力外，其他的因素所导致的电机发生了振动，这些振动并非由径向电磁力引起的，而且相比于100 Hz、200 Hz时其振点的振动幅值并不大，故不对其加以研究。

4 电机匝间短路时径向磁密、电磁力有限元分析

在未发生故障时，已经对其振动响应进行了有限元分析及实验分析，分析可知在发生匝间短路后，磁场将发生畸变，电磁力幅值也将发生一定程度的增大，从而引发电机的径向电磁振动。

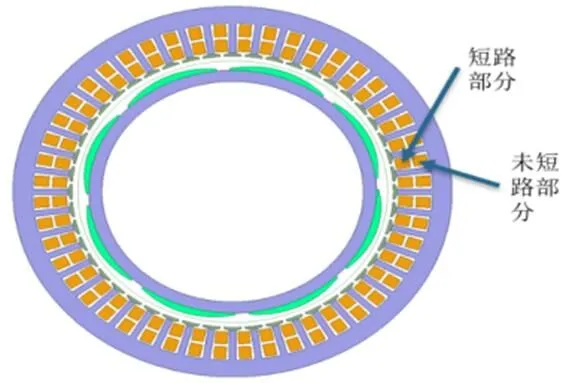
图7 永磁同步电机短路匝位置

有限元分析中设置的短路情况如图7所示，在每次仿真前都要改变每槽导体的绕组匝数，使其达到发生匝间短路的目的，每个槽匝数原为15匝。将同一个槽内分为匝间短路绕组和未发生匝间短路绕组。短路匝数设置为3匝和5匝。

为了便于观察，取一对极下的气隙磁密和电磁力曲线进行观察.

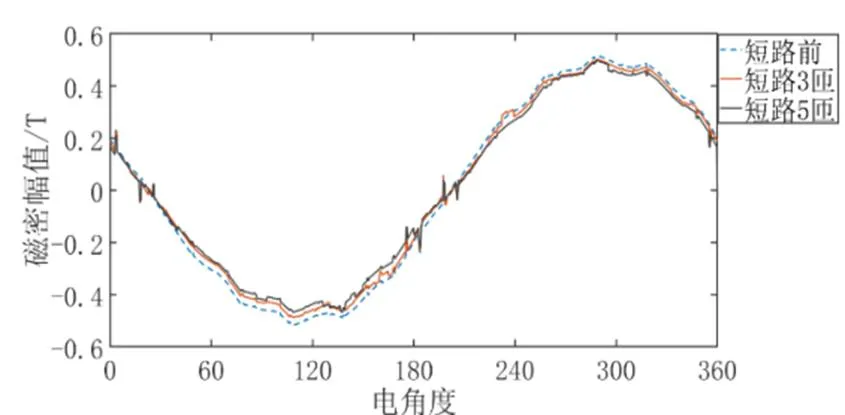
不同的短路程度下电机气隙磁密及傅里叶分解的有限元计算结果如图8所示。从图中可看出，在发生了不同程度的匝间短路后，电机的气隙磁密波形有一些较为明显的波动，气隙磁密傅里叶分解得到的谐波幅值随着短路匝数的增加而逐渐减小。

计算不同匝间短路程度下电机径向电磁力的有限元计结果如图9所示。由电磁力波形可以看出，随着短路匝数的增加，电磁力的幅值呈现较大程度的增加。由FFT分析结果可看出，2次谐波幅值，4次谐波，10次谐波和12次谐波有较明显增幅。

与前文振动分析类似，取正常运行和两次匝间短路的二维有限元分析得到了电机的径向电磁力，将其加到电机三维结构模型上。电机转速设置为1500 r/min，其有限元分析所得到的径向电磁振动结果如图10所示。

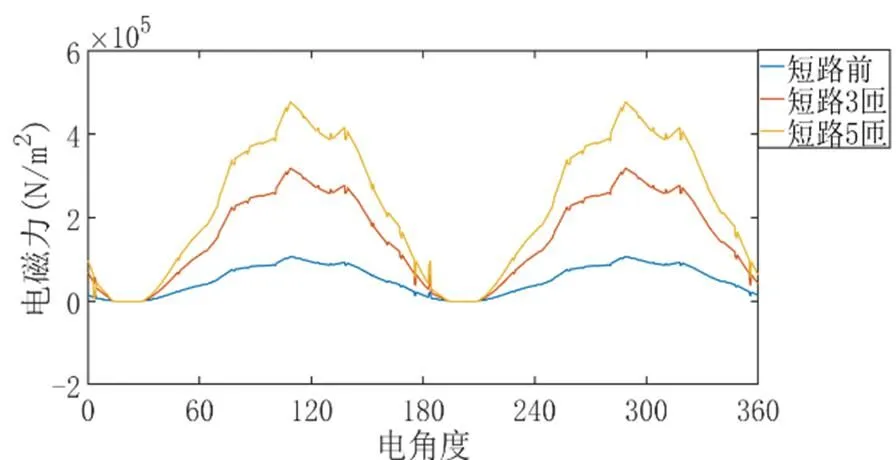
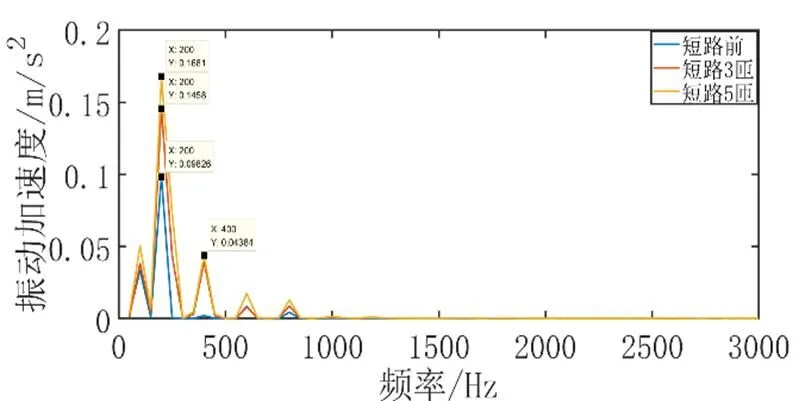
图10 永磁电机匝间短路故障振动加速度仿真结果

对比图10的波形可看出，在不同程度的匝间短路下，其振动的峰值非常清楚的可以看到比正常运行时大的多，反映出匝间短路会使得电磁力增大，其中不同的频率点呈现出不同的增长趋势。二倍频随着匝间短路的发生增大最明显，故此电机的低频段振动主要是由于二倍频引起的。在未发生匝间短路的情况下四倍频振动幅值并不明显，而在匝间短路故障下四倍频呈较大的增长趋势，所以四倍频的频率振点可以作为匝间短路的故障特征量。

5 结语

本文推导了永磁同步电机气隙磁通密度和磁场产生的径向力波的表达式。在未发生匝间短路故障下对一台水下永磁电机进行振动加速度的仿真，将仿真结果与实验测得电磁振动加速度结果进行对比，二者结果基本一致。在不同匝间短路故障程度下的电磁振动的谐响应分析中，得到二倍频是在低频率段产生振动的主要原因，无故障下四倍频幅值很小，而匝间短路故障下四倍频有明显的变化趋势，这一点可以为以后研究故障的检测方法提供一定的理论基础。

[1] 唐任远. 现代永磁电机理论与设计[M]. 北京: 机械出版社, 1997.

[2] 赵文峰. 浸水永磁同步电机振动噪声研究[D]. 北京: 中国舰船研究院, 2018.

[3] 孔汉. 永磁同步电机故障对电机综合物理场的影响机理研究. 西北工业大学, 2016.

[4] Li Liu, Cartes D. A. On-line Identification and Robust Fault Diagnosis for Nonlinear PMSMDrives Diagnosis for Nonlinear PMSM Drives[C].American Control Conference 2005, 2005(3): 2023-2027.

[5] Swarnakar S, Mukhopadhyay S, Kastha D. Fault Detection and Remedial Strategies forInter-Turn Short Circuit Faults in a Permanent Magnet Brushless DC Motor[C]. Indicon2005 Annual IEEE, 2005: 492-496.

[6] 方芳. 定子绕组匝间短路故障谐波传递特征[J]. 船电技术, 2011, 31(7): 3.

[7] 侯新国, 吴正国, 夏立等. 瞬时功率分解算法在感应电机定子故障诊断中的应用[J]. 中国电机工程学报, 2005, 25 (5): 110-115．

[8] Garcia. P, Briz, et al. Diagnostics of induction machines using the zero sequence voltage[C]. Industry Applications Conference, 2004. 39th IAS Annual Meeting. Conference Record of the 2004 IEEE, 2004: 735-742.

[9] J Rosero, L Romeral, J A Ortega, et al. Short Circuit Detectionby Means of Empirical Mode Decomposition and Wigner Ville Distribution for PMSM Running Under Dynamic Condition[J]. IEEE Transactions on Industrial Electronics, 2009, 56 (11): 4534-4547.

[10] Kohler J L,Sottile J, Trutt F C. Alternatives for assessing the electrical integrity of induction motors[J]. IEEE Transactions on Industry Applications, 2002, 28(5):1109-1117.

[11] 杨浩东. 永磁同步电机电磁振动分析[D]. 杭州: 浙江大学, 2011.

[12] 朱玉壁, 洪水盛. 平圩电厂1号发电机10号轴振动分析[J]. 中国电力, 2000, 33(10): 45-47．

[13] 王秀和,邢泽智,赵文良,等.表贴式永磁同步电机空载电磁激振力波的计算方法, CN111199124A[P]. 2020.

[14] 许实章. 电机学[M]. 北京: 机械出版社, 1981.

[15] 陈益广,韩柏然,沈勇环,等.永磁同步推进电机电磁振动分析[J].电工技术学报, 2017, 32(23):7.

Electromagnetic vibration analysis of stator inter turn short circuit of underwater permanent magnet synchronous motor

Zhang Jinming, Xia Jiakuan

(Shenyang University of Technology, Shenyang 110870, China)

TM341

A

1003-4862（2022）08-0043-05

2022-02-10

张津铭(1997-)，男，硕士。研究方向：电机及其控制。E-mail: 995185096@qq.com