基于概率统计的新型研发机构绩效评价测算方法

王梦婷,邓 媚

(广东省生产力促进中心,广东广州 510070)

0 引言

近年来,新型研发机构蓬勃发展,已成为我国区域创新体系的一支重要的生力军,是各地吸引高层次人才、知识、技术、资本等创新要素的重要牵引。作为聚焦科技创新需求的创新载体,新型研发机构主要从事科学研究、技术创新和研发服务,投资主体多元化、管理制度现代化、运行机制市场化、用人机制灵活化是其主要特色。在建设世界科技强国的新形势下,在促进产业链、创新链、资本链三链融合的迫切需求下,政府需要构建稳定权威、综合配套、精细协调的科技创新法治保障体系,对新型研发机构进行公平公正的绩效考核,以构建核心队伍稳定、人才流动顺畅、科教融合优质、成果转化高效及分配机制合理的现代治理体系,赋予创新主体更大的自主发展空间。

科技部印发的《关于促进新型研发机构发展的指导意见》中明确指出,科技部组织开展新型研发机构跟踪评价,地市政府组织开展绩效评价,根据评价结果给予新型研发机构相应支持。目前,不少省市的科技管理部门都建立了新型研发机构绩效评价制度,定期对新型研发机构进行绩效评价,并将评价结果作为后续政策、资金等支持的重要依据。例如,山东省以3年为1个评价周期,原则上每年度评价1次;河南省每两年对新型研发机构开展1次评价;广东省以3年为1个评价周期进行动态评估;四川省以两年为1个绩效评估周期;重庆市每3年进行1次考核;上海市、北京市等也在建立相应的评价机制。因此,持续对新型研发机构绩效评价的评价方法、评价流程进行研究和优化,对促进评价结果的公平、公正和我国新型研发机构的健康发展意义深远。

1 新型研发机构绩效评价研究现状

目前,关于新型研发机构绩效评价的研究主要集中于考核指标的确定,包括利用何种理论工具科学分析绩效影响因素、构建何种模型制定考核指标体系或确定指标权重。如周恩德等[1]通过层次回归分析法分析了新型研发机构创新绩效评价的影响因素;何帅等[2]通过结构方程模型对新型研发机构的绩效影响因素及作用机理进行了检验;孟溦等[3]基于资源依赖和社会影响力的双重视角,运用理论分析方法,根据新型研发机构所处的发展时期,建立了与之相适应的分类评价指标体系;郭百涛等[4]结合德尔菲法和网络层次分析法(ANP)进行实证研究,确定绩效评价的一级、二级、三级指标及其权重;王腮炜等[5]针对科技数据类的新型研发机构,从科技数据价值链形成和利益相关者合作两个维度出发,构建适用于建设期、运营期的绩效评价指标体系。

关于如何将各个指标测评出的数值与其权重联系起来计算指标实际得分,现有研究缺乏深入的研究和探讨。针对计分方式开展的研究主要提供了以下两种思路和方法:一是通过设定区间标准值对基础指标进行无量纲化处理,然后采用加权综合评测法得到被考核机构效用值[6];二是专家事先设定好得分区间,各指标所属的得分区间根据指标评测结果相对位置的百分比排序确定,之后由专家根据实际情况酌情给出具体的得分系数,最后采用加权综合评测法得到被考核机构的得分。这两种数据处理方法均简单易操作,但科学性、客观性不足。就第一种处理方法而言,由于无量纲化计算是基于事先设定好的标准区间,最终的考核结果与标准区间的设定也紧密相关,而标准区间设定的科学性和合理性则无从得知。第二种处理方法更加简单直观,仅需对各指标的实际考核结果进行排序,计算其所在的相对位置,对应到设定好的得分区间,专家即可根据实际情况给定最终的得分系数,但此做法的可靠性、稳健性得不到保证。

首先,得分区间及其对应的得分系数的设定标准很难通过科学的计算或推导得出,可能会存在区间设定不合理,导致两个指标结果十分接近的被考核机构落到两个不同的得分系数区间内,或使得两个指标结果相差甚远的被考核机构落到同一个得分系数区间,从而产生比实际差距大的得分差;其次,得分系数区间确定后,专家根据实际情况给定具体的得分系数时,可能出现由于个体差异导致的不客观、不公正,进而影响被考核机构的实际得分,造成考核结果的不可靠性。

综上所述,现有研究对评价指标的理论探讨较为深入和全面,但缺乏有关数据处理、评价方法等实证研究,新型研发机构评价结果有待使用更优化的统计方法进行计算[7]。因此,寻找一种科学合理、简单易操作的数据处理方法显得十分必要。本文基于最小二乘法,从概率统计的视角切入,重点研究新型研发机构绩效评价的数据统计方法,以期为新型研发机构的数据统计及计分方法提供更为科学的参考。

2 基于概率统计的新型研发机构绩效评价测算方法

在实际的新型研发机构绩效考核中,通常每家被考核单位的最终得分是由多项指标综合确定的,但是在指标体系设计时,考虑到考核的全面性、综合性,考核指标设置的数值可能有单位(如人次、万元等),也可能是无量纲数值,由于考核指标的单位不统一,在计算被考核机构所得总分时,无法直接相加求和。如何在指标计算实际结果与其权重之间建立科学的联系,既可对考核指标进行归一化,又能保留各指标的真实分布情况,从而进行得分换算,这是进行绩效评价测算的关键点,也是难点所在。

从考核实际情况来看,各考核指标中得分高与得分低的应为少数,多数被考核单位的同一个考核指标得分应集中在中间某一区间,即“两端少,中间多”,服从正态分布。

2.1 正态分布理论分析

正态分布是一种连续型随机变量的概率分布,呈现“两头小、中间大”的分布形态。将平均数为0、标准差为1的正态分布称为标准正态分布(标准正态分布曲线见图1)。

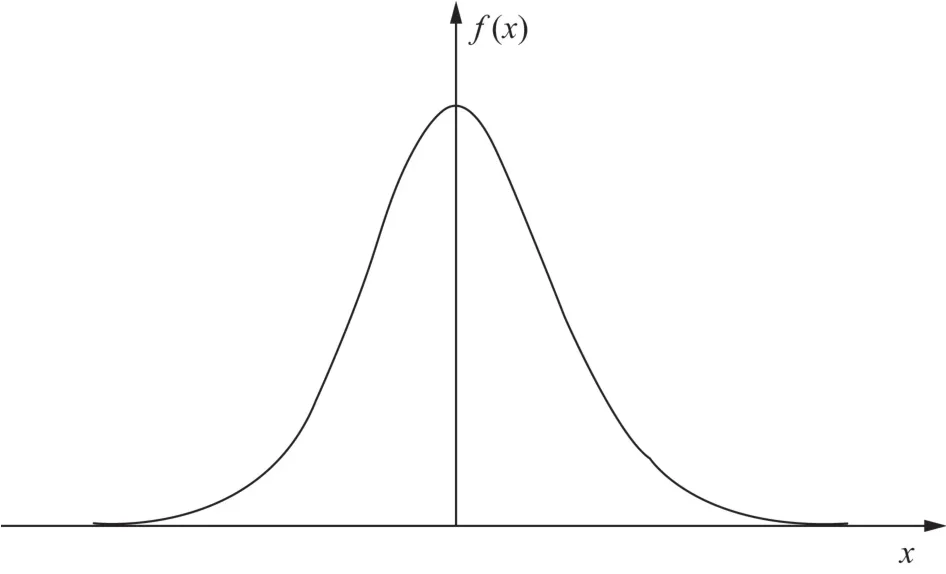
图1 标准正态分布概率密度示意

从图1可知,标准正态分布曲线具有以下特点:其一,曲线在X=0(即平均数)处为最高点;其二,曲线以X=0为轴,双侧对称;其三,曲线从最高点向左右缓慢下降,并无限延伸,最后接近基线,但永不与X轴相交;其四,标准正态分布上的平均数为0,标准差为1。

为了更直观地说明问题,引入分位数α。分位数指连续分布函数中的一个点,这个点对应概率p(见图2)。根据图2所示,α=0.5-p, 查标准正态分布分位数表即可得到标准正态分布下的Pα。根据样本S计算得到平均值μ和方差s2,那么根据公式M=Pα×s+μ,即可将标准正态分布映射到平均值为μ、方差为s2的正态分布。

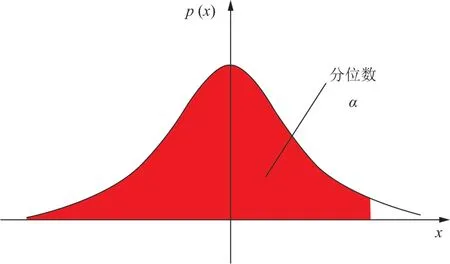
图2 概率分布的分位数示意

2.2 正态分布在绩效评价中的应用

在新型研发机构的绩效考核中,鉴于各考核指标的实际情况,无法统一量纲并直接进行得分计算,但可以根据考核要求通过多种方法,如多层次分析法、主成分分析法、专家打分法等确定各项指标i的权重wij(j为第j家被考核机构), 将被考核单位的某项指标测算值视为样本Si,则第j家被考核机构的第i个指标得分记为Sij。

绩效考核指标得分计算的问题转化为:对于样本Si,已知优秀率Ki,如何科学确定满分值Mi。当Si≥Mi时,得分系数为1;当Si＜Mi,得分系数为。通过计算,样本Si的带量纲数值巧妙地转换到了 0,1[ ]的得分系数之间,得分系数再乘以权重Wij,即为第j家被考核机构的第i个指标的最终得分。

2.2.1 科学、公平、公正地制定优秀值

对于任何一个被考核机构而言,一定会有一部分被考核机构能在某一考核指标得到优秀评价,如何制定考核指标的优秀值(即满分值),关乎到整个考核的科学与公平。本文通过引入正态分布理论,旨在科学地制定出优秀值。具体制定步骤为:

(1)根据实际工作需要,设定优秀率为K;

(2)根据优秀率K,可得α=0.5-K,查标准正态分布分位数表得到标准正态分布下的分位数Pα;

(3)计算被考核机构的各项考核指标的平均值μi和方差s2i;

(4)根据公式Mi=Pα×si+μi计算得到考核指标优秀值。

例如,某省设定80家被考核新型研发机构的优秀率为20%,此80家新型研发机构的某项考核指标,如科技成果登记数量的平均值为15项、标准差为3,根据正态分布理论计算科技成果登记数量的优秀值为:

(1)根据优秀率20%,得α=0.3,查标准正态分布分位数表得到标准正态分布下的分位数Pα为0.84;

(2)根据平均值15和标准差3,利用公式M=0.84×3+15计算得到优秀值为17.52分。

2.2.2 得分系数及实际得分的科学计算

根据正态分布理论,可得到各考核指标的优秀值,将各被考核机构的所有考核指标根据指标优秀值进行标准化,即将各考核指标统一为无度量单位的无量纲数值,作为该指标的得分系数。

(1)根据考核指标测算值Si和该指标优秀值Mi,由公式计算得分系数。

(2)将各考核指标得分系数乘以对应的指标权重Wij,得到各考核指标的实际得分。

例如,某被考核机构的科技成果登记数量为12项,则该被考核机构科技成果登记数量的得分系数为12/17.52=0.68。通过把各考核指标的原始数值转换为得分系数,不仅可比较被考核指标间的横向差距,还可看出同一被考核单位不同考核指标的实际情况,即该被考核单位的强项和弱项。

将各考核指标的得分系数与该考核指标的权重相乘,即为该项指标的实际得分。例如,若上述某被考核单位科技成果登记数量的指标权重为4,则该考核指标的实际得分为0.68×4=2.74分。通过此方法计算出被考核机构所有考核指标的实际得分,将各考核指标实际得分相加即可得出各被考核机构的考核总分。

3 概率模型在新型研发机构绩效评价中的应用

2020年,广东省某地市在新型研发机构绩效考核中创新性引入正态分布概率模型。此次绩效考核,一方面是为了帮助各新型研发机构发现自身优劣势,从而发挥自身资源禀赋,强化优势服务能力,有针对性地补齐劣势和短板,进一步明确发展方向和发展重点;另一方面有助于政府有关管理部门强化对新型研发机构的管理以及给予后续支持,进而通过奖优汰劣,深入实施新型研发机构提质增效计划,支撑地市科技创新发展。在考核要求中,最重要的是要能真实、客观地获得各被考核机构的实际得分,真实地反映出各机构之间的差距,突出新型研究机构发展中存在的问题。

考核采用机构自评与专家评议相结合的方法。首先,专家结合地市考核要求,根据新型研发机构的实际情况制定好考核指标及其对应的权重,由被考核机构对考核指标进行自评,并提供自评数值的测算依据。同时,根据正态分布原理及政府给定的20%优秀率,计算得出各考核指标的优秀值。其后,进入专家评议阶段,专家参考各指标的优秀值,对考核指标进行全面评估,确定各考核指标的最终优秀值。最后,计算得出各考核指标的得分系数,进而计算出各指标的实际得分及考核总分。

对整套绩效考核26项指标的得分情况进行分析,发现在26项考核指标中,仅有5项考核指标的优秀值由专家根据评议及现场考察情况,结合政府资金投入的产出预期等进行了向上微调整,其他21项考核指标的优秀值均得到了专家组的认可和使用。使用计分方法得出的被考核单位的排列位次及得分差距与被考核单位实际情况、专家判断和政府预期完全吻合,进一步证实了该创新性计分方法的科学性、精准性和客观性。

4 结语

新型研发机构的绩效考核是由指标体系建立、工具选择、权重设定、数据处理等多个过程组成,其中考核指标及其权重的设定是最关键的环节之一。目前,在绩效考核指标及其权重的设定方面已经有丰富的理论和实证研究,方法越来越科学,设定更加全面、完整,但对于指标及其权重确定后如何科学计算出得分尚未有较好的理论及做法,而这正是确保绩效考核公平、公正的前提和保障。本文通过将正态分布概率模型引入到绩效考核工作中,破解了目前通过事先设定标准区间或设定得分系数区间带来的主观性、不准确性、不科学性等问题,解决了难以精确反映各考核指标间、各被考核机构间实际差距的难题,为绩效考核计分工作提供了科学的理论依据,有利于以更科学的计分方式确保考核的真实性、公平性、公正性,为新型研发机构绩效考核工作提供了新的思路和方法。