基于ARMAS(p,q)退化冲击模型可靠性的预测
2022-08-16莫祯祥李艳君
张 权, 莫祯祥, 李艳君, 韩 旸
(齐齐哈尔大学 理学院,黑龙江 齐齐哈尔 161006)
0 引言
冲击模型中强度的预测[1]一文中已经给出了自回归强度冲击模型(Autoregressive Shock,简记为ARS(p))中冲击对将来影响的预测问题。这个问题的局限是模型仅与以前时刻的自身冲击有关,而文章具有随机扰动强度冲击模型的预测[2]一文中,又仅仅讨论了将来系统与以前进入系统的随机干扰存在一定关系。非常自然的考虑到一个问题,是否有这样的冲击系统,它不仅与以前时刻的自身值有关,而且还与以前进入系统的随机干扰存在一定关系?本文将讨论两种模型的结合,既考虑自身退化的影响也考虑外部环境冲击的干扰,称之为退化冲击强度自回归移动平均模型(Autoregressive Moving Average Shock,简记为ARMAS(p,q)模型),其中参数p代表系统自身退化的阶数,q代表随机扰动的阶数。冲击模型研究的中心问题是系统失效时间或系统寿命。现有的文献都是以传统的冲击模型为主要考虑对象,如:
(i)逐次冲击的强度累积值落入某参数区域导致系统失效[3];
(ii)单个冲击的强度落入某参数区域导致系统失效[4,5];
(iii)相继k次冲击的强度均落入某参数区域导致系统失效[6]。
这些模型都是用来刻画在随机环境下工作系统的失败、维修等寿命现象。如置于动力车间中的精密仪表系统将会收到一些设备的运转所产生的随机冲击等。最近,许多具有Phase-type 分布的冲击模型被广泛研究。比如 Montoro-Cazorla et al.[7]应用 phase-type分布研究了具有策略N的冲击模型。 Montoro-Cazorla et al.[8]中提出了具有马尔科夫到达过程的冲击模型。Montoro-Cazorla and Pe′rez-Oco′n[9]又提出了具有三类维修的随机退化冲击模型。 还有许多关于冲击模型[10~12]的工作,详见Montoro-Cazorla and Pérez-Ocón[13], Montoro-Cazorla and Pérez-Ocón[14],Tang and Lam[15]。但这些工作均没有提出过对冲击强度作预测的模型,目前,仅有的两篇关于冲击强度的预测问题的文章是冲击模型中强度的预测和具有随机扰动强度冲击模型,但又都有一定的局限。本文建立了ARMAS(p,q)冲击强度估计的模型,克服了上面两篇文章的局限,并利用线性最小方差的方法给出了第η步冲击的强度预测值Yt+n|Yt,Yt-1…的置信度为1-α的置信区间。从而为保护系统能提前做出有效的预防。本文的结构如下:第一部分提出了退化冲击模型ARMAS(p,q);第二部分推导了退化冲击ARMAS(p,q)模型的方差;第三部分给出了退化冲击强度未来n步Yt+n的估计和正态假设下的模型的区间估计;最后是本文的结论。
1 退化冲击预测模型ARMAS(p,q)的建立
假设退化冲击系统不仅与以前时刻进入系统的自身值有关,而且还与以前进入系统的随机干扰存在一定的关系,Yt-1,Yt-2,…是已知自身的退化历史信息,εt,εt-1,εt-2,…是外部随机冲击干扰信息,且Yt是历史数据信息Yt-1,Yt-2,…及外部随机冲击信息εt,εt-1,εt-2,…的线性函数。线性最小方差预测公式比较简单,只要知道历史值Yt-1,Yt-2,…便可以得到任意步长的预测值,正因为模型的建模和预测的简单性,它成为预测中应用最广泛的方法。而且这种反映外部冲击持续影响的特性,线性模型是比较合理的。建模如下:Y1=φ1Yt-1+φ2Yt-2+…+φpYt-p+εt-θ1εt-1-…-θqεt-q,称此模型为自回归移动平均退化冲击模型,简记为:ARMAS(p,q)。此模型不仅考虑了自身的退化,也考虑了外部的冲击所带来的影响。
模型假设:
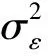
(2)φ=(φ1,…,φp)为模型的自回归系数,θ=(θ1,…,θq)为移动平均系数;
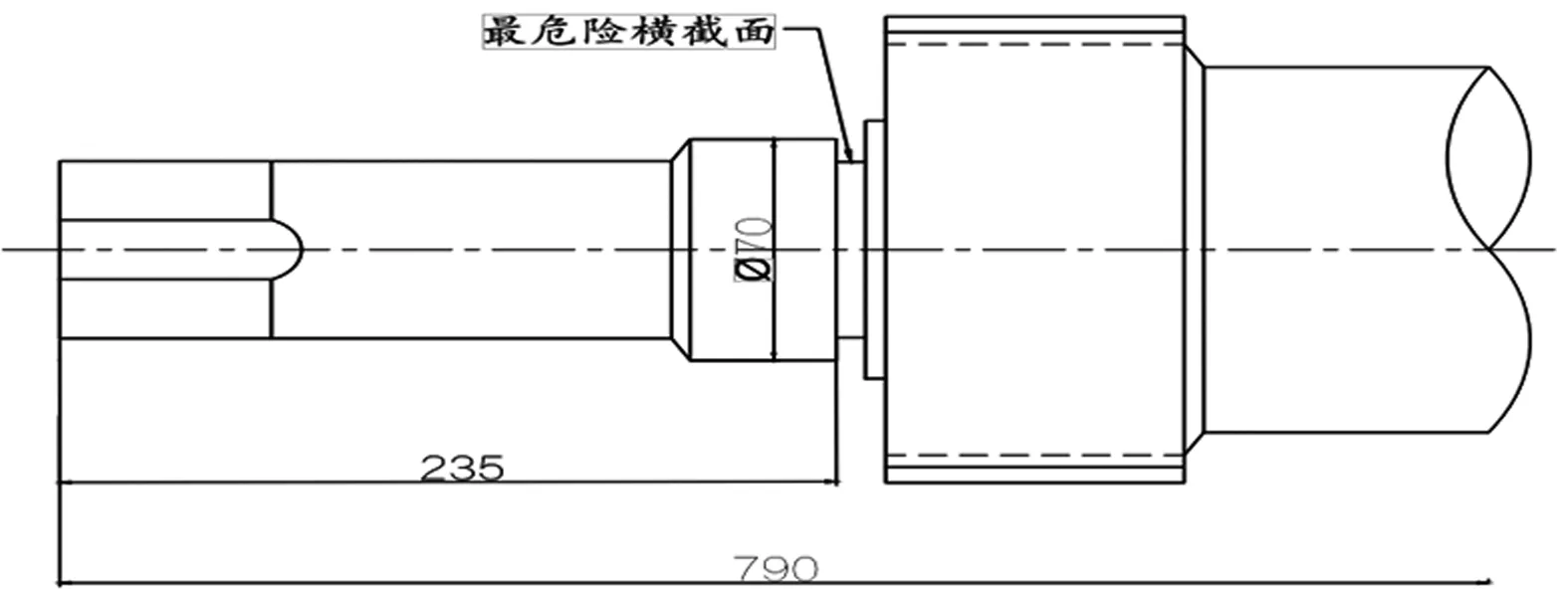
(3)εt与Yt-i(i=1,2,…)不相关。即EYSεt=0,∀S (4)φp≠0,θq≠0; (5)Yt由两部分构成,一部分依赖于自身退化信息Yt-1,Yt-2,…,令一部分则依赖于与自身退化信息Yt-1,Yt-2,…不相关的随机冲击干扰εt,εt-1,εt-2,…; (6)引进延迟算子B,退化冲击冲击ARMAS(p,q)模型可记为Φ(B)Yt=Θ(B)εt,称为自回归移动平均退化冲击模型。其中Φ(B)=1-φ1B-φ2B2-…-φpBp,Θ(B)=1-θ1B-θ2B2-…-θ2B2-…-θqBq,称为延迟算子多项式。且假设λi(i=1,…,p)为此差分方程的特征根,有|λi|<1。 显然,当q=0时,ARMAS(p,q)模型就退化成了ARS(p)模型;当p=0时,ARMAS(p,q)模型就退化成了MA(q)冲击模型。这两个特殊情况见参考文献[1,2]。 图1 轴向减速器截面图 定理1退化冲击模型ARMAS(p,q)的格林公式 因此模型ARMAS(p,q)的格林函数为 则称Gj为Green函数。 模型格林函数的意义: (1)退化冲击模型的格林函数Gj是前j个时间单位以前进入系统的外部冲击εt-j对系统Yt现在行为影响的权数,Gj越大,过去的冲击对t时刻系统Yt的影响也就越大。 (2)退化冲击模型的格林函数Gj刻画了系统Yt随时间变化的动态响应规律,是系统自身和外部环境影响的真实描述。 (3)退化冲击模型的格林函数Gj决定了外部冲击的影响权重,如果Gj→0(j→∞),则过去外部环境冲击的影响逐渐衰减。如果当→∞时,Gj不收敛于零,那么过去冲击的影响随时间推移而不衰减,显然,这样的系统方差将无穷大,是不平稳的,不是本文讨论的范围。 (2)预测的方差,由格林函数递推公式得: 未来三个时刻(步长均为1年)95%的置信区间如表所示: 表1 未来三个时刻(步长均为1年)95%的置信区间 图2 未来三期预测值Yt的走势及其置信区间 从表1中的数据和图2可看出,如果不在受到外界的随机冲击的影响,当期的冲击对未来的影响相对要逐渐减弱。当期的冲击对临近时刻的影响较大。这个与理论中给出的格林函数值的影响相符。 冲击模型本身在科学、技术、经济与管理等领域有广泛的应用前景,此模型的提出,为冲击模型的研究框架的进一步扩展提供了理论支撑,将使得更深刻的理论结果的出现和更重要的应用价值的产生成为可能。此模型不仅与以前时刻的自身冲击值有关,而且还与以前进入系统的随机干扰存在一定关系,扩展了冲击模型中强度的预测问题,这个问题的局限是模型仅与以前时刻的自身冲击有关。同时,也克服了仅仅讨论了将来系统与以前进入系统的随机干扰存在一定关系局限。本文提出的模型将两个模型的特点融合在一起,并结合历史数据信息,给出了冲击强度未来n步的预测值,并在正态假设下,推导出预测值的置信水平为1-α的置信区间。
2 ARMAS(p,q)退化冲击预测模型的方差
2.1 模型ARMAS(p,q)的Green函数及模型的方差




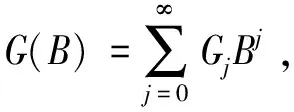

3 退化冲击ARMAS(p,q)模型未来n步Yt+n的预测
3.1 模型ARMAS(p,q)系统Yt的第n步预测值


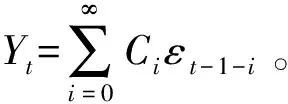
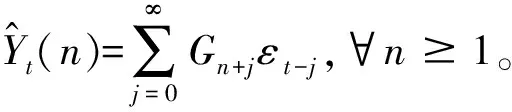


3.2 正态假设下退化冲击模型ARMAS(p,q)预测值Yt+n的置信区间


4 实例分析
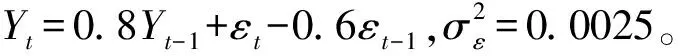

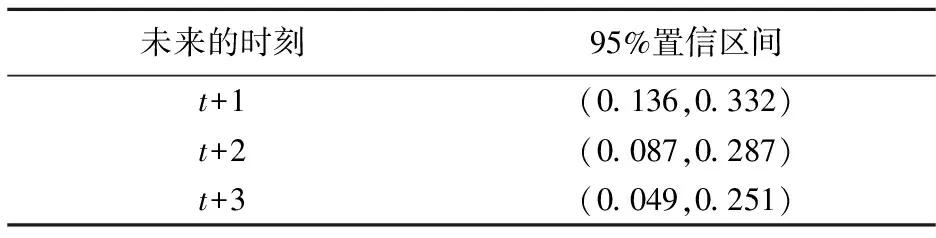

5 结论
