考虑制造成本扰动的闭环供应链回收与协调策略

曹晓刚, 黄 美, 闻 卉

(1.武汉纺织大学 管理学院,湖北 武汉 430073; 2.湖北工业大学 理学院,湖北 武汉 430068; 3.湖北省普通高校人文社会科学重点研究基地—企业决策支持研究中心,湖北 武汉 430073)

0 引言

近年来，各类突发事件层出不穷，而突发事件的频发对供应链产生了各种不同程度的影响。例如2008年汶川地震、雪灾、2010年玉树地震等事件导致交通中断，各种物资短缺，经济损失惨重；2011年11月泰国洪灾造成零件大量短缺，各国公司生产中断；2012年9月钓鱼岛事件造成大量公司销售严重受阻，产量大幅下降； 2012年6月伊利婴幼儿奶粉汞超标造成个别全优2、3、4段乳粉全部召回，市值一天内蒸发40亿元。因此，针对扰动事件的发生，如何采取有效策略协调供应链已成为许多学者重点关注的问题。

一些学者针对扰动事件对供应链进行了相关研究：吴海燕等[1]等人研究了具有竞争的制造商和零售商的闭环供应链生产决策，何波等[2]探讨了无制造成本扰动情形下的定价、订货策略以及最优调整策略，Huang 等[3,4]等探讨了双渠道供应链在突发事件干扰多种因素时如何生产和定价的问题。上述的研究并未涉及到突发事件干扰时的应对策略，因此一些学者也开展了此类问题(突发事件干扰下的应急管理)的研究： Zhang et al.[5]研究了供应链在需求扰动下的应急管理；覃艳华[6]，王玉燕[7]，徐浩等[8]，吴忠和等[9]，牟宗玉等[10]，李新然等[11]研究了闭环供应链在生产成本扰动下的协调策略；王旭等[12]，韩小花等[13]研究了竞争型闭环供应链应对突发事件干扰的策略。李新然等[14]，牟宗玉等[15]；王旭等[16]研究了突发事件同时干扰下的二级闭环供应链的应对问题；郑本荣等[17]主要考虑将回收成本采取分摊情形下的闭环供应链的决策问题。

王婷婷等[18]研究了基于博弈论的零售商产品回收问题；孙嘉轶等[19]探讨了突发事件干扰市场需求时的回收决策问题。孙丹丹等[20]构建了闭环供应链在不同回收类别的应急决策模型。赵琳等[21]比较了各类回收渠道的应急均衡决策问题。经有国等[22]刻画了扰动前后供应链的最优生产和定价决策。本文中，闭环供应链分为两周期，第一周期市场需求与新产品制造成本有关，而市场需求又对第二周期回收决策产生影响，故新产品制造成本会间接影响第二周期废旧产品的回收问题。本文与以往研究的不同点在于：当突发事件干扰第一周期新产品制造成本的情况下研究闭环供应链在集中与分散式决策下的协调以及回收决策问题。

2 模型描述与建立

本文建立的是由一个制造商和一个零售商组成的两周期闭环供应链系统。 制造商为Stackelberg博弈的领导者，主要负责新产品和废旧产品的制造和再制造，零售商为Stackelberg博弈的跟随者，主要负责废旧产品的回收以及新产品和再制造产品的销售。首先，该闭环供应链分为两个周期：第一周期和第二周期。第一周期中不涉及回收问题，只生产新产品；第二周期中既含新产品又含再制造产品。假设本文在信息完全对称情形下进行研究，且假设第二周期回收的废旧产品即为再制造产品的需求量，同时新产品和再制造产品不存在差异，即两者在市场上具有相同的销售价格。其次，闭环供应链的回收过程有计划期和实施期两个时期。在计划期，制造商和零售商根据预测结果决定废旧产品的回收策略，由于存在提前期，零售商在计划期就需回收废旧产品；在实施期，由于受扰动事件的干扰，实际产生的制造成本可能会与计划期的估计有所偏差。由于新产品制造成本的扰动会造成第二周期回收数量偏离原回收计划，令δg为回收数量的偏离量，当δg>0时，需高价购入废旧产品；当δg<0时，则需低价卖出废旧产品。因而，废旧产品回收数量的变化势必会引起闭环供应链原最优回收决策的改变，与此同时会增加一定的额外成本。本文相关的符号说明如下:

3 制造成本扰动下闭环供应链的回收与协调策略

3.1 集中决策模型

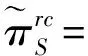
(x)+=max(0,x)

(1)

3.1.1 制造成本增大情形下的回收决策

制造成本增大也即新产品制造成本扰动量为正时的情形，根据上文定理1，可知当δ>0时，式(1)可化简为

(2)

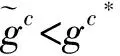
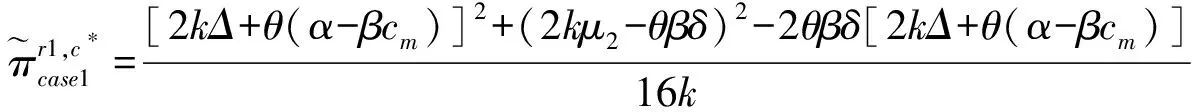
3.1.2 制造成本减少情形下的回收决策

制造成本减少也即新产品制造成本扰动量为负时的情形，同样根据上文定理1，可知当时，式(1)可化简为

有两种情况需要考虑：

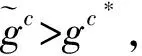
命题1当新产品制造成本的扰动量为δ时，闭环供应链在集中化决策下其废旧产品的最优回收数量为

零售商的最优回收价格为

此时，闭环供应链的最优回收利润为

3.2 分散决策模型

当突发事件干扰新产品制造成本后，分散化决策者可通过调整扰动前的回收决策来降低影响，但调整回收决策会产生一定的费用，此部分费用主要由回收计划的改变而产生。本文中零售商负责废旧产品的回收，故在此假设该成本由零售商承担。制造成本扰动下的分散化决策模型如下:

(3)

其中(x)+=max{0,x}。

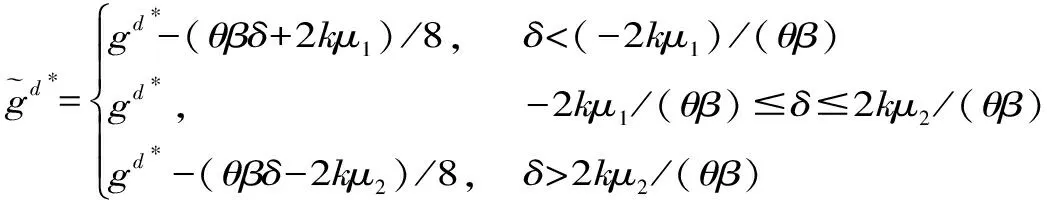
3.3 协调机制设计

(4)

(5)

命题3在制造成本扰动下，若两部收费契约能够协调闭环供应链的回收决策，则契约参数应满足:

则制造商再制造节约利润为

零售商回收利润为

4 算例分析

为比较两周期闭环供应链在制造成本扰动前后的回收决策及协调机制的变化，下面通过数值算例对上文得到的结论进行验证。本文假设相关参数α=100,β=1,cm=20,cr=10,θ=0.1,k=0.5,μ1=μ2=1。

根据相关参数的取值，可得到图1、图2(免)。

由图1、图2可知，当-10≤δ≤10时，最优回收数量与制造成本扰动前的结果一样，可知最优回收数量对制造成本的扰动具有鲁棒性，与结论3一致。当δ>10时，零售商最优回收价格随扰动量的增加而增加，最优回收数量随扰动量的增加而减少，δ<-10时，集中式决策下的最优回收价格随扰动量绝对值的增加而减少，最优回收数量随扰动量绝对值的增加而增加，而分散式决策下的最优回收价格在此范围内是小于零的。

本文取的值为16，14，12，10，8，6，4，2，0，-2，-4，-6，-8，-10，-12，-14，-16的情况下，集中式与分散式决策以及协调机制下相关的利润如表1所示(免)。

由表1可知制造成本扰动后，集中化决策者若采取无作为策略，其所获得的回收利润小于等于调整回收决策后闭环供应链所获得的回收利润。在分散化决策下，制造成本扰动后，当δ>10时，制造商调整决策后再制造节约利润高于回收计划不变时的利润，零售商调整回收决策后的回收利润低于回收计划不变时的利润；当δ<-10时，制造商再制造节约利润和零售商回收利润在调整决策后均提高了；当δ>0时，集中化决策下闭环供应链的回收利润、制造商再制造节约利润以及零售商回收利润均随制造成本扰动量的增加而减少；当-10≤δ<0时，集中化决策下闭环供应链的回收利润和制造商再制造节约利润随负扰动量绝对值的增加而增加，零售商回收利润随负扰动量绝对值的增加而减少；当δ≤-10时，集中化决策下闭环供应链的回收利润、制造商再制造节约利润以及零售商回收利润随制造成本负扰动量绝对值的增加而增加。制造成本扰动后，集中化决策下闭环供应链的回收利润仍高于分散化决策下制造商再制造节约利润与零售商回收利润之和，故设计了两部收费制契约协调扰动后的闭环供应链。当制造成本扰动时，采取契约协调后的利润是等于集中化决策下闭环供应链的总回收利润，故说明两部收费制契约能够很好地协调闭环供应链，提高整体效益。

5 结束语

本文以一个制造商和一个零售商组成的两周期闭环供应链为对象，研究了新产品制造成本受到不同扰动程度情形下的回收决策问题，并采用两部收费制契约协调扰动前后的闭环供应链，最后通过算例分析来验证协调契约的有效性以及最终结论的正确性。本文是在消费者对新产品和再制造产品的接受度相同且信息完全对称的情况下研究的，今后可进一步探讨差别定价、信息不完全对称等情况下闭环供应链应对突发事件干扰的回收决策及协调问题。同时本文只研究了制造成本这个单一因素的扰动问题，今后也可进一步研究再制造成本、回收成本以及多种因素扰动下的回收决策问题。