资源约束多项目调度问题研究现状与展望

彭武良, 黄 敏

(1.烟台大学经济管理学院,山东 烟台 264005;2.东北大学信息科学与工程学院,流程工业综合自动化国家重点实验室,辽宁 沈阳 110819)

1 引 言

在全球市场竞争的压力下,传统单项目管理方法已经难以满足企业创新和客户化生产活动需要,多项目管理理论和方法逐步被人们所接纳并成为顶尖的热门问题之一[1].在项目管理实践中,计划调度率先发生并处于首要位置,它引领各种项目管理职能的实现,是项目得以实施和完成的前提及依据.半个多世纪以来,基于经典资源约束项目调度问题(resource constrained project scheduling problem,RCPSP)的模型衍生和算法设计一直是项目管理和运筹学领域的研究热点,对单项目RCPSP 问题进行总体回顾和对RCPSP 特定问题分支进行综述的文献[2–6]不断出现.然而,这些都是针对单项目调度的,迄今为止尚未出现针对多项目调度问题的综述文献.

现代项目管理理论将多项目管理划分为战略层,策略层和执行层三个层次[1].其中项目组合管理处于战略层,其主要决策问题是项目投资和项目选择问题.策略层的项目管理形式一般认为是项目群管理,它对一组项目进行统一协调管理,其核心决策问题是资源配置和粗能力计划问题[7].而本文所专注的多项目调度问题则处于执行层,它致力于在内部任务逻辑约束和外部有限资源约束的条件下,合理安排任务的开始和完成时间,从而实现多项目总体目标的优化[8].多项目调度问题包含了单项目调度问题,其问题模型更为复杂,计算复杂度也更高.从上世纪末以来,随着多项目管理技术的广泛应用和计算机算法的不断发展,以资源约束多项目调度问题(resource constrained multi-project scheduling problem,RCMPSP)为代表的多项目调度问题逐渐成为学术界的研究热点,已经形成了两个清晰的分支: 集中式多项目调度问题(centralized RCMPSP,CRCMPSP)和分散式多项目调度问题(decentralized RCMPSP,DRCMPSP).二者都需要在共享资源约束下对多个并行项目进行调度.但CRCMPSP 将多个独立的项目组成一个大的项目,由一个多项目负责人基于全局信息对所有项目进行统一调度.而在DRCMPSP 中,每个项目由独立的项目负责人自行调度,不同项目之间的信息不透明,需要通过某种机制进行共享资源竞争.由于DCRMPSP 问题的提出,使RCMPSP 的研究呈现出诸多新的特征.因此,有必要在现阶段对其研究状态进行系统的总结归纳,夯实进一步深入研究的基础.本文专注于资源约束多项目调度问题的分析,突出多项目调度问题的特点,从各个维度对CRCMPSP和DRCMPSP 的研究现状进行梳理,给出资源约束多项目调度问题的完整研究视图.然后依据研究现状,分析目前研究中存在的主要问题,指出未来的发展方向,为RCMPSP 的进一步深入研究和推广应用提供参考.

2 集中式资源约束多项目调度问题

RCMPSP 的基本假设条件是项目之间不存在紧前关系,且不同项目的任务之间也不存在紧前关系.另外,研究人员通常假定多个项目是在一个集中环境下统一进行调度的.因此在DRCMPSP 问题出现之后,人们普遍将其称为CRCMPSP 问题以示区分.与后来出现的DRCMPSP 相比,多个项目统一调度是CRCMPSP的最显著特征.

2.1 问题描述

CRCMPSP 与RCPSP 问题相似, 项目内部活动之间存在着紧前关系约束和本地资源约束.因此, 很多RCPSP问题模型的衍生版本,如带有活动可中断,工期不确定或多执行模式等特征的RCPSP 问题,大都可以直接应用到CRCMPSP 中,本文不再详述.CRCMPSP 与RCPSP 的主要不同之处在于: 1)多项目调度除了对每个单项目进行优化之外,更重要的是对多项目共同目标进行优化.2)每个项目除了有本地资源约束之外,更重要的是要在项目之间竞争共享资源.因此,在介绍CRCMPSP 的典型问题模型之后,将从目标函数和资源利用两个方面对CRCMPSP 问题进行展开说明.

2.1.1 典型问题模型

CRCMPSP 管理多项目集合N,每个项目用p= 1,2,...,|N|表示,p ∈N.各个项目独立,不存在紧前关系.每个单项目p均可以表示为有向无环图Gp= (Vp,Ep),Vp为项目p的活动集合,每个活动pj ∈Vp用pj= 1,2,...,|Vp|表示.用Jp代表项目p的结束活动,即Jp=|Vp|.Ep为项目p中的紧前关系约束集合.若(pi,pj)∈Ep,则说明任务pi和pj之间存在紧前关系约束,要求活动pj必须在活动pi完成之后才能开始.活动pj的紧前任务集合表示为Epj.每个项目p有权重wp.全部N个项目共享K种可更新资源,其中第k种资源的供给量为Rk.活动pj对可更新资源k的需求量表示为rpjk.对于项目活动pj,其工期为dpj,开始时间和结束时间分别用spj和fpj表示.设At为多项目中在时间t上所有正在执行的多项目活动集合,典型CRCMPSP 的概念模型可以表示为[9]

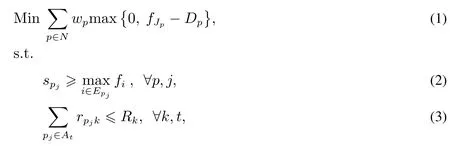
其中Dp为每个项目的截止日期,fJp为项目p结束活动Jp的完成时间,即项目p的工期.若项目p不能在截止日期Dp内完成,需要付出拖期惩罚wp(fJp −Dp).模型(1)最小化多项目拖期惩罚,约束条件(2)表示项目内部各活动之间的紧前关系约束,约束条件(3)限制了在任意时刻,多项目中的所有任务对每种资源的总需求不能超过其供应量.

2.1.2 CRCMPSP 的目标函数

非正规目标函数中包含了一些资源相关的目标函数, 如多项目资源水平, 鲁棒性等[17,18].但因为CRCMPSP 网络结构与单项目网络相同,所以其目标函数形式也与单项目调度问题大同小异,限于篇幅,不再赘述.对于现金流优化的目标函数,若只计算各个活动的现金流,那么多项目调度与单项目调度也是相同的.而Chiu 等[19]的处理方式则深入考虑了多项目调度的特点,构建了一种新的现金流优化模型,即

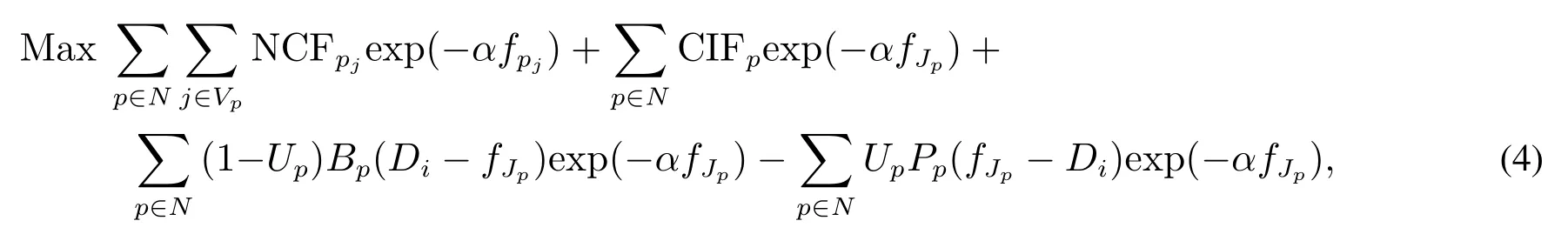
其中NCFpj为活动pj完成时的净现值,α为折扣率.CIFp为项目p完成时的现金流入.当项目拖期时,即fJp >Di,则Up=1,否则Up=0.Bp为项目提前完成时的单位时间奖励,Pp为项目拖期完成时的单位时间惩罚.式中的第一项与单项目净现值计算法方式相同,对每个活动计算折扣现金流并求和.式中第二项统计每个项目的净现值,第三项为多项目提前奖励,第四项为多项目拖期惩罚.该目标函数同时考虑了单项目和多项目的净现值,并且加入了每个项目延期惩罚和提前奖励,具有鲜明的多项目特征.

总之,与RCPSP 相比,CRCMPSP 问题的目标函数通常不是简单的多项目总工期,往往需要考虑每个单项目的调度目标,对单项目调度目标进行加权.项目权重可以直接确定,如式(1).也可以通过不同项目的不同拖期惩罚,或不同净现值来间接确定,如式(4).

2.1.3 CRCMPSP中的资源问题

CRCMPSP 的基本资源类型本质上与单项目RCPSP 相同,可分为三类: 可更新资源,不可更新资源和多重约束资源.在多项目调度问题中,又进一步分成共享资源和私有资源.但现有的研究通常只考虑研究价值比较高的共享可更新资源约束,仅有少数文献考虑不可更新资源约束[20,21].近年来,CRCMPSP 基于资源利用的新进展主要体现在柔性资源利用和考虑资源转移时间两个方面.

在项目调度问题中,人力资源往往会被特殊对待.其原因是人具有学习能力,能够在一个项目中胜任不同工种.这种能够胜任不同工种的人力资源被定义为多技能资源或柔性资源.而考虑多技能资源约束的项目调度问题称为柔性资源约束项目调度问题或多技能资源约束项目调度问题.Kazemipoor[16]对项目群调度进行研究,给出了一种多技能资源约束多项目调度问题,并提出了基于差分进化的求解算法.Chen 等[22]针对软件开发多项目管理的需求,构建了一个多技能共享资源池,综合考虑员工学习曲线,产品开发时间和成本,提出了一个多技能资源约束多项目调度问题,并采用快速非支配算法进行求解.事实上很多设备或加工中心也具有柔性,比如某种加工中心,既能用它进行车削加工,也能进行铣削加工,这个设备就可以被认为是柔性的[23].

另外,在多项目环境下,共享资源在项目之间乃至任务之间进行转移时,往往会需要额外的时间和成本.考虑到这种情况,Krger[12]提出了带有资源传递时间成本的多项目调度问题.若只考虑资源传递时间,需要在问题模型中增加如下约束条件,即

其中为项目m中的活动n作为资源传输方将资源k传递给项目p中的活动j所需的时间.为0-1 变量,=1 表示项目m中的活动n可以将资源k传递给项目p中的活动j,否则,=0.T为多项目工期.当=0 时,该式则构不成约束.

活动所需的资源不一定完全从紧前活动中获取,在特定时刻,需要决策活动所需资源可有多种来源: 1)从共享资源池中选取闲置资源,不需要等待,可以提前到位.2)从紧前活动中获取,需要等待.3)从其它活动中获取,需要等待.其中2)和3)的情况都需要满足式(5)的约束条件.Krger[20]深入研究了资源的多种转移方式,最复杂的情形是一种资源的转移会需要其它配套资源的占用,且同时产生资源转移时间和转移成本.

CRCMPSP 中多技能资源的使用与RCPSP 问题相同,而资源转移则是多项目调度的一种典型应用场景,更能够体现多项目调度的特点.因此,在调度目标和约束条件中考虑资源转移是当前CRCMPSP 问题研究中一个比较活跃的方向[24].

2.2 CRCMPSP 的求解算法

CRCMPSP 问题的求解算法可分为精确算法和近似算法两类.最早对RCMPSP 问题的求解是从精确算法开始的,如0-1 规划法[11]和整数规划法[25,26]等.RCMPSP 是强NP-Hard 问题,采用精确算法无法在多项式时间内对RCMPSP 的实际问题进行求解,只能借助于近似算法.近似算法本质上都是确定项目活动的优先值,发生资源竞争时,优先值较高的那个(或那些)活动能够率先被调度.近似算法一般都分为两个阶段: 第一个阶段确定活动的优先值或优先级排序.第二个阶段基于活动优先值生成调度计划.

近似算法又分为两种,一种是基于优先级规则的启发式算法,一种是元启发式算法或智能算法.二者的区别体现在第一个阶段,基于优先级规则的启发式算法采用某种启发式规则进行计算确定每个活动的优先级值,而元启发式算法致力于通过某种进化策略反复搜索得到最优的活动优先级排序.在近似算法的第二个阶段, 多项目与单项目的调度计划生成方法相同,主要包括串行调度生成算法(serial schedule generation scheme,SSGS)和并行调度生成算法(parallel schedule generation scheme,PSGS)[27].

既有的研究表明,SGSS 生成的是积极计划,PGSS 生成的是非延迟计划.非延迟计划是积极计划的子集, 有可能会错过最优解.因此, 在RCPSP 中, 多数研究使用的是SGSS.但Chaurasia 等[28]通过测试发现,SSGS 适合于活动数目较少的小规模项目,而PSGS 则在大规模项目中效率更高.CRCMPSP 与RCPSP 调度计划生成方法相同,但它包含了更多的活动,整体规模更大,因此PSGS 应该更具优势.

2.2.1 基于优先级规则的启发式算法

基于优先级规则的启发式算法是CRCMPSP 的主要近似算法.CRCMPSP 的很多优先级规则源于单项目RCPSP,形式上非常接近,但在性能上则有差别.既有研究表明,很多在单项目调度中比较高效的优先级规则在多项目环境下则表现较差,如最短任务优先(shortest operation first,SOF)[29].

在形式上与单项目RCPSP 问题完全相同的优先级规则很多.典型的是以关键路径时间为参数进行计算的优先级规则,如最小最晚完成时间MINLFT,最小最晚开始时间MINLST,最小最早开始时间MINEST,最小时差优先MINSLK 等都属于这一类.还有基于活动工期优先级规则,如最短任务优先SOF,最长任务优先MOF 等.基于多项目网络结构的优先级规则主要有最多后续任务MTS,最多紧后任务MCS.基于活动资源使用量构建的优先级规则主要有最小总工作量MINTWK,最大工作量MAXTWK 等[30].

还有一部分优先级规则针对了多项目调度的特点, 考虑活动隶属不同项目的情况, 如最短项目优先SASP = Min CPLp+dpj, 最长项目优先LALP = Max CPLp+dpj, 其中CPLp为项目p的关键路径长度.另外, 考虑到多项目网络活动较多, 单一规则容易计算得出相同优先级值的多个活动, 所以人们提出采用两种优先级规则组合计算活动优先值, 如最大工作量与最小最晚开始时间TWKLST =MAXTWK+MINLFT[14],最大工作量与最小最早开始时间TWKEST=MAXTWK+MINLFT[14].

很多文献对各种优先级规则的性能进行测试分析,但因为调度目标和所选算例的不同,性能测试结果也不尽相同.Kurtulus 的测试结果表明MAXTWK 和SASP 是目标函数为平均项目延迟时的最佳算法[30].Lova 等[14]的测试支持了这个结论,但同时指出若以多项目工期为调度目标,则MINLFT 表现最好.在寿涌毅的随机抽样算法中,MINSLK 是最高效的优先级规则[31].Browning 等[29]选用了在不同网络结构和资源强度的12 320 组多项目,对众多优先级规则进行了系统的测试比较,其结论是MINWCS 和TWK-LST 性能表现最好.

2.2.2 元启发式算法

元启发式算法在搜索最优活动优先级排序的时候,通常不使用活动工期,活动资源和多项目网络结构等信息.多数针对单项目RCPSP 问题的元启发式算法均可直接应用在CRCMPSP 中.就编码方式来说,在元启发式算法中,针对单项目RCPSP 的典型编码结构主要包括优先值编码和活动列表编码两种.其中优先值编码直接给出每个活动的优先值,而活动列表给出的是满足紧前关系约束的活动优先级排序.这两种编码方式均可直接应用到CRCMPSP 中,且各种进化或搜索策略也非常接近[18,32,33].

多项目调度与单项目调度相比有其特殊性,其项目活动数目较多,且每个项目往往有自己的工期底线,拖期会产生惩罚.Goncalves 等[34]考虑了这种特殊性,在其所提出的遗传算法中设计了一种新的编码结构如图1,其中n为活动数目,m为项目数.该编码结构分为三段: 第一段用于确定每个活动的优先值,与单项目调度问题的处理方式相同.第二段考虑到多项目中活动比较多,因此采用设置延迟时间,控制在并行调度的每次迭代中,只选择延迟时间较小的活动进行调度.第三段用于控制每个项目的发布时间.该算法基于PSGS 进行解码,通过遗传算法进化搜索最优解.文献[35]考虑了多个项目优先级的不同,组合基于活动列表和项目优先级值进行编码,采用SSGS 进行解码,通过混合遗传算法搜索多项目调度问题的最优解.

图1 编码结构Fig.1 Encoding of chromosome

近年来,国内学者对智能优化算法在CRCMPSP 的应用研究陆续出现,典型如遗传算法[32,35],蚁群算法[36]和粒子群算法[37]等.另外, 人们尝试将各种智能算法应用到CRCMPSP 多目标优化问题的求解中.如Rong 等[38]针对IT 产品开发项目的特点,构建了以成本,时间和技能增长为优化目标的三目标问题模型,并采用快速非支配遗传算法对该问题进行求解.

总之,目前国内外在CRCMPSP 的元启发式算法研究上与单项目RCPSP 相比还不够系统.既有的研究通常参照RCPSP 的算法结构,然后针对多项目调度目标的特点,在编码方式和其它算子上考虑多项目调度的特点.但CRCMPSP 的元启发式算法研究未能像RCPSP 问题那样形成广泛推崇的典型编码方式和搜索策略.

2.3 关键链方法在CRCMPSP 上的应用

关键链项目管理考虑了人的行为因素对项目进度计划的影响,在项目管理中体现了科学和艺术的结合,被认为是项目管理技术的一个重要进展.近年来,关键链方法在CRCMPSP 上的应用研究开始出现[18,39].多项目关键链调度沿袭了单项目关键链调度的三种缓冲类型: 输入缓冲,资源缓冲和项目缓冲.其中输入缓冲的设置与单项目完全相同,且设置在单项目内部,项目缓冲设置在每个项目工期结束处.此外多项目调度还需要设置多项目共同的多项目缓冲,设置在多项目工期结束处.多项目调度中的资源缓冲则分为两类: 一类是基于本地资源设置的内部资源缓冲.另一类是基于共享资源设置的能力缓冲,即项目间资源缓冲.出于简化的考虑,通常并不设置全部所有类型的缓冲.在多项目关键链调度中,多项目缓冲和能力缓冲是多项目关键链调度区别于单项目关键链调度的两个主要特征,应该着重予以考虑.李俊亭等[40]提出了一种考虑了多项目缓冲和能力缓冲的关键链多项目调度问题模型,以尽量去除活动的自由时间和减少资源在项目间转移为目标进行优化,设计了基于优先级规则的启发式算法.

关键链方法本身是一种朴素的管理思想,但对其优化调度则是一个复杂的难题.其原因在于各种缓冲区的嵌入会打乱原有的调度导致调度计划不可行[41].在单项目的项目缓冲,输入缓冲和资源缓冲的基础上,多项目增加了项目之间的能力缓冲,进一步提升了优化调度的难度.因此在现有的研究中,都存在一定程度的简化.比如在文献[18,21]的研究中,仅仅考虑了项目缓冲和输入缓冲,未考虑更为复杂的资源缓冲.文献[40]突出了能力缓冲在多项目调度中的功能,将能力缓冲与关键活动合并,方便了资源冲突解决,但没有说明输入缓冲的处理办法.

基于既有的文献分析可见,目前的多项目关键链调度还处于探索阶段,缺乏比较完善的优化调度路线,更缺乏严谨的形式化数学模型.总之,基于多项目的关键链管理方法还不完善[5].在这种情况下,如何突出能力缓冲的关键地位,对多项目关键链调度问题的模型和算法进行系统的研究,将是CRCMPSP 的一个重要发展方向.

2.4 多模式资源约束多项目调度问题

如果在CRCMPSP中,允许考虑项目活动可以按照不同的执行模式执行,则该问题就演变成了多模式资源约束多项目调度问题(multi-mode resource constrained multiple project scheduling problem, MRCMPSP).该问题是CRCMPSP 和MRCPSP(multi-mode resource constrained project scheduling problem)的结合,功能更为强大, 其优化调度的难度也相应较高.由于该问题的代表性和求解难度, MISTA 2013 挑战赛中专门将其作为竞赛题目,吸引了众多算法参赛,包括很多启发式算法和进化算法[42].Wauters 等对MISTA 2013 挑战赛中MRCMPSP 的多种算法进行了分析和总结, 为后续研究奠定了基础[42].在MISTA 2013 挑战赛中,Asta 等[43]的蒙特卡罗超启发式算法表现最好.其后,Asta 等对该算法进行了系统的完善,并对算法的关键环节, 比如蒙特卡罗树, 超启发式和更宽广的邻域搜索等进行了深入的讨论.Geiger[44]应用多线程技术对原MISTA 2013 挑战赛中排名第二的变邻域搜索算法进行了改进,进一步提高了算法的性能.MISTA 2013挑战赛中排名第三的算法是Toffolo 的整数规划算法[45].

MRCMPSP 因其求解难度逐渐引起了算法研究领域的关注,但在既有的研究成果中,各种典型进化算法的研究还不够充分.如何结合问题的特点,充分发挥各种进化策略的优势,结合各种优先级规则,提高算法的求解效率和质量将是MRCMPSP 研究的一个热点问题.

2.5 CRCMPSP 问题库

鉴于CRCMPSP 问题与单项目RCPSP 问题的相似性,很多学者在研究CRCMPSP 问题算法时,采用单项目RCPSP 问题库(PSPLib)的单项目问题实例进行组合,形成多项目实例[19,34].文献[14]基于多项目资源特征参数生成多项目调度问题实例,但没有考虑到多项目网络结构特征和项目权重.文献[29]全面考虑多项目的各种特征参数,构建了一种全新的多项目问题库.该问题库包含了12 320 个问题,每个问题包含3 个项目,每个项目包含20 个活动,使用4 种共享资源,每个项目都采用设计结构矩阵表示.该问题库公开在网络上(http://sbuweb.tcu.edu/tbrowning/RCMPSPinstances.htm),是到目前为止针对CRCMPSP 问题研究最全面的公开问题库.

3 分散式资源约束多项目调度问题

CRCMPSP 虽然也考虑了单项目的截止日期或项目之间的资源转移,但仍然在很大程度上忽略了单个项目的自身诉求.实际上,在项目型组织结构下,单项目负责人对所负责的项目拥有很大的自主权,且多项目往往会在分布式环境下执行.针对这种情况,Confessore 等[46]在CRCMPSP 研究的基础上,进一步提出了一种新的多项目调度形式—分散式资源约束多项目调度问题.DRCMPSP 呈现出显著的新特点,且具有明确的实用背景.因此自提出以来,被引起广泛关注,出现了很多对其进行介绍的文章[47−49].DRCMPSP 的最显著特征是要求多项目中的每个项目各自独立进行调度,其资源处理方式和调度过程与CRCMPSP 明显不同.

3.1 问题描述

在目前的研究中,人们对DRCMPSP 的定性描述较多,形式化建模较少.本文从DRCMPSP 的资源处理方式和决策机制入手对其进行系统的分析,然后归纳出DRCMPSP 的优化问题模型.

3.1.1 资源处理方式

DRCMPSP 更加明确地界定了本地资源和全局资源,从资源从属关系上把资源划分为三种类型: 1)本地资源,仅供特定单项目使用的私有资源,不能被其它项目分享.2)全局共享资源,隶属于所有多项目,属于全局资源,在多项目执行期间,可以在任意时段分配给任意项目.3)全局专属资源,隶属于所有多项目,属于全局资源,但每个单位资源一旦分配给某个项目,便只能在多项目周期内被该项目独占.

虽然CRCMPSP 中也区分本地资源和全局资源,但在既有的研究中,都只关注共享资源,这通常也是集中式多项目执行的实际情况.但在DRCMPSP 中则不同,各个项目之间都有自己的本地资源,仅竞争有限的全局共享资源.文献[50,51]对基于专属资源利用的分散式多项目调度进行了研究,构建了问题模型并提出了相应的近似算法.但在目前大多数DRCMPSP 研究中,都没有考虑全局专属资源的情况.因此在后续对DRCMPSP 研究现状的分析中,将只针对使用本地资源和全局共享资源的多项目场景.

3.1.2 决策机制

DRCMPSP 决策过程是一种分布式决策过程,其决策机制至少分为两层: 1)本地决策.每个项目均由项目负责人自行调度,决策所需的信息是内部项目私有数据,不同项目负责人无法知晓其它项目的决策情况.2)全局决策.全局决策的目标是对共享资源在多个项目之间的使用进行分配.因为每个项目都单独进行调度,在共享资源利用上会发生冲突.共享资源协调机制会根据多项目调度的总体目标,平衡共享资源在多个项目不同时段的使用情况.

Wang 等[47]按决策顺序定义了三种决策模型: 1)从上向下,即先进行全局资源分配,然后进行本地决策.2)从下向上,也就是先进行本地决策,后进行全局决策.3)平等协商,各个项目自行调度,相互协商共享资源的使用.需要指出的是,在DRCMPSP 中,无论是按照从上到下还是从下到上的顺序进行决策,都不可能一蹴而就,均需要反复迭代才能完成共享资源的最优分配.在平等协商模型中,若各个项目之间信息不透明,一对一或一对多进行协商对算法的复杂度要求太高.从目前的研究来看,主要以从上向下和从下向上两种决策模型为主,二者均是典型的双层计划调度方式,也比较符合大多数多项目管理的实际情况.

3.1.3 问题模型

到目前为止,各种文献中关于DRCMPSP 的描述还没有形成一个统一框架.本文从DRCMPSP 的定义出发,基于DRCMPSP 的资源处理方式和决策机制,给出基本的DRCMPSP 问题的概念模型,该模型分为全局决策层式(6)～式(11)和本地决策层式(12)～式(16),即

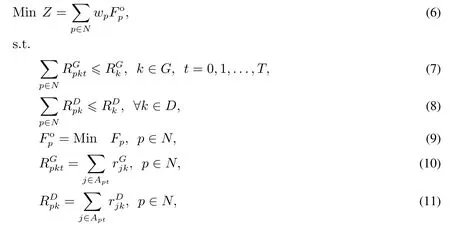
其中式(6)为多项目目标函数,基于单项目调度结果及其权重wp计算.式(7)为全局共享资源约束,要求每种资源k在每个时刻t分配给各个项目的资源量不能超过该资源的总量,其中G为全局共享资源集合,为全局共享资源k的供应量,为在t时刻分配给项目p的共享资源k的数量.式(8)为全局专属资源约束,要求分配给所有项目的全局专属资源量之和不能超过该资源的总量.其中D为全局专属资源集合,为全局专属资源k的供应量,为分配给项目p的全局专属资源数量.等式约束(9)中,的取值为单项目调度层每个项目p的调度结果.式(10)为每个项目的取值,仍然依赖于单项目调度层每个项目p的调度结果,其中Apt意义同前,为项目p在t时刻正在执行的活动集合.为活动j对全局共享资源k的需求,k∈G.等式(11)为每个项目的取值,依赖于单项目调度层每个项目p的调度结果,为活动j对全局专属资源k的需求,∀k∈D.

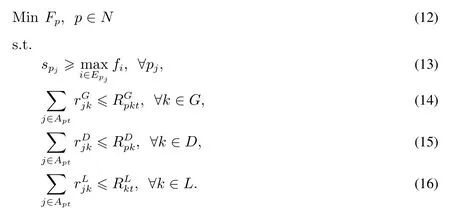
在本地决策层,式(12)为单项目调度目标函数.式(13)为单项目p中活动的紧前关系约束,spj为项目p中活动j的开始时间,Epj为该活动的紧前活动集合,fi为其某个紧前活动i的完成时间.式(14)为项目p的全局共享资源约束.式(15)为项目p的全局专属资源约束.式(16)为项目i的本地资源约束,L为本地资源集合,为本地资源k的供应量,为活动j对本地资源的需求量.

在全局决策层,DRCMPSP 的目标函数与CRCMPSP 一致,可以使用CRCMPSP 的各种目标函数.而本地决策层本质上一个是个单项目RCPSP 问题,区别在于其全局共享资源的供应量在项目周期的各个时段是不同的.单项目之间在本地决策时独立,但本地决策依赖于全局决策的共享资源分配方案,全局决策依赖于本地决策的单项目目标和共享资源需求.

3.2 DRCMPSP的求解方法

在DRCMPSP 中,本地决策的单项目调度问题和全局决策的资源分配问题都是NP-Hard 的问题.其中应用各种近似算法求解本地层的单项目RCPSP 问题已不再是DRCMPSP 的主要矛盾.DRCMPSP 问题求解算法的难点是解决全局共享资源的最优分配问题, 其原因在于全局共享资源竞争的情况更为复杂, 需要同时确定每单位资源在每个时段的分配情况.若在多项目中有全局共享资源集合G, 资源k的供应量为在整个项目周期内,会有个单位时间资源需要分配.若从上向下分配这些资源,在全局层无法确切知晓每个单项目在哪些时段需要的资源量.反之,若从下向上竞争这些资源,在本地决策层无法知晓其它项目是不是也在特定时段需要这些资源.因此,求解DRCMPSP 无法像CRCMPSP 一样只要确定活动的优先级即可生成完整的多项目调度计划,它必须采取多阶段反复迭代的方式才能实现全局共享资源的分配.

可见,与CRCMPSP 相比,DRCMPSP 算法的瓶颈体现在全局共享资源的分配(或竞争)上,既有的DRCMPSP 研究大都聚焦于此[46,49,52−54].从目前的研究来看,DRCMPSP 共享资源冲突解决的各种方法差别很大,总体来看大致有两种思路: 基于市场的方法(market-based approach)和基于协商的方法(negotiation-based approach).通常二者均基于多代理系统(multi-agent system,MAS)实现.

3.2.1 基于市场的方法

基于市场的方法可以被认为是一种从下向上的决策过程,其出发点是各个项目竞争共享资源,紧缺共享资源在紧缺时段的价格会被抬升,从而引导自行调度的各个项目在成本的压力下进行变通,通过调整活动的执行时间改变全局共享资源的占用时段,最终达到解决资源冲突的目的.通常采用多代理的方式实现,为每个项目设置一个代理作为竞拍者,负责单项目调度,并在每一轮竞标时发出竞标书.竞标书中含有对资源的报价,以及在每个时段对共享资源的需求量.为共享资源设置代理作为拍卖人,致力于在每一轮以最高的价格将资源拍卖出去.这种方法类似于自由市场的拍卖过程,因此基于市场的方法也称为基于组合拍卖的方法.

Confessore 等[46]为每个项目设置一个代理(竞拍者)负责该项目的调度并参与共享资源的竞标.为共享资源设置一个代理(拍卖者)执行组合拍卖算法,决定每轮竞标的胜出者.通过计算实验,证明该算法可以解决最多5 个项目每个项目8 个任务的小规模DRCMPSP 问题.Confessore 等[52]进一步完善了算法的流程,并将基于市场的方法与基于优先级规则的算法进行了比较,验证了算法的有效性.目前基于组合拍卖方法的DRCMPSP 在思路上是相同的,但处理细节上往往区别很大.其中Confessore[52],Ara´uzo[53]和王磊等[54]的处理方式相对比较接近.本文以文献[52]的算法结构为基础说明基于组合拍卖的DRCMPSP 问题求解过程,如图2.

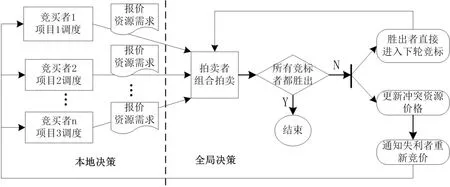
图2 基于组合拍卖的多代理系统结构Fig.2 Multi-agent system architecture based on combination auction

拍卖者将全局共享资源在每个时段的单位供应量作为拍卖品.每个单位资源在每个时间单位均为一个独立的拍卖品.这样,对于每种资源k,∀k ∈G,在多项目工期T内,会产生种拍卖品.首先设定资源拍卖价格,通知竞拍者.每个竞拍者在工期,本地资源和全局资源的约束下,以某种单项目目标进行单项目调度.调度完成之后,将报价,对共享资源在每个时段的需求和调度结果传递给拍卖者.拍卖者以总价最高为目标进行组合拍卖,约束条件是每个拍卖品只分配给一个竞拍者.若所有竞拍者均胜出,则算法结束.否则,调整资源价格,要求失利者重新调度.待所有失利者重新调度完毕,再次与胜出者重新竞标.拍卖者组织进行新一轮的组合拍卖,直到所有竞拍者胜出.最后根据每个竞拍者的调度结果,计算多项目总体目标.

类似的研究还有文献[55–60]等.现有的基于市场的方法都采用MAS 的架构,在全局决策层采用组合拍卖的方式实施价格引导.由于组合拍卖问题本身就是一个NP-Hard 问题,所以针对大规模DRCMPSP 问题设计高效的组合拍卖算法将是未来的一个主要研究方向.

3.2.2 基于协商的方法

与基于市场的方法类似,基于协商的方法也多采用MAS 实现.通常在本地决策层为每个项目设置项目代理,在全局决策层为共享资源设置协调代理(中介代理).在基于市场的方法中,单轮竞争的胜出者只是暂时的胜利,在后续轮次中还需要继续参与竞争.而在基于协商的方法中,一旦某个项目胜出,则直接获得共享资源的使用权,不再参与竞争.

由于DRCMPSP 问题本身的复杂性,在既有的研究中,协商的方法也不尽相同.但一般都在全局决策层设置协调代理,在本地决策层为每个项目设置项目代理.协调代理负责共享资源分配方案,其对资源的分配是强制性的,项目代理必须执行.其典型结构如图3.

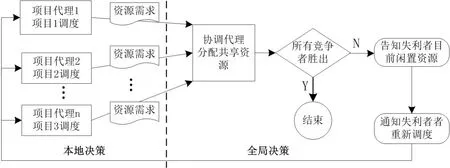
图3 基于协商的多代理结构Fig.3 Multi-agent system architecture based on negotiation

Homberger[62]进一步提出了一种基于进化算法的中介代理机制,思路是通过进化算法搜索最优或近优的项目订单列表(项目对共享资源的需求).项目代理使用属于自己的项目订单进行调度产生可行的项目调度计划,并提交调度结果给协调代理,实验结果表明,计算效率明显得到提升.Homberger 的方法强化了协调代理的权利,是一种统一协调的方法[61,62].在文献[63]中,通过多个Agent 之间交换附加信息的手段提高算法收敛速度和求解质量.但在DRCMPSP 中应该公开什么哪些信息尚无定论,需要根据具体应用场景而定.文献[64]提出了一种带有单边支付的自动协商方法,引导项目代理通过支付一定的成本赢得其它代理对其资源要求的认可,但项目代理需要事先生成基于多种调度计划以供协商时选择.

资源分配是一个协商的过程,也是各个项目代理之间进行博弈的过程[65].Wauters 等[66]以多项目总工期最短为目标,将分散博弈引入中介代理进行全局共享资源分配,中介代理管理项目订单列表和项目代理提交的调度信息,通过项目订单列表和每个项目的活动列表,对全局共享资源进行分配.这种方法的问题求解速度很快,但它假定每个项目代理的详细调度信息对中介代理是透明的.李飞飞等[67]以多项目总延期成本为优化目标,设计了多回合序贯博弈谈判机制,基于多项目总体目标决定每个回合的胜出者.胜出者退出,失利者基于剩余资源继续调度并参与博弈.与Homberger 的方法相比,在基于博弈的协调过程中,各个项目代理会提供多种调度方案,每种方案对多项目(隐含其它项目)和本身有不同的收益.项目代理之间基于某种协议进行博弈,胜出者退出,失利者需要重新调度.

与基于市场的方法相比,基于协商的方法的特点有二: 1)在基于协商的方法中,项目代理与中介代理按照某种协议进行协调直接进行共享资源分配,而不是通过抬高共享资源价格进行间接引导.2)基于协商的方法为了方便全局层决策或与其它项目协商,通常会要求单项目公开一定的私有信息.如何在资源竞争时确定胜出者取决于DRCMPSP 的多项目调度目标函数.而如何确定私有信息的公开程度,则需要在算法效率和实际需求之间进行权衡.

3.3 DRCMPSP 问题库

很多DRCMPSP 研究通过项目实例或基于单项目调度算例组合形成DRCMPSP 问题实例, 但这不利于不同算法的性能比较.为此, Homberger 构建了一个包含140 个实例的DRCMPSP 问题库并在网络上公开(http://www.mpsplib.com)[61].多项目实例中分别包含了2,5,10 和20 个单项目实例,共享资源分别包括1,2,3 和4 种.单项目实例来源于单项目问题库PSPLib(http://www.om-db.wi.tum.de/psplib)[68].该问题库从2007年公开以来,引起了广泛关注,截止到目前已发布了140 余种算法和测试结果.

4 分析与展望

从被提出的时间顺序和成熟度来看,单项目RCPSP 最早,之后是CRCMPSP 和DRCMPSP.三者存在着包含和被包含关系,但不存在着替代的关系.三者的总体比较如表1.CRCMPSP 和DRCMPSP 均包含多个单项目RCPSP 实例.CRCMPSP 可将多个项目合并形成一个超级项目网络,而DRCMPSP 则维持各个单项目的独立决策.CRCMPSP 通常只关注多项目总体目标,而DRCMPSP 则同时优化多项目和单项目.单项目RCPSP 和CRCMPSP 都只由一个负责人决策,而DRCMPSP 则由多个单项目负责人和多项目总负责人协同决策完成.所关注的资源,算法和所使用的问题库也各不相同.

表1 典型项目调度问题的比较Table 1 Comparison of classic project scheduling problem

如前所述,单项目RCPSP,CRCMPSP 和DRCMPSP 的历史积淀不同,因此其成熟度也各不相同.其中最成熟的单项目RCPSP发展路线图可成为后两者的直接参考.尤其是CRCMPSP 问题,未来的发展必然会随着单项目RCPSP 的发展而发展,主要体现在两个方面:

1)CRCMPSP 问题模型的研究.与单项目RCPSP 相同,CRCMPSP 的问题模型可以基于目标函数,资源处理方式和活动执行方式等方面进行扩展.而在目标函数和约束条件中考虑资源转移的多种情形能够体现多项目调度的特点,是实现多项目调度问题理论与应用契合的关键,因此有必要对其进行更深入的研究.另外,综合考虑项目缓冲,输入缓冲,单项目内部的资源缓冲和多项目之间的能力缓冲,构建多项目关键链调度的优化问题模型,仍然是目前该领域的一个研究难点.

2)CRCMPSP 求解算法的研究.与单项目RCPSP 问题相比,CRCMPSP 问题求解难度更高,需要借助于近似算法.在目前的CRCMPSP 近似算法中,基于优先级规则的启发式算法研究相对较多.而元启发式算法,或结合智能算法和优先级规则的混合算法在CRMPSP 中的应用研究还不够深入.多项目的关键链调度因为涉及额外的缓冲设置操作,对算法的设计提出了更高的要求.因此,基于最新的智能算法进行改进,设计更加高效的求解算法,必然是未来的一个重要研究方向.

对于DRCMPSP 而言,虽然人们近年来对其进行了很多研究,但当前的成熟度还比较低,具有更加开阔的研究空间,主要表现在以下几个方面:

1)虽然人们提出了几种典型的DRCMPSP 求解策略,但到目前为止,大部分求解算法都还只能求解小规模DRCMPSP 问题.因此,研究DRCMPSP 问题的高效求解算法是DRCMPSP 的首要发展趋势.

2)既有的算法中,能够在本地决策层应用单项目RCPSP 方法进行单项目调度,但在全局决策层的共享资源分配上,无论是启发式规则还是智能算法的应用研究都还非常欠缺.因此作者认为,在共享资源分配上实现基于优先级规则或智能算法的近似算法研究,具有广阔的研究前景.

3)在共享资源分配(或竞争)上,目前的主流算法比如基于市场的方法和基于协商的方法,提升空间都还很大.比如在基于市场的方法中,所使用的组合拍卖方法本身就是一个复杂的NP-Hard 问题,其价格调整策略也有很多种,如何设计和评价并选择适合于DRCMPSP 问题本身的组合拍卖算法,目前还没有统一的框架.在基于协商的方法中,如何面对多项目调度目标设定协商规则,或如何设计高效的博弈方法,都还需要进一步深入研究.

4)另外,在DRCMPSP 中,单项目通常只在竞争共享资源时与全局决策层代理或其它项目发生关系.但既有研究表明,适度公开单项目的私有信息,会明显加快算法的求解速度.而如何在保持DRCMPSP 问题本质特征的基础上,确定公开单项目私有信息的程度,还需要进行测试和进一步的界定.

总体来看,DRCMPSP 无论在问题模型还是在调度方法上,均与既有的RCPSP 和CRCMPSP 问题有了明显的不同,是近年来多项目调度问题研究的一个重要进展.它具有明显的分层机制,单项目层按照单项目目标独立调度,并在多项目层面向多项目总体目标进行协调,在分布式多项目管理中具有非常好的实际应用前景.在求解算法上,除了能够利用CRCMPSP 的既有算法之外,多代理技术,博弈论和组合拍卖算法等均有充分的理论发挥空间.因此,对DRCMPSP 的深入研究将是多项目调度问题的一个重要研究主题和主要发展趋势.

5 结束语

项目管理是一个非常活跃的研究领域,项目调度作为项目管理的核心内容,也得到了业界和学术界的广泛关注.但现今项目规模越来越大,项目数目越来越多,仅仅依靠传统的单项目计划方法往往不能满足现代多项目管理实践的要求.因此,人们从执行层到策略层对资源约束多项目调度问题进行了深入的研究,提出了很多理论模型和求解算法.尽管多项目调度问题从上个世纪六十年代就已经被提出,但到目前为止,还缺乏对既有研究的深入分析和系统总结.

本文对多项目调度问题的两个分支CRCMPSP 问题和DRCMPSP 问题进行了界定,然后分别对两种问题的数学模型和求解算法进行了梳理,给出两个问题研究现状的总体视图.在此基础上,对单项目RCPSP,CRCMPSP 和DRCMPSP 问题进行系统比较,指出多项目调度问题研究目前存在的问题和未来发展方向.通过本文的研究,希望能够为多项目调度理论的深入研究提供更加直接的参考,为多项目调度理论体系的进一步发展完善提供助力.