网架结构单点冲击激励的数学模型与数值分析

邹 韬, 蔡晓丽, 伍晓顺

(江西理工大学 土木与测绘工程学院(南昌)， 南昌 330013)

大跨空间结构[1-3]类型丰富，服役数量多。由于跨度大、覆盖面积广，此类结构一旦破坏将产生严重后果。因此，应当对此类结构进行健康监测以便及时判断结构损伤和保证结构安全。动力测试是结构健康监测领域常用的技术手段，但该方法在应用于大跨空间结构时常遇到激振难题[4-5]。

目前大跨空间结构的激振方式大致可以分为两类。第一类是环境激励[6-9]，主要指风振激励。有些文献提到可以采用地震激励[10-11]，但地震激励在现实中遇到的概率较低。环境激励具有无需激振设备且激振能量大的优点，但也存在每次激励时被激发模态不固定、有时难以激发目标模态的缺点。第二类是人工激励，包括锤击激励、激振器激励、跳跃激励和阶跃激励等[12-16]。锤击激励利用力锤来激发结构的振动，输入能量小且难以保证激励方向。激振器激励可以输入较大能量，但在现场测试中设备安装较为困难。跳跃激励利用少数人在屋面上的跳跃激发结构的振动，可以主动控制跳跃的位置和快慢。阶跃激励采用突卸重物的方式使结构产生具有初始位移的自由振动，可以通过优化荷载分布激发特定模态。总的来说，锤击激励和激振器激励适用于室内模型试验，并不适用实际结构的现场测试。相比跳跃激励，阶跃激励可以较为精确地控制荷载分布从而实现激发特定模态的目的。但是，阶跃激励的激振效率较低，往往需要施加较大的重物荷载才能激发出较大的加速度幅值。

一般而言，较大的加速度幅值有利于增大采集信号的信噪比[17]，从而提高模态识别、模型修正和损伤识别等工作的精度。为了尽量利用较小的重物质量来使结构产生较大的加速度幅值，有必要对基于重物坠落的冲击激励新方法展开定量研究。本文将重物、绳索和结构视作一个模拟单点冲击激励的复杂振动系统，并推导该系统的振动方程。在求解振动方程得到单点冲击力时程的数学表达式后，以某1 200杆网架结构为例进行数值分析。重点考察重物质量、坠落高度、绳索弹性模量、绳索刚度和等效振动系统阻尼比对结构最大加速度幅值的影响，并与阶跃激励进行对比。

1 单点冲击激励的数学模型

1.1 模拟单点冲击激励的复杂振动系统

对于大跨空间结构，可以采用使重物突然坠落的方式对其施加冲击激励。基本流程为：① 悬挂重物，在激励位置(为竖向)悬挂重物，用绳索连接重物与节点处电磁铁，并将重物与松弛绳索抬高s1。② 释放重物，在重力作用下重物自由坠落，直到绳索张紧并达到足够大的冲击力将电磁铁拉开后结构开始振动。可以通过调整电压来设定不同的电磁铁吸力[18]。

在绳索刚张紧的瞬间，重物具有最大动能，且尚未传递给绳索。此时，根据能量守恒原理，重物的初速度为

(1)

式中：g为重力加速度；s1为绳索从开始坠落到绳索刚张紧瞬间的坠落高度。

绳索张紧后，重物下坠产生的动能将通过绳索传递到结构，使重物、绳索和结构一起发生振动。由于结构上的悬挂点存在有限刚度，因此悬挂点不能视作无限刚的边界，而应当视作一个弹簧(称为弹簧1)。弹簧1的刚度等于悬挂点(即激振点)对应自由度的结构刚度，且质量为零。张紧后的绳索也可视作一个弹簧(称为弹簧2)。弹簧2的刚度等于绳索的轴向刚度，其质量沿轴向均匀分布。可见，重物和两个弹簧构成了一个具有集中质量和分布质量的复杂振动系统，如图1所示。

图1 重物、绳索和结构构成的模拟单点冲击激励的复杂振动系统

Fig.1 Complicated system to simulate single-point impact excitation, which is composed of the weight, the cable and the structure

图1所示振动系统的参数简述如下：弹簧1的刚度、质量和长度分别记为k1，m1和l1；弹簧2的刚度、质量密度、质量和长度分别记为k2，ρ2，m2和l2；重物质量记为M。根据前述分析，可知m1=0，m2=ρ2l2。以绳索刚张紧时重物所在位置为零位移位置，并以坐标向下为正。

1.2 复杂振动系统的振动方程

忽略绳索质量对等效刚度k的响应，根据力的平衡方程，有

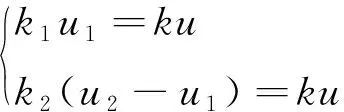
(2)

式中：u1，u2和u分别为O1，O2和O点的位移；u2=u。整理式(2)后分别得到

(3)

(4)

假设弹簧1、弹簧2在运动过程中是均匀变形的，弹簧1、弹簧2中任意一点距固定端ξ处的位移分别为

(5)

(6)

dT1=0,ξ∈[0,l1]

(7)

(8)

在t时刻，振动系统的动能等于重物和2个弹簧的动能之和，具体表达式为

(9)

在t时刻，振动系统的势能为

(10)

非保守力(重力可视作幅值为常数的外部激励)做功的变分为

(11)

将式(9)～式(11)代入Hamilton原理[19]

(12)

整理后得到振动方程为

(13)

2.3 冲击激励的时程

由式(13)得到振动系统的位移解为

(14)

(15)

(16)

(17)

式(16)、式(17)表明振动系统为简谐振动。在t≤0.5π/ωd时(即前1/4周期)，绳索张力的时程为

F=ku(t)=k1u1(t)

(18)

当t=0.5π/ωd时(即1/4自振周期处)，点O1处的位移u1达到最大值

(19)

相应地，冲击力在t=0.5π/ωd时达到最大，为Fmax=k1u1 max。通过调整电压，将悬挂点处电磁铁的最大承载力设置为Bmax=γk1u1 max，其中γ为不大于1的折减系数。在绳索张力达到Bmax时，绳索脱离电磁铁，对结构完成冲击激励并使结构开始自由振动。

2 数值算例

2.1 模型参数

以某60 m×45 m的正放四角锥平板网架为例进行数值分析，如图2所示。网架的结点数为326(其中支座结点数为16)，杆件数为1 200。考虑3种荷载工况(包括0.25 kN/m2静载、0.3 kN/m2活载和-0.5 kN/m2风载)，基于现行设计规范[20-21]进行网架的结构设计，以尽量贴近工程实际。杆件均为二力杆，采用的圆钢管规格从P75.5×3.75～P159.0×7.00不等。结点均为铰接点，采用直径为140～350 mm不等的螺栓球。钢材等级为Q235B，材料密度为7 850 kg/m3，弹性模量为2.06×1011N/m2。同时考虑静载、杆件质量和螺栓球质量对组集质量矩阵[22]的贡献。经模态分析[23]后得到前30阶模态频率，如表1所示。

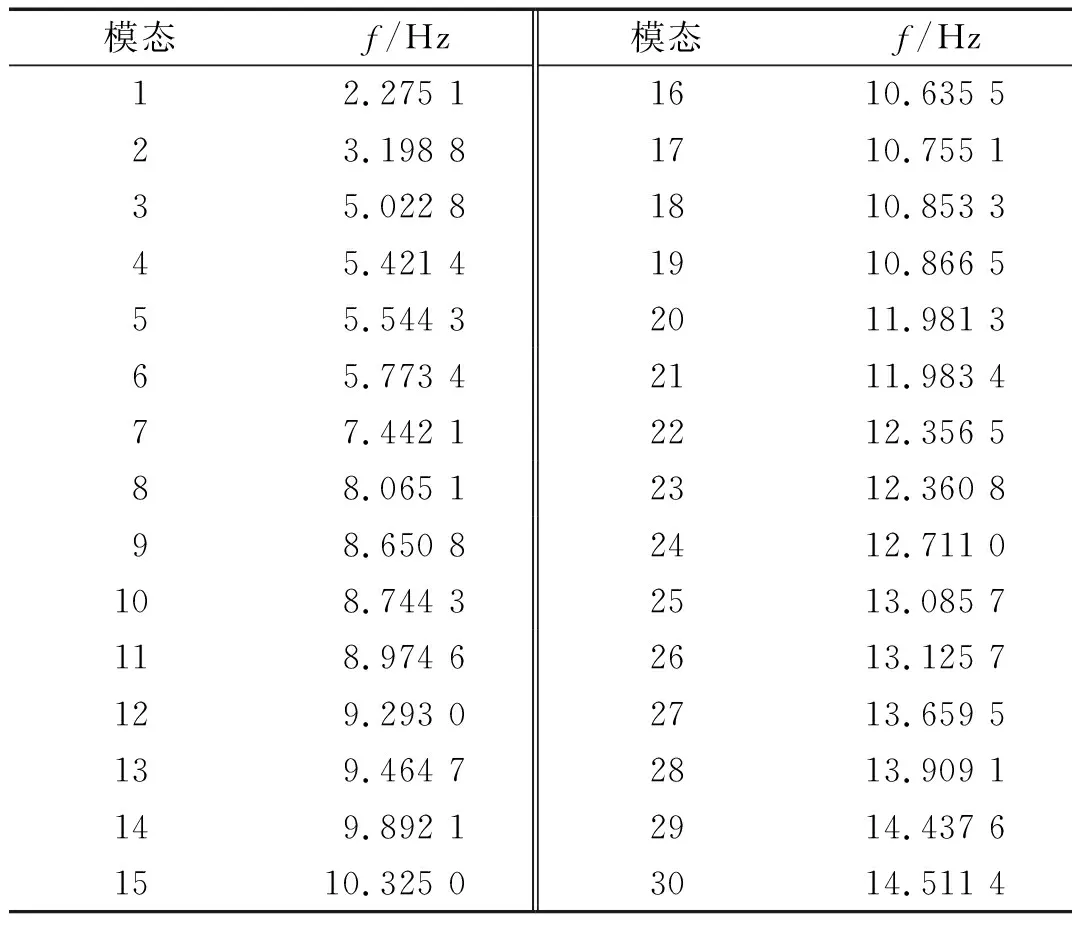
表1 网架结构前30阶自振频率

2.2 冲击力时程与加速度幅值

鉴于各节点竖向刚度的变化范围为4.082 9× 107～1.4158×108kN/m，差异不大。不妨以具有适中刚度的159号节点(图2中实心圆所示位置)作为重物悬挂点(即激励点)。网架结构在悬挂点位置的竖向刚度为k1=8.166×107N/m(对应图1所示振动系统的弹簧1刚度)。假设绳索的弹性模量为E=1.0×1011N/m2，截面面积为A2=78.5 mm2，绳索张紧长度为1.0 m(等于重物抬高高度s1)，绳索质量密度为7 850 kg/m3，重物质量为3 kg，振动系统的阻尼比为ζ=0.05，则张紧后的绳索刚度为k2=7.85×106N/m(对应图1所示振动系统的弹簧2刚度)。不妨取γ=1.0。将这些参数带入式(18)计算冲击力时程，并将计算结果绘于图3。不难发现，冲击力的幅值很大，高达19.7 kN，但作用时间非常短，仅有1.04 ms。

图2 某60 m×45 m平板网架(mm)

在159z自由度(对应159号结点z向)施加图3所示的冲击力时程，并采用Newmark-β法计算响应时程。假设网架结构各阶模态的阻尼比均为0.02，采样频率为50 kHz，采样时长 0.5 s。最大加速度幅值为4.82 m/s2，所在位置与激励点相同，对应的加速度时程如图4所示。而第二大加速度幅值为1.51 m/s2，可见单点冲击激励可使激励点处的加速度幅值远高于其他自由度。

在159z自由度施加阶跃激励，最大加速度幅值同样出现在该自由度。为了与冲击激励产生相同的最大加速度幅值，阶跃激励需要的重物质量为 368 kg，约为冲击激励所需重物质量的123倍。比较图4、图5可知，两条加速度时程曲线的相位角相差π/2。

2.3 参数分析

根据式(16)、式(17)可知，重物质量、坠落高度、绳索弹性模量、绳索截面积和等效振动系统的阻尼比是影响冲击力时程，进而影响最大加速度幅值的主要参数。应当考察这些参数对最大加速度幅值的影响。

假设绳索的弹性模量为E=1.0×1011N/m2，绳索截面积为A2=100 mm2，阻尼比为ζ=0.05。在1～10 kg内变化重物质量M，并取坠落高度s1变化范围为0.5～3.0 m。将不同参数组合下计算得到的冲击力时程施加于结构，并拾取结构的最大加速度幅值绘于图6。不难发现，对于不同的坠落高度，最大加速度幅值与重物质量基本呈线性关系。重物质量越大，最大加速度幅值也越大。同时，坠落高度越大，直线的斜率越大。

图3 冲击力时程

图4 冲击激励下最大加速度幅值对应的自由度加速度时程

图5 阶跃激励下最大加速度幅值对应的自由度加速度时程

假设重物质量为M=5 kg，坠落高度为s1=2 m，阻尼比为ζ=0.05。在0.25×1011～2.00×1011N/m2内变化绳索弹性模量E，并取绳索截面积A2变化范围为50～300 mm2。将不同参数组合下计算得到的冲击力时程施加于结构，并拾取结构的最大加速度幅值绘于图7。由图7可知，对于不同的绳索截面积，最大加速度幅值与绳索弹性模量的关系曲线均具有一定波动性，且变化非常平缓。可见，最大加速度幅值对绳索弹性模量的变化并不敏感。相比之下，当其他参数固定时，绳索截面积越大，最大加速度幅值也越大。

假设重物质量为M=5 kg，绳索弹性模量为E=1.00×1011N/m2，绳索截面积为A2=100 mm2。在0.01～0.10内变化等效振动系统的阻尼比ζ，并取坠落高度s1变化范围为0.5～3.0 m。将不同参数组合下计算得到的冲击力时程施加于结构，并拾取结构的最大加速度幅值绘于图8。由图8可知，对于不同的坠落高度，最大加速度幅值大致随阻尼比的增大而减小，但变化较为缓慢。可见，最大加速度幅值对阻尼比的变化并不敏感。当其他参数固定时，坠落高度越大，最大加速度幅值也越大。

从图6～图8综合判断，结构的最大加速度幅值对重物质量、坠落高度和绳索截面积较为敏感，对绳索弹性模量和等效振动系统的阻尼比不敏感。因此，较大的重物质量、坠落高度和绳索截面积有利于结构产生较大的加速度幅值。

根据杜哈梅积分，结构的加速度响应由结构动力特性和冲击力时程共同决定。由于算例中结构动力特性是固定的，各节点竖向刚度(即k1)差异不大(变化范围为4.082 9× 107～1.415 8×108kN/m)，而其他所考察参数的变化范围较大，因此可以定性判断，即使选取其他节点作为激励点，算例中结构最大加速度幅值对各参数的敏感性也不会有太大变化。

但是，若以其他结构(如不同类型和不同跨度的网架、网壳等)作为分析对象，则由于动力特性不同以及各节点竖向刚度可能存在较大差异，结构最大加速度幅值对各参数的敏感性值得进一步考察。

图6 重物质量和坠落高度对最大加速度幅值的影响

图7 绳索弹性模量和截面积对最大加速度幅值的影响

图8 等效振动系统阻尼比对最大加速度幅值的影响

2.4 与阶跃激励的比较

假设绳索的弹性模量为E=1.0×1011N/m2、绳索截面积为A2=100 mm2、等效振动系统的阻尼比为ζ=0.05。在1～10 kg内变化重物质量M，并取坠落高度s1变化范围为0.5～3.0 m。将不同参数组合下计算得到的冲击力时程施加于结构，并拾取结构的最大加速度幅值列于表2。表2中还列出了阶跃激励产生相同最大加速度幅值所需的重物质量。以表3中第1行第1列数据(1.22, 93)为例来说明表中数据的含义。该数据表示当重物质量为1 kg、坠落高度为0.5 m时，冲击激励产生的最大加速度幅值为1.22 m/s2，阶跃激励产生相同最大加速度幅值所需的重物质量为93 kg。由表2可知，为了产生相同的最大加速度幅值，阶跃激励所需的重物质量远高于冲击激励(表2中介于83.2倍～356.0倍)。

表2 冲击激励与阶跃激励所需重物质量的比较

3 结 论

以网架结构为例，提出一种基于重物坠落的冲击激励新方法。算例表明，所分析的网架结构最大加速度幅值对重物质量、坠落高度和绳索截面积较为敏感，对绳索弹性模量和等效振动系统阻尼比不敏感。与阶跃激励相比，冲击激励所需的重物质量大为减少，这有利于提高网架结构的动力测试效率、降低测试成本和获得具有较大信噪比的响应信号。本文工作为网架结构的主动激励提供了一种新的思路。在实际应用中，可以对等效振动系统的数学模型进行参数修正以考虑建模误差的影响。