柱状煤心瓦斯径向多尺度动态表观扩散模型与实验

2022-08-16李志强王海屿郝晓强李鹏飞

煤矿安全 2022年8期

李志强，王海屿，陈啸，郝晓强，李鹏飞

（1.河南理工大学煤矿灾害预防与抢险救灾教育部工程研究中心，河南焦作 454000；2.煤炭安全生产与清洁高效利用省部共建协同创新中心，河南焦作 454000；3.河南理工大学中原经济区煤层（页岩）气河南省协同创新中心，河南焦作 454000）

远距离超长钻孔抽采瓦斯是一种先进的区域瓦斯抽采技术，该措施具有抽采覆盖范围广，钻机移位次数少，抽采位置精准的优点，在我国大型矿井得到普遍应用。措施后的抽采效果检验是该技术的重要一环，抽采后的残余瓦斯含量大小是判断该区域抽采措施达标效果的重要指标。因而，深钻瓦斯含量准确测定成为远距离区域抽采效果检验的迫切需求。

大尺度柱状煤心因尺寸较大，具有瓦斯损失量小，残存量大等优势，且能实现定点取样，因而成为瓦斯含量测定的首选。另外，大尺度柱状煤心保留了更多的孔裂隙特征，接近于原始煤体的形态，可在测定瓦斯含量的同时，利用同组解吸流动数据计算无应力下煤体的本征渗透率，克服了颗粒煤无法代表原始煤体的弊端。然而，由于其形状和尺度已不同于颗粒煤，其解吸流动特征和理论模型也完全不同于颗粒煤，急需开展柱状煤心瓦斯的解吸流动实验与理论研究。

目前，关于瓦斯扩散大多采用颗粒煤进行实验研究。1951 年Barrer[1]在研究天然气在沸石中的流动时，导出了球状经典扩散模型的精确解。1975 年Crank[2]也得到了扩散率的精确解及简化式，该简化式即为法，由美国矿业局首先使用，随后被我国引入，并一直沿用至今。多年的使用表明，该模型仅适合描述煤体前10 min 的瓦斯解吸，而在使用此后的数据推算损失量时，不够精确。1971 年Ruckenstein[3]提出了双孔隙扩散模型，但计算较为复杂，不方便现场应用。1986 年，杨其銮等[4]在我国率先开展了解吸-扩散理论研究，在推导经典球状模型的基础上，提出了一个较为精确的经验扩散模型，用于分析粒径、压力、煤种对扩散的影响，已经成为研究瓦斯扩散的经典理论。1997—2001 年，郭勇义、聂百胜等[5-7]建立第3 类边界条件下煤粒瓦斯扩散模型，适用于描述颗粒煤中瓦斯流动。2016 年，李志强等[8-9]发现了煤中瓦斯扩散系数的动态衰减特征，提出了多尺度动扩散系数新模型，相比常扩散系数模型，该模型能够精确描述颗粒煤中瓦斯的全时扩散过程。随着颗粒煤中动态扩散系数的发现，此后的研究者们[10-13]发展了不同形式的动态扩散系数模型，大都是关于颗粒煤的球状模型。球状模型并不能展现柱状煤心瓦斯扩散特性，而关于柱状模型研究较少。例如，张淑同[14]对5 类煤样进行了解吸实验，证明Ⅰ、Ⅱ柱状煤心解吸速度较慢。因此，采用柱状煤心测定瓦斯含量时损失量较少，瓦斯含量测试精度有所提高。Pan Z 等[15]和Tan 等[16]分别采用柱状煤心和块状煤进行了瓦斯扩散实验，利用球状双孔隙模型分析了煤样中瓦斯的扩散特征。李志强等[17]进行柱状煤心扩散实验，建立了柱状煤心瓦斯常系数径向扩散方程，分析了其流动特征。然而，随着测试时间的延长，常系数扩散模型误差逐渐增大。

综上，目前关于柱状煤心瓦斯径向流动方面的模型尚不精确，极大的影响了长钻孔瓦斯含量的精度，也影响了无应力下原煤本征渗透率的准确测定。因此，亟需对柱状煤心瓦斯径向流动进行进一步的实验和理论研究。为此，开展柱状煤心瓦斯径向解吸-扩散实验，建立了径向多尺度动态表观扩散模型，以期为深钻瓦斯含量测定和本征渗透率的研究提供一种相对精确的理论模型。

1 柱状煤心瓦斯扩散实验

1.1 实验方法

1）煤样制备。实验煤样取自河南焦作赵固矿，在原煤块体上垂直层理钻取规格为ϕ50 mm×100 mm标准圆柱状煤心，为保证柱状煤心瓦斯沿径向扩散，将煤心两端面进行胶封。同时取原煤块的一部分粉碎成1～3 mm 的颗粒状煤样，以做对比实验。其余煤样按GB/T 212—2008《煤的工业分析方法》测定煤的水分、灰分、挥发分，同时测定煤的密度和孔隙率，按高压容量法测定煤样吸附常数a、b 值。煤样的基本参数见表1。

表1 煤样的基本参数Table 1 Basic parameters of coal samples

2）实验仪器。采用自主研制的煤瓦斯扩散实验系统开展实验，该设备包括充气单元、真空抽气单元、瓦斯吸附平衡单元和瓦斯解吸测量单元4 个部分。柱状煤心-瓦斯扩散实验系统如图1。其中，充气单元由甲烷气瓶、阀门V1、阀门V2、减压阀和压力表组成；抽真空单元由真空泵及阀门V3 构成；瓦斯吸附平衡单元由瓦斯扩散仪、阀门V4～V6 组成，V6为放空阀。瓦斯解吸测量由阀门V7 和解吸测量仪构成。

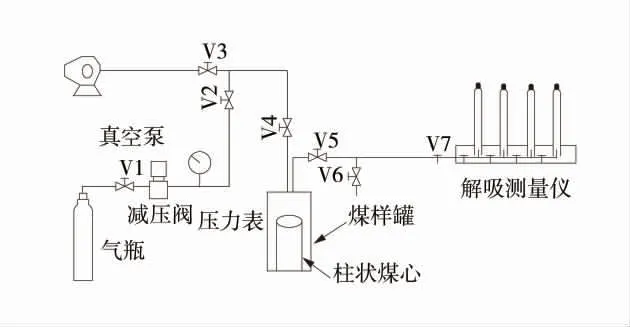
图1 柱状煤心-瓦斯扩散实验系统Fig.1 Diffusion testing system for cylindrical coal

3）煤样真空脱气。将柱状煤样置于煤样罐中，关闭阀门V1、V2、V5、V6、V7，并打开阀门V3、V4，开启真空泵对煤样罐以及管路进行抽真空，排除杂质气体以及水分，当真空压力达到10 Pa 时，关闭真空泵停止脱气，同时关闭阀门V3。

4）瓦斯吸附-解吸实验过程。首先，打开甲烷气瓶及阀门V1、V2，关闭阀门V3，设定初始气压0.5 MPa，对煤样罐内的柱状煤样充气。吸附数天达到平衡后，关闭阀门V4，打开阀门V5、V6 放出管内高压气体，5 s 后关闭阀门V6，打开阀门V7，使煤中瓦斯解吸180 min，通过解吸测量仪，测量累计解吸量。直至180 min 后累计解吸量变化很小，结束测试。依次改变气压为0.5、1、2、3 MPa，重复上述操作步骤。

1.2 实验数据的处理方法

式中：p 为初始吸附平衡压力；Aad为灰分，%；ϕ为孔隙率，%；ρ 为视密度，g/cm3；θw为解吸仪水温。

2 实验结果

2.1 不同气压下的扩散比率

根据式（1）和实验测定的某时刻下的累积解吸量Qt，计算绘制出扩散比率Qt/Q∞与时间t 的变化曲线，不同吸附平衡压力下的扩散比率如图2。

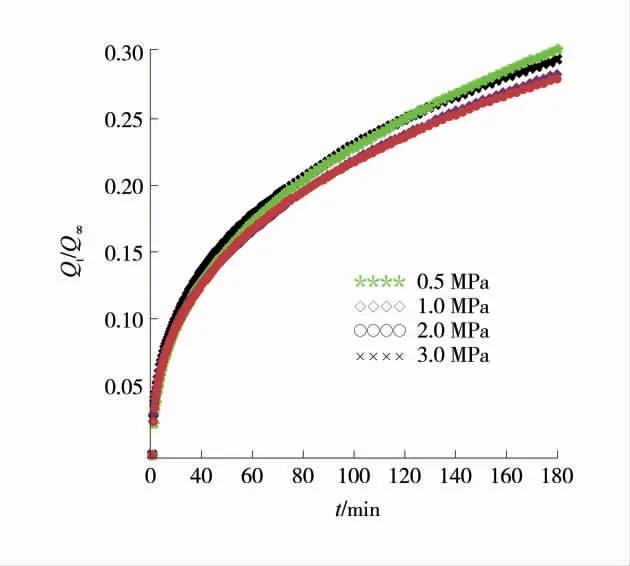
图2 不同吸附平衡压力下的扩散比率Fig.2 Diffusion ratios under different adsorption pressures

2.2 扩散实验的经典扩散模型

柱状煤经典径向扩散方程的解析解为[17]：1 个正根与R 的比值。

以图2 中0.5 MPa 的实验点为例进行计算，0.5 MPa 气压下柱状煤径向扩散实验的参数拟合曲线如图3。

由图3 可知，曲线斜率λ 随时间延长而减小，即扩散系数D 也随时间延长而衰减。而经典模型假定扩散系数D 为常数，因而按经典模型计算的趋势线(图3 中直线)与实验曲线严重偏离。根据图3 计算出λ=0.001 47，将λ 代入式（2）进行计算，0.5 MPa气压下柱煤径向扩散实验与经典扩散模型拟合曲线如图4。

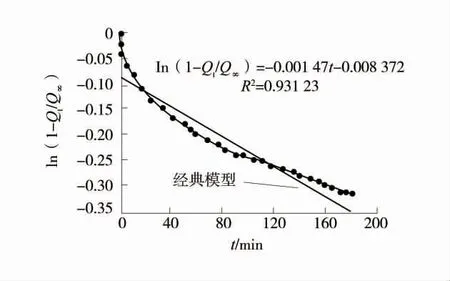
图3 0.5 MPa 气压下柱状煤径向扩散实验的参数拟合曲线Fig.3 Radial diffusion experiment and parameter fitting curves of columnar coal under 0.5 MPa pressure

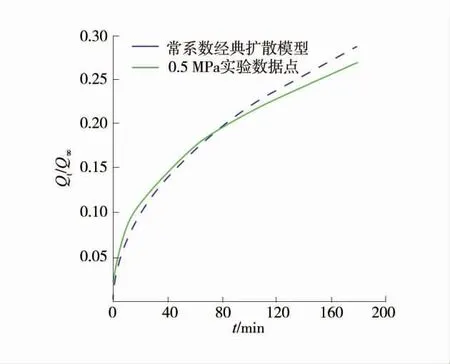
图4 0.5 MPa 气压下柱煤径向扩散实验经典扩散模型拟合曲线Fig.4 Fitting curves between radial diffusion experiment classical diffusion model of pillar coal under 0.5 MPa pressure

由图4 可知，在t=90 min 时，实验曲线与理论曲线出现交叉；在t=90 min 之前，扩散比率的实验值大于理论值；而t=90 min 后，实验值小于理论值，实验值与理论值出现较大偏差，经典模型不能描述柱状煤中瓦斯扩散全过程。导致偏差的原因为：扩散系数随时间的延长而衰减，而经典模型将扩散系数假定为常数。

3 多尺度动态表观动态扩散模型

3.1 动态表观扩散系数的约定

煤中孔隙大小不一，包含了微孔、小孔、中孔、大孔，可见孔及裂隙，尺度由几纳米至几毫米不等。目前，大部分研究学者认为，瓦斯在裂隙以及大孔隙中为渗流，由压力驱动，在基质微孔中为扩散，由浓度驱动。然而，即使在极小粒径的煤样中，仍然存在着裂隙。因而，目前尚无法对渗流和扩散的孔隙大小进行区分。对于柱状煤心的瓦斯解吸过程而言，扩散和渗流2 种流动方式均存在。无论是扩散方程或者渗流方程，2 种方程均属于数学物理方程中数学意义上的扩散方程。又因为在进行实验时，瓦斯累计扩散量更加容易测定，而且根据实验结果进行质扩散方程计算要比渗流方程容易的多。然而，在物理意义上，质扩散方程计算的结果，包括了渗流和扩散2 种流动方式，因此应将该扩散系数定义为表观扩散系数，即实验表象意义上的扩散系数。

为了提高理论计算的准确性，一些学者根据孔隙的大小，建立了大孔和微孔2 个偏微分方程，即双孔隙模型，但计算过程复杂。因此，为规避双孔隙模型的复杂性，选择以扩散系数与时间的关系来建模。结合2.2 中扩散系数随时间的变化逐渐衰减的实验关系，假定扩散系数与时间呈负指数关系，即：

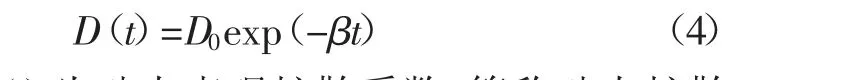
式中：D（t）为动态表观扩散系数，简称动态扩散系数，cm2/s；D0为初始表观扩散系数，cm2/s；β 为动态表观扩散系数的衰减系数，s-1。

3.2 动态表观扩散数学模型

动态表观扩散模型的基本假设如下：①柱状煤心的径向尺寸小于轴向尺寸，由于层理的各向异性效应，径向流动阻力小于轴向，瓦斯主要从径向流出；②假设柱状煤心为非均质，并假设柱状煤心的扩散系数与时间呈负指数动态关系，仅在数学意义和实验意义上，将扩散系数定义为表观扩散系数，避免物理意义上扩散与渗流的区分困难，模型和实验中假设渗流与扩散同时存在，表观扩散系数即包含了渗透率和扩散系数2 类参数；③煤心及瓦斯在平面内均为连续介质，根据实验条件，出口边界的质量浓度为定值。

柱状煤心瓦斯径向流动的连续性质量守恒方程如下：

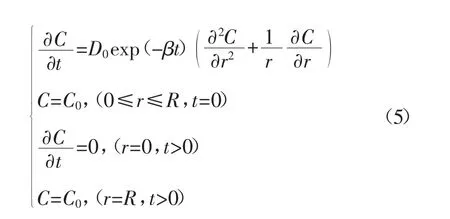
式中：C 为柱状煤心中瓦斯质量浓度，cm3/g；r为扩散路径，cm；C0为吸附平衡时的初始质量浓度，cm3/g；Ca为扩散过程中柱状煤心表面的瓦斯质量浓度，cm3/g。

采用分离变量法求解式（5），得到：

式中：Mt为某时刻下的累积解吸量；M∞为实际极限解吸流动量。

比较式（2）和式（6）可以看出，经典模型式（2）中的表观扩散系数D 是式（6）中动态表观扩散系数D（t）在0～t 时段内的积分平均值。

3.3 动态表观扩散模型的实验验证

将柱状煤心瓦斯径向解吸流动实验数据分别按式（2）和式（6）进行处理，不同气压下柱状煤径向扩散实验与2 类模型的拟合曲线如图5。

图5 不同气压下柱状煤径向扩散实验与2 类模型的拟合曲线Fig.5 Comparison between fitting curves of two model and cylindrical diffusion experiments under different gas pressures

由图5 可知，常系数经典扩散模型不能精确描述扩散实验全过程。在90 min 前，实验值大于理论值；而90 min 后，实验值小于理论值，表明表观扩散系数在随时间延长而衰减。采用动态表观扩散模型式（6）计算后，新模型的理论曲线与实验曲线近乎重合，表明新模型能够精确描述柱状煤心瓦斯的径向流动全过程。

3.4 柱状煤心瓦斯表观扩散特征

表观扩散系数是反映扩散-渗流特征的最本质的科学参数。为此，用动态表观扩散模型和经典模型分别计算出相应的表观扩散系数，不同压力下的扩散参数见表2。

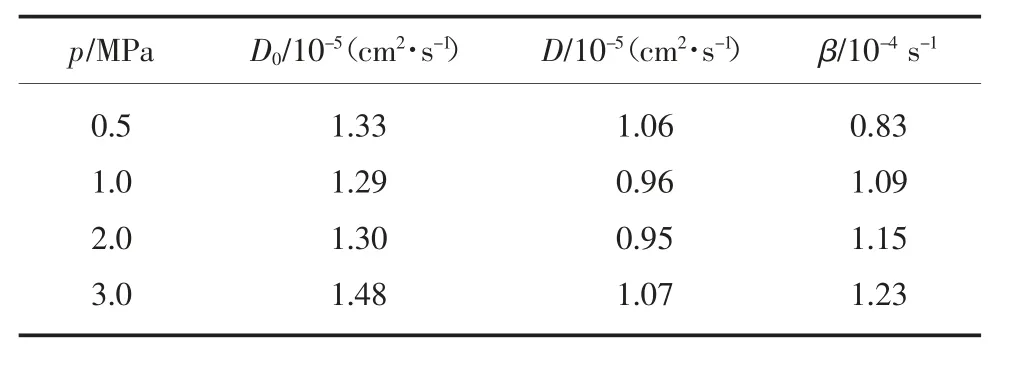
表2 不同压力下的扩散参数Table 2 Diffusion parameters under different pressures

从表2 中看出，动态扩散模型的D0值始终大于经典模型的D 值。当气压增大时，无论是D0值还是D 值均表现出先减小后增大的“U”型趋势，而β 随气压增大而增大。β 代表了煤体的孔隙间的孔径级差特征，其值越大，表明孔隙的孔径差越大。D0与β值综合表达了煤体孔隙及相应的表观扩散系数的多尺度特征。流动初期，瓦斯首先从大孔隙中流出，此时的表观扩散系数较大，流动后期，瓦斯从小孔隙中流出，此时表观扩散系数较小，随着时间的延长，流经的孔隙孔径逐级变小，导致表观扩散系数随时间延长而衰减。

从图5 可以看出，4 个压力下的扩散比率基本接近，30 min 的解吸比率仅为13.5%，60 min 的比率为16.4%，90 min 的比率为19.5%，120 min 的比率为21.7%，180 min 的比率为26.2%。为了更加明显的观察柱状煤心瓦斯的扩散特征，压力1.0 MPa 下，将柱状煤心与颗粒煤（1～3 mm）的扩散比率进行比较，柱状煤心与颗粒煤的扩散比率如图6。

图6 柱状煤心与颗粒煤的扩散比率Fig.6 Comparison of diffusion ratio between cylindrical and particle coal

由图6 可知，同一时刻下，柱状煤心的扩散比率远远小于颗粒煤。进一步计算表明，颗粒煤的D0为8.35×10-7cm2/s，β 值为2.1×10-4s-1，远小于柱状煤心的D0值，这是因为柱状煤包含了更多的大裂隙孔隙，导致柱状煤心有更大的渗透能力。但同时，柱状煤心的径向半径为2.5 cm，而颗粒煤的球向半径为0.037 5 cm，柱状煤的流动路径远远大于颗粒煤，因而在宏观上，柱状煤心扩散比率远小于颗粒煤。

柱状煤心这种表观扩散特征在工程应用上具有重要意义。因其瓦斯释放能力弱，所以初始阶段瓦斯损失量小，可以有效提高预测瓦斯含量的准确性。尤其对于深钻取心测定含量而言，由于取心耗时较长，柱状煤心的这种扩散特征，恰好可以弥补取心时间长的缺陷，极大的减少损失量。同时，新模型能准确描述瓦斯全过程，即使有部分损失，也可以利用高精度的理论计算准确的推算出损失量。值得注意的是，由于煤种不同，代表流动能力的表观扩散系数不同，一些扩散能力弱的煤体，5 h 内损失比率不足10%，对于深钻测定瓦斯含量具有更大的优势。