基于离散小波变换和变分自编码器的滚动轴承剩余使用寿命预测
2022-08-16孟祥龙丁华吕彦宝施瑞
孟祥龙,丁华,吕彦宝,施瑞
(1.太原理工大学 机械与运载工程学院,太原 030024;2.煤矿综采装备山西省重点实验室,太原 030024)
滚动轴承广泛应用于众多机械设备中,作为关键的承载部件,长期处于复杂、恶劣的工作环境中,具有故障率高,易损坏的特点,是机械故障的主要源头,因此轴承剩余使用寿命(Remaining Useful Life, RUL)预测对于机械设备的预测性维护有着重要意义[1]。精准地预测轴承剩余使用寿命,可以让机器以最小的维护成本来获得最长的安全运行时间,进而提升机器运行过程中的安全性和经济性。
人工智能的发展使数据驱动的轴承健康监测维护[2]相比传统方法更具优越性,基于数据驱动的轴承剩余寿命预测主要分2步:1)从采集的振动加速度信号中提取轴承性能退化特征;2)构建预测模型,利用机器学习或深度学习卓越的非线性映射能力寻找数据特征与剩余使用寿命之间的潜在关系[3]。特征提取是数据驱动方法的重要步骤,其关键在于从监测数据中挖掘机械设备运行状态信息,对剩余使用寿命预测精度有很大影响。传统特征提取方法是从原始振动信号中提取退化特征,如提取时域的均方根值、频域的平均幅值以及时频域的小波包能量谱等[4];文献[5]则利用卷积神经网络特有的局部卷积、权值共享等特性直接对原始信号进行特征自学习,省去了专家先验知识,实现了端对端的剩余使用寿命预测。然而,原始信号中含有大量噪声,轴承的退化特征极易被噪声淹没,影响剩余使用寿命预测精度。当从不同分析域中提取特征指标后,很难判断其中哪些特征对轴承缺陷发展更加敏感[6];并且这些特征仍是高维,需要通过降维融合剔除冗余信息,获得能全面反应轴承性能退化趋势的综合指标。文献[7]利用主成分分析从多维数据中获取优势信息的特性来实现特征的融合降维,文献[8]采用自编码器构建了低维性能退化指标;然而,主成分分析处理线性问题具有优势,却难以充分挖掘轴承变化的有效信息;自编码器是将高维数据映射为低维特定数值[9]而不是某种分布,得到的低维特征受到约束,退化趋势较单一。
针对以上问题,本文提出一种基于离散小波变换(Discrete Wavelet Transform,DWT)和变分自编码器(Variational Auto-Encoder,VAE)的滚动轴承剩余使用寿命预测方法。通过离散小波变换对轴承振动信号进行逐级分解以抑制信号中的环境噪声和无关成分,从而选取有效信息成分多、噪声成分少的分量作为后续算法处理的对象,实现降噪预处理的效果;同时,利用变分自编码器强大的无监督特征学习能力和抗干扰能力获得更符合轴承退化趋势的综合特征;最后,通过分层抽样划分数据集,并引入长短时记忆(Long Short-Term Memory,LSTM)网络实现滚动轴承剩余使用寿命预测。
1 基于DWT和VAE的轴承寿命预测
1.1 离散小波变换
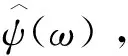
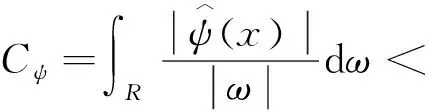
(1)
则称为一个基本小波或母小波,将母函数ψ(t)经伸缩和平移后,可以得到一个小波序列。
对于连续的情况,小波序列为
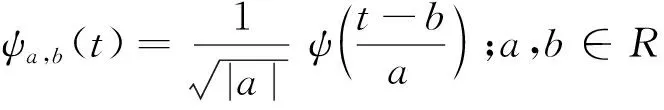
(2)
连续小波变换为
(3)
式中:a为伸缩因子;b为平移因子。
对于离散的情况,小波序列为
(4)
通常取a0=2,b0=1,则 (4) 式变为
(5)
3层离散小波变换的原理如图1所示,其中H(w)为低通滤波器,可以滤除曲线中的高频部分,得到近似部分(低频成分);G(w)为高通滤波器,可以滤除曲线中的低频部分,得到细节成分(高频成分);从而将信号的时频结构准确无冗余地展现出来。

图1 3层离散小波变换原理示意图
1.2 变分自编码器
变分自编码器是一种基于自编码器的无监督学习方法,同时也是一种生成模型,通过编码器获得潜在空间特征的概率分布,融入随机噪声并以解码器的形式生成新数据,其基本结构如图2所示。与自编码器直接将输入x映射到隐含向量z不同,变分自编码器的编码部分是将输入x映射到隐变量概率分布的参数(均值、方差),再加入随机噪声后采样得到隐变量z,最后由解码部分生成新的数据。
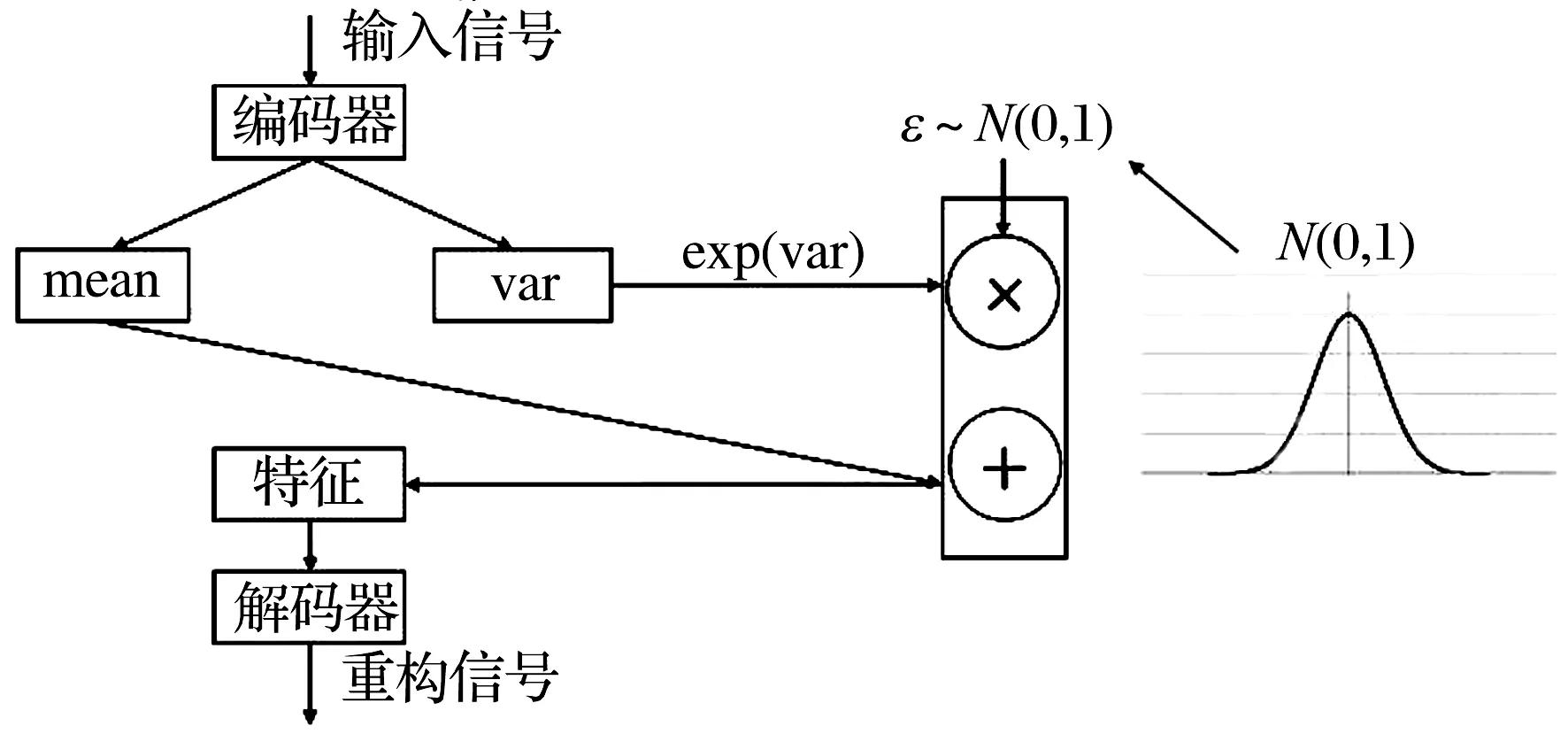
图2 变分自编码器基本结构
变分自编码器包含编码器、解码器和损失函数3部分。编码器是一个神经网络,输入为x,输出为隐向量z,参数为θ,可表示为pθ(z∣x);解码器也是一个神经网络,输入为隐向量z,输出为重构的x,参数为φ,可表示为qφ(x∣z);损失函数为
L(θ,φ)=Ez~pθ(z∣x)[lgqφ(x∣z)]+
DKL[pθ(z∣x)p(z)],
(6)
等式右侧第1项为重构损失,与其他自编码器的损失函数一样,目的是让生成数据与原始数据尽可能相近;第2项为KL 散度(相对熵),是正则项,用来衡量2种不同概率分布之间的偏离程度。
在变分自编码器中,隐空间先验分布p(z)被设定为标准正态分布,正则项的存在是要让后验分布pθ(z∣x)也接近先验分布。如果没有正则项,模型为了减小重构损失会不断减小随机性,也就是编码器输出的方差,没有随机性时,变分自编码器无法生成各种数据。若编码器输出的z不服从标准正态分布,将会在损失函数中对编码器施加惩罚。
变分自编码器中,pθ(z∣x)确定一个高斯分布并从中采样得到隐变量z,然而采样操作的不可导使模型无法反向传播。在实际模型中,采用重参数技巧解决后验分布采样过程中梯度不可计算的问题,即从均值μ和标准偏差σ的正态分布中采样,等价于先从标准正态分布中采样,然后再对其进行变换,即
z=μ+σ⊙,
(7)
1.3 剩余使用寿命标签设定
在实际应用中,轴承运行前期振动信号的振幅十分平稳,可视为健康运行阶段。轴承运行一段时间后,在某一时刻发生初始故障,标志着轴承开始进入退化阶段,轴承振动信号振幅不再趋于平稳而是剧烈振荡且伴随着轴承性能的急剧下降,直至轴承失效,如图3a所示。由于轴承在健康阶段并没有出现一定的退化演变趋势,使用图3b中线性剩余使用寿命标签进行剩余使用寿命预测时效果较差。因此,在轴承运行健康阶段,将剩余使用寿命设定为一个常数值较为合理[10],直到出现初始故障,轴承开始进入退化阶段,剩余使用寿命才开始逐渐减小,可以采用分段函数表示[11],如图3b中虚线所示。

(a)原始振动信号
1.4 模型介绍
长短时记忆网络是循环神经网络的一个变体,可以有效地解决循环神经网络的梯度爆炸或消失问题,其在循环神经网络的基础上引入门控机制控制信息的累积速度,包括有选择地加入新信息,有选择地遗忘之前累积的信息。长短时记忆网络的具体公式为
it=σ(Wxixt+Whiht-1+bi),
(8)
ft=σ(Wxfxt+Whfht-1+bf),
(9)
ot=σ(Wxoxt+Whoht-1+bo),
(10)
ct=ft⊙ct-1+it⊙tanh(Wxcxt+Whcht-1=bc),
(11)
ht=ot⊙tanh(ct),
(12)
式中:it,ft,ot分别为输入门、遗忘门和输出门;c,h分别为记忆单元和外部状态;σ为 Logistic函数,输出区间为(0,1);W为各神经元的权重,其与输入矢量xt和外部状态ht-1直接点乘。
长短时记忆网络的循环单元结构如图4所示,其计算过程为:1)利用上一时刻的外部状态ht-1和当前时刻的输入xt,计算出3个门it,ft,ot以及候选状态ct;2)结合遗忘门ft和输入门it更新记忆单元ct;3)结合输出门ot将内部状态的信息传递给外部状态ht。通过长短时记忆网络循环单元,整个网络可以建立较长距离的时序依赖关系。
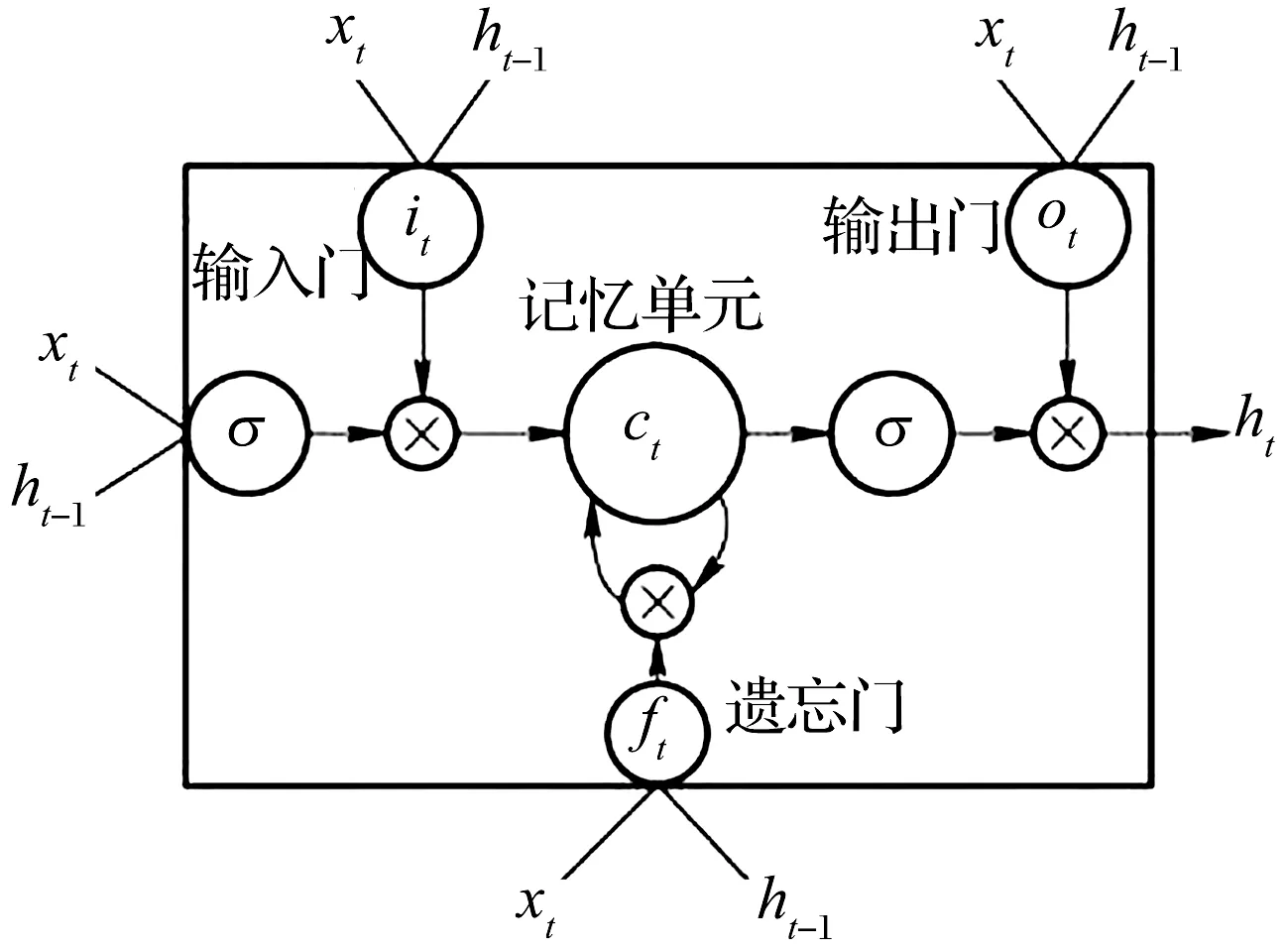
图4 长短时记忆网络结构示意图
2 实例验证
2.1 数据来源
试验数据来自美国辛辛那提大学IMS中心轴承试验台[12],试验轴承为 ZA-2115型滚动轴承,轴转速为 2 000 r/min,由弹簧机构施加 26.67 kN 的径向力加速轴承退化,采用高灵敏度PCB-353B33加速度传感器收集轴承振动信号,采样频率为20.48 kHz,采样间隔为10 min,采样时间1 s,故每次采样点数为20 480。选择第2组试验中轴承1的全寿命周期振动数据进行分析,其在历时9 840 min后发生疲劳失效(拆机发现外圈出现裂纹),其振动信号在后期产生剧烈变化,反映出轴承发生了急剧退化。
2.2 试验结果分析
首先需要确定轴承初始故障发生的时刻,并以此作为初始退化点来划分轴承运行的健康阶段和退化阶段。由于轴承早期故障特征难以检测,致使初始退化点难以确定,采用文献[13]中所提方法进行初始退化点检测。轴承发生故障时会在其频谱中有所体现,可以利用频谱中最大峰值频率的改变找出初始退化发生的时刻。将每次采样得到的振动信号进行快速傅里叶变换得到频谱,把频谱中幅值最大的频率记录下来,得到的散点图如图5所示:轴承运行前期只存在1 000 Hz的频率,随着轴承持续运行,第7 000 min以后开始持续出现4 476 Hz的故障频率,故将第7 000 min确定为轴承的初始退化时刻。
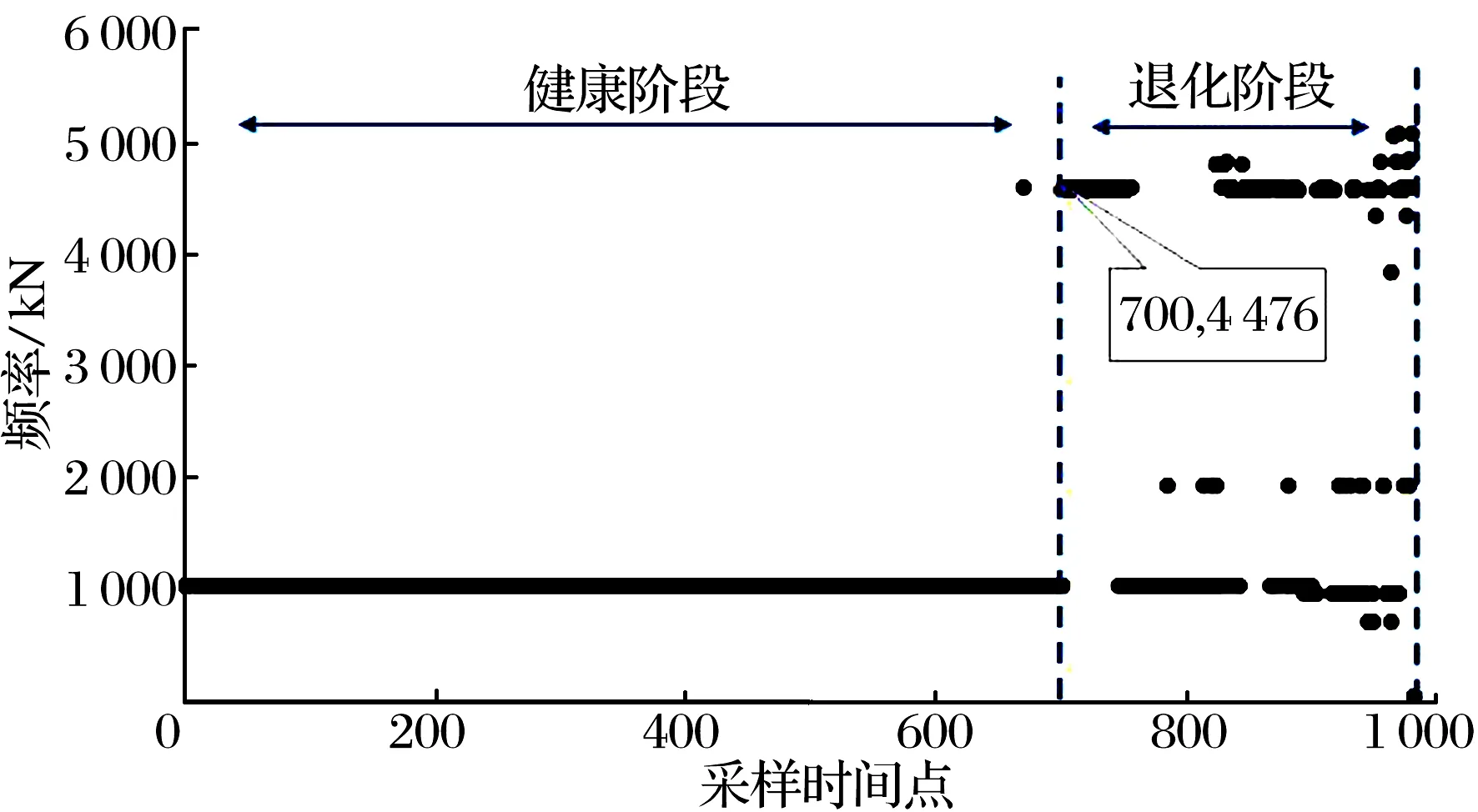
图5 初始退化点检测
分段函数将0~7 000 min视为健康状态,归一化后RUL标签为1;第7 000 min之后视为退化状态,其标签值递减直至为0,表征轴承损坏已达阈值,无法再正常运行,如图6所示。
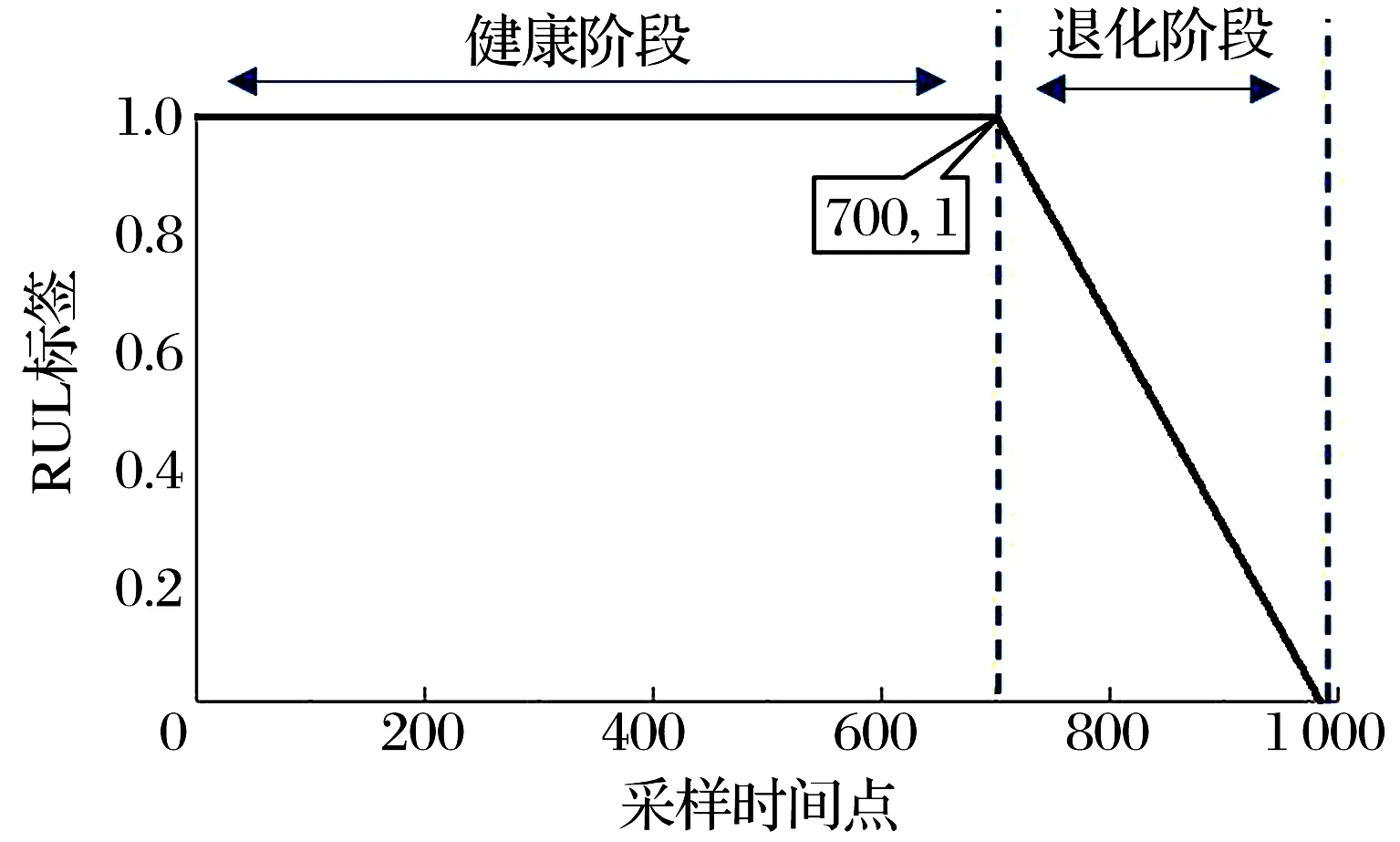
图6 归一化分段函数RUL标签
在特征提取方面。考虑到db小波基函数具有正交性、紧支撑性以及对不规则信号更敏感等特性,选择db4小波作为基函数,将轴承原始振动信号进行3层离散小波变换处理,得到近似分量信号和细节分量信号并从中分别提取标准差、方根幅值、均方根、偏度、峭度以及波形因子特征,结果如图7所示。
从图7中剔除对轴承退化趋势不敏感的偏度、峭度以及波形因子,选择单调趋势性较好的标准差、方根幅值和均方根作为敏感特征构建高维特征集,如图8所示:从近似分量中提取的均方根在退化阶段的单调上升趋势更符合指数型增长,其明显优于细节分量中提取的方根幅值;而从局部放大图中可以看出,近似分量的均方根在健康阶段非常平稳,而细节分量的方根幅值在健康阶段已有轻微的起伏上升,表明细节分量特征对于轴承的损坏更加敏感,能提取到轴承早期微弱的退化信息;因此,单单使用均方根或方根幅值无法完整表达轴承整个寿命周期的退化趋势,需要通过特征融合获得反映轴承退化的综合性能指标。
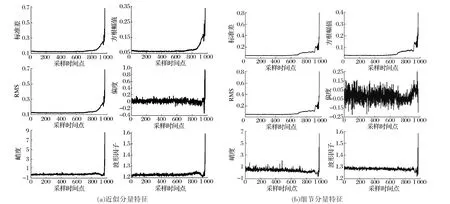
图7 离散小波变换处理后轴承振动信号的特征指标Fig.7 Feature indexes of bearing vibration signal after DWT processing
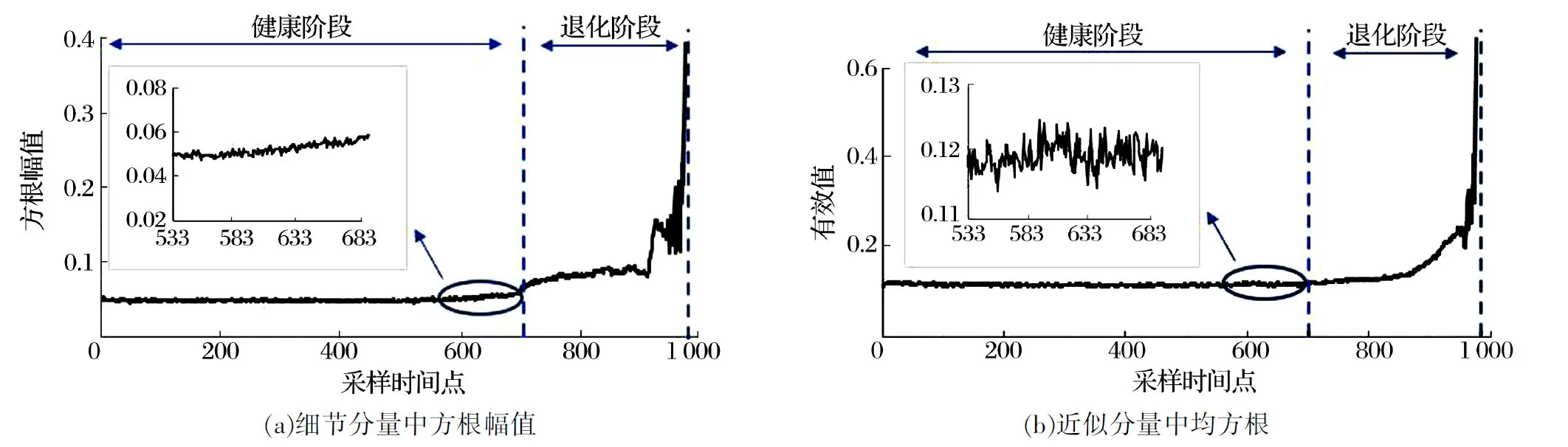
图8 离散小波变换处理后轴承振动信号的部分敏感特征
利用归一化操作对敏感特征构成的高维特征集进行缩放并输入变分自编码器中进行无监督特征融合降维,将高维特征集降至一维后所得轴承的深层本质特征如图9所示,其中x轴代表时间点,y轴代表将高维特征集输入到变分自编码器后融合降维得到的一维深层特征值。由图9可知:由

图9 变分自编码器降维得到的一维特征
离散小波变换和变分自编码器提取出的深层特征具有良好的单调性,既能体现健康阶段的轻微损伤(局部放大图),又能在退化阶段表现出良好的指数型单调上升,能够综合表征轴承整个生命周期的衰退过程,可以将其作为基本特征输入长短时记忆网络模型进行轴承剩余使用寿命预测。
试验轴承全寿命周期数据共有984个时间点,最后8个时刻的监控数据与实际趋势不一致,误差较大。为避免这一误差的影响,将这部分数据剔除。采用分层抽样的方法将全寿命周期数据划分为训练集和测试集[14],以10个时间点为一层,以7:3的比例对每一层数据进行随机抽样构建训练集和测试集,训练集和测试集分别占全寿命周期数据的70%和30%,最后得到训练集与测试集样本数的比为683:293。
长短时记忆网络模型重要的超参数有时间步长、隐藏层状态数、批量大小和学习率,超参数的选择会影响预测结果的精确性,因此采用粒子群优化算法(Particle Swarm Optimization,PSO) 对超参数进行设定,设置粒子群优化算法搜索空间的上、下界分别为[20,128,100,0.01],[2,8,10,0.000 1],种群数量为20,使模型预测效果达到最优的超参数为[10,70,32,0.005 3]。另外,由于Adam作为自适应优化算法能够动态更新学习率,因此选择Adam优化器进行梯度优化。
长短时记忆网络模型在测试集上的预测结果如图10所示,预测值与RUL标签有很高的重合度。为评估剩余使用寿命预测的不确定性,采用文献[15]方法对性能退化阶段进行区间估计,在预测值附近设置 95%置信水平的置信区间。虽然有些预测值偏离RUL标签曲线(局部放大图),但绝大部分预测值均落在置信区间内,说明预测值趋势与RUL标签曲线趋势一致。

图10 试验轴承在测试集上的RUL预测结果
2.3 对比试验
为验证方法的有效性,采用3种特征提取方法:1)直接从原始振动信号中提取时频特征;2)对原始信号进行小波软硬阈值折衷法去噪后[16]提取时频特征;3)对原始信号进行离散小波变换,对信号子分量提取敏感特征。融合降维则使用2种方法,即堆叠自编码器(Stacked Auto-Encoder,SAE)和变分自编码器。将3种特征提取方法与2种融合降维方法相互组合,共形成6种方法进行对比,其得到的一维特征如图11所示。
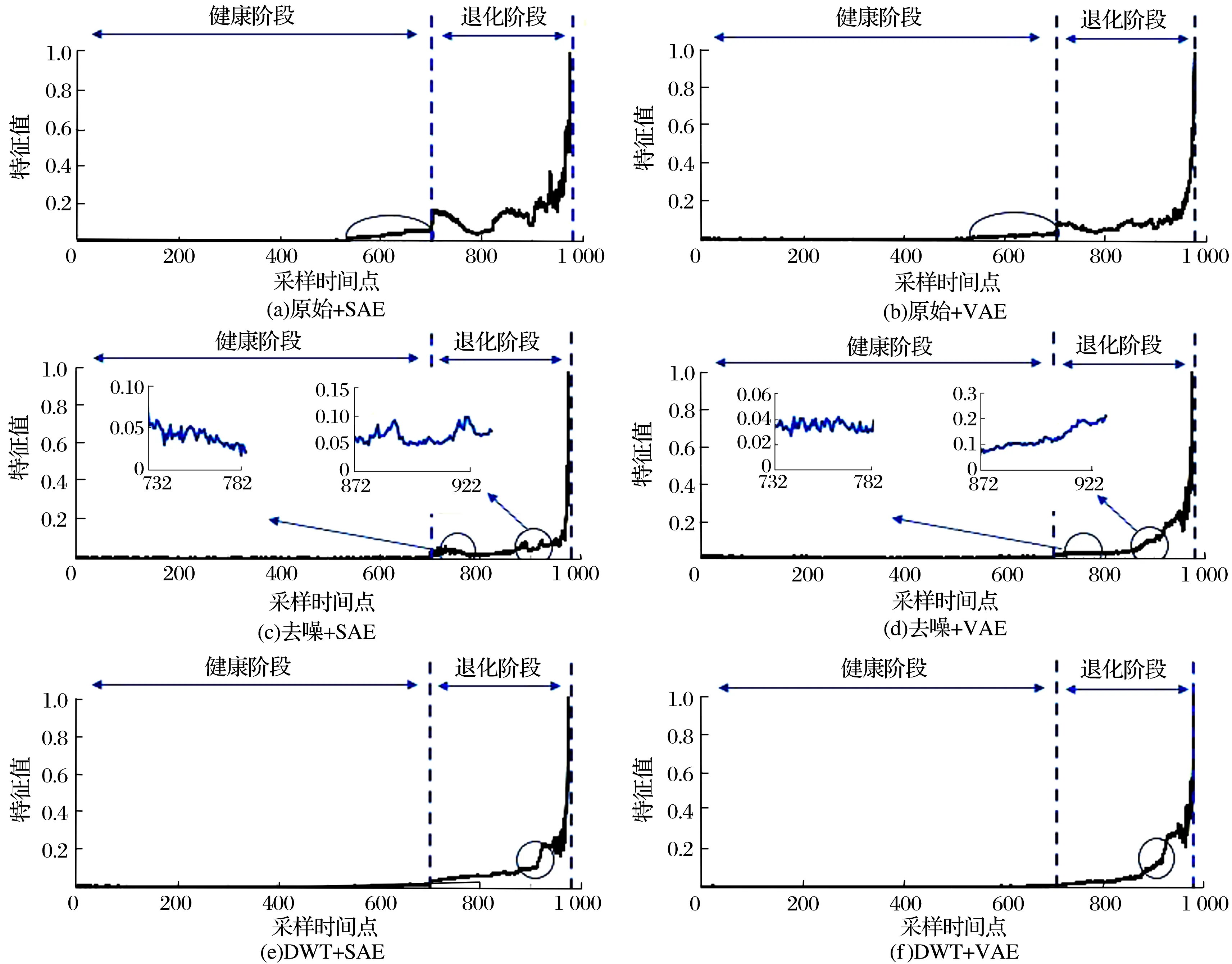
图11 不同特征提取和降维融合方法提取的一维深层特征Fig.11 One-dimensional deep features extracted by different eature extraction and dimension reduction fusion methods
由图11可知:1)原始信号深层特征在健康阶段起伏上升现象明显,而经过小波软硬阈值折衷法去噪和离散小波变换处理后所提取深层特征在健康阶段十分平稳,起伏上升得到大幅抑制,且离散小波变换所提取特征在退化阶段呈指数型上升,更符合轴承退化趋势,对轴承振动信号特征提取的效果更好;2)以小波去噪为例,堆叠自编码器提取的深层特征在退化阶段表现出先轻微下降再缓慢上升,即“愈合”现象,而变分自编码器提取的深层特征在退化阶段先趋于稳定再快速上升,退化趋势明显更优,说明相对于堆叠自编码器,变分自编码器的融合降维效果更佳,可以有效抑制退化阶段的“愈合”现象[17],获得单调性更优的特征指标。
从定量分析的角度,进一步对一维深层特征的趋势性、单调性和鲁棒性进行分析[18],其计算结果见表1,表明离散小波变换和变分自编码器算法所提取深层特征的综合性能更优。
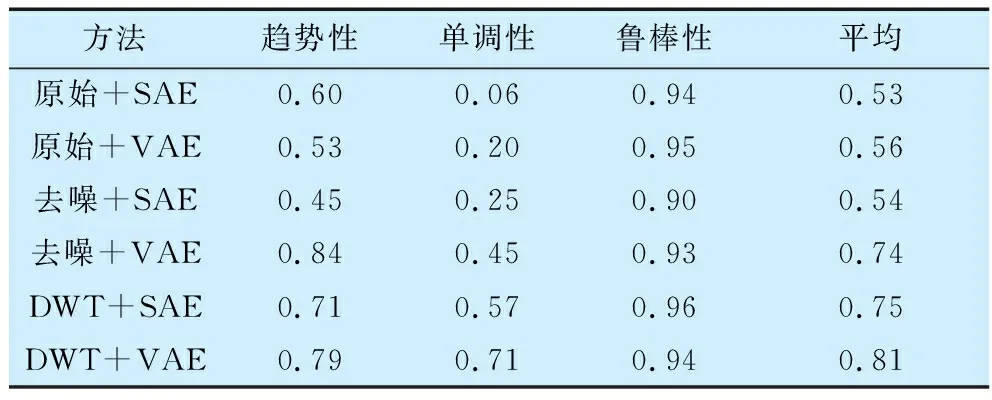
表1 不同方法所提取深层特征的定量评价指标
采用分层抽样对每种方法得到的深层特征划分训练集与测试集,通过训练集来训练长短时记忆网络模型,并使用测试集验证预测效果,结果如图12所示。

图12 不同方法所构建模型对试验轴承在测试集上的剩余使用寿命预测结果Fig.12 RUL prediction results of test bearing on test set by models constructed by different methods
选择能反映测量精度的均方根误差(Root Mean Square Error,RMSE)和能反映预测误差实际情况的平均绝对误差(Mean Absolute Error,MAE)作为模型的评价指标[19](表2),评价指标对应的计算公式为

表2 不同方法所构建预测模型的评价指标
(13)
(14)

分析图12和表2可以看出,基于离散小波变换和变分自编码器的滚动轴承剩余使用寿命预测方法的误差更小,精度更高。
2.4 不同初始退化点的预测结果
上述分析中,轴承初始退化点被确定为第7 000 min并以此划分健康阶段和退化阶段,然而文献[20]指出轴承在第5 330 min已发生轻微退化,到第7 000 min已是中度退化状态。因此,本文尝试分析不同初始退化点的选择是否会对所提方法产生影响,故将第5 330 min设定为初始退化点,则健康阶段为0~5 330 min,退化阶段为5 330~9 840 min。相应的分段函数如图13所示,其余处理与上述方法一致,得到的预测结果如图14所示。
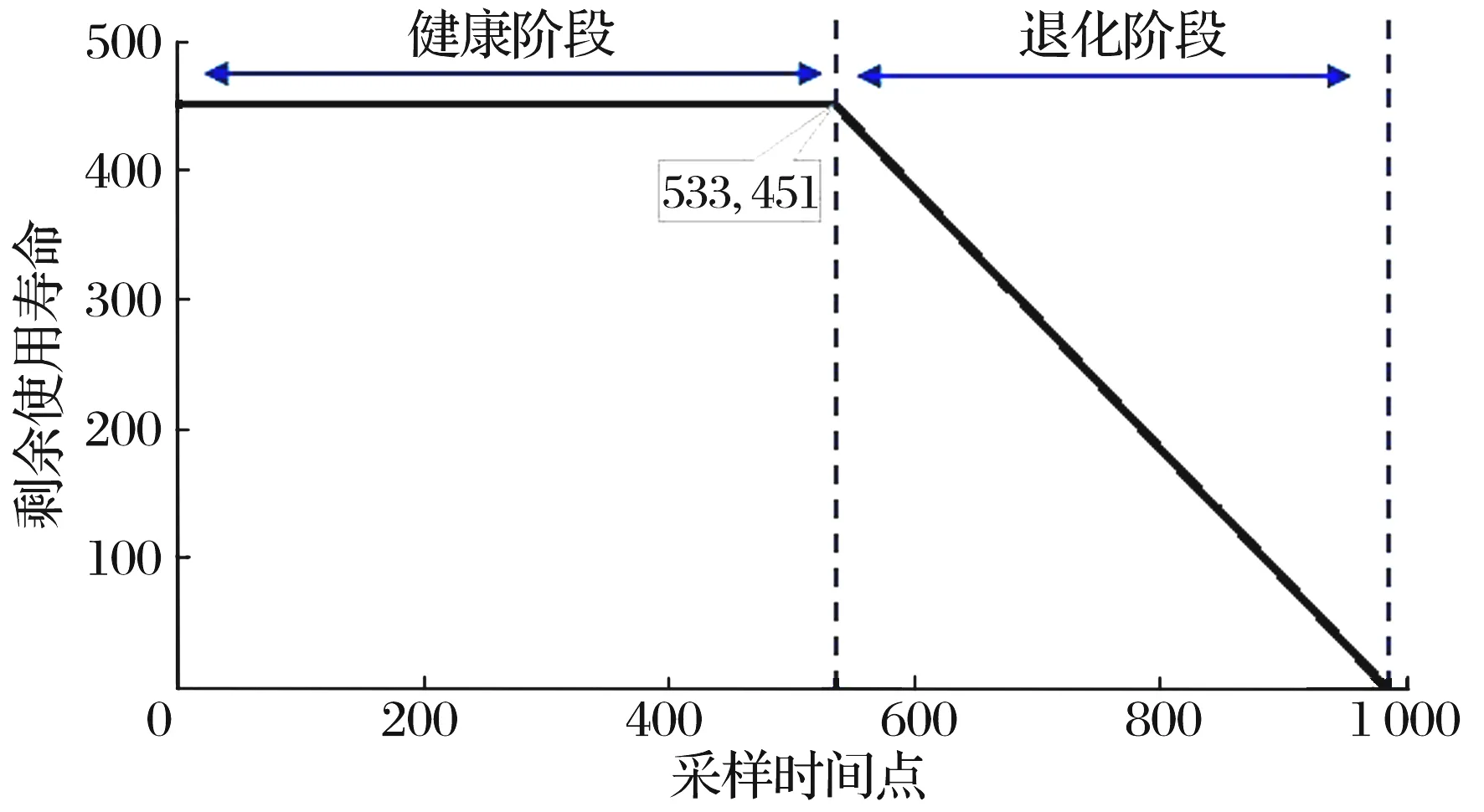
图13 不同初始退化点时的剩余使用寿命分段函数
由图14可知:对于从原始振动信号中提取时频特征再融合降维得到的一维深层特征,其在5 330~7 000 min区间起伏上升明显,故在选取不同初始退化点时,测试集(1 600~2 100 min,即5 330×30%~ 7 000×30%)的预测效果略优于小波去噪和离散小波变换方法,但是第2 100 min之后的预测效果却远不如离散小波变换和变分自编码器相结合的方法,从整体上看,离散小波变换与变分自编码器相结合的方法依旧能达到最优的预测效果。
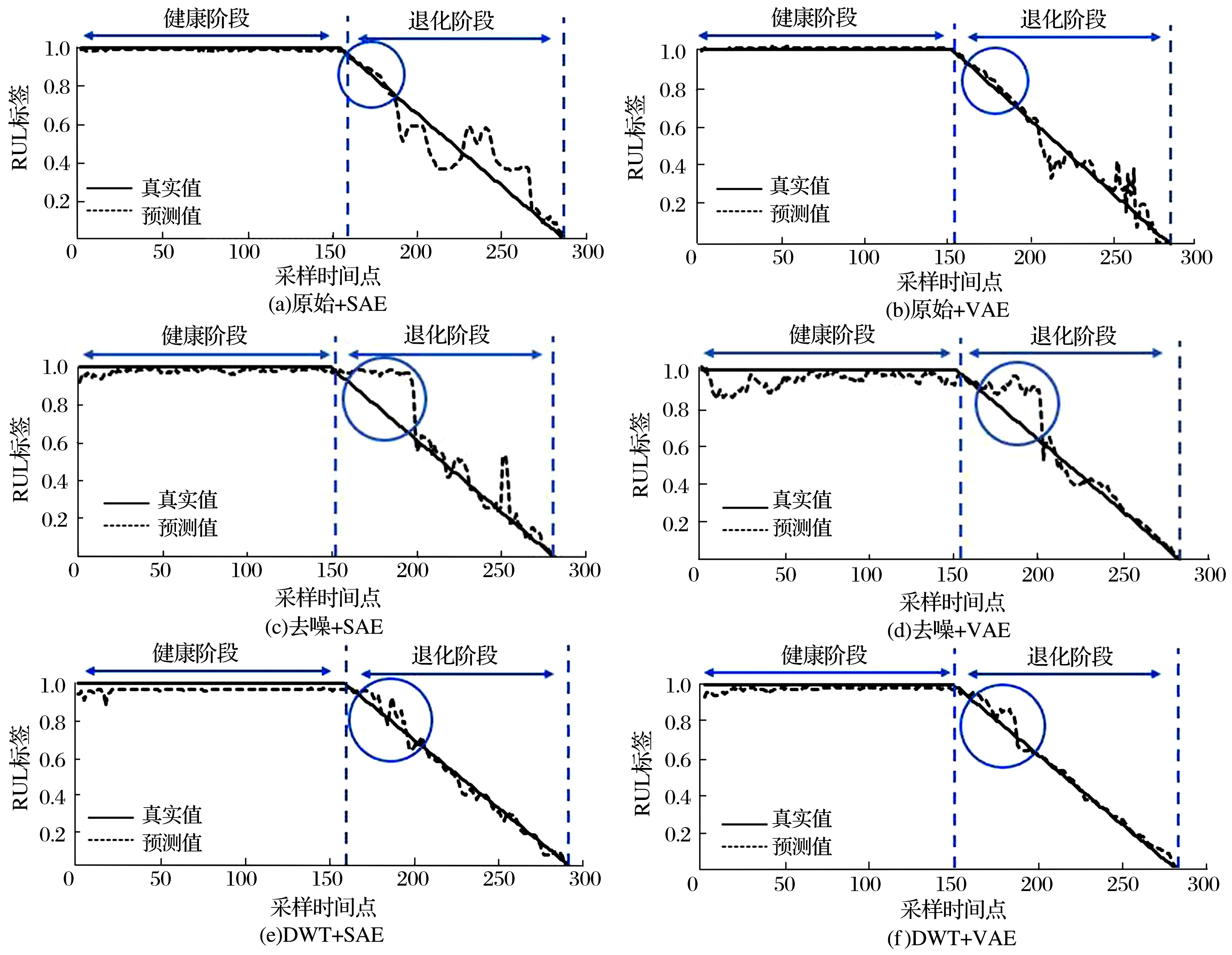
图14 不同初始退化点时各种模型在测试集上的RUL预测结果Fig.14 RUL prediction results of various models on test set at different initial degradation points
3 结束语
针对滚动轴承工作环境中噪声干扰使有效特征难提取的问题,提出一种基于离散小波变换和变分自编码器的轴承剩余使用寿命预测方法,试验结果表明:
1)利用离散小波变换分解信号后对其子分量提取特征,能够有效抑制轴承退化中的“愈合”现象,使提取的特征更具单调趋势性,准确地反映轴承生命周期的退化过程。
2)利用变分自编码器强大的无监督学习能力和抗干扰能力,能够获得综合表征轴承退化趋势的性能指标,从而提高轴承剩余使用寿命预测精度。
3)选择不同初始退化点时,离散小波变换和变分自编码器相结合的特征提取方法依然能精准的预测剩余使用寿命。
