巧用假设法 妙解复杂题
2022-08-15刘振和刘卓安
刘振和 刘卓安
(1.陕西省宝鸡中学 2.宝鸡市长岭中学)
达尔文说过:“最有价值的知识是关于方法的知识.”物理知识含有丰富的方法资源.在物理学习过程中,提炼、积累和运用物理方法,对于深刻理解概念和规律,培养科学思维能力,激发科学探究意识有着不可替代的作用.假设法就是一种常见的重要方法.假设法的应用前提是对概念和规律的深刻理解和具体问题条件的准确把握,据此对物理状态、物理过程、物理趋势或者一些物理量作出一定的假设,然后展开进一步分析推理和探索论证,最终解决问题.假设法为探索复杂问题提供了一种可能的思路,是解决一些疑难问题的有效途径,可以起到常规方法无法替代的作用.
1 假设一种相对运动状态
例1如图1所示,质量为10kg的物体A拴在一个被水平拉伸的弹簧一端,弹簧的拉力为5N 时,物体A处于静止状态.若小车以1m·s-2的加速度向右运动后,则(g取10 m·s-2)( ).
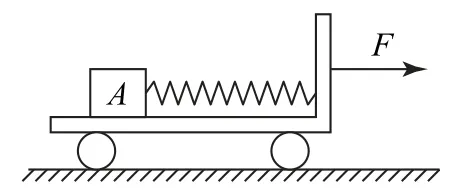
图1
A.物体A相对小车向右运动
B.物体A受到的摩擦力减小
C.物体A受到的摩擦力大小不变
D.物体A受到的弹簧拉力增大

由题意知,弹簧的拉力F弹=5N 时,物体A处于静止状态,则由Ff1=F弹可知物体A受到小车的静摩擦力Ff1大小为5N,方向水平向左,而且可知物体A与小车间的最大静摩擦力Ffm≥5N.若小车以1m·s-2的加速度向右运动,假设物体A随小车一起向右加速而不相对滑动,另假设物体A受到小车对其向右的静摩擦力Ff2,对物体A由牛顿第二定律有Ff2+F弹=ma,则可以算出此时小车对物体A的摩擦力Ff2=5N>0,说明该摩擦力大小为5N,方向向右.由于Ff2=5N≤Fm,没有超过最大静摩擦力,所以A与小车间没有相对运动,此前假设A与小车不相对滑动成立,可以确定弹簧拉力大小、方向不变,故选项A、B、D 错误,选项C正确.本题答案选C.

当几个物体的相对运动情况不确定时,可以假设一个相对运动状态,在此基础上进行分析推理,进而判断假设的正确性,得到物体实际的相对运动状态.本题还有一个假设点,即假设了物体受到的静摩擦力的大小和方向,由牛顿运动定律列方程算出静摩擦力的值,从而得到静摩擦力真实的大小和方向,这也是求解静摩擦力、微小形变弹力等不易直接分析的力的重要方法.
2 假设物体的运动形式
例2如图2所示,一长L=2m、质量M=4kg的薄木板(厚度不计)静止在粗糙的水平台面上,其右端距平台边缘l=5 m,木板的正中央放有一质量为m=1kg的物块(可视为质点),已知木板与平台、物块与木板间的动摩擦因数均为μ1=0.4.现对木板施加一水平向右的恒力F,其大小为48N,g取10m·s-2,求:
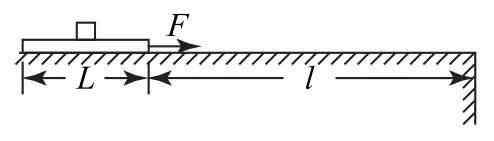
图2
(1)F作用1.2s 时,木板右端与平台边缘的距离;
(2)要使物块最终不能从平台上滑出去,物块与平台间的动摩擦因数μ2应满足的条件.

(1)力F作用后,假设物块与木板会相对滑动,它们均做匀加速运动,但加速度不同.由牛顿第二定律,对木板有

可解得a1=6m·s-2.
对物块有μ1mg=ma2,可解得a2=4m·s-2.
由于a1>a2,故假设成立.
设F作用t时间后,物块恰好从木板左端滑离,则,可解得t=1s.
在此过程中木板对地位移x1==3 m,末速度v1=a1t=6 m·s-1.物块对地位移x2==2m,末速度v2=a2t=4m·s-1.
在物块从木板上滑落后的Δt=(1.2-1)s=0.2s时间内,对木板由牛顿第二定律得F-μ1Mg=,可解得=8m·s-2.
木板发生的位移=v1Δt+=1.36m.此时木板右端距平台边缘Δx=l-x1-=0.64m.
(2)物块滑至平台后,做匀减速直线运动,假设物块与平台间的动摩擦因数为μ20时,物块恰好不能从平台上滑出去,对物块由牛顿第二定律有μ20mg=,解得=μ20g.

要使物块最终不能从平台上滑出去,物块与平台间的动摩擦因数μ2应满足的条件为μ2≥μ20=0.2,即μ2≥0.2.

有时物体运动情况是难以直接判断的,特别是复杂受力下物体运动情况的判断更是一个艰难的过程,而假设物体运动情况可以为我们展开研究推理提供一个方向和途径,使我们得以在此基础上做进一步的分析和计算,从而推断我们假设的科学性,促进问题的解决.
3 假设力所做的功
例3如图3所示,长直轻杆两端分别固定小球A和B,两球质量均为m,两球半径忽略不计,杆的长度为L.先将杆AB竖直靠放在竖直墙上,轻轻拨动小球B,使小球B在水平面上由静止开始向右滑动,当小球A沿墙下滑距离为时,下列说法正确的是(不计一切摩擦,重力加速度为g)( ).
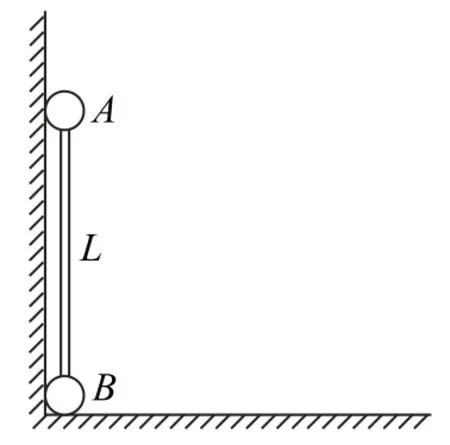
图3




杆对小球的作用力往往是比较复杂的,方向可能沿杆也可能不沿杆,可能对小球做功也可能不做功,做功的正负也不易直接判断,我们用假设法给出一种可能的情况,利用机械能守恒、动能定理等规律进行推理计算,得出功的大小和正负,从而确定杆的弹力是否做功及功的正负.
4 假设一个中介物体
例4如图4所示,内壁光滑、水平放置的玻璃圆环内,有一直径略小于圆环环宽的带正电的小球,以速率v0沿逆时针方向匀速转动(俯视),若在此空间突然加上方向竖直向上、磁感应强度B随时间成正比例增加的变化磁场,且运动过程中小球带电荷量不变,那么( ).
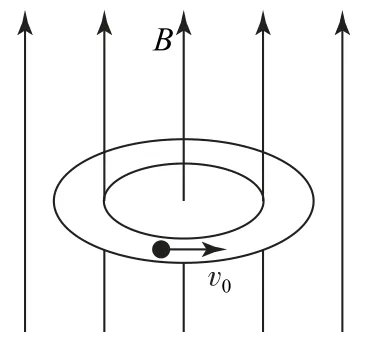
图4
A.小球对玻璃圆环的压力一定不断增大
B.小球所受的磁场力一定不断增大
C.小球先沿逆时针方向减速运动,过一段时间后沿顺时针方向加速运动
D.磁场力对小球一直不做功

本题需要判断感生电场(涡旋电场)方向,可以假设在空间存在一个垂直于磁场的闭合回路,当磁场增强时,闭合回路中的向上的磁通量增加,根据楞次定律,感应电流的磁场方向向下,用安培定则可以判断感应电流的方向从上往下看是顺时针方向,这个方向也就是感生电场的方向.顺时针方向的涡旋电场对小球的电场力先对小球做负功使其速度减为零,后对小球做正功,使其沿顺时针方向做加速运动,故选项C 正确;磁场力始终与小球运动方向垂直,因此始终对小球不做功,故选项D 正确;小球在水平面内沿半径方向受两个力作用:玻璃圆环的弹力FN和磁场的洛伦兹力F,合力充当小球做圆周运动的向心力,其中F=qvB,磁场在增强,小球速度先减小后增大,所以洛伦兹力不一定总在增大,故选项B错误;向心力F向=,其大小随速度先减小后增大,因此挤压力FN不是始终增大,故选项A 错误.本题答案选C、D.

有些物理过程分析起来思维跨度较大,可以假设一个中介物体,借此进行研究,这样可以大大减小思维梯度.对感生电场方向的判断,从方法上讲可以用楞次定律直接判断,但是由于空间往往没有闭合回路,没有感应电流,直接用楞次定律判断感生电场的方向思维跨度较大,不易掌握.所以假设一个闭合回路,可以比较容易地使用楞次定律判断其中的感应电流方向,这个方向也就是感生电场的方向.
5 假设一个变化过程
例5如图5所示,D是一只理想二极管,电流只能从a流向b,而不能从b流向a.平行板电容器的A、B两极板间有一电荷,在P点处于静止状态.以E表示两极板间的电场强度,U表示两极板间的电压,Ep表示电荷在P点的电势能.若保持极板B不动,将极板A稍向上平移,则下列说法正确的是( ).

图5
A.E变小 B.Ep不变
C.U变大 D.电荷将向上加速

保持极板B不动,将极板A稍向上平移时电容器的电容会减小.若假设电容器带电荷量不变,电容器经历一个等电量动态变化过程,由Q=UC可知两板间电压增大,这时的电容器相当于一个电源,其两端电压大于题中电池电动势,所以电路中二极管反接,处于断路状态.说明电容器的放电电路是断开的,电容器电荷量不变的假设是正确的,故选项C正确.由说明电容器电荷量不变的情况下,场强与板间距离无关,不发生变化,故选项A 错误;电荷受到的电场力、重力均不变,电荷仍受力平衡,不运动,选项D 错误.P点的电势φP=UPB=EdPB恒定不变,说明电荷在P点的电势能Ep=qφP保持不变,选项B 正确.本题答案选B、C.
本题也可以先假设电容器两板电压不变,经历一个等电压变化过程.若保持极板B不动,将极板A稍向上平移,电容器的电容减小,由Q=UC可知电容器带电荷量减小,电容器要放电.由于二极管的存在,电容器放电时电流要从右向左通过二极管,二极管是反接的,即电容器放电电路被切断,不会放电,其电荷量保持不变.假设及推理明确电容器电荷量不变后的动态分析与前述分析过程一样,可使问题得以解答.

本题由于存在二极管,电容器的动态变化到底是保持电荷量不变还是保持电压不变,需要作分析判断,可以假设其经历一个电荷量不变或电压不变的过程,利用平行板电容器电容变化规律、二极管特点和电路规律,综合分析判断,确定实际到底是怎样的过程.
6 假设最终稳定状态
例6如图6所示,蹄形磁铁和矩形线圈均可绕竖直轴OO′转动.从上向下看,当蹄形磁铁在外力作用下逆时针匀速转动时,则( ).

图6
A.线圈将逆时针转动,转速与磁铁相同
B.线圈将逆时针转动,转速比磁铁小
C.线圈转动时将产生感应电流
D.线圈转动时感应电流的方向始终是abcda

当蹄形磁铁在外力作用下逆时针匀速转动时,线圈中由于存在电磁感应产生感应电流,感应电流的安培力作用是阻碍相对运动,所以线圈也随之逆时针转动.达到稳定状态后,假设线圈转速与磁铁相同,则线圈中磁通量就不再变化,线圈中就没有感应电流,就没有安培力充当动力克服线圈所受阻力,从而支持它持续运动,该假设错误;假设线圈比磁铁转动得快,则违背了能量守恒定律;假设线圈达到稳定状态时逆时针转动,转速比磁铁转速小,则线圈与磁铁之间始终有相对运动,线圈中磁通量会发生变化(有的时段增大,有的时段减小),有感应电流,方向有时为abcda,有时为adcba,但所受安培力总是阻碍相对运动,提供动力使线圈持续运动,所以该假设是正确的.故选项A、D 错误.答案为B、C.

许多复杂运动的最终稳定状态用一般方法分析是困难的,假设法可以跳出常规思维模式,摆脱常规的分析思路束缚,假设出一些结论,然后依据相关物理规律进行必要的分析推理,从而可以快速、简捷地确定运动的最终稳定状态.
同学们,深入挖掘物理知识中的方法资源,巧妙使用假设法等物理方法,可以使物理学习更高效,使物理问题的解决更灵活、更快捷.
链接练习
1.如图7所示,倾角为θ的斜面上放置一滑块M,在滑块M上放置一个质量为m的物块,滑块M和物块m相对静止,一起沿斜面匀速下滑,下列说法正确的是( ).
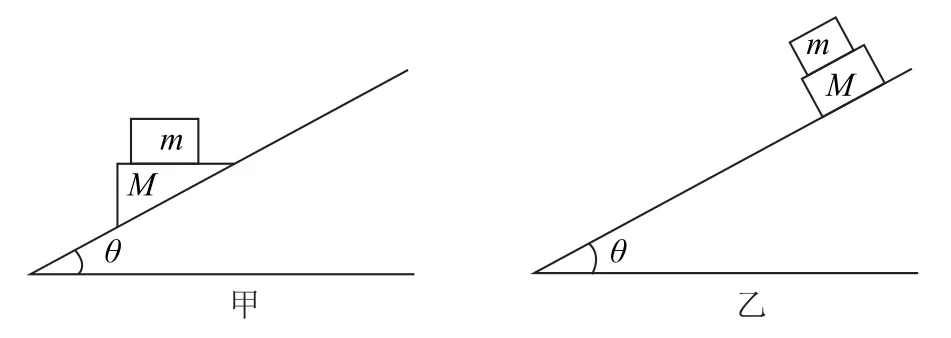
图7
A.图甲中物块m受到摩擦力
B.图乙中物块m受到摩擦力
C.图甲中物块m受到水平向左的摩擦力
D.图乙中物块m受到与斜面平行向上的摩擦力
2.如图8所示,A、B两物体叠放在水平地面上,A物体质量m=20 kg,B物体质量M=30kg.处于水平位置的轻弹簧一端固定于墙壁,另一端与A物体相连,轻弹簧处于自然状态,其劲度系数为250N·m-1,A与B之间、B与地面之间的动摩擦因数均为μ=0.5.现用一水平推力F作用于物体B上使B缓慢地向墙壁移动,当移动0.2m 时,水平推力F的大小为(已知A、B之间的最大静摩擦力等于滑动摩擦力,g取10m·s-2)( ).
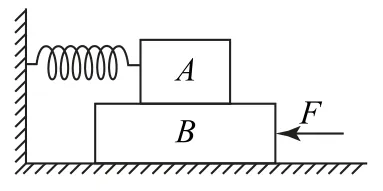
图8
A.350N B.300N C.250N D.200N
3.如 图9 所 示,甲、乙两车在比赛车道上比赛,某一时刻,乙车在甲车前方L1=11 m处,乙车速度v乙=60 m·s-1,甲车速度v甲=50 m·s-1,此时乙车离终点线尚有L2=600m.若甲车加速运动,加速度a=2m·s-2,乙车速度不变,不计车长.则

图9
(1)经过多长时间甲、乙两赛车间距离最大,最大距离是多少?
(2)到达终点时甲车能否追上乙车?
链接练习参考答案
1.B、D.2.B.3.(1)5s,36m;(2)不能.
(完)
