物体走最短距离所用时间是否最短?

张 睿 常玉如

(1.山东省青岛第二中学 2.北京市育英学校)

两点之间线段最短.物体由静止释放,走最短的距离所用的时间是否最短? 本文对物体沿光滑斜面下滑和沿光滑曲面自由下滑两种情况所用时间进行对比,得出物体走最短距离所用时间并非最短.进一步研究物体自由释放沿哪种路径所用时间最短,从而得出最速曲线方程.

【题例】如图1 所示,将完全相同的两个小球1、2分别从同一高度由静止释放,其中甲是一倾角为45°的光滑固定斜面,乙为光滑固定圆弧,不计空气阻力,则二者落地的时间大小关系如何?

图1

解法1 微元法

图2

因此t2＜t1.

解法2图像法

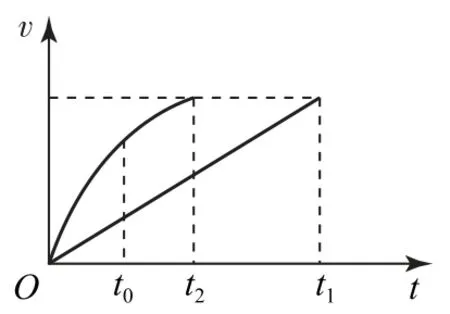
图3

【问题思考】物体走最短距离所用时间并不是最短,物体沿什么样的路径下滑时间才会最短呢?

分析设O、A是高度不同,且不在同一铅垂线上的两定点,如果不计摩擦和空气阻力,一质点m在重力作用下从O点沿一曲线降落至A(p,q)点,如图4所示.

设曲线为y＝y(x),坐标如图4所示,质点由O点开始运动,它的速度v与它的纵坐标关系为v＝,其中g为重力加速度.

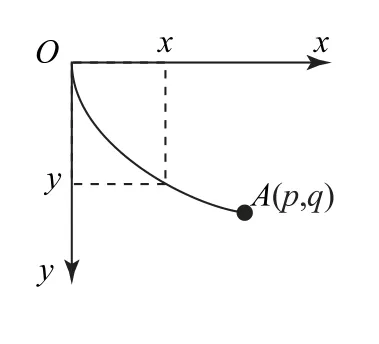
图4

在曲线上点(x,y)处,质点的运动速度

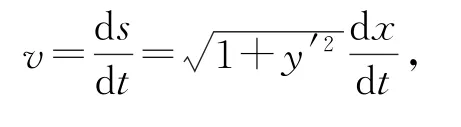
式中,s表示曲线的弧长,t表示时间,于是有

由于O、A两点的横坐标分别是0、p,则质点m从O点运动到A点所需时间

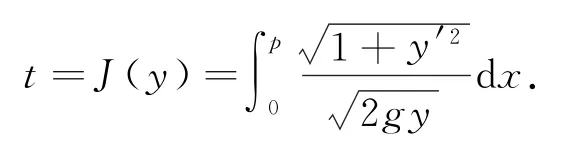
这样质点由O点运动到A点所需时间t是y(x)的函数,最速降线问题就是满足边界条件的y(0)＝0,y(p)＝q所有连续函数y(x)中,求出一个函数y使泛函数取最小值.

对泛函数求极值的问题称为变分问题,使泛函取极值的函数称为变分问题的解,也称为极值函数.若

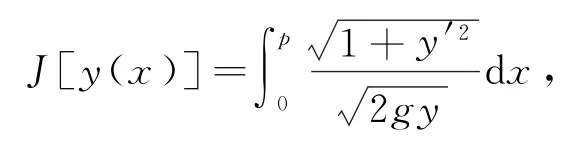
且y(0)＝0,y(p)＝q.这样取

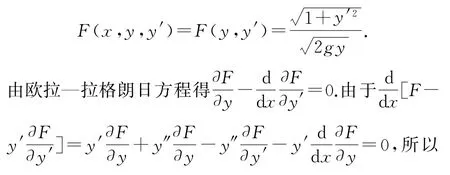
上式对θ求导,所以x＝r(θ－cosθ)＋x0.根据曲线过原点(0,0)及(p,q),可求出x0＝0及r,这样,所求曲线为x＝r(θ－sinθ),y＝r(1－cosθ).

可以看出,最快下降路线是一条滚轮线或者说是一条摆线.摆线就是当一个圆环沿着一条直线向前无滑滚动时,圆周上某一点P所形成的运动轨迹.

(完)