化学反应方程式配平的方法归类

但世辉 齐 婷

(1.湖北省襄阳市东风中学 2.湖北省襄阳市第四中学)

1 化学方程式配平的常用方法

1.1 常用的方法——最小公倍数法

最小公倍数法的核心是利用三大守恒中的“得失电子守恒”这一原则,找出反应前后变价元素化合价的变化值,求出得失电子个数,通过最小公倍数法,保证反应前后化合价的升降总数相等,进而先求出氧化剂、还原剂、氧化产物、还原产物的化学计量数,再用元素守恒、电荷守恒等原则配平其他物质的化学计量数.

例1配平离子反应方程式:ClO－＋Fe(OH)3＋OH－→Cl－＋＋H2O.

分析根据化合价的变化值找出ClO－和Fe(OH)3转移的电子数分别为2和3,二者的最小公倍数为6,为保证电子转移总数相等,故ClO－和Fe(OH)3的化学计量数分别为3和2,再根据元素守恒和电荷守恒配平余下物质的化学计量数,最终求出结果:3ClO－＋2Fe(OH)3＋4OH－＝3Cl－＋＋5H2O.

例1配平的过程是习惯性地从左向右进行配平,即正向配平,实际上,对于一些特殊的氧化还原反应(部分分解反应、歧化反应等),采用逆向配平的思维反而会简化解题过程.

例2配平化学方程式:P4＋KOH＋H2O→K3PO4＋PH3.

分析仍然使用最小公倍数法进行配平,倘若采用正向配平,由于变价元素为P,化合价升高和降低的数目均集中在P4中,无法分开,难以单独找出得失电子个数,最小公倍数和化学计量数的判断也无从下手.此种情况应该采用逆向配平法:K3PO4和PH3转移的电子数分别为5和3,最小公倍数为15,化学计量数分别为3和5,根据元素守恒进而完成其他物质的配平:2P4＋9KOH＋3H2O＝3K3PO4＋5PH3.

1.2 实用的技巧——分数法

对于有单质出现的化学反应方程式,其大多属于氧化还原反应,若用最小公倍数法配平肯定没问题,但需要分析得失电子个数,若使用分数法进行配平,则过程会得以简化,具体方法为:以三大原则中的“元素守恒”为依据,利用观察法,先找出单质之外的其他物质的化学计量数,再以单质中相应元素的守恒为依据,确定单质的化学计量数(很可能是分数).由于单质只有一种元素,其化学计量数即使是分数也不会影响其他元素的守恒,这便是分数配平法的核心.以例2为例进行说明:先配平K 元素可推知K3PO4和KOH的化学计量数分别为1和3,再根据O 元素守恒,可推知H2O 的化学计量数为1,根据H 元素守恒,可推知PH3的化学计量数为5/3,最后根据P 元素守恒,可推知P4的化学计量数为2/3,左右同时扩大3倍,得出正解.

很明显,分数配平过程只用到了元素守恒,并未使用得失电子守恒,绕开了使用最小公倍数法必须找出电子转移数这一麻烦,配平过程直接明了.对于一些有单质出现的化学方程式,使用分数法配平更为简单,尤其是对于一些元素化合价难以确定并且有单质出现的化学方程式更为适用.

例3配平化学方程式:FeS2＋O2→SO2＋Fe2O3.

分析对于初学者而言,FeS2中各元素化合价难以确定,使用最小公倍数法配平则稍显吃力,但是因为O2为单质,所以可用分数法完成配平:先根据铁元素守恒,可推知Fe2O3、FeS2的化学计量数分别为1和2,然后根据S元素守恒,可推知SO2的化学计量数为4,再根据O 元素守恒,可推知O2的化学计量数为,最后左右同时扩大2倍可得正解:

1.3 虚拟的方法——零价法和设1法

对于一些元素化合价难以确定的物质,比如含较多变价元素的物质、原子个数带字母的物质等,使用最小公倍数法计算得失电子个数,显然很难完成,此时可借助零价法进行配平:将难以确定化合价的化合物中所有元素的化合价均假设为零,这样既可以保证找到该元素的化合价,又能回避复杂化合物元素化合价难以确定的问题,便于后面计算得失电子个数,同时也保证了整个化合物的化合价总和为零,这就是零价配平法的原则.很显然,化合价为零是虚拟出来的,只是为了简化问题,后续依旧要依据得失电子守恒进行配平.

例4配平方程式:Fe3C＋HNO3→Fe(NO3)3＋NO↑＋CO2↑＋H2O.

分析由于Fe和C均为多价态元素,导致Fe3C中Fe和C的化合价存在多种可能,难以确定,无法进一步使用最小公倍数法进行配平.此时使用零价配平法:虚拟Fe3C 中元素Fe和C 的化合价均为0,根据Fe元素守恒,Fe(NO3)3的化学计量数暂定为3,整个反应过程,失电子总数为Fe(9个)和C(4个)的总和13,得电子总数为N 的(3个),二者的最小公倍数为39,根据逆向配平法推知NO 的化学计量数为13,CO2的化学计量数为3,Fe(NO3)3的化学计量数扩大3倍,即为9,根据Fe元素守恒推知Fe3C的化学计量数为3,根据N 元素和H 元素守恒,推知HNO3和H2O 的化学计量数分别为40、20,最终得出正解:

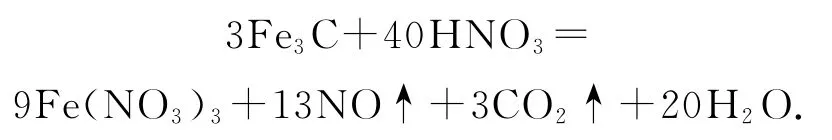
与零价配平法虚拟出零价价态类似,对于一些组成较为复杂的化合物,配平时可虚拟出该物质的化学计量数为1,这样可把复杂物质的化学计量数最简化,后续使用元素守恒确定其他物质化学计量数的时候便更容易进行,避开了复杂的得失电子数计算这一环节.

第1步,化合价升降相等,则有

第2步,电荷守恒,求得OH－系数为6m－6.

第3步,H 元素守恒,求得H2O 系数为3m－3.

2 两类复杂方程式的配平

2.1 具有多解情况的化学方程式的配平

有一种类型的化学反应方程式,其特点是:反应过程中化合价变化的情况存在3种或者3种以上,称之为多解化学方程式,其物质的化学计量数存在多种可能,至于为什么化学计量数存在多解,以下例进行说明.

例6配平化学反应方程式:HClO3→HClO4＋Cl2＋O2＋H2O.

分析该方程式中变化情况有3种:Cl(＋5价升为＋7价)、Cl(＋5价降为0价)、O(－2价升为0价).为便于计算得失电子数,采用逆向配平法,设HClO4、Cl2、O2的化学计量数分别为x、y、z,根据得失电子守恒可列方程:

化简得:x＝5y－2z,该方程为三元一次方程,存在多解,因此,该化学反应方程式在配平上也会存在多种化学计量数(如表1).

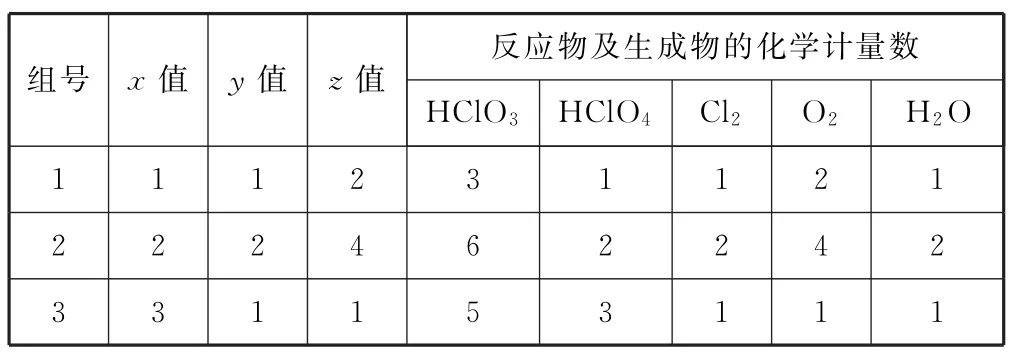
表1 例6各物质化学计量数的多解可能(部分)

从上题中可以看出,对于多解化学方程式的配平,主要还是依据三大守恒中的得失电子守恒和元素守恒(若为离子反应方程式,自然要满足电荷守恒)来进行配平,其多解的根本原因在于:变价情况存在多解,在进行得失电子守恒计算时便会推导出满足该守恒的多种可能,上题中列出的三元一次方程式就是最好的体现.

对于变价情况达到4种或者4种以上,在具体配平的过程中,为了减少未知数的个数便于求解,往往需要用到设1法,再结合三大守恒列方程进行推导.

例7配平离子反应方程式:

表2 例7各物质化学计量数的多解可能(部分)

综合以上两道例题可以看出:对于多解的化学方程式,虽然配平的可能性理论上存在多种情况,但在三大守恒的基础上巧妙使用设1 法、最小公倍数法等,求出部分配平的结果并非难事,问题在于,对于这些多解到底该如何取舍呢? 一是要看题目的具体要求.配平出来的结果从理论上来说都能存在,不能说没有意义,更不能说这些反应没有发生,此时可根据题目要求,假如题目中给定了实验时所用反应物的物质的量之比,则必须按照试题要求选取正解,比如若例7题目中规定化学计量数尽可能取最小正整数,则正解应该为第3组情况.二是根据统计热力学原理进行取舍.根据统计热力学原理,化学反应实际上是杂乱分子有效碰撞的结果,多个微观粒子发生碰撞的概率小,而少个粒子发生有效碰撞的概率要大得多,化学方程式的配平结果中反应物计量数总数最小时最接近客观事实.根据该理论,例6应该采用组号1,例7应该采用组号3完成配平.

2.2 有机物局部基团原子化合价发生变化的化学方程式的配平

所谓有机物局部基团原子化合价发生变化的方程式,是指有机物中部分基团被氧化或者被还原成新的基团,该基团中某些原子化合价发生变化,但除了这些基团之外,有机物其他构成部分并未参与氧化还原反应的过程.此类反应是相对于有机物彻底被氧化或者被还原的反应方程式而言,以例8和例9为例进行对比说明.

例8配平反应方程式:CH3CH2OH＋O2→CO2＋H2O.

例9配平反应方程式:C6H5—CH3＋KMnO4＋H2SO4→C6H5—COOH＋MnSO4＋K2SO4＋H2O.

分析对于例8,有机物CH3CH2OH 中的所有碳原子均参与了氧化还原反应过程,均被氧化成了CO2,化合价由－2 升高至＋4(CH3CH2OH 中的化合价由氢、氧2种元素的化合价进行推导,其中将氢、氧2种元素的化合价看成是＋1、－2,求出碳的平均化合价为－2).配平该类有机化学反应方程式较为简单,可用分数法最后配平O2的化学计量数,也可用最小公倍数法直接配平,不再赘述.

相对于例8,例9明显不同:有机物C6H5—CH3并不是所有碳原子均参与了氧化还原过程,只有基团—CH3被氧化成了—COOH,而C6H5—反应前后并没有变化.倘若使用最小公倍数法,利用得失电子守恒进行配平,则需要求出整个有机物中7个碳的平均化合价,一是非常麻烦,二是不符合反应事实(因为将氧化了的和未被氧化的碳原子全部看作参与了氧化还原过程).为避开这些问题,简化配平过程,可以只关注被氧化基团中原子化合价的变化情况,借用零价法的原理,将被氧化的基团和氧化生成的相应基团的总化合价确定为0,氢、氧原子的化合价看作＋1、－2,分析被氧化基团内的原子在反应前后化合价的变化情况,再根据得失电子守恒利用最小公倍数法进行配平.

对于例9,首先明确只有—CH3被氧化成了—COOH,其他基团没有参与氧化还原过程,设定—CH3和—COOH 的总化合价为0,根据碳、氢的化合价可推出—CH3中的碳的化合价为－3,—COOH中碳的化合价为＋3,该过程转移电子数为6,另外一边KMnO4转化为MnSO4,电子转移数为5,根据最小公倍数法可快速找出C6H5—COOH 和MnSO4的化学计量数分别为5、6,再根据元素守恒可配平其他物质的化学计量数得到正解:

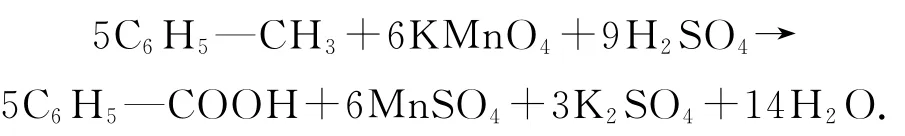
对于只有部分基团原子化合价发生变化的有机反应,配平时只关注变价原子所在的基团,将该基团视作反应物,关键点在于找准该反应物参与氧化还原反应过程之后的生成物,然后对照分析该反应物和生成物,在得失电子守恒的基础上利用最小公倍数法进行配平.

化学方程式配平的方法和技巧很多,不管如何配平,一定要遵循三大守恒:元素守恒、电荷守恒和得失电子守恒,在具体配平的过程中,目的是快速高效地完成配平,这就需要根据所配方程式本身的特点去选用最合适的配平方法从而灵活处理(如表3).

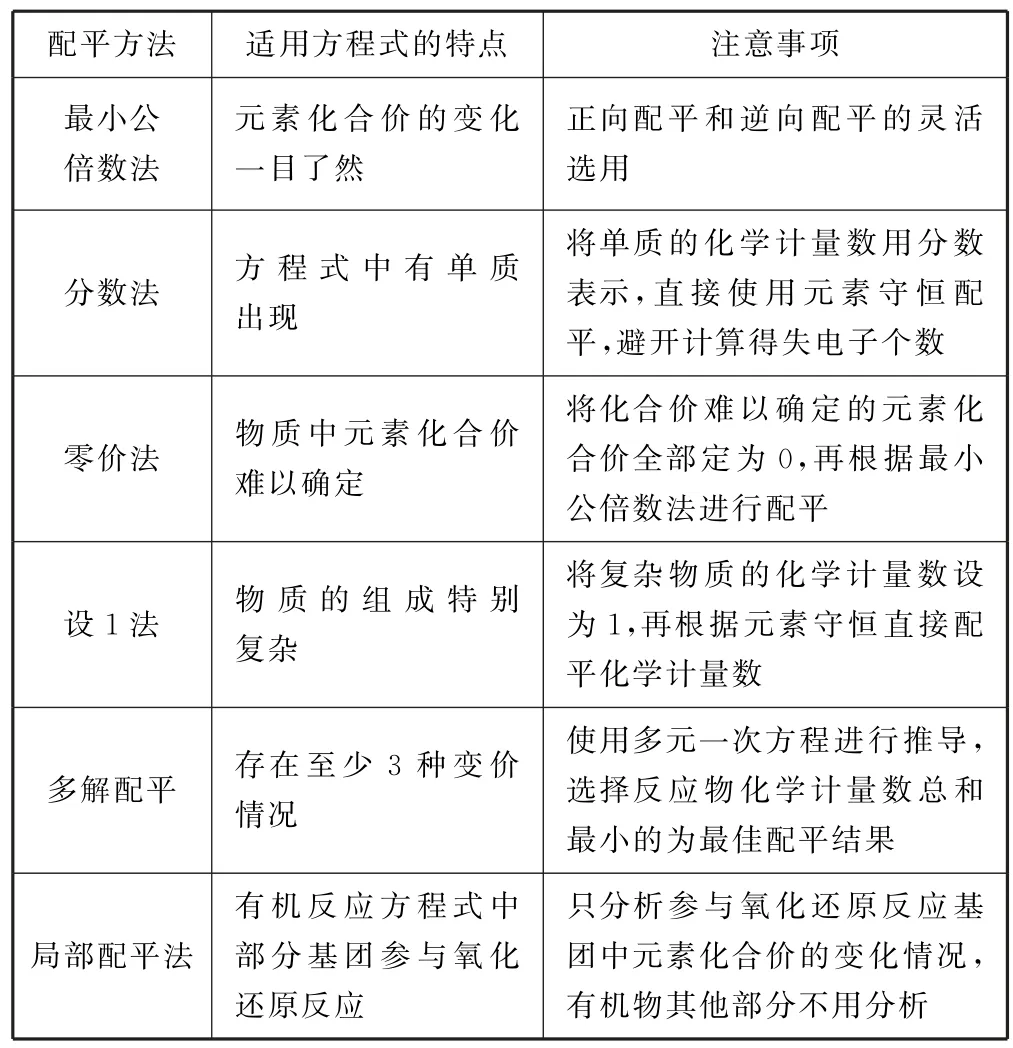
表3 化学方程式配平的方法总结

(完)