对流扩散方程的保正守恒特征有限体积法研究❋
2022-08-15李昕姝
李昕姝, 付 凯
(中国海洋大学数学科学学院, 山东 青岛 266100)
对流扩散方程广泛应用于众多科学技术领域,如大气环境计算,油藏开发数值模拟,地下水污染防控和金融计算等领域[1-5]。由于该方程通常不存在精确解,因此开发其数值求解方法进行计算模拟具有十分重要的实际应用价值。
对流占优扩散方程的数值求解是一项极具挑战性的工作。在网格尺寸和时间步长不够充分小时,传统的有限差分、有限体积或有限元方法通常不能得到较好的结果,在陡峭前沿会出现虚假的非物理振荡或过度的数值耗散。
为了克服求解对流占优扩散问题的困难,学者们提出了许多基于特征线方法的数值格式。从物理角度,特征线方法可以有效地求解沿流线问题,得到更为精确的近似结果;从计算角度,特征线方法可以使用较大的时间步长,因此可大幅降低计算成本[6]。Douglas和Russell提出了用于解决一维对流占优扩散问题的特征线修正方法[7]。随后,Bermejo,Dawson和Hansbo等进一步发展了时间一阶特征线方法用于解决高维对流扩散问题[8-12],Fu,Liang和Rui等提出了时间二阶数值格式[6,13-15]。
科学家和工程师们通常希望数值解能够准确地反映现实问题的物理性质,如保正性和守恒性等[15,16-21]。众所周知,特征线方法需要在对前一时间层上追踪点或追踪单元处的解进行近似。Colella和 Woodward关于对流方程的求解提出了一种分段抛物方法(PPM),该方法满足局部质量守恒[22]。将特征线法与守恒插值结合,Fu和Liang提出了求解对流扩散问题的高阶守恒方法[6,13,15],但未对保正性进行研究。对于解的保正性和守恒性,通过引入限制器进行修正是一种有效的实现方法。Liu,Zhang和Zhu等提出的局部限制器可以在保持格式二阶精度的基础上满足保正性和质量守恒[23-24]。
本文提出了对流占优扩散方程保正守恒特征有限体积法。通过将特征线方法和有限体积法相结合,对前一时间层追踪单元上的解采用带保正约束的二阶精度守恒分段抛物插值近似,并运用沿特征线取平均和局部限制器,得到时间二阶保正守恒特征有限体积方法。我们给出了保正性和质量守恒性的理论证明。对旋转速度场中的Gaussian hill的输运问题和陡峭前沿移动问题进行了数值实验,验证了方法在时间和空间上的精度和保正性。通过计算离散质量误差,证明了格式具有质量守恒。
1 数值格式
1.1 保正守恒特征有限体积法
考虑如下二维对流扩散方程
(x,y,t)∈Ω×(0,T];
α▽u(x,y,t)·nΩ=0, (x,y,t)∈∂Ω×(0,T];
u(x,y,0)=u0(x,y), (x,y)∈Ω。
(1)
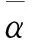
对二维区域Ω=[ax,bx]×[ay,by],给出如下剖分
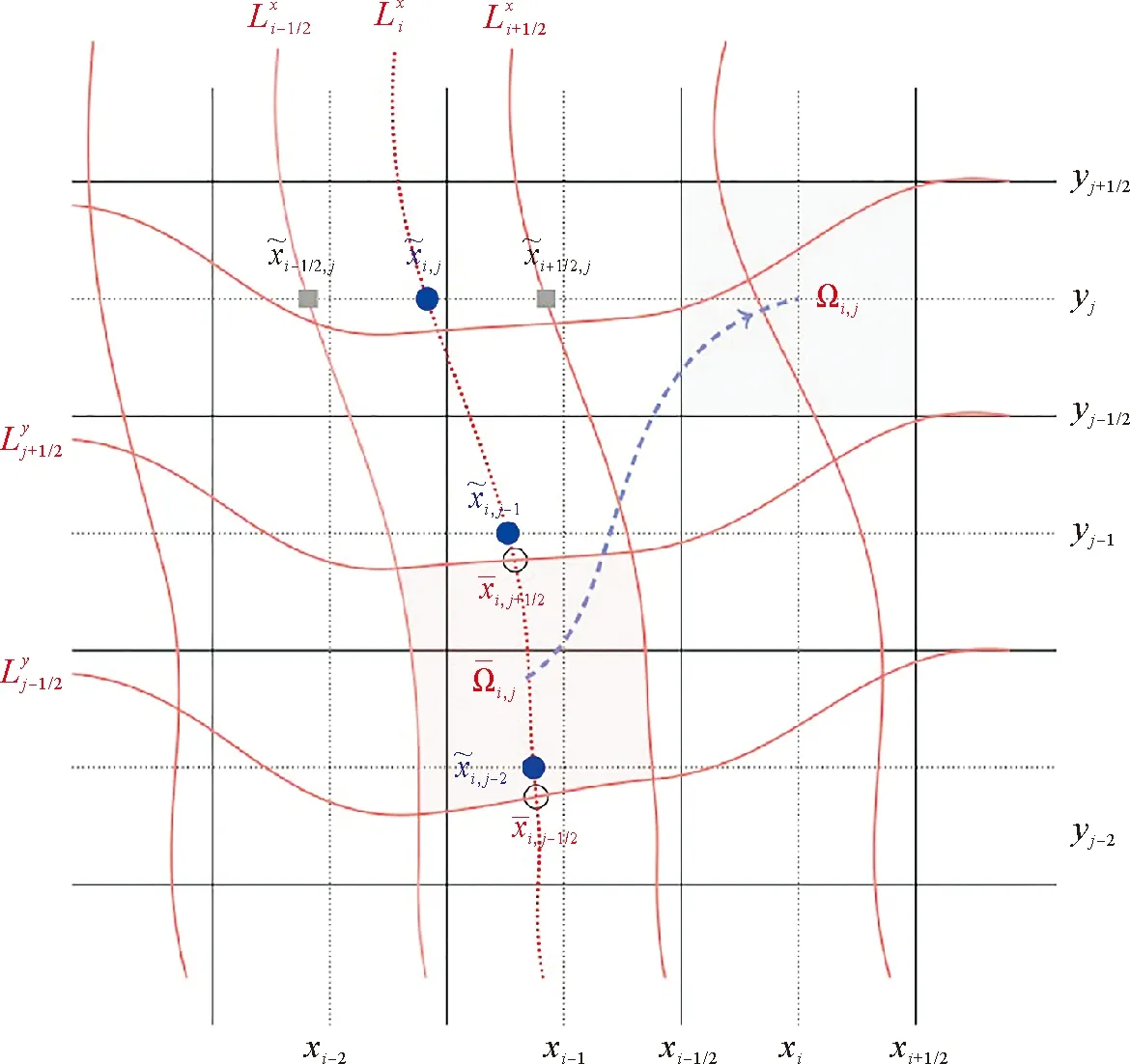
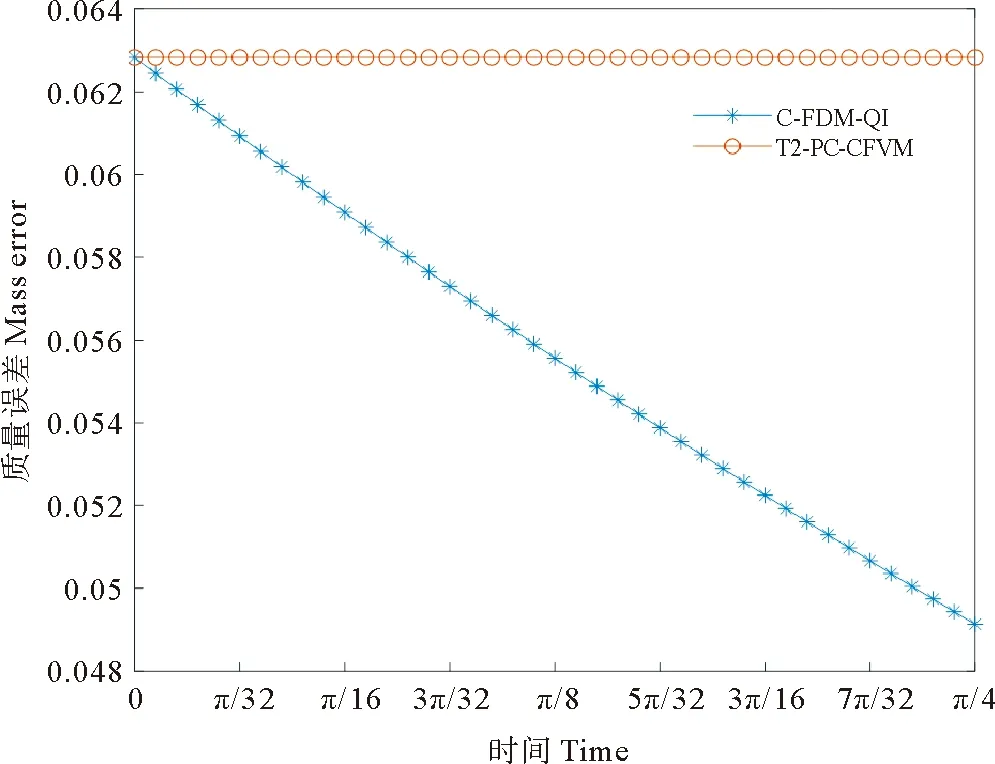
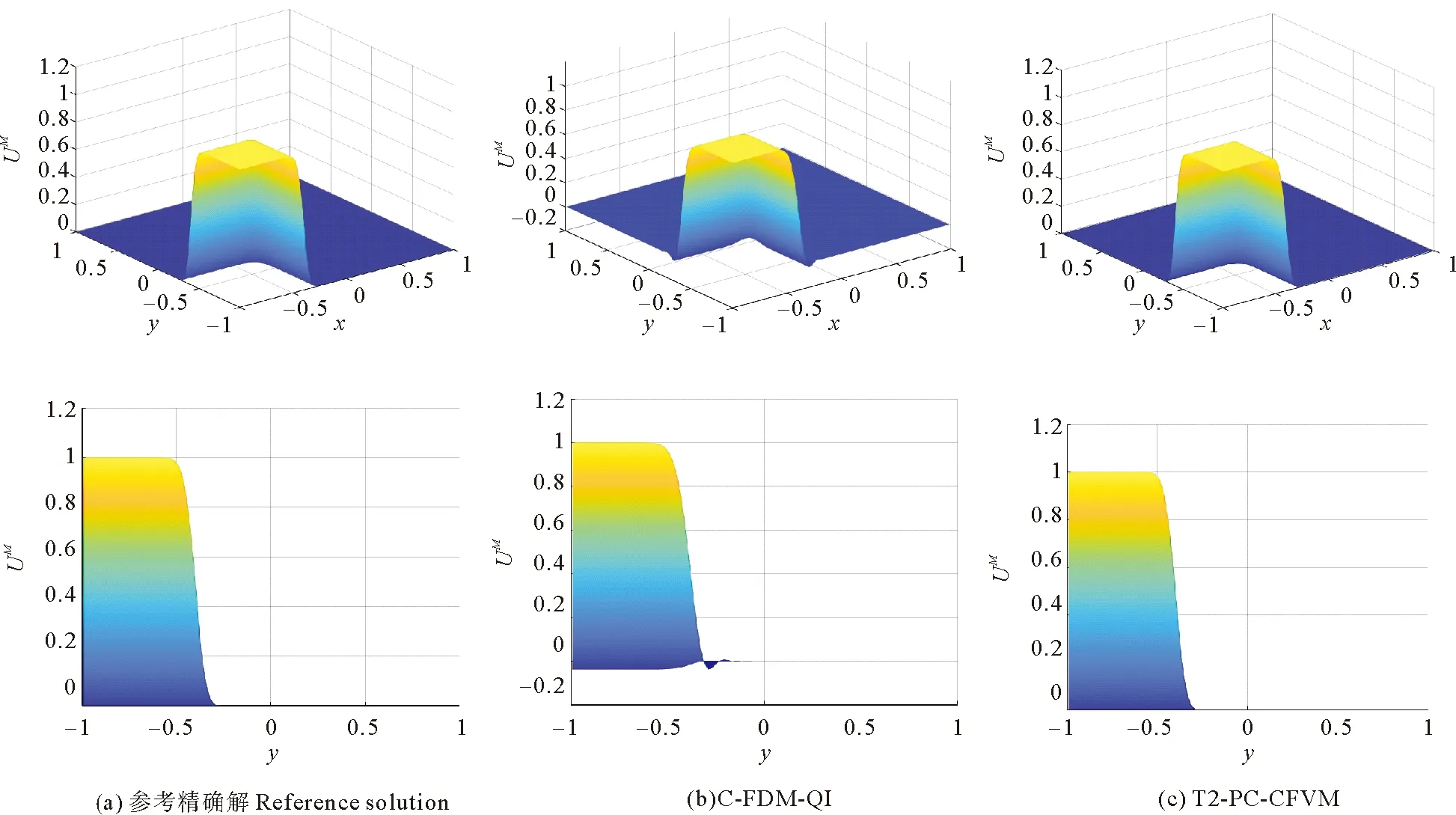
ax=x1/2 (2) 对于i=1,2,…,Nx,j=1,2,…,Ny,定义欧拉单元,单元中心和单元大小为 Ωi,j=[xi-1/2,xi+1/2]×[yj-1/2,yj+1/2], (3) (4) (5) 令 (6) 对于时间离散,取均匀剖分。令Δt=T/M,tm=mΔt,m=0,1,2,…,M。 应用特征线法[7],令 ψ(x,y)=[1+β1(x,y)2+β2(x,y)2]1/2, (7) 用τ表示与算子∂tu+β1∂xu+β2∂yu相关联的特征方向, (8) 过tm时刻x=(x,y)点的特征线满足常微分方程 (9) (10) 每个Ωi,j在t时刻对应的特征单元记为 t∈[tm-1,tm]}, (11) 在tm-1时刻的特征单元记为 (12) 定义时空单元 (13) (14) 通过沿特征线取平均来处理扩散项,给出如下时间二阶近似: (15) (16) (17) 对于在tm时刻的扩散项,定义 v1(x,y,t)=-α1(x,y)ux(x,y,t), (18) 则 (19) 其中 (20) (21) 由于追踪单元的边界通常不与欧拉网格线平行,因此对tm-1时刻的扩散项进行高精度计算较为困难。为得到高精度质量守恒数值解,应用分片抛物函数在Ωi,j上近似Um-1来计算追踪单元边界扩散通量[6]。该方案可保证tm-1时刻扩散通量的计算精度及其在追踪单元边界的连续性。将其近似为 (22) 综上可得二维对流占优扩散问题(1)的时间二阶格式 (23) 令 (24) (25) 初始条件 (26) 边界条件 (27) (细黑线代表欧拉线,红色线代表拉格朗日线,虚线代表中线。红色单元是与灰色欧拉单元Ωi,j相对应的拉格朗日追踪单元 associated with gray Eulerian cell Ωi,j.) 第一步沿y=yj,j=1,…,Ny进行计算。定义守恒插值 [Hm-1]p,j,p=1,…,Nx, [Hm-1]p,j(x)= (28) 满足如下条件 (29) (30) (31) [Hm-1]p,j表示在区间[xp-1/2,xp+1/2]上沿欧拉线y=yj方向的守恒插值分布。 U0,j=U1,j, (32) (33) (34) 满足如下条件 (35) (36) 为使得所构造出的 PPM 插值函数(见公式(28))满足保正性,引入如下约束: IfUmin<0,then else If else end end end 假设1速度β满足如下条件 (37) (38) 证明 对式(24)从i=1到Nx和j=1到Ny求和 由于在tm-1时刻扩散通量在追踪单元边界的连续性,对于相邻的两个拉格朗日单元,通过一个边界流入单元的量等于其他单元通过该边界流出的量[6],并注意边界条件(公式(27))可得 即得证。 (39) 定义如下限制器: (40) 其中 (41) 定理1限制器(40)具有如下性质: (42) 则 证明 ① 将式(41)代入式(40),并注意M的定义,可直接得出保正性。 ② 由式(42),可得 (43) 其矩阵形式为 AmUm=U*, (44) 其中 引理2[27-28]对于一个不可约矩阵A=(aij)N×N满足aii>0(1≤i≤N)和aij≤0(1≤i,j≤N,i≠j),如果A为行弱对角占优,即 (45) 且至少有一个不等式是严格大于零,则矩阵A是一个M矩阵,A-1中的所有元素均为非负的。 定理2在假设1和Neumann边界条件下,格式 T2-PC-BFVM(见公式(25))具有如下性质: (46) ② 质量守恒: (47) 则 注意边界条件(27),可得 因此 质量守恒性得证。 在本节中,通过数值算例验证了二维对流扩散问题时间二阶保正守恒特征有限体积法(T2-PC-CFVM)的精度和性质。定义tm时刻数值解的离散质量误差 (48) 用于评估数值格式的守恒性。 算例1首先考虑区域Ω=[-1.5,1.5]×[-1.5,1.5]上的Gaussian hill 旋转问题。速度场β=(4y,-4x)T;扩散系数α1=α2=1×10-3。问题的精确解为 (49) 其中 (x0,y0)=(-0.5,0),σ=0.1。 (50) 初始条件由式(49)中t=0给出。 数值试验中将新格式与Douglas和Russell[7]提出的双二次插值标准特征有限差分(Characteristic finite difference method with biquadratic interpolation,C-FDM-QI)进行了比较,计算了两种方法的收敛阶。取T=π/4,扩散系数α1=α2=1×10-3和均匀网格。选择空间步长h=2.5×10-3,以使得空间误差足够小,选择时间网格点数M=20、24、28、32和36用于计算时间收敛阶。表1列出了不同数值格式误差的L2范数(E2)和时间阶。从表1的结果中可以很明显的看出,T2-PC-CFVM格式具有时间二阶精度,而C-FDM-QI为一阶精度。选择时间网格数M=2 000和空间步长h=1/50、1/60、1/70、1/80 和1/90,对空间阶进行了计算。如表2所示,两种格式均为二阶精度。 表1 格式C-FDM-QI和T2-PC-CFVM所得解的误差、时间收敛阶、最小值和质量误差 表2 格式C-FDM-QI和T2-PC-CFVM所得解的误差、空间收敛阶、最小值和质量误差 关于保正性,由表2列出不同结果的最小值可以看出T2-PC-CFVM得到非负结果,而C-FDM-QI会产生负值,例如,当空间步长为h=1/50的时,C-FDM-QI格式的最小值为-1.170 4×10-3,T2-PC-CFVM格式的最小值为0。图2给出了在T=π/4时刻,应用空间网格N=100和时间网格数M=100得到的精确解,以及C-FDM-QI和T2-PC-CFVM数值解的侧视图。可以看出格式T2-PC-CFVM的结果均为非负值,而格式C-FDM-QI产生了明显的负值。 图2 精确解和不同格式所得数值解的侧视图比较 同时还检验了这两种方法的守恒性。表1和表2展示了计算结果的质量误差。结果表明格式T2-PC-CFVM可以很好的保持守恒性,而格式 C-FDM-QI 的质量误差超过了3×10-4。图3展示了格式C-FDM-QI和T2-PC-CFVM的计算结果离散总质量随时间的变化。可以看出在T=π/4时刻,与初始总质量相比,C-FDM-QI丢失了大约20% 的质量,而T2-PC-CFVM精确的保持了质量守恒。 图3 格式C-FDM-QI和T2-PC-CFVM所得解的离散总质量随时间的变化 算例2本算例中对陡峭前沿移动问题进行了计算,计算区域为Ω=[-1,1]2。初始条件为 (51) 速度场(β1(x,y),β2(x,y))=(-0.5,-0.5),扩散系数α1=α2=1×10-3。图4展示了M=50,N=100,T=0.8时,不同数值格式 C-FDM-QI,T2-PC-CFVM和近似精确解的比较图。取M=200和N=200的细网格,应用格式T2-PC-CFVM得到近似精确解。由结果可以看出格式T2-PC-CFVM可以很好地近似陡峭前沿,得到的结果与参考精确解基本一致,T2-PC-CFVM的结果均为正值。C-FDM-QI 在陡坡前沿移动附近产生强烈的震荡,不能准确地近似陡峭前沿且未能保正。 图4 T=0.8 时刻的参考精确解和不同格式所得数值解(见算例2) 本文给出了求解对流占优扩散方程的时空二阶保正守恒格式。沿特征线平均得到时间二阶格式。通过带保正约束的守恒插值和局部限制器使得数值解为正值,保持质量守恒且精度不变。数值实验证明了所提方法的性能,并从数值上证明了它们的守恒性和保正性。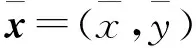

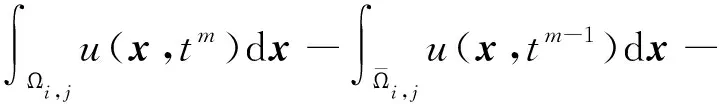
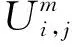
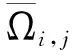
v2(x,y,t)=-α2(x,y)uy(x,y,t)。
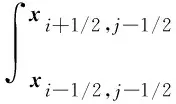



1.2 守恒保正插值

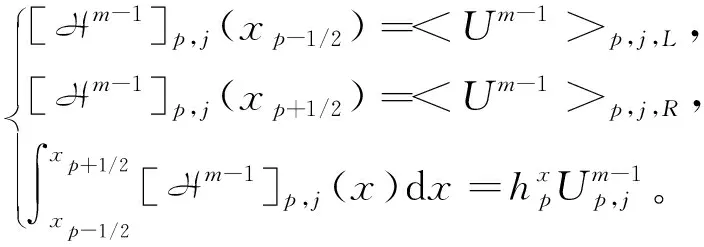
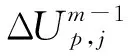
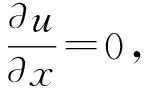
UNx+1,j=UNx,j。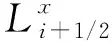




1.3 PPM插值方法保正限制器
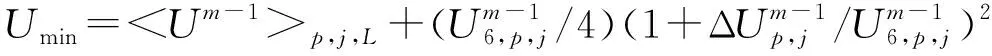
1.4 守恒保正局部限制器


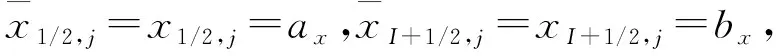

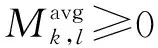
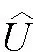

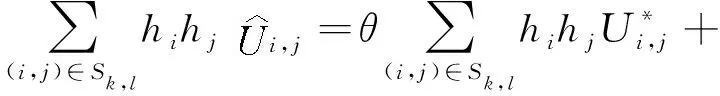
2 格式性质


3 数值算例




4 结语
