VoIP模式地空通信数据链信号特征量识别算法

吕方舟

(中国民用航空西北地区空中交通管理局 宁夏空管, 银川 750000)

0 引 言

随着我国航空业的飞速发展, 地空通信数据链系统逐步成为地空数据传输的主要方式, 在航空运输方面起到了巨大作用[1]。互联网语音协议(VoIP: Voice over Internet Protocol)模式在地空通信数据链中的应用, 最大限度降低了语音通信引发的语音歧义, 增强了飞行员与管制员的交流成效, 对飞机的远程操控、 空中交通管理等工作提供了极大便利[2]。面对复杂的空中环境, 为确保地空通信数据链信息交换顺利进行, 对其信号特征量的识别变得尤为关键。

张林锋等[3]利用小波包分解方法采集振动信号, 在此基础上构建时频矩阵, 并依据Fisher的判断选择奇异值作为振动信号特征量。卢俊等[4]以爆破振动信号与岩体破裂信号数据为目标, 分解两类微震监测信号, 若得到窄带本征模态分量, 使用相关系数法确定与两类原始信号最相关的分量, 计算各主分量近似熵, 将主要分量的近似熵值构成表征微震信号的高维特征矢量作为支持向量机的判断输入实施训练预测。

以上方法操作范围有限, 均无法应用于地空通信中。笔者提出一种基于粒子群和减法聚类的数据链信号特征量识别算法。通过信号特征提取与信号特征量建模, 确定整体信号特征状态, 融合粒子群与减法聚类方法, 完成高精度信号特征量识别任务。

1 数据链信号特征提取

为获得准确的数据链信号特征量数据, 首先提取数据链信号自身特征。数据链信号调制样式即为信号的关键特征, 根据数据链独有特点可知, 需要提取的调制样式有单边带SSB(Single-Sideband Modulation)、 频移键控FSK(Frequency-Shift Keying)、 最小频移键控MSK(Minimum Shift Keying)。针对情况各异的信号特征, 其时域包络特性也各不相等。频率调制信号类型属于恒包络调制[5], SSB信号包络是不断改变的, 因此将包络改变作为信号区分的权衡点。包络改变强度变量R的计算公式为

R=σ2/μ2

(1)

其中μ为信号包络平均值,σ2为信号包络方差。此变量可反应出信号包络浮动高低, 完成恒包络与非恒包络信号划分。

信号频域具备大量信息, 在提取过程中主要包含载频、 带宽和码元速度3个基础变量。多数地空通信数据链信号的调制类别是FSK, 将FSK信号解析式记作

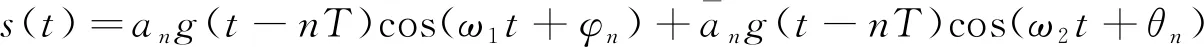
(2)

关于FSK信号, 其二进制基带信号功率谱为

PE(f)=fsP(1-P)[G1(f)-G2(f)]2

(3)

其中G1(f)与G2(f)均为符号频谱,P为符号出现的几率。

使用求平方谱手段, 对FSK信号采取平方计算, 同时去掉计算过程中的常数项, 得

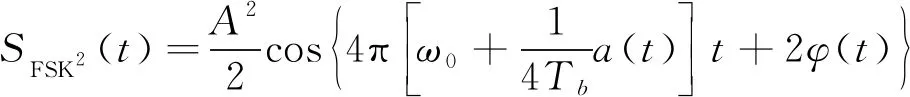
(4)

若VoIP模式地空通信数据链信号初始时段相位为φ0, 通过近邻码元间的对应关联, 在随机时段, 码元原始相位和信号初始时段码元相位间的差值为π的整数倍, 即φn=φ0±kπ, 则

(5)

由此将式(4)变为

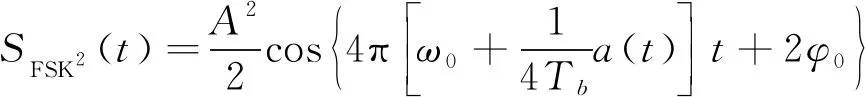
(6)

在计算中排除了FSK信号的相位跳变情况, 仅需求解出信号两个频点2f1、2f2, 就能获得准确的数据链信号载频、 频偏等特征。

2 小波能量谱下数据链信号特征量模型构建

将提取获得的数据链信号记作x(t), 则x(t)的持续小波变换流程为

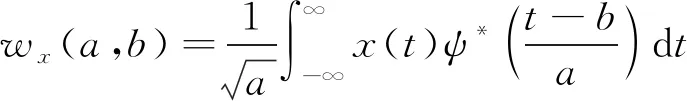
(7)

其中*为共轭,ψ(t)为小波函数。

小波变换原理是两个希尔伯特空间的等距离转换, 在实际操作中, 需要离散化尺度a与移动因子b, 得到的基于二进制离散栅格的小波变换为

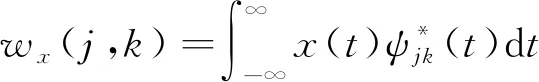
(8)

若地空通信数据链信号共有L种, 每种训练样本数量为Pj, 为剔除随机元素不良影响, 对不同信号样本的尺度-小波能量谱采取类内均值计算。设定第j种信号的类均值小波能量谱为Ej(f), 推算间距Ej1j2(f)数值, 获取各类信号样本类间的能量谱差别数据。为准确分析信号特征量性质, 代入展现信号特征分布的λ水平能量聚点理念[6], 构建基于小波能量谱的数据链信号特征量模型, 大幅增强下一步信号特征量识别的精准度。

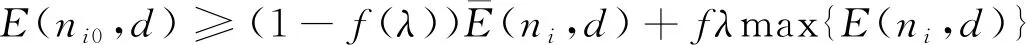
(9)

约束条件, 则点ni0Ts即为信号x(n)处于d尺度的一个λ水平能量聚点。其中f(λ)为λ处于0～1区间的单增函数,f(λ)能根据具体情况调整λ水平的敏感度。假如f(λ)=λ, 可得

(10)

值得注意的是, 尺度功率均值、 最高值能依据先验知识得到。实际操作中,λ水平能量聚点内的能量与功率不一定拥有真实物理意义[8], 使用该能量聚点完成对固定特征在对应区域聚集程度的量化分析。

针对VoIP模式地空通信数据链的不同类型信号, 其类均值小波能量谱间的差异使用方差D(f)描述, 再通过距离或方差挑选特征量。信号特征分布多数呈现不匀称形态, 使用能量聚点策略对信号分布水准进行实时剖析。

经研究可以发现, 能量谱差别多数点一般汇聚或重合在某类固定频段。因此挑选靠近具有高λ水平的能量聚点作为特征矢量, 不但可以了解能量内部信息, 还提高了特征矢量维数, 通过消除多余分量, 大大地减少模型复杂性[9]。聚类分析初始阶段, 在能量谱差异明显的频段, 各个类均被聚类中心替代, 确保类间差异化数据的完整性, 并有效压缩信号特征。聚类的根本目标是考虑能量处于尺度因子a直线内的分布特征, 聚类方法运用R型聚类策略, 使用明氏距离进行计算变量值, 则有

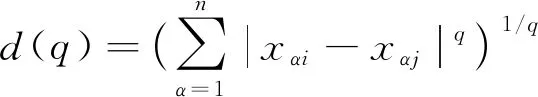
(11)

距离对参变量q的敏感性较强, 尽可能将q值设定成较小值。最后得到小波能量谱下数据链信号特征量模型为

(12)

3 基于粒子群和减法聚类的数据链信号特征量识别

通过上述可以确定数据链信号特征量分布情况。下面融合粒子群与减法聚类手段, 设计一种数据链信号特征量识别算法, 获得高品质信号特征量识别结果, 确定数据链信息交换实时状态, 保证地空通信安全快捷传输。

粒子群算法在迭代过程中, 粒子利用过往记忆追踪两个极值更换自身状态[10], 两个极值依次为个体极值点与全局极值点。将粒子更换自身速率与方位的解析式分别记作

(13)

(14)

其中ω为权值因子,t为迭代数量,r1、r2为匀称分布与0～1区间内的任意值,c1、c2为学习因子。粒子在搜寻空间追踪Pi与Pg, 直至实现预期的迭代数量或符合规划的适应值偏差阈值。

减法聚类就是设定每个数据点均为密度聚类中心。将每个数据点均当作聚类中心待挑选目标, 则数据点xi位置的密度指标为

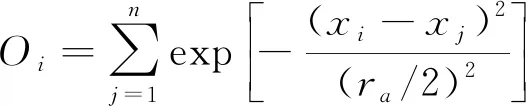
(15)

其中ra为位置半径, 表示信号点的相邻区域。若数据点xi周边具有若干相邻数据点, 则xi拥有高密度属性。设xcl为选择后的聚类中心点,Ocl为数据密度指标, 则各数据点xi的密度指标使用

(16)

进行修改。其中rb为密度指标明显降低的范围, 一般rb值会高于ra, 防止产生距离十分接近的聚类中心, 通常rb=3ra。由此看出, 接近首个聚类中心的xc1数据点密度指标会慢慢变小, 导致此类点无法被选为下个聚类中心。

因此需要调整每个数据点的Ocl, 将聚类中心更换为xc2[11]。重复执行该流程, 在确定第k个聚类中心后, 使用

(17)

修改数据中心的密度指标。其中xck为第k个聚类中心,Ock为聚类中心密度。

在地空通信数据链信号特征量识别过程中, 因为星座图重建是在基带信号基础上完成的, 利用星座表实施特征量识别时, 采用信号载波频率进行下变频转换, 再使用笔者设计的基于粒子群与减法聚类相融合的策略完成高精度信号特征量识别。

运用减法聚类重建星座图[12], 各类阶数的调制手段和不同的最优经验聚类半径相对应。在笔者方法中, 采用聚类半径作为粒子群内的粒子, 迭代过程运用减法聚类获得的重建星座图推算粒子适应度, 确定粒子最佳解与全局种群的最佳解, 并更新粒子速率与方位。迭代停止后获得最终的整体最佳解作为最优聚类半径, 依据获取的聚类半径完成特征量评估识别。粒子群适应度函数为

(18)

其中i为不同类型的调制模式,M为减法聚类获得的聚类中心数量,Mci为预期星座图内点的数量,R为减法聚类重建后星座图最远与最近聚类中心的比值,Rci为对应调制模式的预期值, |C41|为信号的四阶积累量绝对值, 一般情况下该值等于0, 表明重建星座图相对的四阶积累量绝对值越低, 重建星座图和地空通信数据链信号的预期星座图越接近。适应度函数变量的理论值如表1所示。

表1 适应度函数变量的理论值

表1中QAM(Quadrature Amplitude Modulation)为正交振幅调制。设定获得的地空通信数据链信号特征量数据集为(x1,x2,…,xn), 则笔者方法信号特征量识别过程如下。

初始化粒子群的群体规模为6个粒子, 每个粒子处于[0.06 0.5]间的任意数值, 种群数据为25, 初始化权值为0.6, 学习速率为0.46与0.25, 迭代数为0； 针对每个粒子相对的聚类半径依据上述内容实施减法聚类, 得到粒子适应度； 根据适应度更新粒子后计算对应的速率与方位, 设定k=k+1, 若k<25, 重新进行减法聚类操作, 反之终止迭代, 输出最佳聚类作为最终的信号特征量识别结果, 完成识别工作。

4 仿真实验

为证明笔者方法识别可靠性, 使用笔者方法、 文献[3]与文献[4]方法进行仿真实验。设定信号载频为440 MHz, 码长为12 bit, 码长为11 bit, 信号调制指数变化区间为0.3～3, 步长为0.2。选择700个数据链信号样本, 使用3种方法识别信号特征量, 具体准确识别率如图1所示。

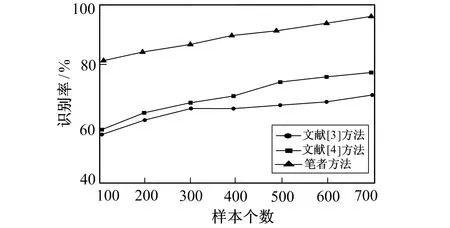
图1 3种方法识别率伴随训练样本个数的改变情况

由图1可看出, 在样本数量小于300组的情况下, 文献[3]与文献[4]方法的信号特征量识别精度相差较少, 约为3%, 但在高于300组时, 文献[3]中的方法识别精度逐渐降低, 文献[4]中的方法识别率保持在70%左右。而笔者方法从实验初期就一直保持较高的识别精度, 不会因为样本数量的变化导致方法的稳定性变差。这是因为笔者方法使用粒子群与减法聚类相融合策略, 通过聚类半径实现精确的信号特征量识别任务。

根据图1的实验结果, 挑选35个样本进行信号特征量识别, 其余样本为测试集, 得到不同信噪比情况下, 识别率和特征量数值变化曲线, 如图2所示。

由图2可知, 与两种文献方法相比, 笔者方法能获得相对优秀的信号特征识别精度。在特征量高于20时, 准确识别率处于稳定状态, 信噪比高于0 dB情况下, 笔者方法识别率高达96%, 且不会受到噪声变化的干扰。由此看出, 笔者方法拥有良好的抗噪性能, 可以在复杂多变的VoIP模式地空通信中提供优质的信息交换服务, 为地空之间的顺畅通信提供重要参考。

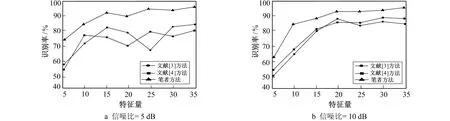
图2 不同信噪比下3种方法的识别率对比

5 结 语

为完善VoIP模式地空通信数据链信息交互流畅性, 笔者提出基于粒子群和减法聚类的数据链信号特征量识别算法。该方法运算简便、 可操作性强, 利用定量计算确定信号特征量, 防止出现识别结果的主观性偏差, 实现高质量识别目标, 在航空语音实时传输方面发挥更加突出效用。