有效数字修约运算疑难点的探讨
2022-08-12孔祥威金爱蝶徐蕾蕾章美琪
孔祥威,金爱蝶,徐蕾蕾,章美琪
(1.浙江工贸职业技术学院,浙江 温州 325003;2.温州佳合标准化信息技术事务所,浙江 温州 325200)
在教学研究中,会产生大量的试验数据[1-3],如分析化学、材料分析技术等课程,企业中的测试分析也是如此。由于检测方法和测量仪器精度的不同,造成试验中所得数据的有效数字的位数不同。因此,在试验数据运算过程中,必然会碰到修约问题,这直接影响了测量结果的准确性。然而,有些研究者或刚接触检测分析的大学生,对数据处理不严谨,造成数据记录和处理的不规范,甚至错误的情况,亟须引起关注和重视[4]。
在日常检测分析的教学与科学研究中,有效数字修约是紧密围绕着标准开展的[5-6]。标准是企业、科研机构等开展有效数字修约的依据,是修约规则得以应用的基础和桥梁[7-8]。如GB/T 8170-2008《数字修约规则与极限数值的表示和判定》中明确有效数字修约的适用范围及修约规则;GB/T 228.1-2021《金属材料拉伸试验第1 部分:室温试验方法》等产品标准明确结果的保留位数。然而,有些分析研究人员没有充分理解标准中的条款要求,对于标准适用范围、修约间隔等缺乏清晰的认识,与此同时,对于标准中没有明确规定的内容有时会无从下手,如有效数字的运算规则等,这需要在标准的基础上借助经验法则(rules-of-thumb,ROT法则)来运算与修约[9]。
因此,以标准为指引,借助ROT法则对有效数字修约规则适用性、数据处理过程、结果判定等方面内容进行全面系统的探讨分析,提高在检测分析中检测结果的准确性和判定的合理性,以此提高学生开展检测分析任务的能力,也为研究分析工作提供科学的参考。
1 标准与有效数字修约的关系
1.1 标准
《中华人民共和国标准化法》指出:“标准是指农业、工业、服务业以及社会事业等领域需要统一的技术要求。国家鼓励采用推荐性标准。”这明确了标准在我国经济社会发展中的重要地位。在GB/T 1.1-2020《标准化工作导则第1 部分:标准化文件的结构和起草规则》中对“标准”进行了定义:通过标准化活动,按照规定的程序经协商一致制定,为各种活动或其结果提供规则、指南或特性,供共同使用和重复使用的文件。生产生活中的规则、制度都是标准的一种形式。当今,标准已成为世界各国通用的语言,世界需要标准协同发展。因此,企业在开展生产、检测、销售过程中,标准是其开展活动的基础。
1.2 标准与有效数字修约
在GB/T 8170-2008的基础上,相应的产品和产品检测标准中,一般也会明确有效数字的舍入要求和指标限制。标准是检测分析的依据,如何运用标准进行数据运算与结果判定是检测分析准确的关键。因此,不管作为科研工作者、企业检验员,还是大学生,当开展检测分析等相关工作时,很有必要结合相关标准对有效数字修约进行全面理解,这样才能保证检测结果的准确性和判定的合理性。
1.3 经验法则(ROT法则)
在GB/T 8170-2008等标准中没有明确有效数字的运算方法,但在很多文献、书籍、维基百科中却经常被提及[9-11],这就是通常所说的ROT 法则,即运算得到的结果不能比开始运算时得到的数字更精确。下面举例说明ROT法则在四则运算应用中的几种情况。
1.3.1 加减运算规则
当多个有效数字进行加减运算时,有效数字的和或差应当以有效数字中小数点后位数最少的数字(绝对误差最大)为准。如例1所示,不管是先修约再计算,还是先计算后修约,都是允许的,结果都是以小数点位数最少的数字为准。
例1:21.456+24.153 48-22.37
解法1:先将算式修约为21.46+24.15-22.37,最后结果为23.24。
解法2:先算出结果23.239 48,再修约至23.24。
1.3.2 乘除运算规则
当多个有效数字进行乘或除时,所得到的积或商以有效数字位数最少(相对误差最大)为准。如例2 所示,不管是先修约再计算,还是先计算后修约,都是可以的,但是结果都以有效位数最少的数字为准。
例2:0.482×0.1238×2.28
解法1:先统一修约为0.482×0.124×2.28,最后结果修约为0.136。
解法2:先算出结果为0.136 051 248,最后结果修约为0.136。
2 有效数字修约的疑惑点探讨
2.1 有效数字修约的适用范围
在实际的检测分析中,到底要在什么情况下使用“四舍五入”,什么情况下使用“四舍六入五成双”,会让很多人感到疑惑,特别是初次接触检测分析的大学生。
GB/T 8170-2008 中明确提出,“四舍六入五成双”是适用于科学技术与生产活动中测试和计算得出的各种数值。因此,不管是做科学研究,还是企业的生产检测活动,当所得数值需要修约时,都应按该标准的要求进行。
2.2 有效数字的修约间隔
在GB/T 8170-2008中定义修约间隔是指修约值的最小数值单位。如指定修约间隔为0.1,修约值应在0.1的整数倍中选取,相当于将数值修约到1位小数。如指定修约间隔为100,修约值应在100 的整数倍中选取,相当于将数值修约到“百”数位。
以上几种情况在平时运算中是比较常见的,标准中还提及了两种比较不常用的修约间隔,分别是0.2 和0.5 的单位修约。如在GB/T 228.1-2021 中明确,屈服点延伸率应修约至0.1%,其他延伸率和断后伸长率应修约至0.5%。现分析如下:
(1)0.5单位修约过程。将需要修约的数字α乘2,得到数值2α,将2α运用“四舍六入五成双”规则修约至个位,所得结果2α修约值,2α修约值除以2得到α的修约值,具体修约过程如表1所示。
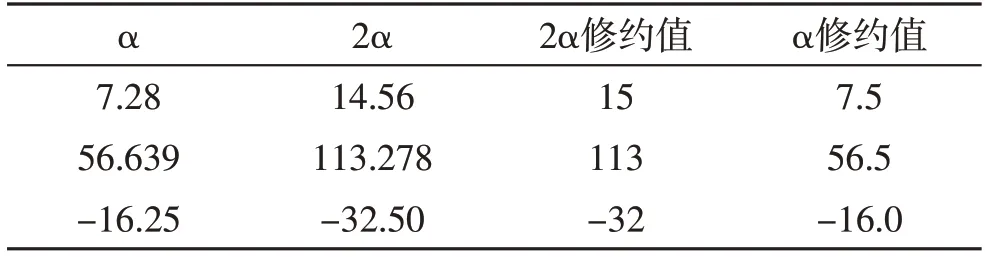
表1 0.5单位修约规则应用(修约至个位)
(2)0.2单位修约过程。将需要修约的数字β乘5,得到数值5β,将5β运用“四舍六入规则”进行修约,所得结果5β修约值,5β修约值除以5 得到β的修约值,如表2所示。
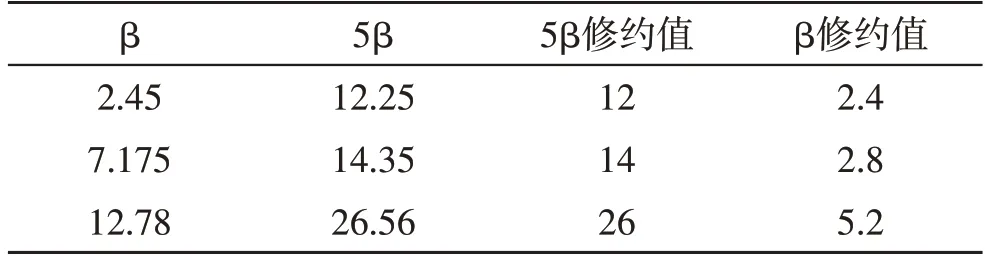
表2 0.2单位修约规则应用(修约至个位)
因此,按标准GB/T 228.1-2021 规定,假设断后伸长率为17.51%,按0.5 单位进行修约计算,现得两倍修约值为35%,最终结果为17.5%。
2.3 有效数字连续修约问题
GB/T 8170-2008规定,数字修约时,应在明确修约间隔和修约位数后,一次性修约到位,不可进行多次连续修约,否则很可能会造成数值偏大或偏小。
标准中也指出,“在具体实施中,有时测试与计算部门先将获得数值按指定的修约数位多一位或几位报出,而后由其他部门判定。”因此,在修约中也可多保留一位数字,以便最后修约成所要求的位数,这是符合标准要求的。比如,对数值23.1234 修约至个位,可以先将报出值修约至23.1+(数值右上角加“十”或加“一”或不加符号,分别表明已进行过舍、进或未舍未进),最后修约至23。在这种精度允许的情况下,在运算过程中,可将数值修约多报一位或几位,但如果数值本身的测量精度只是个位,就不适合再增加一位。
2.4 计算结果值的表示与判定
GB/T 8170-2008中明确指出,在判定测定值或其计算值是否符合标准要求时,应将测试所得的测定值或其计算值与标准规定的极限数值作比较,比较的方法可采用全数值比较法和修约值比较法。同时,GB/T 8170-2008 还规定,当标准或有关文件中,若出现对极限数值无特殊规定时,应该采用全数值比较法;如规定采用修约值比较法,应在标准中加以说明。
2.4.1 全数值比较方法
全数值比较法是将检测值不经修约处理(或虽经修约处理,但应标明它是经舍、进或未进未舍而得),用该数值与规定的极限数值作比较,但是只要超出极限数值规定的范围,则都判定为不符合要求。
2.4.2 修约值比较法
修约值比较法是将测定值或者对它进行修约,且修约数位应与所规定的极限数值数位一致。同时将修约后的数值与规定的极限数值进行比较,只要超出极限数值规定的范围都判定为不符合要求。
因此,要对某个产品的结果值进行判定时,要找到相应的检测方法标准,严格依据标准上的要求进行判定。如GB/T 1196-2017《重熔用铝锭》明确规定,成分分析的判定应采用数值修约法。如GB/T 5009.5-2010《食品中蛋白质的检测》,没有规定相应的修约规则,则应该按照全数值比较法,但是该检测方法规定了结果的保留位数,那么实际的检测结果应该按照该方法的保留位数要求进行修约,最后将该结果与产品的指标值进行比较。
3 有效数字修约与运算的难点探讨
在检测方法标准和产品标准中一般会提及检测结果的修约要求,但关于有效数字的四则运算在GB/T 8170-2008及其他产品、检测标准中没有明确提出。因此,关于如何进行有效数字的混合运算、数据处理等难点问题,下面将结合标准和ROT 法则,以实例的方式进行探讨分析。
3.1 运用标准和ROT法则指导下的常见混合运算
关于有效数字的混合运算,是比较容易混淆的。事实上,混合运算只要遵循运算规则即可,即“先乘除后加减,有括号先算括号”的原则。
关于混合运算,现以GB/T 5009.5-2016《食品安全国家标准食品中蛋白质的检测》的第一法(凯氏定氮法)为例,来说明混合运算的规则,下面列出了食品中蛋白质含量的计算公式。
试样中蛋白质的含量按式(1)计算:

式中X为试样中蛋白质的含量,单位为克每百克(g/100g);V1为试样消耗盐酸标准滴定液的体积,单位为毫升(mL);V2为试样空白消耗盐酸标准滴定液的体积,单位为毫升(mL);c为盐酸标准滴定溶液浓度,单位为摩尔每升(mol/L);0.014 0为盐酸标准滴定溶液相当的氮的质量,单位为克(g);m 为试样的质量,单位为克(g);V3为吸收消化液的体积,单位为毫升(mL);F 为氮换算为蛋白质的系数,各种食品中氮的转换系数;100 为换算系数。
为便于理解,运算中以某品牌牛奶中的蛋白质含量为例,其换算系数F=6.25,同时假设以下数值:取样质量m=25.102 5g,取样体积V3=10.00 mL,盐酸标准溶液浓度c=0.102 4mol/L,空白消耗体积V2=1.00mL,滴定终点体积V1=13.13mL。
根据以上假设的数值,将数值代入式(1)中的蛋白质计算公式,如下:
例3:
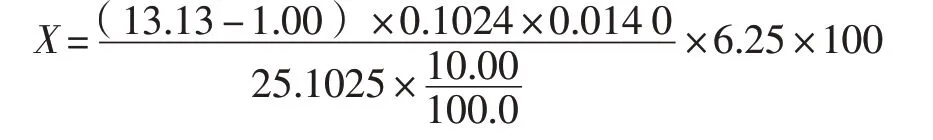
例3 中,由于6.25、0.014 0 和100 为转换或换算系数,其有效数字可看为无限位数,可结合计算式的需要来确定,其有效数字为4 位,取样质量m为6 位有效数字,其他有效数字的位数为4 位。按照ROT法则,当多个有效数字进行乘或除时,所得到的积或商以有效数字位数最少(相对误差最大)为准。所以最终结果的有效数字保留位数为4 位,结果为4.283g/100g+(数值右上角的“+”表明已进行过舍)。
GB/T 5009.5-2010 中明确规定蛋白质含量小于1g/100g 时,有效数字保留至两位;蛋白质含量大于1g/100g 时,有效数字保留至三位。所以按该标准要求,例3的数值运算结果应修约为4.28g/100g。
3.2 运用标准和ROT法则指导下的易混淆混合运算
再来看一种比较容易混淆的情况,在例3 的基础上,假设空白消耗体积V2=1.00mL,滴定终点体积V1=1.05mL,见例4。
例4:

在例4 的混合运算中,括号里的结果为0.05mL,其为1 位有效数字,其他有效数字最少是四位有效数字,最后的运算结果为0.017846828005178。那么依据ROT 法则,最后的结果也应是一位有效数字,计算结果为X=0.02g/100g。因为X=0.02g/100g 的结果误差为ΔX=0.01g/100g,那么含误差的结果可表示为X=0.02±0.005g/100g。由此可见在滴定值(减去空白值后)极小的情况下,运算结果的波动是很大的。
因为运算结果波动大,所以当要运用这样的结果进行判定时需谨慎处理。例4 的结果为0.02±0.005g/100g,当指标要求与检测结果相接近,结果判定很容易引起争议。一般需要变更方法或采用浓缩富集或加大取样量等方法,来保障结果的准确性。比如GB/T 5009.5-2016 第二法(分光光度法)的检测限为0.1mg/100g,要远优于第一法(检测限为8 mg/100g)。因此,当遇到上述的情况时,可以采用第二法来保障结果和判定的准确性。
在结果有效数字保留位数上,GB/T 5009.5-2010中明确规定蛋白质含量小于1g/100g时,有效数字保留至两位,那么依据该方法标准,结果应为0.025g/100g。也就是说,采用ROT法则运算所得的结果满足不了标准方法的要求。事实并非如此,可以观察到,括号中的0.05mL中的5已经是估读值,也就是可疑数字。所以在运算结果中再多取一位,对实际运算结果的帮助并不大。正如前文所述,更重要的是选择一种更适合的检测方法来保障结果的准确性[19]。
通过对以上两种情况的分析,可知有效数字运算需要在ROT 法则和标准的共同指导下运算。然而,在日常检测分析中,为了运算方便,也可直接用计算器算出结果,然后取相应的有效数字位数作为最后的结果。不管作为大学生、老师还是研究者,都有必要去明白有效数字和有效数字运算过程的具体意义,这样有助于对运算结果的理解和运用。
4 结语
本文对标准、有效数字修约、ROT法则的关系进行了梳理与分析,指出标准是有效数字修约的基础与桥梁,ROT 法则是有效数字修约的有益补充。基于标准和ROT法则,对有效数字修约运算中存在的主要疑难点进行分析,在疑惑点上指出:在适用范围上,有效数字修约采用的“四舍六入五成双”适用于科学技术与生产活动中测试和计算得出的各种数值;有效数字的结果报告应以产品或检测标准为准,当没有规定采用何种数值比较法时,则应采用全数值比较法。在难点上指出:混合运算时,运算结果的修约应与标准要求、ROT法则相结合,如果结果的重复性差或相对误差大,应考虑采用更为有效的试验方法来保证结果的准确性。通过有效数字的探讨分析,能够给检测分析员、科研工作者、大学生在实际检测分析中提供参考,从而进一步保障检测结果的准确性和结果判定的合理性、科学性。
