管板设计统一理论（1） ——理论基础简介

朱红松，郑逸翔

（1. 巴斯夫（中国）有限公司，上海 200137；2. 江苏省特种设备安全监督检验研究院，江苏 南京 210036）

管壳式换热器因其适应性，如图1，被广泛应用于石油、化工及核能等诸多工业领域。图1 中S1，S2 代表管板的结构形式， S1，S2 的可能的结构形式及其组合，详见附录A。

由于管板设计的普遍性与重要性， 从20 世纪40年代起管板设计理论便成为力学界所关注的重要课题之一。先驱性的理论研究有Gardner[1-3]、Miller[4]、Duncan[5-6]等，此后其他研究者也做出了重要贡献[7-17]。上述关于固定管板式换热器的研究方法都基于“中面对称”假设，即，假定在两管板中间存在一个与换热管轴线垂直的假想平面，两管板厚度、直径、载荷及周边约束等与该假想平面镜面对称，故仅需分析模型的一半。此外，所有这些方法都只讨论了某些特殊简化条件下，管板为特定结构形式的特定种类换热器的设计方法。

当前，国际及国内压力容器规范[18-22]，关于固定管板式、浮头式、U 型管式换热器管板设计方法都基于上述简化理论。这些规范在一定程度上满足了工业界对管板设计的需求。随着工业实践的迅猛发展，换热器大型化、高参数所导致的紧迫的问题和困难，使得管板的设计需求发生了深刻的变化。现有的简化理论无法处理以下迫切需要解决的理论及实际问题：

（1）现有各种理论或方法[1-17]，他们都从未建立过一个能够将各种换热器联系起来的模型，且兼顾不同结构形式的管板及其组合。

（2）现有规范[18-22]因所采用的假设及简化不尽相同，在一些情况下会导致设计结果的显著差别，但导致这些结果差异的原因尚未分析。

（3）因工艺或实际操作的需求，会导致两管板材料、厚度及管板结构形式不同（参见本文附录A.1节的分析），因而不能满足中面对称假设。

（4）流体压降、管壳程流体自重、换热管自重及管内催化剂重量对薄管板或大直径换热器的重要影响。

（5）换热管弯曲刚度对薄管板或大直径换热器在承受流体压降及换热管自重及管内催化剂重量情形下的重要影响。

（6）管板厚度方向温度梯度、管孔内压力等因素的重要影响。

上述所有问题都与现有理论的通用性及理论精度有关。到2016 年为止，还没发展出一个有极大通用性、高精度的管板设计理论。因此，实践本身要求人们用更严格的精确的理论来检验已经简化了的理论结论，以便使之更加接近于真实，并保证这种简化的结果不至于与真实相去太远，而且也不至于使事情的本质由此遭到忽略。简言之，需要一个新理论来解决这些问题。

从几何的角度考察不同种类的换热器，如图1所示，仅固定管板式换热器在特定条件下（例如，必须要求两管板厚度相等）可满足中面对称条件。若考虑到两管板在材料、载荷、温度、周边约束条件的差异，那么固定管板换热器也难以满足中面对称条件。就几何结构而言，浮头式及U型管式换热器显然不满足中面对称条件。总之，实际情形下换热器通常不满足中面对称条件——载荷不对称或结构不对称或两者兼而有之。因此，必须普遍承认：“中面对称”只是特殊情形，而“中面不对称”则为普遍情形，且“中面对称”亦属于“中面不对称”条件下的特例。

图1 常用类型的管壳式换热器Fig. 1 Common Types of Tubular Heat Exchangers

基于上述观点，朱红松等[23-25]在文献 [24-28]的基础上，采用“非中面对称”的理论架构，发展了一个能够将各种换热器（固定管板式、浮头式及U 型管式换热器）联系起来的模型，且兼顾不同结构形式的管板及其组合，并讨论了更为一般的情形：考虑两管板材料、温度、厚度、直径及周边约束条件不同的情况；考虑换热管弯曲刚度、重力及流体压降、管板厚度方向温度梯度、管孔内压力等重要因素的影响。本文的目的是简要介绍文献 [23-25]的理论基础及适用范围。

1 统一理论的基础

典型立式换热器，如图2 所示，各元件的几何参数、广义外力、内力（力矩、力、剪力）及广义位移（位移、角位移）的正方向、重力方向等业已在图中标明。

图2 立式换热器Fig.2 vertically mounted fixed TS HEX

符号i为下标，i= 1 表示换热器下部相关参数，i= 2 为换热器上部相关参数。共计有WB,ci、WG,ci、Mci、Qci、Nci、Msi、Qsi、Nsi、Mfi、Qfi、Hfi、Mai、Qai、Hai等28 个未知广义内力，它们都表示为单位长度上的力或力矩。

1.1 基本假设

（1）采用弹性薄壁板壳小变形理论；因此前述理论的基本假定将被自动采用，例如，忽略管板厚度方向的正应力及剪切变形。

（2）换热器为轴对称。

（3）两管板均为圆形，但直径、厚度、材料、温度、载荷及周边约束条件等可不同。

（4）换热管分布足够密，因而可视为连续的弹性基础。

（5）换热器内的流场、温度场是稳态的。管板温度场分布只是管板厚度（Z方向）的函数。

（6）管板表面处的压力Pti、Psi为均匀的。

1.2 分析的简化措施

尽管许多次要因素可在理论上加以分析，但为突出理论分析的要点这些次要因素将被忽略，它们是：

（1）管板面内拉力对中间环板横向变形的影响。

（2）一些部件的重力：管板、膨胀节、折流板、附着于管板的催化剂支撑板等。

（3）膨胀节的轴向长度。

（4）换热器支座对壳体或管箱周向变形的约束。

1.3 基本力学模型

统一理论的分析基于如下力学模型：

（1）管板划分为如下三部分（如图2）后分别处理。

① 开孔区（0 ≤r≤a0），以下简称布管区：此区域当量为弹性常数为 、 半径为 实心圆平板。管孔内压力效应采用叠加原理进行处理，详见文献 [24]附录E。

② 环板区（a0≤r≤Rfi），此区域按薄环板处理。

③ 管板法兰环（Rfi≤r≤RTi），此区域按弹性环处理，即，在载荷作用下法兰环截面形心可有转角及径向位移，但忽略法兰环截面形状的变化。

（2）换热管等效为连续的弹性基础，其轴向模量为kW=NtAtEt/ （） ，抗弯模量为kti=FniNtItEt/（），详见文献 [24]附录C。

（3）壳体、管箱按旋转薄壳处理。

2 固定管板式换热器的理论解

由于统一理论采用了“非中面对称”的理论架构，故需对整个换热器进行分析。本节主要介绍管板及部件变形、内力、应力的基本方程。

2.1 布管区当量压力的计算

定义管板挠度wTi为其相对于壳体端部中点处（r=Rm，si）的轴向位移，如图2。管板挠度 与换热管总伸长量 、壳体总伸长量 之间存在如下关系：

其中，δs的计算表达式参见文献 [24]附录A。

换热管总伸长量可分解为：换热管热膨胀δγ，t、换热管自重导致的伸长量δg，t、Poisson 效应导致的换热管伸长量δv，t、换热管因管板作用力导致的伸长量δF，t、换热管内表面轴向摩擦力（因管内流体及填充物）导致的伸长量δft，t及换热管外表面轴向摩擦力（因管外流体）导致的伸长量δfs，t等6 项之和：

管程压力Pti、壳程压力Psi、管子作用力Fti、催化剂支撑板作用力Fxi等，详见文 [24]附录B，作用于管板的总当量压力qTi（r） 为（i= 1，2）：

其中，Pai需按文献 [24]式（B15） 式计算。对实际换热器一般无法给出δft，t、δfs，t、Fxi的精确表达式，故Pai也无法精确计算。文 [24]附录B 理论分析表明，可以用P'ai代替Pai而只在整个结构中导致有限误差的应力分布：

其中，

其中，Wg,ft为单根换热管内所包含的流体及填充物（如催化剂）的重量。

文献 [24]附录B 理论分析表明，Pa1-Pa2的值与δft,t，δfs,t及Fxi无关，其计算表达式如下：

上式中，带下划线项为统一理论导出的新的影响项，而这些项为文献 [26]所忽略。

2.2 管板布管区的挠曲微分方程及其解

布管区（0 ≤r≤a0）在当量压力qTi（r）、单位面积上的换热管反作用弯矩mti、面内拉力Hai及沿管板厚度方向温度梯度作用下，参见文献 [24]附录D，满足如下挠曲微分方程（i= 1，2）：

其中，MΔT,Ti、Δ2MΔT,Ti可按文献 [24]附录D 计算；kai，kbi计算表达式如下：

将式（2）带入方程（5）得，

方程（7）中不带下划线的主项和文献 [26]一致，带下划线的项为统一理论所考虑的附加项（管子弯曲刚度的附加影响）。

方程（7）的解，详见文献 [24]附录C，为：

其 中：C1～C4为 待 定 积 分 常 数；U0、V0为 零 阶Schleicher 函数， 其定义可见文献 [24]附录I ；I0为零阶第一类修正Bessel 函数；参数αk、θ需使得x=·e±2θi满足下述辅助方程，参见文献 [24]附录F.2：

其中，

其中，βk，Bw，Bt，F1，F2表达式如下：

其中，

根据弹性薄板理论，管板转角φTi、径向弯矩Mr,Ti横向剪力Qr,Ti为：

2.3 部件分析

2.3.1 管箱壳体

管板与管箱为整体连接时，参见图3a，定义管箱尺寸参数：aci=RG,ci，am,ci=RG,ci。管箱壳体在Pti、Mci、Nci、Wg,ci、 （即，管箱自重及管箱内流体重力）及热膨胀的作用下，如图2，其边缘径向位移uci及转角φci分别为：

其中， 可由管箱轴向平衡条件求得：

2.3.2 管箱法兰

若管箱与管板为法兰连接，参见图3b，定义管箱尺寸参数：aci=RG,ci，am,ci=RG,ci。这种情况下，可令Mci= 0，Qci= 0 解除管箱壳体对管板的约束。

螺栓力WB,ci垫片反力WG,ci，如图2，作用于管板。其中，WB,ci=/ （2πRB,ci），这里为总螺栓力可按ASME VIII-1-UHX-8 确定。

由管箱法兰的轴向平衡条件可得，

其中，Fs,ci为管箱上支座的支撑力，若管箱上无支座时Fs,ci= 0 。

将aci=RG,ci，am,ci=RG,ci及式（15） 带入式（16a）可得

2.3.3 管板法兰环

无论管板是否兼做法兰，如图2，均定义管板法兰环内半径 为

管 板 法 兰 环 在Psi，Pti，Nsi，Msi，Mci，Mfi，Qsi，Qci，Qfi，Hfi，WB,ci，WG,ci、Nci及热膨胀的作用下，如图2 所示，法兰环截面形心的径向位移ufi及转角φfi分别为：

其中，

注：管箱无法兰时，WB,ci= 0、RG,ci=Rm,ci；管箱配有法兰时，Mci= 0、Qci= 0。

对如图3g 所示的管板与法兰搭焊结构，按文献 [25]附录J 要求调整即可。

2.3.4 壳程壳体

管板与壳体整体连接时，壳体在热膨胀及Psi、Nsi、Msi、Qsi等作用下，如图2 所示，其边缘径向位移usi转角φsi为：

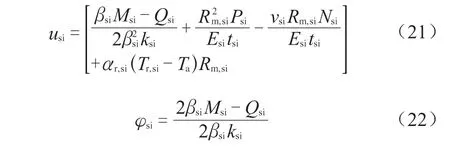
2.3.5 壳程法兰与管板连接

附录A 图3（d）， （e）， （f）， （i）， （j） 给出了典型的壳程法兰与管板螺栓连接的结构形式。通常情况下，固定式换热器不采用壳程法兰与管板螺栓连接结构。但考虑到理论需要，文献 [25]附录B 对此结构做了详细分析并指出了ASME 方法的错误及不足。

2.3.6 中间环板

由文献 [24]附录G，中间环板（a0≤r≤Rfi） 挠度方程为：

其中，MΔT.Ai、MΔT.Ai可按文献 [24]附录D 计算；qAi计算表达式为

其中，A0i、A1i、A2i、A3i（i= 1，2）为8 个待定积分常数。

根据弹性薄板理论，环板转角φAi、径向弯矩Mr,Ai横向剪力Qr,Ai为：

2.3.7 布管区及中间环板的面内拉伸

布管区在Hai、管孔内有效压力Phi及热膨胀的作用下，参见文献 [24]附录E，其径向位移为（0 ≤r≤a0）：

其中，

2.4 待定积分常数及广义内力的求解

Nci，WB,ci，WG,ci可由静力平衡条件及ASMEVIII-1-UHX-8 求解，但其余22 个广义内力仍未知。此外C1，C2，C3，C4，A01，A11，A21，A31，A02，A12，A22，A32，等共计12 个待定积分常数也未知。

以上，总计34 个未知量可用下面的向量表示：

因此，若要求解{Xj} （j= 1, 2, …, 34）则需要获得34 个方程组成的方程组。而这34 个方程可以通过相关元件的协调条件及平衡条件获得。

2.4.1 各元件在连接点处的协调条件

载荷作用下，各元件在连接点处须保持连续，则应满足以下协调条件：

管板法兰环与管箱壳体连接处（r=Rm,ci），将式（13）（18）（19）（14） 分别代入下面的方程：

管板法兰环与壳程壳体连接处（r=Rm,si），将式（21）（18）（19）（22）分别代入下面的方程：

管板法兰环与环板连接处（r=Rfi），将式（18）（32）（26） ～ （28）分别代入下面的方程：

因管板挠度定义为相对于壳体端部中点处的位移，所以

布管区与中间环板连接处（r=ao），将式（25） （8）（26） （10） （29） （31） （27） （28） （11） 及（12）分别代入下面的方程：

自此，我们共计获得32 个方程，要完全求解{Xj}还需2 个独立方程。而管板法兰环的轴向平衡条件，可提供剩余所需的2 个方程。

2.4.2 平衡方程

由管板法兰环轴向平衡条件，可得如下关系式：

2.4.3 广义内力及待定系数的求解

由式（33） ～ （49）所表示的协调条件及平衡条件，令i= 1, 2 可获含34 个方程的方程组。此方程组含34个未知数，故可解。

虽然参数θ，αk，βk，Bw，Bt，F1，F2可用Ha1、Ha2表达，但它们之间不是简单的线性关系，故上述方程组不易直接求解。此种情况下，可先假定Ha1、Ha2的值并计算上述相关参数，于是可将原方程组转化为线性方程组，然后迭代求解。本文用计算机按以下方式迭代求解：

（1）赋予Ha1、Ha2一假定值。

（2）用所假定的Ha1、Ha2值，按本文2.2 节计算参数θ，αk，βk，Bw，Bt，F1，F2的值。

（3）采用步骤（2）计算所得的参数，令i= 1, 2由式（33） ～ （49）可建立含 34 个方程的线性方程组，求解此线性方程组，即可获得{Xj}，其中亦含有新求解的Ha1、Ha2值。

（4）若步骤（3）所得Ha1、Ha2的值与步骤（1）所假定的Ha1、Ha2值相比满足指定的精度要求，则认为解收敛并停止计算。否则，采用步骤（3）所得的Ha1、Ha2值返回步骤（2）重新计算，直至解收敛到指定精度。

大量模拟计算表明，多数情况下2 ～ 3 次的迭代即可获得满足精度的收敛解，因此可求得全部未知广义内力及待定系数。

2.5 部件应力的求解

广义内力及待定系数求解后，按弹性板壳理论，各元件任意点的位移、应力等亦可求解。

2.5.1 管板布管区应力

布管区（0 ≤r≤a0）径向弯矩 可由式（11）确定。据此，布管区上下表面径向弯曲应力为：

布管区（0 ≤r≤a0）径向内力为HTi（r）可由文献 [24] 式（E9）确定，故布管区径向薄膜应力：

布管区上下表面的径向薄膜+弯曲应力：

2.5.2 换热管应力

由文献 [24] 式（B35） 可确定qti（r） ，因此换热管轴向薄膜应力可按下式计算（i= 1， 2）

3 浮头式及U型管式换热器的理论解

浮头式及U 型管式换热器属于典型的“非中面对称”情形，若其符合1.1 节的基本假设，即可按统一理论求解。

3.1 浮头式换热器

这里将讨论如下三种浮头式换热器：

（1）外密封浮头，参见图1c。

（2）内密封浮头，参见图1d。

（3）浸入封浮头，参见图1b。

需再次强调的是，按文献 [23]方法无需假定两管板材料、温度、厚度、直径相同。

3.1.1 对于浮动管板的通用简化

以下讨论假设管板2 为固定端，管板1 为浮动端。

因管板1 为浮动管板，可令膨胀节1 的轴向刚度KJ1→0。此外，对于浮动管板无壳体与之连接，所以可令Rs1=ac1，ts1→0，如此可消除壳体1 对浮动管板的周边约束。

3.1.2 外密封填料函式管板

外密封填料函式管板与壳程壳体之间没有连接，即，壳体1 对浮动管板无约束，所以Qs1= 0、Ms1= 0。

将上述调整后的边界条件代入统一理论，即可求解出两管板及其他相关元件的应力分布。

3.1.3 内密封填料函式管板

由于内密封填料函式管板端部无任何边缘约束，所以需令Qs1= 0、Ms1= 0，Qc1= 0、Mc1= 0 且Nc1= 0。

将上述调整后的边界条件代入统一理论，即可求解出两管板及其他相关元件的应力分布。

3.1.4 浸入式浮头管板

因浮动管箱受Pti与Psi共同作用， 所以Nci，即式（15）需做如下调整：

其中2 （am,c1-ac1），而Δc1ωf,s考虑了壳程流体对管箱的浮力作用。

同样，管箱壳体的径向位移uc1，即式（13）需做如下调整：

此外，管板法兰的径向位移uf1，即式（18）需做如下调整：

将上述调整后的边界条件代入统一理论，即可求解出两管板及其它相关元件的应力分布。

3.2 U型管式换热器

U 型管式换热器，参见图1e，可以视为浸入式浮头换热器的一种特殊形式，即，仅在计算kw时令Et→0 以消除换热管的轴向弹性支撑效应，则固定端管板的应力分布等同于U 型管板的应力分布。

4 统一理论的简要分析

本节将简要介绍统一理论的特点及其独创性。

4.1 基本假设

统一理论采用了尽可能少的假设并使之明确，在此基础上按公理化的方式导出了理论分析的一系列结果，从而保证了统一理论的自洽性及广泛适用 性。

现有各种理论假设多且没有使之系统化、明确化，因此这些理论难以保证其自洽性及广泛适用性。此外，对于同一类型换热器，这些竞争理论的所采用的假设也不尽相同，故在一些情况下采用不同规范会导致设计结果的显著差别。

4.2 换热器间的相互转化关系

基于非中面对称的理论架构，统一理论建立了一个能够将各种换热器联系起来的模型。借助统一理论，我们能够从本质上揭示固定管板式、浮头式及U型管式换热器之间的内在联系以及它们之间的相互转化关系。

4.3 结构适用范围

同样基于非中面对称的理论架构，统一理论为处理不同结构形式管板的组合提供了一个通用的方法，从而彻底解决了此类理论及工程难题。附录A的对比分析表明，统一理论所适用的结构形式远超现有理论，显示了统一理论的巨大优越性。

4.4 载荷适用范围

统一理论考虑了管壳程压力降、换热管自重及管内催化剂重量、流体重力、两管板材料、厚度、温度不同、管板厚度方向温度梯度、管孔内压力等重要因素的影响，满足了高参数、大型换热器的设计需求。

4.5 理论计算的精度

因统一理论采用了尽可能少的假设，从而保证了理论的精度。例如，现有理论认为：重力及压降相对设计压力而言其影响可忽略；换热管弯曲刚度对于管板应力影响非常有限，因而忽略其影响。但统一理论的分析及计算表明，可参见文献 [25]第二、三节，这些因素不但对于大型换热器管板应力有重要影响，同样对于小直径薄管板换热器也有重要影响。

4.6 统一理论与现有理论的关系

管板挠度，参见方程（8），可分解为对称部分及反对称部分 两者之和，

其中，

对于实际换热器，（K1/4α2） ～ （10-2～ 10-4）≤1，因 此θ→ π/4； 并 注 意 到U0（αr, π/4） =Ber（αr），V0（αr, π/4） = -Ber（αr），因此方程 （60） 可简化为

方程（60）、（64）是现有理论[1～22]的基础，因此现有理论可视为统一理论的特殊推论。

4.7 重力及流体压降的影响

与压力载荷相比，重力及流体压降这类非中面对称载荷一般都非常小，因此现有理论都忽略这些因素。但理论分析表明，对于薄管板或大直径管板，这类看似微小的非中面对称载荷对管板应力有重要影响。

对于实际换热器，换热管内表面轴向摩擦力（因管内流体及填充物引起）、换热管外表面轴向摩擦力（因管外流体引起）的分布情况通常无法给出。但这些因素对于非中面对称载荷的计算非常重要。因此，如何正确评估这些因素的影响不但是重要的理论问题，同时也是重要的实践问题。

文献 [24] 附录B.3 通过严密的理论分析，给出ΔPa这一重要参数考虑这些非中面对称载荷的影响，并证明ΔPa取决于以下几项之和，而与摩擦力的分布形式无关：

（a）Pg,t因换热管自重导致

（b）Pg,fs=ωf,sLsχs因壳程流体自重导致

（c）（Pt2-Pt1）χt因管程侧两管板间的压差导致

（d）[Pg,ft+ （Pt2-Pt1） （1 -χt） ]因管内流体及填充物自重及流体压降导致

同时，文献 [24]附录F.5 分析表明，因非中面对称载荷导致的管板径向应力与ζΔPiΔPa（a0/hi）2成正比。因此，对于薄管板或大直径管板，非中面对称载荷的影响不可忽略。此外，文献 [24]附录F.4 ～ F.5还给出了快速评估ΔPa影响的方法。

考虑到重力及流体压降对小直径薄管板或大直径管板的重要影响，笔者将另撰文专题讨论。

4.8 换热管弯曲刚度的影响

方程（7）中带下划线的项，反映了热管弯曲刚度及管板面内拉力的影响。这些因素的综合影响可用参数θ和Ua=βkao体现。

对于实际换热器θ→π/4。当换热器仅承受中面对称载荷（即，ΔPa= 0），此时，考虑热管弯曲刚度对管板的约束会减小管板的变形且有降低管板应力的趋势。但此约束作用非常弱，通常情况下可忽略。

若换热器承受非中面对称载荷ΔPa，文献 [24]附录F.4 分析表明，当Ua=βkao≥3 时，换热管弯曲刚度可显著降低管板应力。文献 [25]3.7 节的算例清楚表明了这一点。

统一理论的分析表明：弹性基础的轴向模量kw对于中面对称载荷有较强的抗力，但对非中面对称载荷几乎没有抗力；而弹性基础的弯曲模量kti则相反，即，其对中面对称载荷几乎没有抗力，但对非中面对称载荷有显著的抗力。

4.9 其他一些问题的解决

现有规范在理论虽都基于中面对称假设，但在未加证明的情况下，这些方法却都被扩展到以下常用但却不满足“中面对称” 的情形：

（1）膨胀节未置于两管板间中央位置，因而不符合“中面对称” 假设。

（2）规范提供了加厚筒体来加强管板的设计方法，它允许两侧加强筒体长度可不同，这显然不符合“中面对称”假设。

（3）通常换热管平均金属温度是沿轴向变化的。考虑一种常见的情形，即，换热管平均温度沿轴线方向单调变化。此时若以中面为基准，虽然中面两侧换热管的长度相同，但中面两侧换热管的平均温度不同，所以换热管相对中面两侧方向的热膨胀不同，即，不能满足“中面对称”假设。

因“中面对称”假设的束缚，此类常见问题在现有理论架构下无法解决。这些因素究竟有何影响是非常重要的实际问题，不应视而不见，必须从理论上给予解答。

借助统一理论，不同条件下这些因素的影响可得到彻底全面的分析。由统一理论可证明，当换热器其他方面满足中面对称条件时，上述3 个因素对计算结果没有影响。但借助统一理论可证明，对于立式换热器，膨胀节与换热器支座之间的位置关系对计算结果有较大影响（笔者将另撰文讨论）。

5 统一理论的验证

文献 [25]选取各种不同类型换热器共计9 个算例，按统一理论求解并与FEA 及ASME 的计算结果做比 较。

所有算例的对比分析表明，统一理论的预测结果与FEA 符合得非常好，而ASME 的计算结果是错误的或不够准确并可能导致不安全的设计结果。

6 结论

当前，以“中面对称”假设为基础的管板设计方法在各国规范中占居主导位置，但此假设极大的限制了这些方法的适用范围且也不能满足实际需求。此外，当代工业所需的越来越多的大型换热器需在严苛且多样的载荷条件下运行，而现有各种设计方法因其固有缺陷也无法保证这些换热器处于合理的安全水平。

基于上述原因，自2016 年来，朱红松等[23-28]基于“非中面对称”的理论架构，系统的创立并发展了管板设计统一理论：考虑了两管板材料、温度、厚度、直径及周边约束条件不同的情况；考虑换热管弯曲刚度、重力及流体压降、管板厚度方向温度梯度、管孔内压力等重要因素的影响。

理论对比分析表明，现有理论为统一理论的简化条件下的推论。各种情形下的数值对比分析表明，统一理论的预测与FEA 符合得非常好，而ASME 的计算结果是错误的或不够准确。

综上所述，统一理论在管壳式换热器设计理论研究方面取得如下突破：

（1）基于“非中面对称”的先进理论架构，统一理论采用了尽可能少的假设，因而能够突破现有理论框架，发展出一个具有极大通用性、高精度的管板设计理论，并将现有理论[1-22]统一到新理论的架构之中。

（2）统一理论建立了一个能够将各种换热器联系起来的模型，且兼顾不同结构形式的管板及其组合，从而保证了统一理论的自洽性及广泛适用性。

（3）统一理论从本质上揭示了固定式、浮头式、U 型管式换热器的内在联系及统一性，并指明了其相互转化关系。

（4）统一理论系统分析了换热管弯曲刚度、自重及压降的影响，为薄管板及大直径换热器的设计提供了坚实的理论依据。

（5）统一理论系统分析了现有设计理论的缺陷及所面临的问题，并提供了解决这些问题的方案，因而能够满足现代工业的需求。

符号、下标及缩写说明

其他未定义符号，参见文献 [25]符号说明（以下给出相关符号的SI 单位）

附录A：换热器的结构形式

常用类型的换热器如图1，其中S1、S2 代表管板的结构形式。本文图3、图4 给出了典型的管板结构形式。

由于统一理论抛弃了中面对称假设，因此统一理论所适用的换热器的结构形式取决于S1 与S2 之间的组合。

A.1 固定管板式换热器的结构形式

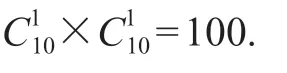
这里需要强调的是，考虑固定管板式换热器两管板任意结构的组合，不仅是理论研究的需要，而且也是基于现实的需求。例如，图5 所示的换热器（一种大型管式反应器），上部管板设计为如图3b 的法兰连接结构以便于装填催化剂，而下部管板则设计为如图3a 的焊接结构。此外，对此类大型管式反应器，换热管自重、管内催化重量及管程流体压降等因素也必须考虑，且最终上、下管板厚度也可不同。

图5 立式安装的换热器Fig.5 Vertically Mounted HEX

A.2 浮头式换热器的结构形式

A.2.1 浸入式浮头换热器的结构形式

A.2.2 外密封浮头换热器的结构形式

A.2.3 内密封浮头换热器的结构形式

A.3 U型管式换热器的结构形式

对于固定管板 S2，图 3a ～ j 所示的结构可采用。因此，U 型管式换热器的可用结构形式为= 10。

A.4 与ASME方法的比较

统一理论与ASME VIII-1 所适用的换热器结构形式对比见表1。表1 的对比表明，统一理论的适用范围远超ASME 及现有规范[18-22]。

表1 换热器适用结构形式的比较Table 1 Comparison of Applicable HEX Configurations

表2 不同管板结构下参数aci，am,ci，asi，am,si 的定义Table 2 Definition of aci, am,ci, asi, am,si for Typical Classes of TS Configuration

这里需特别指出的是，尽管ASME VIII-1 提供了3 种类型浮头换热器的设计规则，但这些规则都是基于中面对称假设，文献 [23-25]的分析表明这种简化处理会导致不正确的设计结果。

本文图3、图4 给出了一些典型的管板结构，但基于统一理论的原理，可以按实际需发展更多的管板结构及组合。这一点体现了统一理论的巨大优越性及广泛适应性。

图3 典型的固定管板结构Fig.3 Typical Classes of TS Configurations for Fixed TS

图4 典型的浮动管板结构Fig.4 Typical Classes of TS Configurations for Floating TS

[10]Galletly， G. D. Optimum Design of Thin Circular Plates on An Elastic Foundation [J]. Pro. Inst. Mech. Eng.， 1959， 173（1）：687-698.

[11]G. B. Boon and R. A. Walsh. Fixed Tube-Sheet Heat Exchangers[J]. Journal of Applied Mechanics， 1964， 31（2）：175-180.

[12]Gardner， K. A. Tubesheet Design： a basis for standardization[C]. First International Conference on Pressure Vessel Technology， Delft， 1969：621-647.

[13]K. Hayashi. An Analysis Procedure for Fixed Tubesheet Heat Exchangers [C]. Proceedings of the Third International Conference on Pressure Vessel Technology： Part 1， 1977：363-373.

[14]Osweiller， F.， 1979，“ Liste bibliographique d’articles and de Codes concernant le calcul des échangeurs de chaleur” -Rapport partiel No. 2 - Etude CETIM 14. B. 03 - 19 Mars 1979.

[15]黄克智， 薛明德， 李世玉. 固定式换热器管板应力的一种建议计算方法[J]. 机械工程学报， 1980， 16（ 2） ： 1-23.

[16]A. I. Soler， S. M. Caldwell， S. D. Soler. Tubesheet Analysis—A Proposed ASME Design Procedure [J]. Heat transfer engineering， 1987， 8（ 3）：40-49.

[17]Osweiller， F.， 2014，“ Criteria for Shell-and-Tube Heat Exchangers According to Part UHX of ASME Section VIII Division 1- ASME PTB-7”， ASME， New York

[18]ASME Section VIII- Division 1-2019[S].

[19]EN 13445—2014[S].

[20]CODAP—2015[S].

[21]PD 5500—2014[S].

[22]GB/T 151， 热交换器[S]. 北京： 中国标准出版社， 2015.

[23]Zhu， Hong-song and Zhai， J. The Unified Theory of Tubesheet Design—Part I ： Theoretical Foundation [J]， Journal of Pressure Vessel Technol， 2022， 144（2）： 021303.

[24]Zhu， Hong-song and Zhai， J. The Unified Theory of Tubesheet Design—Part II： Supplement to the Theoretical Analysis [J].Journal of Pressure Vessel Technol， 2022， 144（2）： 021304.

[25]Zhu， H.， Zhai， J.， and Zhou， G. The Unified Theory of Tubesheet Design—Part III： Comparison With ASME Method and Case Study [J]. Journal of Pressure Vessel Technol， 2022，144（2）： 021305.

[26]Hongsong Zhu. A Unified Analytical Method of Stress Analysis for Tubesheet- Part I： Theoretical Foundation [J]. Journal of Pressure Vessel Technology， 2018， 140（1）：11203.

[27]朱红松. 管板应力精细化分析统一理论简介［J］. 压力容器，2017， 34（ 10） ： 32-42.

[28]朱红松， 翟金国.管板应力分析统一方法的简介（1）—理论基础［J］.化工设备与管道， 2017， 54（2）：8-14.