两重化Buck变换器设计研究

2022-08-12赵立博徐明峰

船电技术 2022年7期

关键词：电感谐波滤波

赵立博，徐明峰，王力

应用研究

两重化Buck变换器设计研究

赵立博，徐明峰，王力

（武汉船用推进装置研究所，武汉 430064）

本文研究两重化Buck变换器的设计方法。在研究基本型Buck变换器的结构和参数计算方法后，得到两重化Buck变换器的结构和主要器件的参数计算方法。在此基础上，基于相同的输入输出设计要求，设计了基本型和两重化Buck变换器，并得到具体的器件参数。通过PLECS仿真软件进行仿真分析，对比了两者的电气性能。仿真结果表明，两重化Buck变化器输出电压和电流纹波小，电流高次谐波含量低，电气性能显著优于基本型Buck变换器。

Buck变换器两重化参数计算主电路设计仿真分析

0 引言

DC-DC 变换器作为重要的一类电源，在现代工业、国防和社会生活领域应用广泛。基本型Buck变换器是一种常用的降压式DC-DC变换器，电路结构简单，便于控制。但是，基本型Buck变换器1的电压和电流纹波大，高次谐波含量多[1]，容易产生较为严重的电磁干扰。

为减少Buck变换器的电压和电流纹波，人们主要从优化控制方式、改进电路结构等方面进行工作。例如，文献[2]提出一种自适应占空比跨周期控制方法，实验结果表明该方法可以获得更小的纹波系数。文献[3]提出一种移相脉宽调制策略，通过调节PWM信号相位抑制特殊次数的电压和电流谐波。利用若干个结构相同的基本Buck变换器适当组合，构成多重化Buck变换器[4]，是一种有效减少变换器纹波的方法。多重化Buck变换器还能有效降低电力电子器件的电流额度，减小滤波器件的体积和重量，提高变换器的可靠性和动态性能[5-6]。

为总结多重化Buck变换器的设计方法，分析多重化Buck变换器纹波的改善效果，本文以两重化Buck变换器为例，研究多重化Buck变换器的设计方法。首先，分析基本型Buck变换器的结构和参数计算方法；其次，分析两重化Buck变换器的结构，并得到两重化Buck变换器主要器件的参数计算方法；再次，基于相同的输入输出设计要求，设计了基本型和两重化Buck变换器，并得到具体的器件参数；最后通过PLECS仿真软件进行仿真分析，对比了两者的电气性能。

1 基本型Buck变换器

基本型Buck变换器拓扑结构如图1所示。图中，Buck变换器包括IGBT模块T1、二极管1、滤波电感f和滤波电容o。直流电源b为Buck变换器供电，o为Buck变换器的负载。

图1 基本型Buck变换器

在开关周期s=on+off期间，对IGBT模块T1施加驱动信号，且在on期间，T1处于通态，D1处于断态；在off期间，T1处于断态，D1处于通态。滤波电感f和滤波电容滤除变换器的高频谐波电流和电压。设=on/s为占空比，s为直流电源电压值，则在电流连续状态，Buck变换器输出电压满足[4]，

基本型Buck变换器滤波电感的电感值计算公式为：

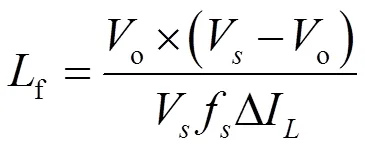
其中，fs=1/Ts为开关频率，ΔIL为电感纹波电流。滤波电容的电容值基本计算公式为，

其中，Δo和Δo分别为变换器输出纹波电压和电流。

此外，选择滤波电容时，需要考虑滤波电容的纹波电流。滤波电容纹波电流的有效值可表示为：

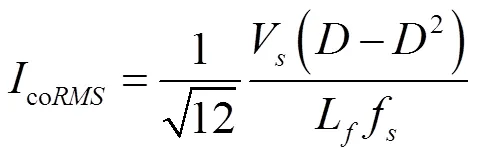
计算得到电容的纹波电流有效值后，按照电容耐流值（如薄膜电容耐流值在70℃条件下为115mA/uF）计算相应的电容值。滤波电容的电容值通常选择式确定值的最大值。

2 两重化Buck变换器

多重化Buck变换器组合若干个结构相同的基本型Buck变换器。图2所示的为两重化Buck变换器，其拓扑结构与图的区别之处，在于增加了一个完全相同的基本变换电路，其中T1、T2是 IGBT，Lf1、Lf2是滤波电感，Co是滤波电容。

工作阶段，T2滞后T1导通，且滞后时间为 Ts/2。在一个开关周期s内，T1和T2的导通时间(Ton)相同，即占空比D 相同。滤波电感f1和f2的电流 iL1、 iL2相位相差s/2、波形完全相同[7]。

图2 两重化Buck变换器

根据两重化Buck变换器拓扑的特点可知，其输出电容的参数计算方法与基本型Buck变换器相同，但滤波电感值的计算方法存在差别。

由于两重化Buck变换器总电流与基本Buck变换器电流纹波比可表示为[6]，

因此，在确定变换器输出电流纹波的条件下，根据式(5)确定基本电路中电感的纹波电流值，再根据式(2)计算基本电路的电感值Lf1和Lf2。

表1给出了Buck变换器的电气性能设计要求，根据上述计算方法，分别得到基本型Buck变换器和两重化Buck变换器滤波电容和电感的数值，具体分别如表2和表3所示。

表1 Buck变换器设计要求

表2 基本型Buck变换器器件参数

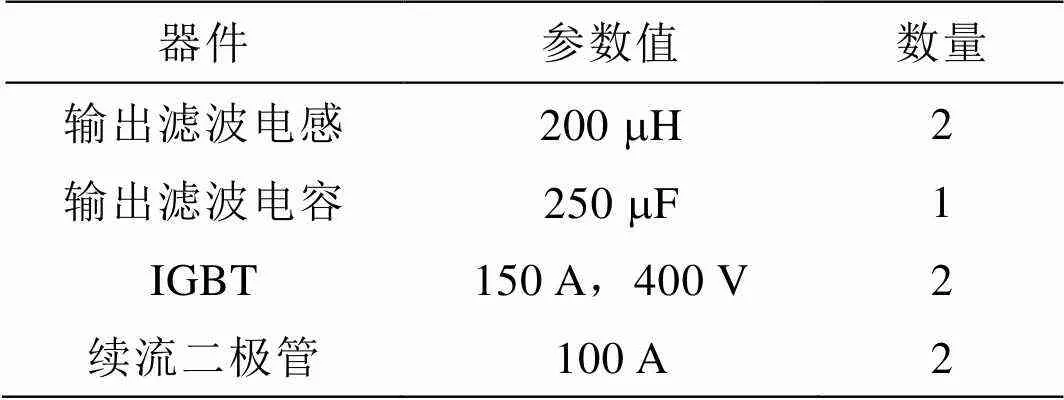
表3 两重化Buck变换器器件参数

表2和表3表明了两类变换器包含器件的数量。可见，两重化Buck变换器包含的器件数量较多。但是，两重化Buck变换器的滤波电感值显著低于基本型Buck变换器，有助于减少电感的体积和重量，提高散热性能。此外，两重化Buck变换器降低了电力电子器件的电流和额度，总体成本得到有效控制。

3 仿真验证

为验证Buck变换器器件参数计算的正确性，对比基本型和两重化Buck变换器的性能差异，下面采用PLECS仿真软件对基本型和两重化Buck变换器进行仿真。

设置仿真时间为0.1 s，仿真步长为开关周期的1/20并采用定步长求解器。

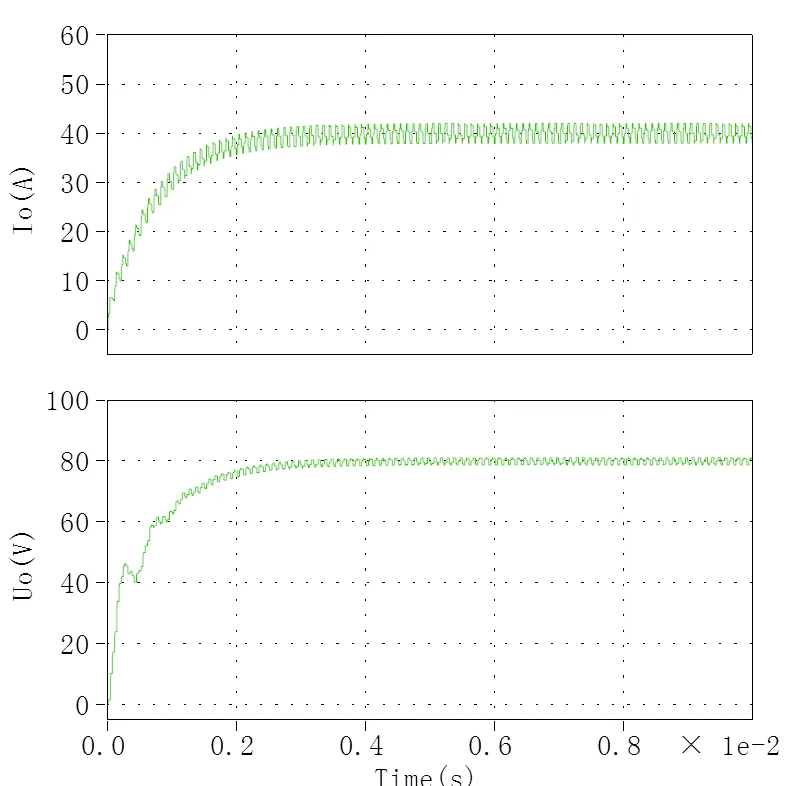
图3 基本型Buck变换器输出电流和电压

基本型Buck变换器全局和局部的输出电压和电流分别如图3和图4所示。两重化Buck变换器全局和局部的输出电压和电流分别如图5和图6所示。由于仿真模型采用开环控制方式，在仿真初期变换器的电压和电流未得到有效控制，但不影响变换器性能的分析。

根据图3、图4、图5和图6，可知基本型Buck变换器的纹波电流为6 A，电压纹波为2.4 V；两重化型Buck变换器的纹波电流为0.1 A，电压纹波为0.2 V。两重化Buck变换器的输出电压和电流纹波分别为基本型Buck变换器的1.67%和8.3%，变换器的纹波得到了有效抑制。

图4 基本型Buck变换器局部输出电流和电压

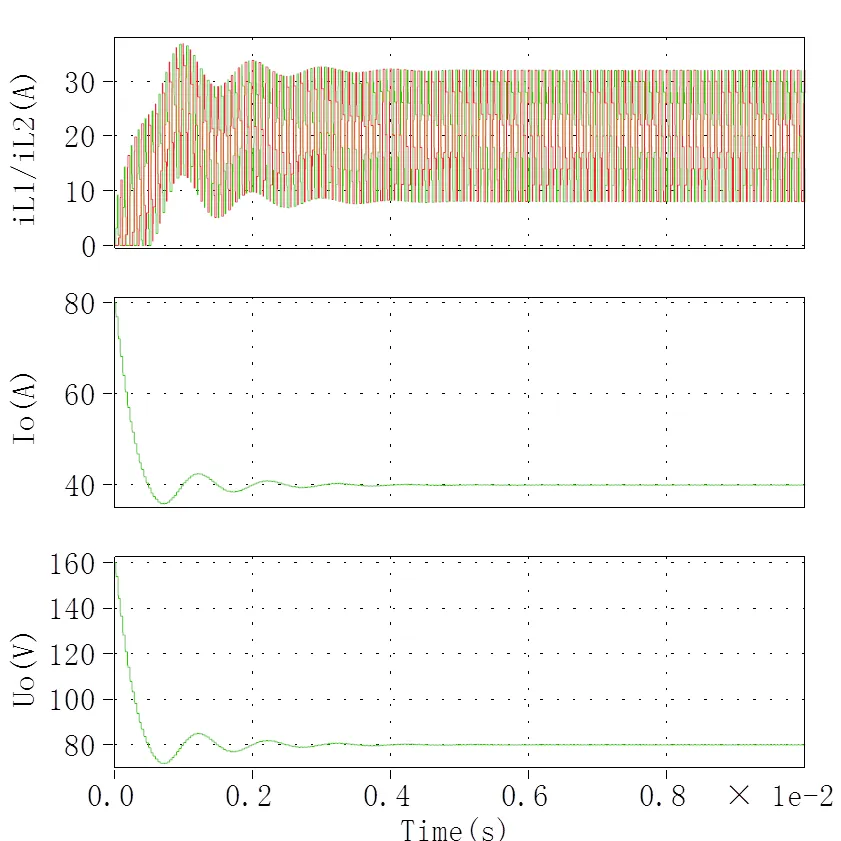
图5 两重化Buck变换器输出电流和电压

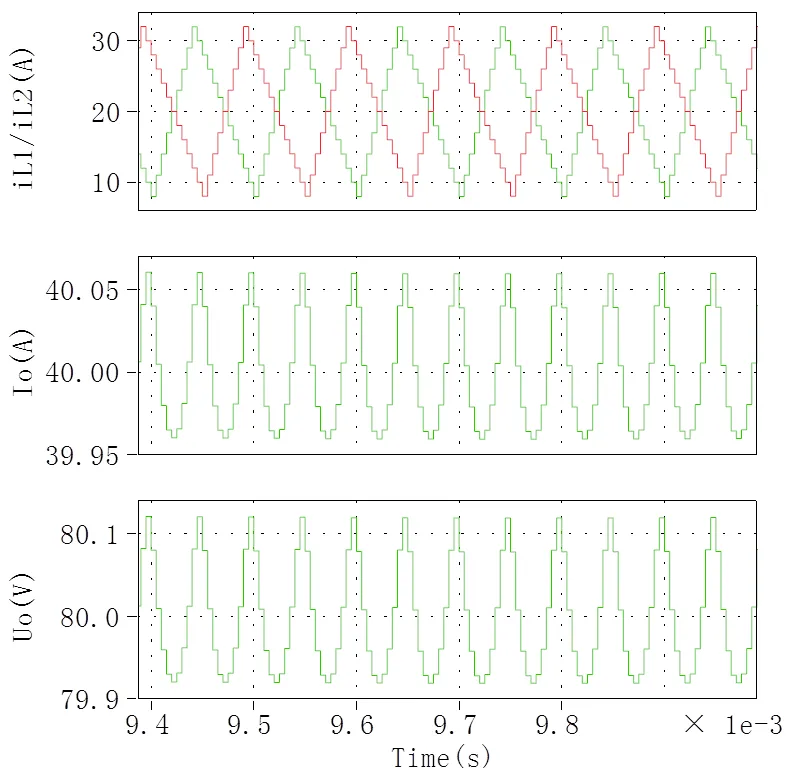
图6 两重化Buck变换器局部输出电流和电压

表4和表5分别分析了基本型和两重化Buck变换器输出电流和输出电压的谐波含量，并着重列出开关频率的倍数次谐波。可见，在相同直流工作点的工作条件下，两重化Buck变换器的谐波电流和谐波电压远小于基本型Buck变换器，且高次谐波分量可以忽略。

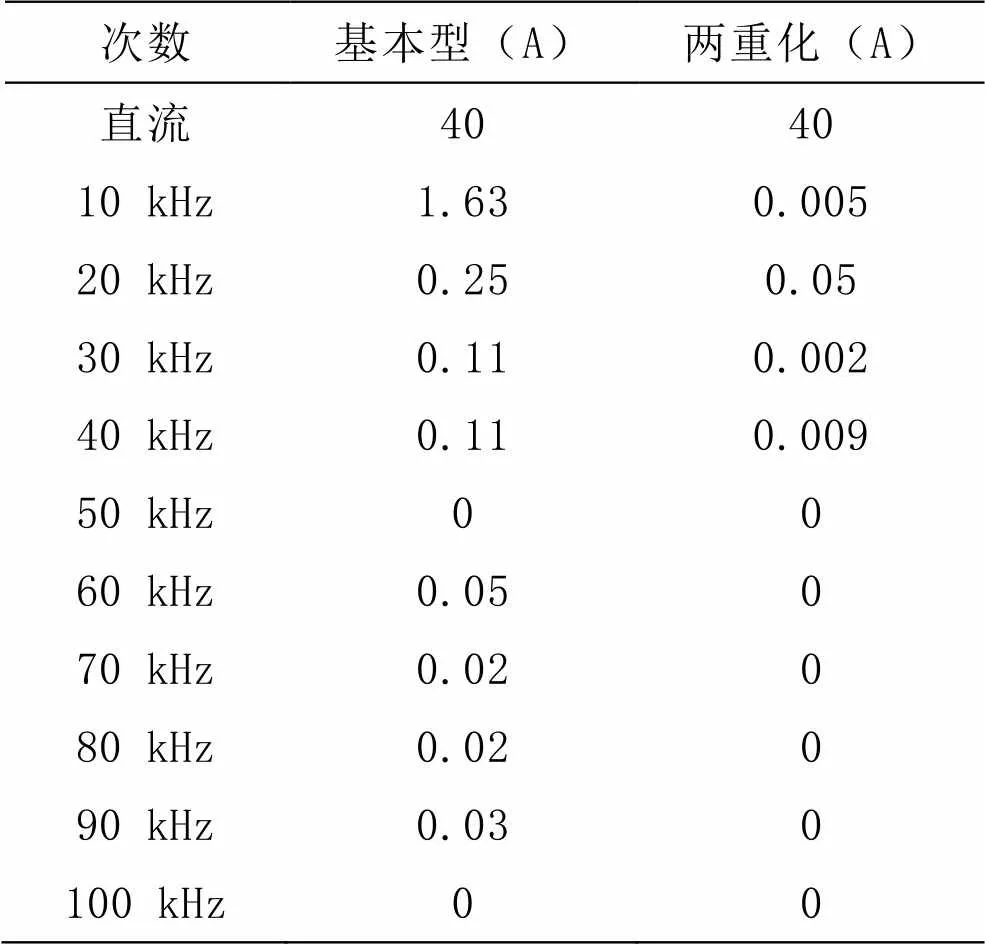
表4 变换器输出电流谐波对比

表5 变换器输出电压谐波对比

4 结论

针对 Buck型 DC/DC 传统脉宽调制输出电压谐波含量较为丰富的问题，提出一种移相脉宽调制策略，对比研究了两种调制策略下输出电压谐波分布情况。通过对理论进行推导和仿真结果进行分析，得出如下结论：移相脉宽调制可以获得更小的输出电压纹波系数；移相脉宽调制与传统脉宽调制下电感电流纹波系数基本相同。

[1] Tao C W, Payed A. Output spectrum analysis of buck converter in DCM with PFM control[C]. IEEE International Sympooium on Circuit and Systems, 2012: 2267-2270．

[2] 李航标, 张波, 罗萍, 等. 开关 DC-DC 变换器的自适应占空比跨周期控制方法[J]. 电子与信息学报，2014，36(9): 2265-2271.

[3] 陈璐珈, 夏益辉, 孙力, 等. 基于 Buck 型 DC/DC 变换器的移相脉宽调制策略[J]. 船电技术, 2018，38(12): 53-56.

[4] 陈坚. 电力电子学—电力电子变换和控制技术[M]. 北京：高等教育出版社，2002:80-81.

[5] Wong P L, Xu P, Yang B, et al. Performance Improvements of Interleaving VRMs with Coupling Inductors[J]. IEEE TPE, 2001, 16(4): 499-507.

[6] 陈明, 汪光森, 马伟明, 等. 多重化双向 DC-DC 变换器电流纹波分析[J]. 继电器, 2007, 35(4): 53-57.

[7] 孙铁成, 郭超, 娜仁图亚, 等. 具有移相控制的ZVS全桥DC-DC斩波变换器[J].电工技术学报，2014, 29(12): 19-24.

Design and implementation of interleaved buck converter

Zhao Libo, Xu Mingfeng, Wang Li

(Wuhan Institute of Marine Electric Propulsion, Wuhan 430064，China)

TM343

1003-4862（2022）07-0046-04

2021-08-26