电机铁芯导热系数测量及影响因素研究

2022-08-12孙良友

船电技术 2022年7期

关键词：铁芯稳态轴向

孙良友

应用研究

电机铁芯导热系数测量及影响因素研究

孙良友

(海装武汉局驻湘潭地区军事代表室，湖南湘潭 411101）

铁芯作为电机的重要组成部分，其导热系数的准确性对电机温度场的计算精度具有举足轻重的作用。针对电工硅钢片在实际使用过程中需考虑叠压效果以及层间绝缘薄膜的影响，不能使用单一材料导热系数作为铁芯的实际导热系数的问题，提出了一种基于稳态法的导热系数测量方法，并搭建了实验平台对电工硅钢片的轴、径向导热系数进行了测量，得到了含硅量、叠压系数、单层厚度等因素对其导热系数的影响规律，并进行了误差分析。实现了对铁芯导热系数的准确测量，为后续电机温度场的准确计算奠定了基础。

电机铁芯导热系数稳态法

0 引言

在先进船舶技术、新能源汽车、高速轨道交通装备、航空航天装备等重点领域，高功率密度电机都是不可或缺的动力核心部件。高功率密度电机运行时，较常规电机热负荷增加，其有限的散热面积更加剧了热量的积聚，并随之产生一系列负面影响。因此细化研究高功率密度电机的温升，并采用高效冷却措施就显得尤为重要。

电机温度场计算本质是求解传热学及流体力学的偏微分方程，其精确性依赖于材料属性与边界条件输入。因此，作为电机设计中主要热力学参数，导热系数的准确性对电机温度场计算精度起着至关重要的作用[1]。

国内外对电机的热计算研究起步较早，但是对于电机中的导热系数的相关研究较少，缺乏统一规范的导热系数标准。1955年，Resenberry等研究者首次使用路的方法对感应电机的转子瞬态停车温升进行了求解，但是其中对导热系数的取用较为经验化[2]。1980年，И.Ψ.菲利包夫对稳态和非稳态负荷下电机的热计算进行了阐述，对于导热系数的设置仍为经验值且不考虑材料的各向异性[3]。近些年来，国内学者也陆续展开了对电机相关材料导热系数的研究。2014年，哈尔滨理工大学的丁树业、邓艳秋等人在其著作中使用热流法测量了电机中常用的环氧树脂等固体绝缘材料的导热系数，并提出了结构不规则的绝缘材料导热系数的间接测量方法[4]。2015年，周秋松在丁树业研究的基础上，再次使用稳态热流法有效解决了交互式固体绝缘材料导热系数的测量问题[5]。2015年，吴尧辉等人利用有限元仿真推导出了电机定子槽部绕组导热系数，计算时考虑了槽满率层间绝缘和浸漆次数等因素的影响，并通过实验对比验证了此等效导热系数的正确性[6]。2017年，国家稀土永磁电机工程技术中心的佟文明等采用无限大平板法对非晶合金铁芯的轴向导热系数进行了实验研究，得到了不同叠压系数下的非晶合金铁芯叠片的轴向导热系数，并以此提高了仿真精度[7]。电机铁芯作为电机重要组成部分之一，其导热系数对电机的温度分布具有很大的影响。但是国内外对于电机铁芯电压硅钢片导热系数的研究较少。

为保证电机温度场计算的准确性，本文以传热、传质学理论为基础，构建了稳态导热系数测量实验平台，测试得到了多种因素下电机硅钢片轴、径向导热系数的变化规律，并验证了该实验方法的准确性，提出了一种准确测量硅钢片导热系数的方法。

1 稳态法导热系数测量原理

目前工程上导热系数的测量对测量仪器有很强的依赖性，稳态法是当前工程上准确度和精确度最高的测量方法[8]，大多数实验是建立在实时监测所研究的物体在加热（冷却）情况下的温度场的基础之上的。傅里叶定律在稳态传热下有：

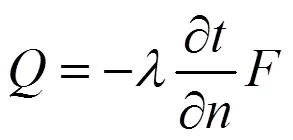
一维温度场导热微分方程式为：

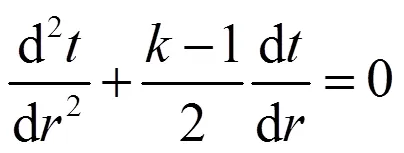
式中：r代表了计算所用坐标系；=1、2、3分别对应于平板试样、圆柱体试样和球体试样；为等温面的法线。式(1)和(2)都是针对热物性不随温度变化的物体，且只适用于固体材料。两式都无通解，但是在具体给定的单值条件下可以求得适用于特定几何形状物体的特解。对于本实验而言，分别采用无限大平板法和圆筒层法进行导热系数的测量，对于平板和圆筒两个形状简单的物体，在第一类边界条件下求解式（2）可以得到以下导热系数的表达式：

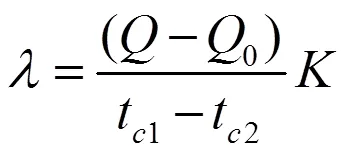
式中：t，t分别为试样冷热面热电偶指示值的算术平均数；为加热器功率；Q为热损失；为形状系数。

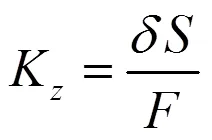
式中：K为轴向导热系数实验中试样（平板状）的形状系数；为叠压系数；为试样的厚度；为传热面积，由试样半径计算。

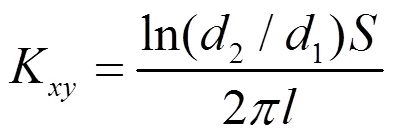
式中：Kxy为径向导热系数实验中试样（圆筒状）的形状系数；S为叠压系数；d1、d2为试样的内外径；l为试样的高度。

每两片硅钢片层间在恒定热流下，温度随厚度变化的示意图如图1所示。两片硅钢层间的接触热阻所带来的温度差为t至t。

现使用传热学基本原理，对本试样在理想状态下的导热系数进行求解计算。当忽略接触热阻时，从1点至5点的热量传递过程在图1中对应为虚线部分（1至5a）。本实验中试样硅钢片总厚度50 mm，每片硅钢片厚0.5 mm，其中绝缘层厚2m，所以硅钢厚0.4996 mm。根据传热学原理有：

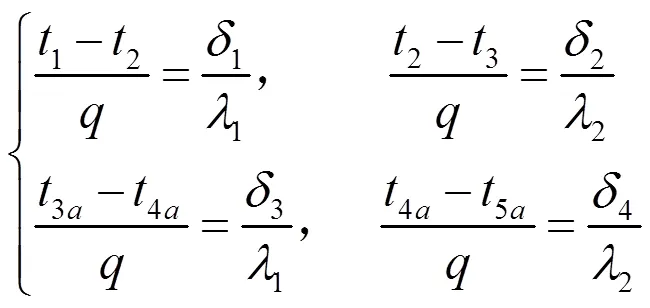
式中：λ、λ分别代表硅钢与绝缘的导热系数，为了计算出不计较接触热阻情况下轴向导热系数的上限，分别取硅钢导热系数35 W/m·K，绝缘导热系数0.1 W/m·K。其效导热系数计算式为：

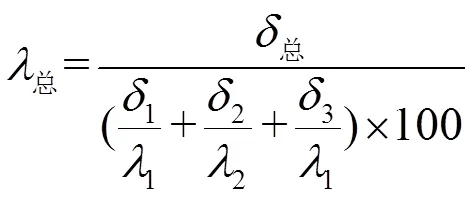
式中：总为试样导热系数，δ总为试样厚度。计算结果见表1：

表1 硅钢片等效导热系数计算

根据表1 计算结果，可以得出硅钢片导热系数随着硅钢片厚度变化曲线图如图2所示。

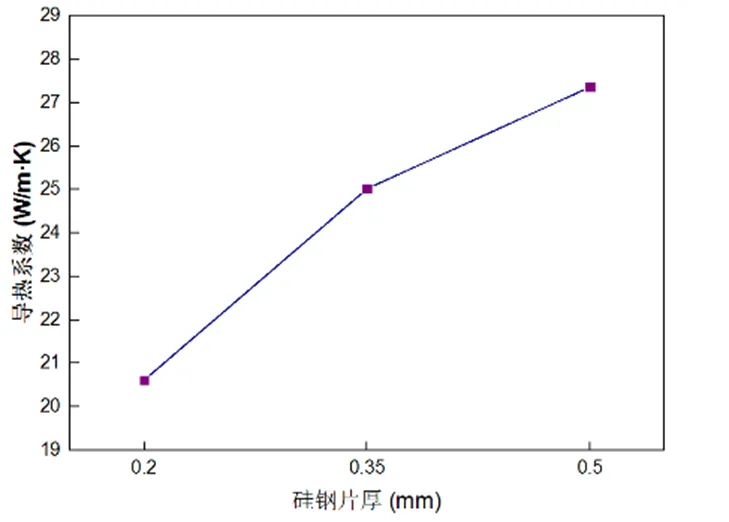
图2 硅钢片导热系数随厚度变化

从图2和表1可知，随着硅钢片厚度的增加导热系数也随之增加，这是由于在绝缘薄膜厚度不变的情况下，单层硅钢片厚度越厚，硅钢所占的比例越大，导热性能就越好。实际情况下，由于存在接触热阻，轴向导热系数实验结果都应低于表1中的结果。实验过程中可以用表1的计算结果验证轴向导热系数实验的正确性。

2 稳态法硅钢片导热系数测量实验

使用稳态法测量不同牌号、不同厚度和不同叠压系数硅钢片的轴向与径向导热系数，为电机温度场精细化仿真提供有效数据支撑。针对电机中使用的电工硅钢片，设计采用稳态平板法和稳态圆筒层分别测量硅钢片轴向和径向导热系数。在保证测量精度的同时又能有较好的经济适用性。

使用Q235试样校准测量装置，以减少接触热阻和热损失带来的测量误差。查阅资料可知，Q235材料在20-200℃时，导热系数为48.2 W/m•K。经过反复验证最终确定电机铁芯硅钢片实验方案。导热系数测量实验装置参数如表2所示。

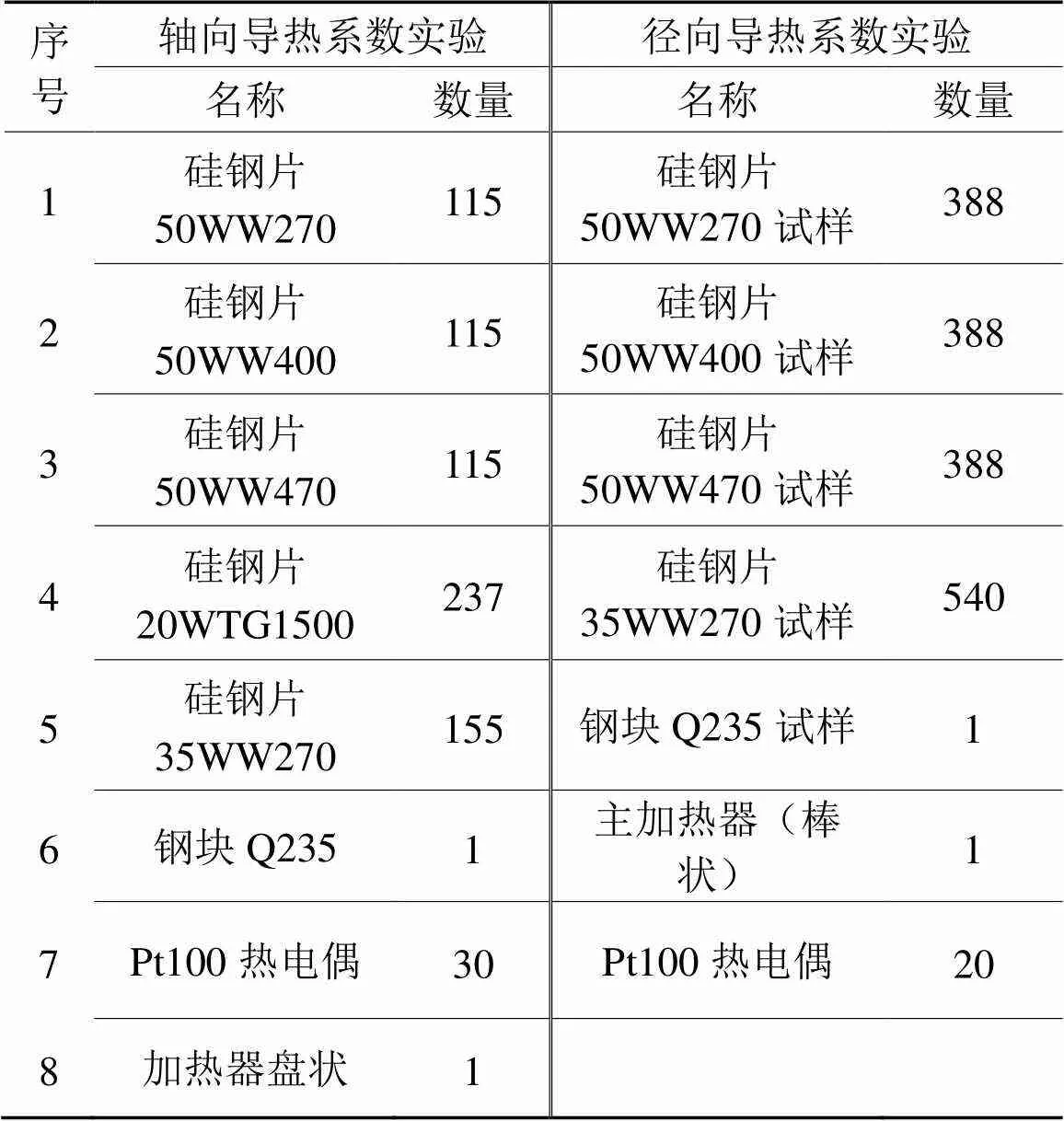
表2 导热系数实验主要装置

图3、4、5、6分别为导热系数测量实验的装置示意图。装置加工时由于各部件表面粗糙度较高，因此在实际使用时为减小接触热阻，在间隙较大处都涂抹石墨粉。

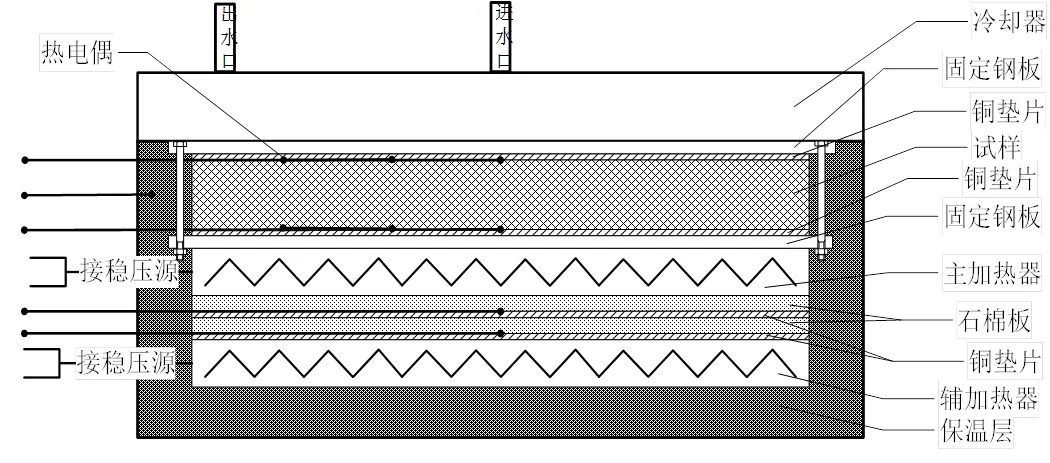
图3 轴向导热系数测试实验装置示意图

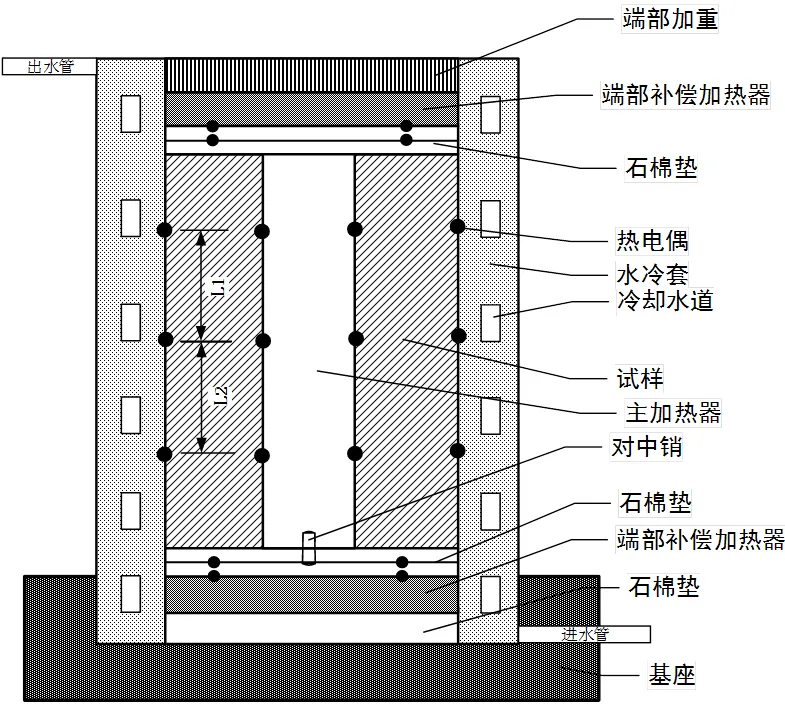
图4 径向导热系数测试实验装置示意图

利用搭建好的实验平台，对铁芯硅钢片的轴、径向导热系数展开实验测量，并对硅钢片厚度、叠压系数等不同因素对硅钢片导热系数的影响规律展开实验研究。

图5 轴向导热系数实验试样及实验系统

图6 径向导热系数实验试样及实验系统

3 实验结果分析

3.1 硅钢片导热系数随含硅量变化规律

分别测量相同叠压系数、厚度，含硅量分别为3.2%、2.6%、2.0%的三型硅钢片的导热系数。经过多次实验测量，整理实验数据可得到硅钢片轴、径导热系数随含硅量变化曲线如图7所示。

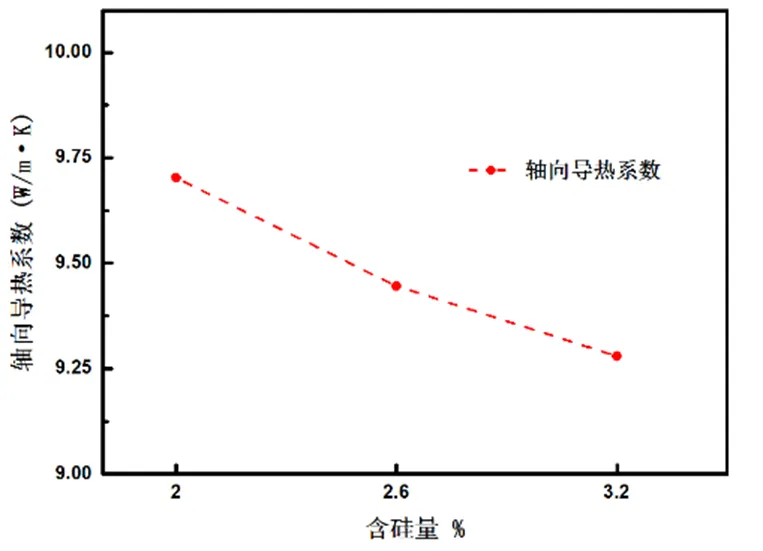
由结果可知，对于相同厚度和叠压系数的铁芯而言，其轴向与径向导热系数都随着硅钢片中硅含量的增加而减小，但是导热系数的变化程度较小，说明硅含量对硅钢片导热系数的影响较小。

3.2 硅钢片导热系数随叠压系数变化规律

分别测量具有相同含硅量、相同厚度，叠压系数分别为0.95、0.96、0.98、0.98的四型硅钢片的导热系数。经过多次实验测量，整理实验数据可得到硅钢片轴、径导热系数随叠压系数变化曲线如图8所示。

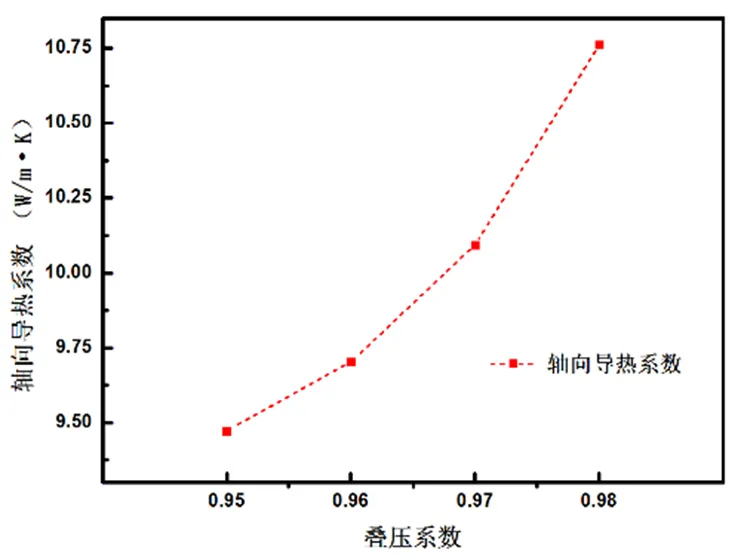
由图可知，随着叠压系数的增加硅钢片导热系数也不断增加。

3.3 硅钢片导热系数随厚度变化规律

分别测量相同叠压系数、硅含量，厚度分别为0.2、0.35、0.5 mm的三型硅钢片的导热系数。经过多次实验测量，整理实验数据可得到硅钢片轴、径导热系数随厚度变化曲线如图9所示。

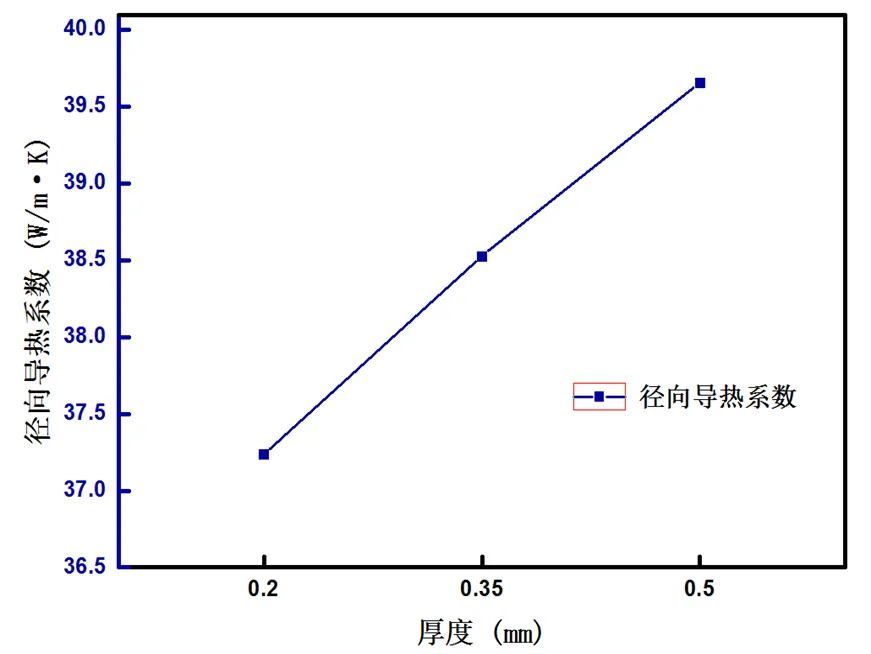
由图9可知，硅钢片导热系数随着硅钢片的厚度增加也不断增加。

4 结论

为满足新型电机设计温度场计算精度需求，本文基于传热学基本理论，采用稳态法对电机铁芯硅钢片的轴、径向导热系数以及在不同影响因素下的变化规律开展了实验研究，得出如下结论：

1）铁芯轴向与径向导热系数随着硅钢片中硅含量的减小而减小；

2）铁芯轴向与径向导热系数随着叠压系数和单层厚度的增加而变大；

3）铁芯的轴向导热系数相比于径向导热系数受叠压系数、叠压系数以及单层硅钢片厚度的影响更大；

4）设计了一种能准确测量电机铁芯轴向、径向导热系数的实验测试平台，为电机温度场的准确计算提供了支撑。

[1] 吕明杰, 岂兴明, 尹航, 江楠, 金英爱. 浅析内河纯电动船舶发展现状[J]. 船电技术, 2022, 42(01): 28-31.

[2] Rosenberry. The transient stalled temperature rise of cast-aluminum squirrel-cage rotors for induction motors[J]．American Institute of Electrical Engineers, IEEE Transactions on Power Apparatus and Systems, 1955, 74(3): 819-824.

[3] И.Ψ.菲利包夫. 电机中的热交换[M]. 北京：原子能出版社, 1980.

[4] 周秋松, 丁树业, 崔广慧. 交互式绝缘材料导热系数测定[J]. 哈尔滨理工大学学报, 2015, 20(5):31-33.

[5] 吴尧辉, 刘小梅. 小型电机绕组导热系数的研究[J]. 微电机, 2015, 48(4): 28-30.

[6] 佟文明, 孙静阳, 程雪斌. 非晶合金铁心碟片导热性系数测试与电机热分析[J]. 电工技术学报, 2017, Vol 32.

[7] 孙芝茵. 高速永磁同步电机损耗及热特性研究[D]. 哈尔滨: 哈尔滨工业大学. 2011.

[8] 王福军. 计算流体动力学分析-CFD 软件原理与应用[M]. 北京: 清华大学出版社. 2004: 1-22.

[9] 张艺耀, 龙文枫, 肖霆, 别瑜, 陈革. 基于流-固耦合的船用电源模块流场及温度场分析[J]. 船电技术, 2022, 42(02): 47-51.

[10] 万艳, 徐银飞, 付小龙, 陈娟, 文秧林. 牵引电机温升试验方法及改善措施[J]. 船电技术, 2021, 41(10): 55-58.

Measurement and influence factors of thermal conductivity of motor core

Sun Liangyou

(Xiangtan Representatives Office, Naval Wuhan Representatives Bureau, Xiangtan 411101, Hunan, China )

TM32, TM351