考虑到移相的倍频波注入方法补偿的影响分析

2022-08-12胡轩铭夏加宽

船电技术 2022年7期

关键词：径向谐波工况

胡轩铭，夏加宽

应用研究

考虑到移相的倍频波注入方法补偿的影响分析

胡轩铭，夏加宽

(沈阳工业大学电气工程学院，辽宁沈阳 110870)

为使传统不移相的谐波电流注入具有更好的力波补偿效果，采用有限元法建立了移相倍频波注入的径向力波补偿模型，并与谐波注入的补偿模型进行对比。结果表明考虑移相的倍频波注入方法相比传统的谐波电流注入对径向力波的影响更大、补偿效果更好。

表贴式永磁同步电机径向力波谐波电流注入移相倍频波力波补偿模型

0 引言

随着水下探测手段日益先进，水下航行器的隐蔽性越发需要重视。永磁同步电机作为水下航行器常用驱动设备，其低频振动占总振级很大比例，且低频振动的长波特性是影响航行器隐蔽性的重要因素。国内外采用多种结构优化方案来削弱永磁电机的振动噪声，但不能完全消除低频振动，因此需采用控制方法对低频振动进行抑制。谐波电流注入法作为抑制转矩脉动的常用方法，近年也被各国学者用来抑制电机径向振动。

文献[1]采用主动补偿5、7次谐波电流的控制策略以抑制4、6倍频径向力波。但仅讨论了4、6倍频力波各自的幅值变化，未考虑补偿电流对不同倍频力波所叠加出的总体补偿效果。文献[2]采用谐波电流注入法减小了永磁同步电机气隙中的径向激振力，改善了电机振动噪声。但仅通过减小电枢电流谐波来实现抑振，未考虑极槽结构所引起的极槽径向力波。文献[3]提出极槽效应会使永磁电机励磁磁场空间分布不完全正弦，振动不能因励磁电流中的谐波成分消除而完全消除，并注入与基波反相的谐波电流抑制极槽引起的径向振动。但反相的补偿电流不能保证产生与极槽力波反相的补偿力波，因此需要对补偿电流的初始相位进一步研究。

目前国内外多以注入各次谐波进行抑振，只讨论了谐波幅值对力波的影响，并未考虑其相位变化对力波的影响。为实现更好的补偿效果，需注入考虑到移相的倍频波进行补偿。建立移相倍频波补偿电流与径向补偿力波之间的关系模型，对移相倍频补偿来说是非常重要的。本文将聚焦低频20～1 000 Hz频段水下航行器用表贴式三相永磁同步推进电机（SPMSM）径向力波的计算，建立不同负载工况下移相倍频波补偿电流与径向补偿力波之间的关系模型。

1 谐波电流注入的径向激振力谐波

对一台3 kW水下航行器用SPMSM样机在Ansys中进行有限元仿真分析，SPMSM交直轴电感相同，d=0控制方法就是其最大转矩电流比控制方法[4]。若在Ansys中采用d=0控制，则空载时需设置转子初始位置角，使有限元模型的d轴与A相绕组轴线对齐（如图1所示），且负载时给定三相电流初始相位需设为0：

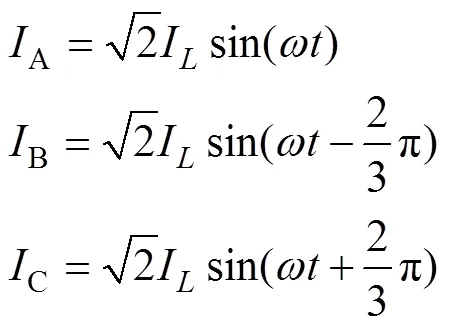
式中，IL为负载电流有效值，ω为负载电流的角频率。

谐波电流与倍频波电流不同之处在于，谐波初始相位需要与基波初始相位保持一致，向负载电流中注入次谐波电流后三相电流公式为：

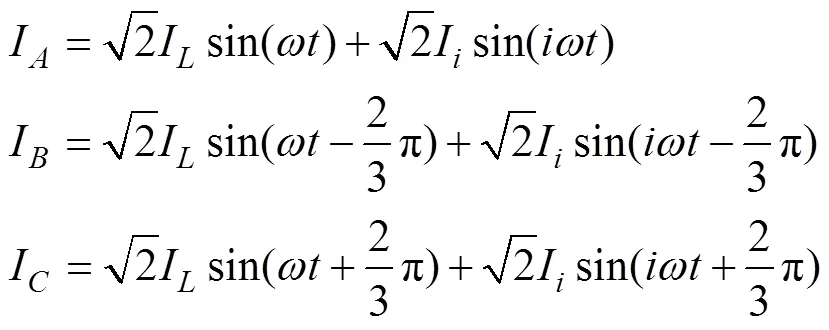
式中，I为次谐波电流有效值。

变频器供电时，谐波电流幅值约为基波电流幅值的1%～15%[5]。本文所仿真的电机额定电流有效值为10.5 A，若限制注入某一频次谐波幅值不超过额定电流10%，则该谐波有效值最高为1.05 A。以5次谐波为例，按上述额定电流的10%对其设限，则5max=1.05 A，其A相不同幅值波形如图2所示。

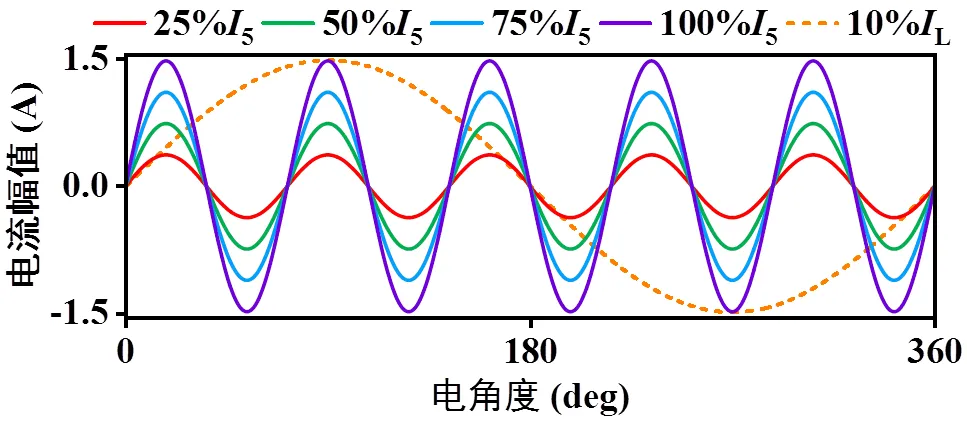
图2 注入的5次谐波电流

将图2中4种幅值的5次谐波分别注入不同的负载工况：I取值范围0～10.5 A（空载至额定负载），ΔI=2.625 A，得到如表1前三栏所示的25种试验方案，序号为1、6、11、16、21的是未注入5次谐波的对照组。通过有限元计算出这25种电枢反应下，作用在定子齿上的径向集中力波[6]时域波形（如图3所示）。

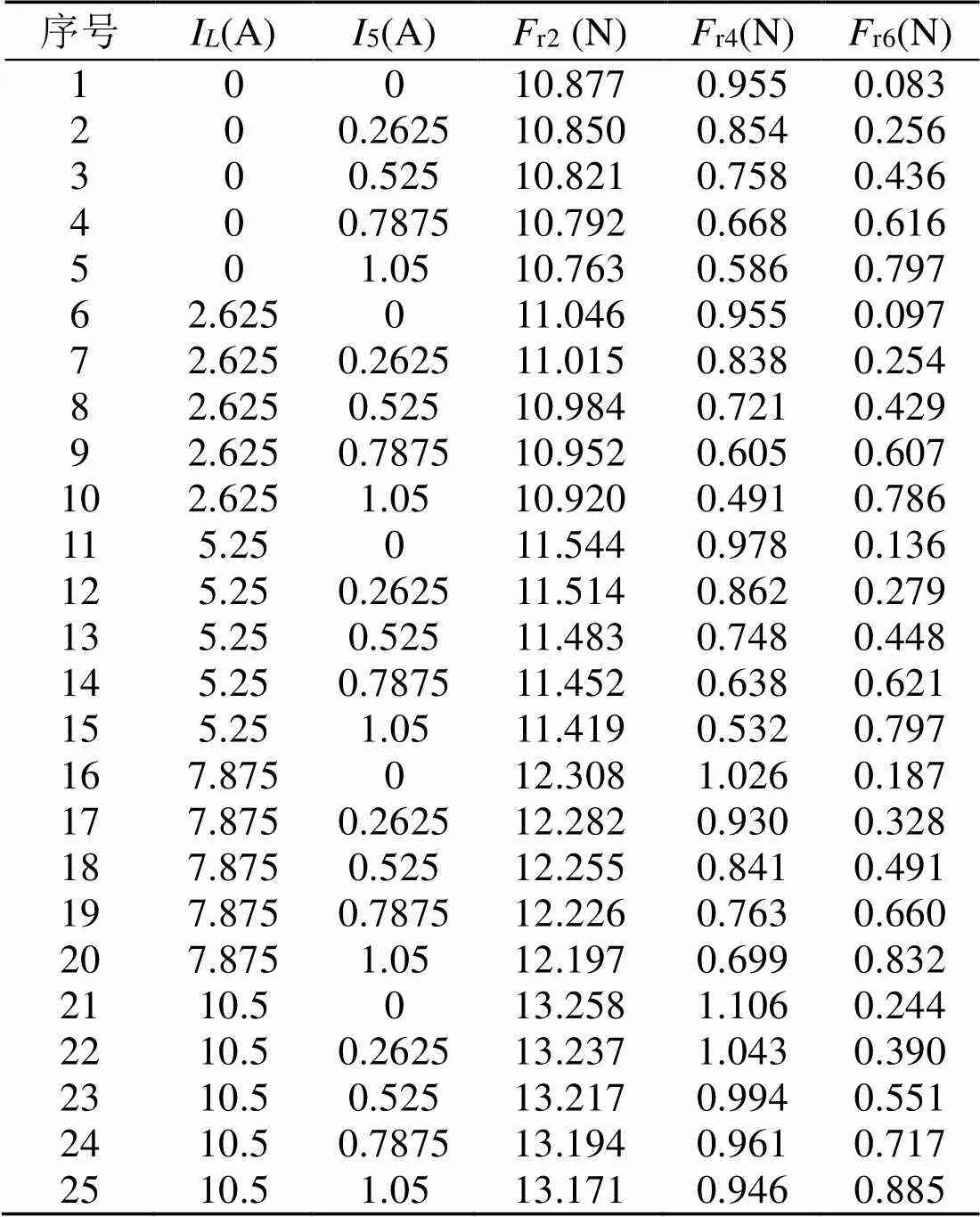
表1 注入5次谐波的径向力谐波真值表

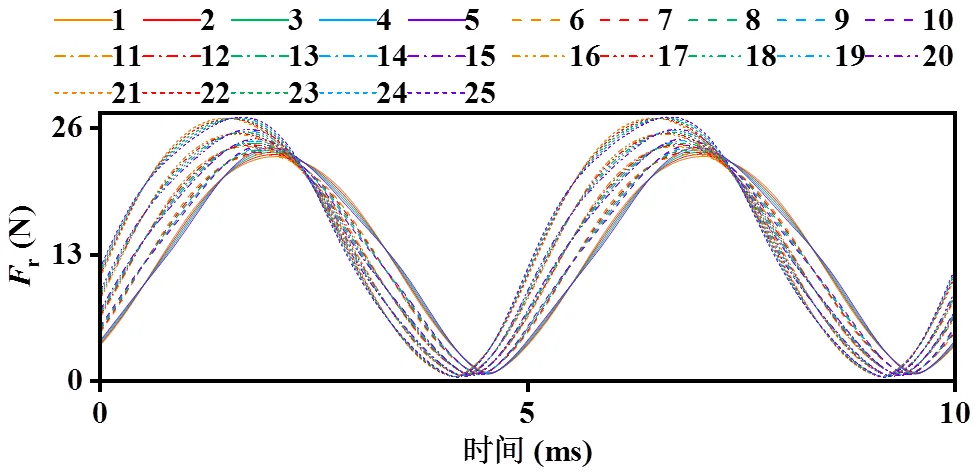
图3 注入5次谐波的径向力波时域分布

图3中图例编号与表1序号一一对应，纵坐标为径向力波有效值r，r是通过对齿上各空间位置点的径向力波幅值求均方根所得。横坐标最大值为一个电周期时间，电周期计算公式为：

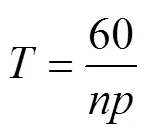
式中，为电周期时间，为转速，为极对数。

本文所仿真的推进电机极槽配合为8极48槽，则=4；仿真时设为1 500 rpm，则一个电周期时间为10 ms，基准电频率1=100 Hz。对图3中的径向力波进行快速傅里叶变换（FFT），可得不同频率下的r，将r的实际频率除以1得到力波的倍频数，表1中r2、r4、r6分别为2、4、6倍频径向力波有效值。由前人的理论分析和表1中的数据可知：5次谐波注入生成的谐波磁密与基波磁密相互作用，会产生4、6倍频径向力波[1]。因此若建立5次谐波与径向力波之间的关系模型，简化为仅对4、6倍频径向力波进行建模即可。

将表1中r4、r6数据分别进行曲面拟合，得到如图4所示的4倍频和6倍频的径向力波与注入的5次谐波之间的关系模型。图4(a)中各负载工况下的r4均随5增加而线性下降，图4(b)中的r6则均线性上升。

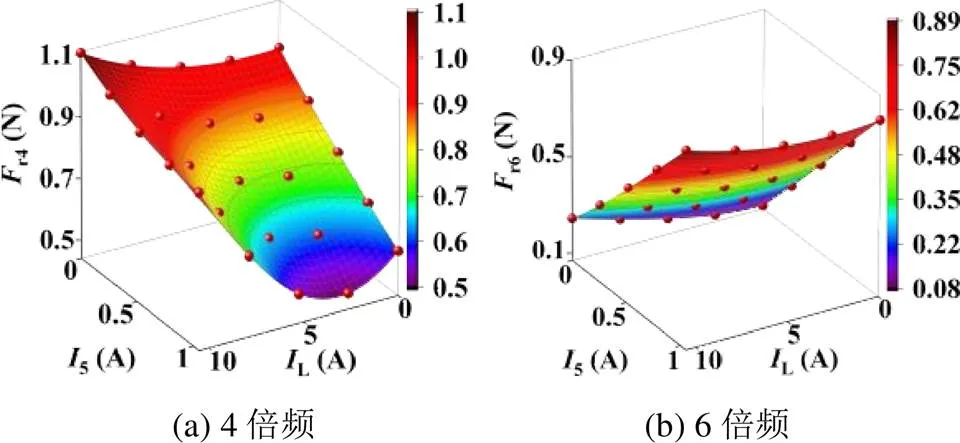
图4 注入5次谐波与径向力谐波关系模型

由图中趋势可知，5次谐波产生4倍频补偿力波的相位，与电机正弦供电时产生的4倍频极槽力波[3]相位接近于反相，因此随着5增加，补偿力波幅值也相应增加，两种力波之间的抵消作用越发强烈，使得r4迅速下降。同理，6倍频补偿力波相位则与6倍频极槽力波相位接近于同相，两种力波相互叠加使r6呈上升趋势。

2 谐波电流注入的径向力波补偿模型

分析振动常用各种振级来描述其大小，以振动加速度级为例，其公式为：

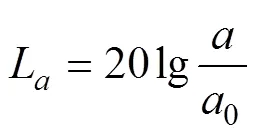
式中，L为振动加速度级，为加速度有效值，0=1×10-6m/s2为加速度基准值[7]。

由牛顿第二定律=可知力与加速度具有对应关系，因此参照式（4）近似地定义振动力波级表达式：

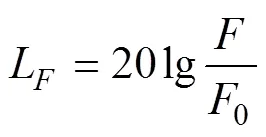
式中，L为振动力波级，为力波有效值，0=2×10-5N为力波基准值[8]。

电机振动为多个频率振动源的叠加，采用能量叠加法可将不同频率下的振动力波级合成振动力波总级[9]：

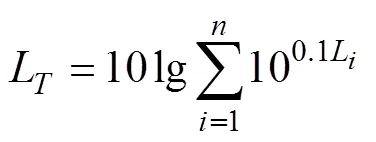
式中，L为振动力波总级，L为第个频点的振动力波级，为分析频段内参与总级计算的频点数[10]。

用未注入补偿电流的力波总级L，减去注入补偿电流后的力波总级L，可得到补偿电流所产生的力波总级L：

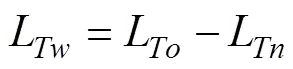
式中，L为极槽力波总级，L为激振力波总级，L为补偿力波总级。

将图3中的径向力波进行FFT后提取出20～1 000 Hz频段内的r（即r2、r4、r6、r8和r10）；将各个倍频的r分别代入式（5），得到25组2～10倍频的L；再将每组不同频率下的L代入式（6），得到25个不同电枢反应下的L；最终通过式（7）可求得20个5次谐波注入所对应的L（未注5次谐波的5个L置0）。将L数据进行曲面拟合，得到如图5所示各个工况下5次谐波补偿电流与径向补偿力波之间的关系模型，图中z轴的L越大，代表抑制极槽力波的效果越强。

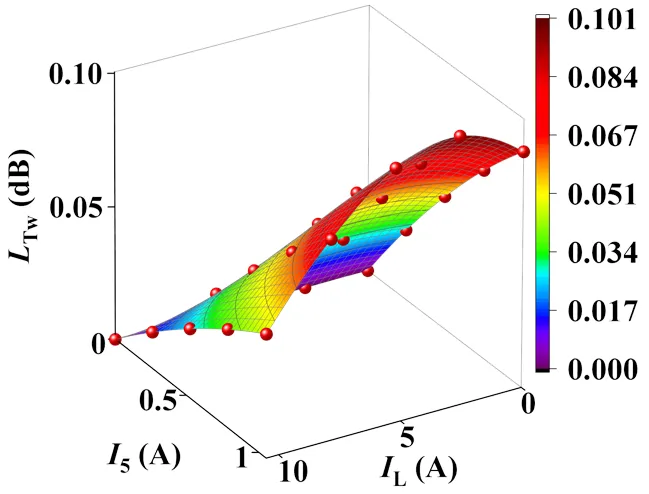
图5 注入5次谐波的径向力波补偿模型

图中各工况L随5增加而上升，但不同工况上升幅度不同：空载时补偿电流产生的径向力波补偿作用较强，最高使L下降约0.09 dB；随着负载电流增加，25%I附近的谐波补偿作用达到最强，可将该工况下的L抑制0.1 dB；之后补偿效果随负载电流的增加而迅速回落，直至额定负载工况时，L最大仅为0.046 dB。

3 移相倍频波注入的径向力波补偿模型

为达到更好的补偿效果，需要对补偿电流进行移相操作。定义与基波电流初始相位不同的次频率的电流为倍频波，即倍频波为次谐波初始相位向左或向右进行偏移后的电流。若向初始相位为0的负载电流中注入初始相位0（0≠0）的倍频波，则三相电流公式为：

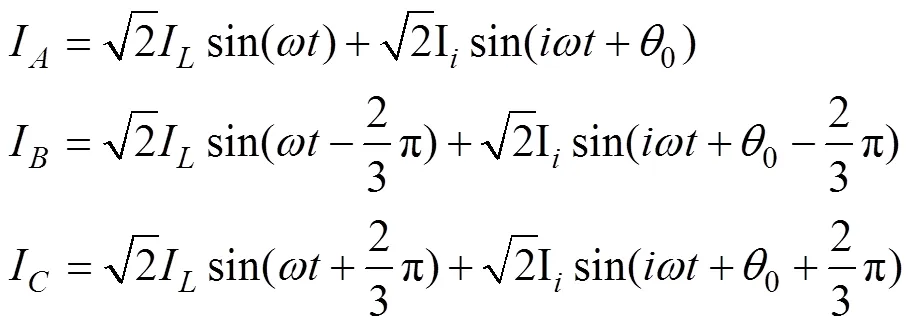
以5倍频波为例，考虑到计算量的问题，仅对5倍频波初始相位角θ5取-30°～30°这一小范围进行讨论。图6为θ5=-30°～30°（Δθ5=10°）的5倍频波一个周期的波形，其最大幅值同上文中的5次谐波一样，设为额定电流幅值的10%，其中θ5=0的波形为5次谐波，其余6个为5倍频波。

将这6种移相角度不同的5倍频波分别同前文中的5次谐波一样变幅值地注入不同工况的负载电流中，经过大量的有限元参数化计算，拟合出这6种5倍频波所对应的r4、r6关系模型。将这6组拟合模型与前文建立的5次谐波模型置于同一坐标系内，如图7所示。

图7(a)空载时5=-30°对应的r4最小，约0.5 N；随着负载电流增加，为使不同工况下r4保持最小，在2%、13%、24%、35%、46%和57%I工况附近（相邻两曲面相交处所对应的负载工况），5需增加Δ5。即2%～57%I工况内每增加11%I，图6中5倍频波需向左偏移2°。

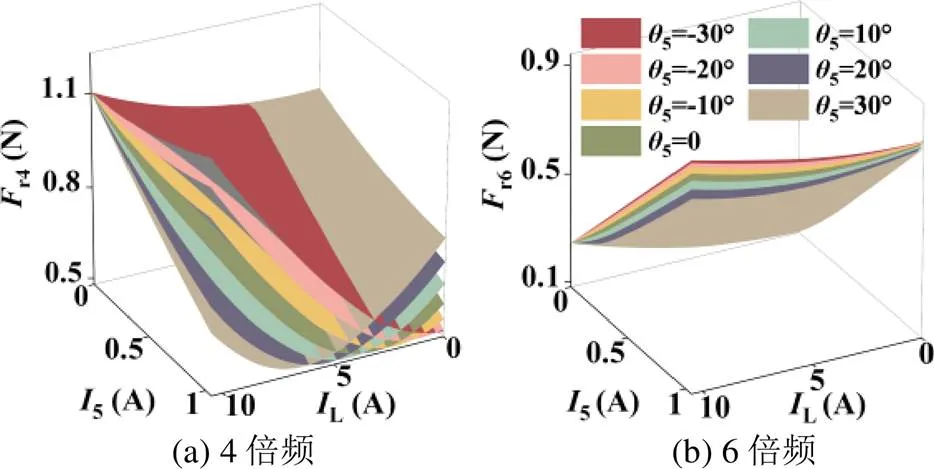
图7 注入5倍频波与径向力谐波关系模型

图7(a)中57%～100%I工况内5=30°时r4最小，但这段工况r4增幅较为明显，65%I之后r4将超过0.5 N；直至额定负载工况下，r4升至0.68 N以上。可以推断，r4在这段工况有所回升是由于5取值范围设限所致。

图7(b)中随着注入的5次谐波增加Δ5，各工况下r6的上升趋势逐渐趋缓。对比5次谐波与5倍频波注入对r4和r6的影响可知，5次谐波仅对24%～35%I工况内的r4抑制较强，而其他工况需注入移相的5倍频波才能对r4保持较强的抑制作用；而注入相对于基准谐波向右偏移的5倍频波也能对r6的上升起到一定的抑制。

为综合考虑20～1 000 Hz低频段径向激振力谐波总体被5倍频波补偿电流抑制的情况，按照图5的制作流程得到如图8所示的各个工况下注入5倍频波补偿电流的径向力波补偿模型。

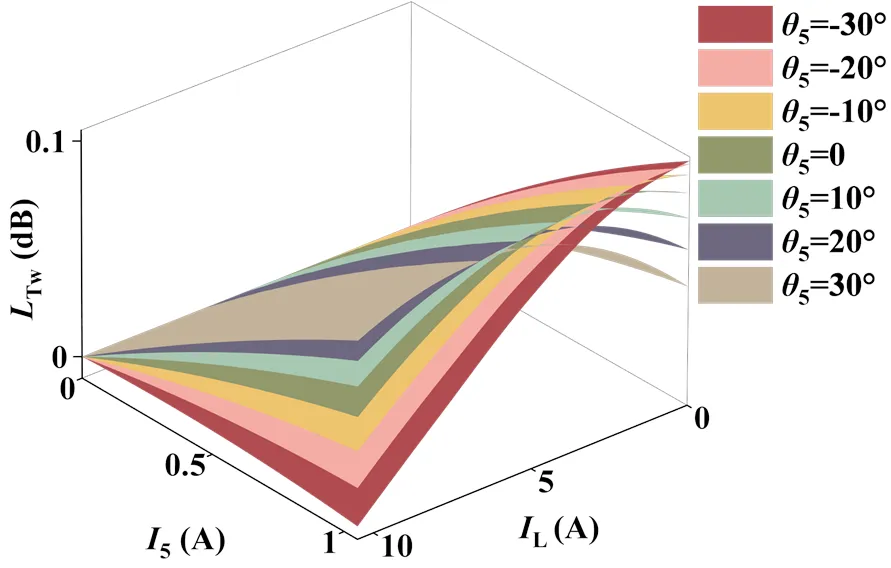
图8 注入5倍频波的径向力波补偿模型

图8中空载时，5=-30°的5倍频波产生的径向补偿力波对径向极槽力波抑制效果最显著，可将其降低0.1 dB以上。随着I从0增加，为使补偿效果更好，5也应如图7(a)所描述的，每遇到两相邻曲面相交时则增加Δ5。由于图8的5变换过程及所对应的工况与图7(a)类似，此处不再赘述。可以看到，图8中L最大值随I增加而逐渐降低，在约30%I之后L降至0.1 dB以下。直到额定负载工况时，补偿力波仅对极槽力波抑制约0.08 dB，该补偿效果的下降也与5的取值设限有关。

定量对比5次谐波与5倍频波对径向极槽力波的补偿效果可知，额定负载工况下二者差距最大（相差0.035 dB）。即额定运行时注入5倍频波相比注入5次谐波，L可提升约76%。若综合考虑补偿电流对各个工况下低频段总体的抑制作用，注入5次谐波平均可使各工况的L下降0.081 dB，而注入5倍频波使L下降0.096 dB，补偿效果提升约19%。因此，注入考虑移相的倍频波电流相比于注入传统不移相的谐波电流对径向极槽力波的补偿效果更好。

4 结语

本文以水下航行器用表贴式三相永磁同步电机作为研究对象，利用有限元软件进行了大量的仿真及数据处理，分别建立了不同工况下注入5次谐波和5倍频波补偿电流与径向力波之间的关系模型及补偿模型。通过分析补偿电流与径向力波之间的关系可知：不同工况下注入5次谐波皆可抑制4倍频径向极槽力波，同时也会使6倍频径向极槽力波幅值上升；而在不同工况下注入适当初始相位的5倍频波，会使4倍频径向极槽力波幅值下降得更多，也可使6倍频径向极槽力波幅值上升得更少。又通过定量对比注入5次谐波和5倍频波的径向力波补偿模型可知：注入5次谐波可使各个工况下20～1 000 Hz频段内的径向极槽力波平均下降0.081 dB，而注入适当初始相位的5倍频波则可使其平均下降0.096 dB。通过上述分析可得结论：注入适当初始相位的倍频波电流相比于注入传统不移相的谐波电流对于径向极槽力波的影响更大、补偿效果更好。

[1] 于浩. 永磁同步电机振动噪声抑制的主动补偿控制策略研究[D]. 沈阳: 沈阳工业大学, 2016.

[2] Martin Harries, Marius Hensgens, Rik W. De Doncker. Noise Reduction Via Harmonic Current Injection for Concentrated-Winding Permanent Magnet Synchronous Machines[C]. 2018 21st International Conference on Electrical Machines and Systems (ICEMS), 2018, pp. 1157-1162.

[3] 夏加宽, 康乐, 詹宇声, 等. 表贴式三相永磁同步电机极槽径向力波补偿模型及参数辨识[J]. 电工技术学报, 2021, 36(08): 1596-1606.

[4] 吕鹏程. 永磁同步电机参数辨识与转矩控制研究[D]. 南京: 南京邮电大学, 2020.

[5] 周吉威. 谐波电流对永磁电机振动噪声影响研究[D]. 沈阳: 沈阳工业大学, 2015.

[6] 洪剑锋, 王善铭, 孙旭东, 等. 矢量控制下的车用永磁电机电磁振动特性分析[J]. 电机与控制学报, 2021, 25(06): 1-9.

[7] 赵晗竹, 隋杰英, 李耀. 基于ANSYS的地铁列车运行对周围环境的振动分析[J]. 青岛理工大学学报, 2019, 40(03): 50-56.

[8] 彭伟才, 刘彦, 帅长庚, 等. 机械设备振源三向激励力测试方法[J]. 中国舰船研究, 2016, (03): 79-82.

[9] 刘江涛. 船舶板架结构低噪声优化设计[D]. 哈尔滨: 哈尔滨工程大学, 2019.

[10] 刘监波, 吴崇健, 陈乐佳, 等. 基于模态滤波的板壳类结构空间均方振速估算方法[J]. 中国舰船研究, 2014, 9(02): 48-54.

Influence analysis of compensation of multiple frequency wave injection method considering phase shifting

Hu Xuanming, Xia Jiakuan

(College of Electrical Engineering Shenyang University of Technology, Shenyang 110870, China)

TM351