基于多元自适应回归样条的交织区合流交互作用研究

2022-08-12李根翟伟邬岚汤祥

东南大学学报（自然科学版） 2022年4期

李根翟伟邬岚汤祥

(南京林业大学汽车与交通工程学院，南京 210037)

车辆合流辅助功能作为驾驶辅助系统的重要组成部分，可以为驾驶员提供安全的合流决策，降低潜在碰撞风险.以往的研究大多将合流过程简化成两步或三步的瞬间决策，忽视了长达数秒的合流过程[1-2].在车辆合流执行的过程中，合流车辆与原车道以及目标车道上的多辆车之间会产生复杂的交互作用[3-4].忽略这一过程，可能会影响合流辅助功能以及自动驾驶系统的安全性能.因此，准确建立换道过程中车辆间的动态交互作用模型，分析汇入过程中交互车辆的纵向加减速行为，对提高微观交通流仿真模型的准确性以及车辆辅助驾驶系统的安全性能具有重要意义.

近年来，随着车联网技术的迅速发展，国内外众多学者针对合流决策行为展开了大量研究[5-8]，然而多数研究都是将车辆换道视为一个瞬时的决策行为，采用不同的交互原理对合流交互行为构建参数模型[9-11]，其精度相对较低，难以描述车辆合流过程中高度复杂的交互作用.在后续的研究中，机器学习、深度学习等非参数模型逐渐受到研究人员的重视[12-15].非参数模型能够大幅提高合流模型的精度，但模型本身的复杂程度较高，且具有黑箱特性，难以解释和应用.其中，基于视角的刺激-反应模型(visual angle stimulate response，VASR)和梯度提升决策树(gradient boosting decision tree，GBDT)被广泛应用于交织区合流交互作用的研究.虽然，VARS模型能与跟驰行为相结合，体现横向变量对汇合交互作用的影响，但作为参数模型，其预测精度相对不足，难以准确捕捉预测曲线中的微小波动.GBDT模型能通过偏效应函数对参数进行敏感性分析，由于其复杂程度较高，且不能给出显性表达式，在工程上实用性较低.

针对上述不足，本文采用多元自适应回归样条(multiple adaptive regression splines，MARS)构建合流过程中车辆交互作用模型，深入探索合流过程中不同变量对合流车辆以及周围车辆之间交互作用的影响.MARS模型不仅可以有效预测合流交互行为，还能够深入挖掘变量之间的交互效应，并得出相应的显式表达式，可为辅助驾驶技术和无人驾驶技术提供理论和应用支撑.

1 多元自适应回归样条

MARS是一种针对高维数据的回归模型，能够在回归的建模过程中找到变量的最佳转换函数和潜在交互效应，轻易处理隐藏在高维数据中的复杂数据结构.MARS综合了投影追踪法和递归分区法的优点，并引入了样条作为基函数，通过在预测变量的不同区间中使用不同的回归斜率来近似自变量与应变量之间的非线性关系.

如图1所示，MARS通过自适应地选取节点对数据进行分割并生成对应的基函数，最终通过添加基函数构建模型，其表达式为

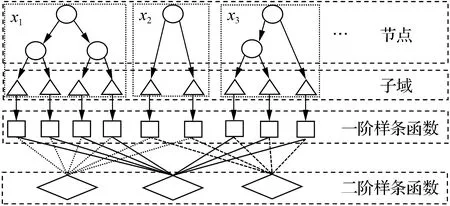
图1 MARS模型基函数原理图

(1)

式中，f(x)为目标变量的预测值；α0为截距；αi为对应第i个基函数的系数；Hi(x)为第i个基函数；N为基函数数量.基函数可表示为

(2)

式中，E为输入变量的阈值；x为预测变量.

MARS模型通过正向传递和反向传递的方式进行建模.正向传递通过自适应选取数据样本节点生成基函数，构建一个过拟合模型；反向传递则通过剪枝过程删除对模型贡献较小的基函数，在保证模型精度的前提下，提高模型泛化性能并找到最优模型.建模的过程遵循广义交叉验证原则(GCV):

(3)

式中,G为GCV值；n为输入变量的数量；t=1，2，…，M，M为样本数量；yt为目标变量的真实值;xt为影响变量的真实值；b为惩罚系数.

MARS算法的基本步骤如下：

1) 生成初始基函数(I=0)

(4)

2) 对样本t=1，2，…，M进行迭代(I≥1)，重复以下操作：

①正向传递

I=1时

(5)

I>1时

(6)

(7)

③反向传递

(8)

④更新GCV值Gnew

(9)

3) 选择最优模型

(10)

式中，yM为目标变量的最大值.

2 数据来源与变量析取

2.1 数据描述和处理

本文采用美国FHWA在NGSIM(Next Generation Simulation)项目中采集的车辆轨迹数据进行模型标定，该数据集被广泛应用于微观交通流仿真建模、驾驶行为分析等研究中.NGSIM数据集共包含4种不同道路场景的车辆轨迹数据，其中，US-101数据集具有最佳的准确性和一致性[16]，因此本文采用该数据集进行研究.如图2所示，US-101研究区域共包含5条主线车道、1条辅助车道和2条匝道，全长共640 m，主线车道使用1～5进行编号，最左侧车道为1，最右侧车道为5，辅助车道为6，进口和出口匝道分别为7和8.本文研究的范围是2个匝道之间的交织区路段.图2中，车辆M表示合流车辆，PL和PF分别表示主线车道领车和跟车，L和F表示辅助车道领车和跟车，PLL表示主线车道领车前车，PFF表示主线车道跟车后车.

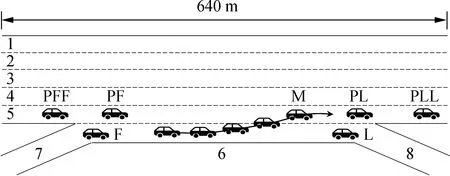
图2 US-101数据集研究区域

NGSIM提供的车辆轨迹数据包括车辆的加速度、速度、位置、车型、车头间距、车头时距等参数，时间精度为0.1 s/帧.但由于数据集本身的系统误差，车辆轨迹数据中存在错误和冗余的信息，需对US-101数据进行如下筛选处理：

1) 该数据集中车辆类型包含小汽车、摩托车、卡车，其中摩托车和卡车数据极少，筛选出摩托车和卡车的轨迹数据，并进行剔除.

2) 提取合流车辆与主线车道领跟车及其周围车辆的数据信息，剔除主线车道前后车数据缺失的车辆轨迹数据.

3) 考虑到车辆合流行为差异较大，因此剔除车头间距大于30 m或小于6 m的轨迹数据[17].

4) 该数据集中车辆的加速度是通过车辆的位移信息估计得到，存在一些随机噪声，因此数据使用前采用对称指数移动平均滤波器[17-18]对车辆的加速度和速度进行处理.

2.2 变量析取

在合流过程中，交互车辆的加速度一般会受到主线车道和辅助车道交通流的影响，交互车辆会根据与周围车辆的相对速度和相对间隙调整行驶速度.因此，影响交织区内车辆交互作用的主要因素应该包含速度差、纵向间隙和横向位置.此外，模型中引入车身碰撞时间(TTC)和车线冲突时间(TLC)2个交通安全指标，研究交通安全状态对于车辆间合流交互行为的影响.对于同向行驶的前后车，若后车车速大于前车，经过一段时间后与前车发生碰撞，这段时间差被称为TTC[19-20].在此过程中，若后车采取合流行为，由于后车车速大于前车，后车的前车身线会先通过车道线到达主线车道，极易与主线车道前车发生侧向碰撞风险，因此将后车车身线到达车道线位置的这段时间称为TLC.

如图3所示，交织区内车辆的纵向速度采用V表示，其中VPLL为主线车道领车前车的速度，VPL为主线车道领车的速度，VPF为主线车道跟车的速度，VPFF为主线车道跟车后车的速度，VM为合流车辆的速度，VL为辅助车道前车的速度，VF为辅助车道后

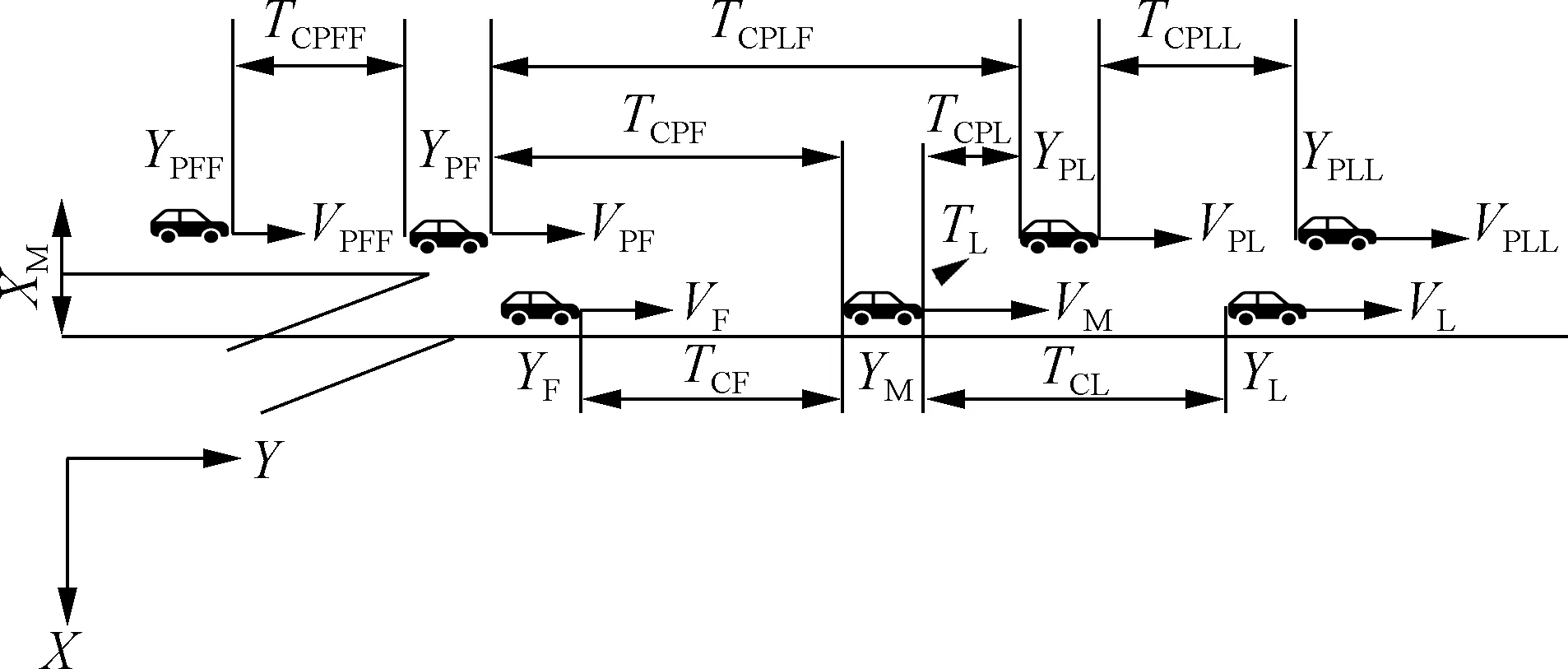
图3 影响变量示意图

车的速度；纵向间隙采用Y表示，其中YPLL为主线车道领车前车的纵向间隙，YPL为主线车道领车的纵向间隙，YPF为主线车道跟车的纵向间隙，YPFF为主线车道跟车后车的纵向间隙，YM为合流车辆的纵向间隙，YL为辅助车道前车的纵向间隙，YF为辅助车道后车的纵向间隙；XM为合流车辆的横向位置；TCPLL为主线车道领车前车与主线车道领车之间的碰撞时间；TCPLF为主线车道领车与主线车道跟车之间的碰撞时间；TCPFF为主线车道跟车与主线车道跟车后车之间的碰撞时间；TCPL为主线车道领车与合流车辆之间的碰撞时间；TCPF为主线车道跟车与合流车辆之间的碰撞时间；TCL为辅助车道前车与合流车辆之间的碰撞时间；TCF为辅助车道后车与合流车辆之间的碰撞时间.

TTC(TC)和TLC(TL)的计算公式如下：

(11)

(12)

式中，Y1和Y2分别为前车和后车的坐标，m；V1和V2分别为前车和后车的速度,m/s；L为交织区内位于前方车辆的车身长度，m；Xlane为合流车辆左车道线的横向位置，m；VMx为合流车辆的横向速度，m/s.

当合流车辆速度小于或等于领先车辆时，TTC的值为负值或无穷大.同时，当合流车辆的横向速度为负值或0时，TLC的值为负值或无穷大.这意味着合流车辆将不会与主线车道交通流发生碰撞.为研究方便，本文将TTC与TLC的取值范围设置在(0,100] s之间，即当TTC或TLC为负值或大于100 s时，其取值均为100 s.表1为本文考虑的影响变量及其含义的具体解释，其中LPLL为主线车道领车前车的车身长度；LPL为主线车道领车的车身长度；LPF为主线车道跟车的车身长度；LM为合流车辆的车身长度；LL为辅助车道前车的车身长度.

表1 影响变量选取及其含义解释

为进一步探究影响变量与目标变量之间的相关程度，对选取的所有影响变量进行Person相关系数分析.如表2所示，大部分影响变量都与其加速度存在显著的相关性.其中，变量x14与目标领车加速度的相关性以及变量x7与目标跟车加速度的相关性不显著，这主要是由于这2个变量反映的是目标领跟车与其自身后车之间的交互影响，目标领跟车在跟车过程中本身就对自身后车的影响极小；变量x15与目标跟车加速度的相关性也不显著，这说明合流车辆在采取合流措施时，目标跟车可观察到合流车辆的运动状态，对其影响较小.从表2可发现，大部分自变量和因变量之间的相关系数绝对值小于0.3，说明它们之间的线性关系较弱，采用常规的参数模型可能难以描述变量之间的复杂关系.

表2 合流交互作用影响变量相关性分析

3 交织区合流交互作用模型

3.1 MARS模型参数确定

本文利用美国Salford公司开发的数据挖掘软件Salford Predictive Modeler(SPM)以及US-101数据集中的车辆轨迹数据建立MARS模型.该模型由基函数数目N、交互程度k、节点数目J、惩罚系数b以及附加变量惩罚d五个参数决定.根据文献[21-22]，基函数数目一般设置为影响因子数目的2～4倍，为选取最佳基函数数目，本文测试了不同基函数数目下的模型精度.交互程度设置为1时，代表无交互；设置为大于等于2时，才会产生交互；当交互程度较高时，模型的复杂程度和可解读性会降低.为便于模型解读，本文将k设为2.节点数目一般是用来降低MARS模型的局部适应性，取值在10～20之间；惩罚系数设置为3；为降低模型预测变量之间的共线性，MARS在训练过程中对增加新的因变量设置了惩罚系数，通过惩罚系数鼓励在现有变量中增加节点而不是增加新的因变量，惩罚系数的设置会影响MARS模型正向传递的速度，在此设置为0.001.为了确定基函数数目，选择平均绝对偏差(MAD)、均方误差(MSE) 和GCV作为评价指标，表3列出了交互程度k=2情况下评价指标随基函数数目的变化情况.

表3 评价指标随基函数数目的变化情况(k=2)

如表3所示，合流车辆的拟合优度高于主线车道领车和跟车，表明在换道过程中，主线车道领跟车的驾驶行为更加复杂多变，难以预测，易导致交通事故.在辅助驾驶以及自动驾驶系统的设计中，主线车道领车和跟车对换道行为的反应是影响驾驶安全的关键因素之一.同时，MARS模型对不同车辆加速度的拟合效果会随着基函数数目的变化而变化，当MAD、MSE和GCV最低时，拟合效果最佳.因此，确定合流车辆M、主线车道领车PL和主线车道跟车PF的基函数数目分别为30、30和32，采用同样的方法确定各模型的节点数目，最终确定的MARS模型参数如表4所示.

表4 MARS模型参数标定

3.2 MARS模型表达式

MARS模型中生成的基函数可能会涉及多个影响变量，这些变量对合流加速度具有较为复杂的作用.如图1所示，基函数在节点处将影响变量划分成不同的区间，这意味着不同变量对交互加速度有不同的影响.

基函数H11表达式中的max(x13,one.)显示了MARS模型处理缺失数据的独有方法.MARS通过为缺失数据的变量创建基函数来处理数据，当选择的影响变量缺失数据时，该基函数的值为1(即表达式中的one.)，否则为0.以合流车辆为例，上述基函数表达式中存在max(x13,one.)，表示当变量x13为缺失数据时，该基函数取值为1.

3.2.1 合流车辆M交互作用

合流车辆M每个基函数对应的表达式如下：

H1=max(0,x2-8.232)

H2=max(0,8.232-x2)

H3=max(0,x6-63.226)

H4=max(0,63.226-x6)

H6=max(0,0.268-x15)

H7=max(0,x2-11.118)H3

H8=max(0,11.118-x2)H3

H9=max(0,x6-1.804)H2

H10=max(0,1.804-x6)H2

H11=max(x13,one.)H3

H13=max(0,x13-58.560)H11

H14=max(0,58.560-x13)H11

H15=max(0,x6-28.536)H2

H16=max(0,28.536-x6)H2

H17=max(0,x7-29.022)

H19=max(0,x1-16.855)H17

H20=max(0,16.855-x1)H17

H21=max(0,x1-20.546)

H23=max(0,x2-4.421)H22

H24=max(0,4.421-x2)H22

H26=max(0,3.513-x7)H21

H27=max(0,x10-17.879)H18

H28=max(0,17.879-x10)H18

H29=max(0,x1-19.204)H18

H30=max(0,19.204-x1)H18

H7和H8是2个较为复杂的基函数，以H7和H8为例分析变量与汇合车辆加速度之间的复杂关系，其中变量x2的节点值为11.118，并分别在节点位置与基函数H3进行交互形成基函数H7和H8，而基函数H3中变量x6的节点值为63.226，H7的系数为正，H8的系数为负，说明变量x2与变量x6存在潜在的交互效应，这种交互效应由基函数H7和H8体现.为直观展示合流影响变量之间的交互作用，选取合流加速度的MARS基函数H7和H8进行可视化处理，如图4所示.

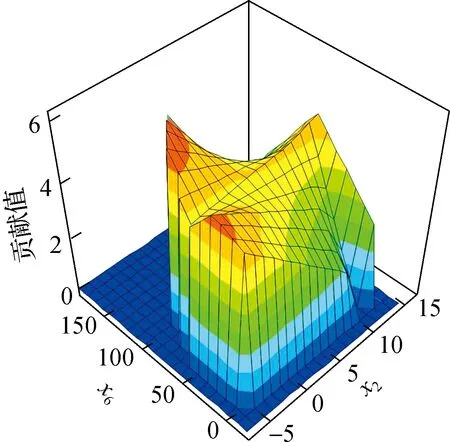
图4 合流影响变量交互作用可视化

估计得到的基函数H7和H8系数为0.079和0.014，将H7和H8中均涉及的交互基函数H3代入得到下式：

0.079H7=0.079max(0,x2-11.118)·
max(0,x6-63.226)

(13)

0.014H8=0.014max(0,11.118-x2)·
max(0,x6-63.226)

(14)

式(13)和(14)表示当合流车辆与主线车道前车的速度差大于11.118 m/s或者距离差大于63.226 m时，合流加速度值可能会增加，在此情况下，如果采取合流措施，安全性会提高.因此，最终获得的合流加速度MARS模型表达式如下：

fM(x)=0.903+0.102H1-0.300H2-

0.043H3-0.089H4-2.683H6+

0.079H7+0.014H8-0.002H9+

0.016H10-0.066H11+0.002H13+

0.002H14+0.008H15-0.012H16+

0.033H17-0.018H19-0.003H20+

1.340H21-0.029H23+0.006H24+

0.271H26-0.003H27+0.038H28-

0.027H29-0.001H30

(15)

3.2.2 主线领车PL交互作用

主线车道领车PL每个基函数对应的表达式如下：

H1=max(x11,one.)

H3=max(0,x11-19.780)H1

H4=max(0,19.780-x11)H1

H5=max(0,x15-0.353)H3

H6=max(0,0.353-x15)H3

H9=max(x2,one.)H3

H11=max(0,x2+3.780)H9

H12=max(0,-3.780-x2)H9

H13=max(0,x15-0.330)H4

H15=max(0,x10-18.135)H4

H17=max(0,x10-18.422)H4

H21=max(0,x15-0.681)H3

H23=max(0,x15-0.415)H3

H25=max(0,x15-0.338)H3

H29=max(0,x1-1.266)H1

以基函数H15为例，分析变量与主线车道领车加速度之间的复杂关系.H15中变量x10的节点值为18.135，变量x10和基函数H4构成H15，而H4是由变量x11和H1构成，其中变量x11的节点值为19.780.为了展示领车影响变量x10和x11之间的交互效应，选取领车加速度的MARS基函数H15进行可视化处理，如图5所示.

图5 领车影响变量交互作用可视化

估计得到的基函数H15系数为-0.201，将基函数H15中发生交互作用的基函数H4及基函数H4中发生交互作用的基函数H1代入得到下式：

-0.201H15=-0.201max(0,x10-18.135)·

max(0,19.780-x11)max(x11,one.)

(16)

式中，H15的系数为负值，表示当合流车辆横向位置的坐标逐渐减小时，主线车道领车的加速度将会增加，这是由于在合流过程中主线车道领车会关注合流车辆的运行状态，当合流车辆靠近时，主线车道领车将通过加速与其保持安全距离；同时，当主线车道领车与自身前车的碰撞时间小于19.780 s时，碰撞时间越小，主线车道领车的加速度值越大.最终获得的领车加速度MARS模型表达式如下：

fPL(x)=0.363-0.629H1+0.014H3-

0.732H5-0.025H6-0.002H11-

0.003H12+0.083H13-0.201H15+

0.214H17-0.079H21+0.282H23+

0.513H25+0.018H29

(17)

3.2.3 主线车道跟车PF交互作用

主线车道跟车PF每个基函数对应的表达式如下：

H1=max(0,x2+2.347)

H3=max(0,x6-75.133)H1

H4=max(0,75.133-x6)H1

H5=max(0,x4+5.342)

H7=max(0,x1-3.484)

H8=max(0,3.484-x1)

H10=max(-9.196-x4)H7

H11=max(0,x10-18.998)H1

H12=max(0,18.998-x10)H1

H13=max(0,x10-20.184)H5

H14=max(0,20.184-x10)H5

H15=max(0,x15-0.153)H1

H17=(x3,one.)

H19=max(0,x3+5.587)H17

H22=max(0,19.365-x10)

H23=max(0,x15-0.141)H21

H24=max(0,0.141-x15)H21

H25=max(0,x2+1.219)H21

H26=max(0,-1.219-x2)H21

H29=max(0,x15-0.529)H28

H30=max(0,0.529-x15)H28

H31=max(0,x2-3.194)H28

以H23和H25为例分析变量与主线车道跟车加速度的复杂关系.变量x15的节点值为0.141，变量x2的节点值为1.219，这2个基函数还和另一个基函数H21相互作用，其中变量x10的节点值为19.365.为展示跟车影响变量之间的交互效应，选取跟车加速度的MARS基函数H23和H25进行可视化处理，如图6所示.

(a) 基函数H23

估计得到的H23和H25系数分别为1.968和-0.328，为分析跟车影响变量之间的交互作用，将H23和H25中发生交互作用的基函数H21代入得到下式：

1.968H23=1.968max(0,x15-0.141)·
max(0,x10-19.365)

(18)

-0.328H25=-0.328max(0,x2+1.219)·
max(0,x10-19.365)

(19)

式(18)表明，当合流车辆与左侧车道线的碰撞时间在0.141 s以内时，主线车道跟车才会采取减速措施避让汇合车辆.这表明主线车道跟车与汇合车辆之间具有较为复杂的博弈关系.而式(19)表明主线车道跟车的加速度不仅受汇合车辆影响，还与主线车道领车存在复杂的交互作用.最终获得跟车加速度MARS模型表达式如下：

fPF(x)=1.538-0.035H1-0.003H3-0.003H4-

0.120H5-0.021H7+0.218H8+

0.065H10+0.131H11+0.125H12+

0.484H13+0.023H14-0.508H15-

0.718H17+0.031H19-0.319H22+

1.968H23-210.792H24-0.328H25-

0.245H26+67.398H29-0.189H30-

1.088H31

(20)

3.3 MARS模型结果分析

MARS模型可以通过方差分析对基函数的敏感性进行分析，其基本原理是将某一基函数组从模型中移除，并利用剩余的基函数组通过最小二乘回归构建新的MARS模型，分析其导致的标准差和GCV值损失程度.图7给出了合流车辆以及主线车道领跟车的基函数组方差，横坐标代表同一变量构建的基函数组成的基函数组，纵坐标代表所有模型的标准差和性能损失.

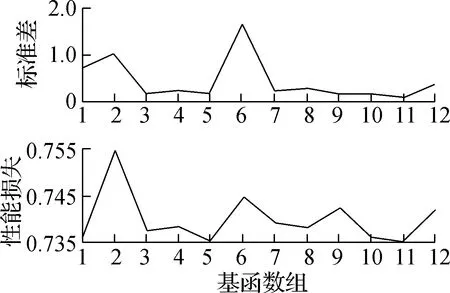
(a) 合流车辆M加速度

如图7所示，基函数组的性能损失随着标准差的变化而变化.以合流加速度的基函数组(见图7(a) )为例，可以发现，基函数组2的标准差为1.0，性能损失高达0.755，其中共包含2个基函数，这2个基函数是由变量x2和x6所创建的，说明变量x2和x6对模型的重要程度相对较高.通过分析基函数组对模型的性能损失来评估影响变量的相对重要性，并给出影响变量相对重要性排序，结果如表5所示.

从表5可以发现，缺失数据的基函数和数据中其他变量之间的交互作用在预测目标变量时是存在一定重要性的，以变量x13_mis为例，其影响程度为19.69%，说明合流车辆与辅助车道前车的碰撞时间对合流加速度的预测会受到变量缺失值的影响.由于缺失数据的基函数会和其他变量发生交互，因此MARS模型会将其他变量作为缺失变量的替代值进行预测.同时，引入的安全影响因素TTC和TLC对交互过程的加速度具有一定的影响，表明合流过程中交互车辆会将碰撞风险作为调整加速度的重要依据，未列出的影响变量被认为在模型中对汇合交互作用没有影响.和已有研究一致[13]，合流车辆M主要受到主线车道领车PL速度差的影响，其次是距离差；但主线车道领跟车的影响变量存在明显差异.主线车道领车PL主要受到前车安全因素以及后方合流车辆M的影响；而主线车道跟车PF也会受到主线车道领车PL速度差以及前方合流车辆M的影响，表明主线车道跟车主要考虑车辆前方交通流状态，忽视后方车辆的行驶状态.同时，TLC对合流车辆以及主线车道领跟车的影响相对较高，尤其是主线车道领跟车，重要性排名分别是第4和第3，这是由于合流车辆在驶入主线车道时会对主线车道车辆的正常行驶产生干扰，说明合流车辆的合流决策行为对主线车道车辆的正常运行产生很大的影响.为了进一步验证模型的准确性，利用相同的数据集分别对合流车辆以及主线车道领跟车建立VASR和GBDT模型，不同模型的MAD如表6所示.

由表6可知， GBDT和MARS模型的精度远高于VASR模型，而MARS模型的精度要略低于GB-DT模型.然而，考虑到MARS模型只需要几十个基函数即可对交互作用实现较为精确的预测，模型复杂程度远远低于GBDT模型，同时MARS模型能够提供显性表达式，这既有利于在辅助驾驶系统和无人驾驶系统中的应用，也可以帮助交通工程师与研究人员深入理解换道行为中不同的交互规则.为展现不同模型对于合流交互动态加速度的预测结果，随机选择编号为2990的合流车辆与其主线车道领跟车结果进行测试和比较.如图8所示，可以发现，MARS和GBDT模型对动态加速度aM、aPL和aPF的预测值与实际值非常接近，且具有较高的预测精度.观察不同模型的预测曲线变化发现，GBDT模型的预测精度虽然较高，但其预测曲线中会存在微小的波动，这些微小波动在提高模型预测精度的同时，也大大增加了模型的复杂程度.在无人驾驶或辅助驾驶系统中，较多的曲线波动不仅容易增加系统的计算负荷，也会降低驾乘人员舒适度，而MARS模型却能够很好地捕捉动态加速度的曲线趋势，加速度曲线比较平滑.

表6 模型预测精度比较

(a) 合流车辆

3.4 交互程度分析

为分析交互程度对模型预测结果的影响，本文对不同交互程度的模型预测结果进行分析，结果如表7所示.

表7 不同交互程度下的MARS模型预测精度

可以发现，不同的交互程度对MARS模型预测精度存在一定影响.其中，合流车辆的最佳交互程度为2，随着交互程度的增加，主线车道领跟车的MAD、MSE和GCV有所降低，但幅度较小.考虑到模型复杂程度的增加，本文针对合流交互行为采用交互程度为2的MARS模型是合理的，既能够突出影响变量之间的交互作用，又能够降低模型的复杂程度.