一个高效的安全两方近似模式匹配协议

徐 琳 魏晓超 蔡国鹏 王 皓 郑志华

(山东师范大学信息科学与工程学院 济南 250358)

模式匹配作为计算科学领域中的一个典型问题，其功能是确定模式在文本中出现的位置.近似模式匹配(approximate pattern matching, APM)作为最适合实际应用的模式匹配变体，常用于人脸识别、基因匹配、文本处理、数据挖掘和计算生物学等领域.如在人脸识别中，当光线、表情或位置不同时，我们提取的人脸图像的特征数据也不同.因此，在与数据库中存储的特征模板进行匹配时，需要根据相似程度来判断人脸的身份信息，而不是根据它们是否相同.

在安全两方计算[1-2]中，互不信任的2个参与方希望共同计算关于他们隐私输入的某些函数，而不会泄露除了函数输出以外的其他任何信息，同时确保某些安全属性，例如隐私性、正确性等.随着人们隐私保护意识的不断增强，安全模式匹配作为安全两方计算中领域的一个典型问题，成为当下的重要研究内容.

现在考虑场景：某基因研究中心拥有一个RNA病毒库，某研究人员持有一个未知病毒的RNA序列.研究人员希望确定病毒库中是否存在与未知病毒相似的RNA序列，因为相似的2个RNA序列会存在部分相似的特征.然而，研究人员不愿向研究中心透露其正在研究的未知病毒的序列，而研究中心也不希望向研究人员透露其他无关RNA序列的信息.显而易见，安全近似模式匹配可以很好地解决该场景中的问题.因此，安全近似匹配是至关重要且实用的，它既能实现近似匹配功能，又能保护双方隐私信息的安全性.

本文主要考虑安全近似模式匹配场景：数据库方持有长度为n的文本字符串t∈{0,1}n，用户持有长度为m的模式字符串p∈{0,1}m，同时双方共享某阈值τ.用户希望仅自己知道与其模式相匹配的文本子串的位置(模式p与文本子串之间的汉明距离小于τ，即为匹配成功)，同时数据库方不会获得关于用户模式的任何信息.而数据库方希望用户不会获得关于其文本的其他额外信息.本文主要考虑半诚实敌手模型下的协议，即敌手严格遵循协议的执行，但却是“好奇”的，其试图通过收到的信息以及所处的状态推测出其他额外信息.

1 相关工作和主要工作

1.1 相关工作

据我们所知，首次在安全计算环境中考虑近似模式匹配问题的工作是Troncoso-Pastoriza等人[3]，他们提出了一种基于茫然自动机的隐私保护容错DNA查询协议.该协议能够确定一方持有的描述导致疾病突变的短字符串是否存在于另一方拥有的DNA序列中.Gennaro等人[4]基于茫然自动机计算提出了安全计算近似模式匹配问题的有效协议，他们的协议首次在恶意敌手模型中实现完全模拟.

Hazay等人[5]基于Elgamal同态加密提出了恶意敌手模型下的安全近似模式匹配协议.协议双方分别将他们的输入分解为比特，并对每个比特进行加密.为了确定匹配，双方使用Elgamal加密的同态性质计算加密的汉明距离，并判断这些汉明距离是否小于阈值τ.之后Hazay等人[6]改进了协议的汉明距离计算阶段，将通信复杂度由O(nm)降低至O(nτ).然而，由于他们的协议主要使用同态加密技术，所以协议的计算复杂度一直是O(nm).

Vergnaud[7]通过采用一种新的快速傅里叶变化(fast Fourier transform, FFT)方法，研究了恶意敌手模型下的安全近似模式匹配协议.他们的协议依赖于Fischer等人[8]在1974年提出的一种著名的模式匹配技术，其中输入被视为2个多项式的系数，它们的乘积通过使用FFT计算.

Yasuda等人[9]使用Somewhat同态加密的对称密钥变体方案设计了一个安全近似模式匹配协议，但是他们没有证明协议的安全性.

Samadani等人[10]利用Shift-ADD算法[11]的特性进行安全近似模式匹配，他们的构造在单边模拟的恶意敌手模型中是安全的.最近，Zarezadeh等人[12]也基于Shift-ADD算法以及同态加密技术构造了一个在恶意敌手模型中实现完全模拟的安全近似模式匹配协议.遗憾的是，协议[10,12]在近似模式匹配过程中会泄露汉明距离.若考虑不泄露汉明距离的情况，则需在密文状态下比较汉明距离与给定阈值.

除了在标准模型下构造的工作外，还有诸多工作在云辅助模型下考虑安全近似模式匹配问题，如魏晓超等人[13]基于茫然传输扩展(oblivious transfer extension, OT extension)技术以及秘密分享构造了安全外包近似模式匹配协议，他们将重构阶段外包给诚实但好奇的云服务器，以降低参与方的计算负担.

1.2 本文的主要工作

本文基于茫然传输、同态加密以及茫然多项式计算技术构造了一个安全、高效的近似模式匹配协议，协议在半诚实敌手模型下满足安全性要求.

协议有2个参与方，分别是数据库方D以及用户U.其中，数据库方提供文本信息，用户提供模式信息.如图1的系统模型所示，协议主要分为4个阶段，分别是茫然传输阶段、汉明距离计算阶段、匹配阶段以及输出阶段.系统需要保证用户在不泄露其模式信息的前提下查询其模式在数据库方的文本中出现的位置信息.同时，系统也需要保证数据库方文本的其他信息不被泄露.

Fig. 1 System model of secure approximate pattern matching图1 安全近似模式匹配系统模型

本文的贡献主要包括3个方面.

1) 首次基于茫然传输、加法同态加密、茫然多项式计算以及隐私等值比较技术给出了一个半诚实安全的近似模式匹配协议的高效构造.协议的主要思想是：首先，通过茫然传输协议，用户在无法获得文本信息的情况下获得盲化后的文本子串比特与对应位置模式比特的异或值.其次，结合同态加密技术，可计算出盲化后的文本子串与模式之间的汉明距离.最后，利用茫然多项式计算以及隐私等值比较技术，就可以判断汉明距离是否小于τ，并最终得到正确结果.

2) 与现有的安全近似模式匹配工作相比，我们的协议在计算复杂度方面更高效，其中协议的轮复杂度为O(1)，计算复杂度为O(nτ)，通信复杂度为O(nm).

3) 为了检验协议的高效性，我们进行了性能评估.实验结果表明：当模式长度为26、文本长度为212时，协议仅需10 s运行时间.

2 基本知识和安全定义

2.1 茫然传输及其扩展协议

茫然传输(oblivious transfer, OT)是密码学中重要的基本原语之一，被广泛应用于安全计算领域.OT最早是由Rabin[14]提出的，在这种OT中，发送方向接收方发送一条消息，接收方能够以1/2的概率收到消息.在OT执行结束后，发送方不知道接收方是否收到了消息，而接收方可以确切地知道是否收到了消息.另一种比较实用的OT协议，称为1-out-of-2 OT，它是由Even等人[15]提出的.在1-out-of-2 OT协议中，发送方每次向接收方发送2个有序消息(x0,x1).接收方输入一个选择比特σ，并根据自己的输入得到输出.在协议结束时，接收方仅获得消息xσ，不会得知关于另一消息的信息，而发送方不会得知接收方最后获得的是哪一个消息.

在具体的安全多方计算协议中，需要执行的OT协议数量可能高达数百万个.因此，OT协议的效率成为影响安全多方计算协议效率的重要因素.在这种情况下，Beaver[16]借鉴混合加密的思想，首先提出了茫然传输扩展技术.OT扩展协议通过运行少量的基础OT协议，再结合廉价的伪随机替换操作，即可实现执行大量OT协议的效果.然而，遗憾的是，这种构造并不高效.之后，Ishai等人[17]提出了一种OT扩展协议，这是半诚实敌手模型中第1个高效的OT扩展协议.后续Kolesnikov等人[18]改进了Ishai等人的OT扩展方案，他们将1-out-of-2 OT扩展协议扩展为1-out-of-nOT扩展协议，同时提高了效率.Asharov等人[19]在标准模型下构建了一种新的OT协议，并将其用于OT扩展技术，降低了计算和通信的复杂性.

当前，基于OT扩展技术的协议较之于其他技术实现的协议更为高效，因而本文也将使用Ishai等人[17]的OT扩展技术来改进安全近似模式匹配协议的效率，协议描述如下：

协议1[17].

S输入：m对有序消息(xj,0,xj,1)∈{0,1}l，1≤j≤m；

R输入：m个选择比特r=(r1,r2,…,rm)；

共同输入：安全参数k；

谕言机：随机谕言机H:[m]×{0,1}k→{0,1}l；

1)S随机选择s∈{0,1}k，R准备一个m×k的随机比特矩阵T.

3)S将接收到的值形成m×k矩阵Q，其中qi=(si·r)⊕ti，qj=(rj·s)⊕tj.对于1≤j≤m，R发送(yj,0,yj,1)，其中yj,0=xj,0⊕H(j,qj)，yj,1=xj,1⊕H(j,qj⊕s).

4) 对于1≤j≤m，R输出zj=yj,rj⊕H(j,tj).

2.2 加法同态加密

在一个公钥加密方案(KeyGen,Enc,Dec)中，(pk,sk)是KeyGen(1k)的输出，和分别是明文空间和密文空间.对任意m1,m2∈和c1,c2∈，其中m1=Dsk(c1)且m2=Dsk(c2)，若有式：{pk,c1,c1×c2}≡{pk,Encpk(m1),Encpk(m1+m2)}，则我们称该公钥加密方案是加法同态加密(additive homomorphic encryption, AHE)的.

2.3 茫然多项式计算

茫然多项式计算(oblivious polynomial evaluation, OPE)最早是由Naor等人[20]提出的.OPE是一个两方协议，P0持有秘密多项式p(·)，而P1持有秘密元素x.OPE允许P1得到p(x)，但无法获得多项式p(·)，同时P0无法得知P1持有的x.OPE常应用于诸多密码学方案中，如茫然关键字查找[21]、集合求交[22]等.

本文将使用赵永骏等人[23]所提及的茫然多项式计算方案，方案描述为：在OPE协议中，一方持有1个n阶多项式p(·)，通过使用同态加密方案加密此n阶多项式p(·)的系数a0,a1,…,an以隐藏其本身，并将这些加密系数Encpk(p(·))发送给持有明文的参与方.持有明文x的参与方可基于同态性质Encpk(a0)×(Encpk(a1))x×(Encpk(a2))x2×…×(Encpk(an))xn来计算得到Encpk(p(x)).

对于协议1，就计算复杂度而言，我们主要考虑加密操作和模幂运算，因而协议1的计算复杂度为O(n).就通信复杂度而言，协议1仅存在发送加密多项式系数，因此通信复杂度为O(n).

2.4 隐私等值比较

隐私等值比较(private equality test, PEQT)允许发送方和接收方分别输入字符串x0和x1，且接收方仅获得0或1以表示x0与x1是否相等，但不会得知其他任何信息.功能函数FPEQT描述为：

功能函数FPEQT.

输入：

1) 发送方输入字符串x0∈{0,1}*；

2) 接收方输入字符串x1∈{0,1}*.

输出：

1) 如果x0=x1，接收方输出1，否则输出0；

2) 发送方无输出.

当PEQT协议首次被提出时，它依赖于复杂的公钥操作，开销很大.但Kolesnikov等人[24]的协议仅通过使用少量基础OT协议以及一些对称操作，就实现了大量PEQT协议的执行效果.本文将使用Kolesnikov等人[24]的PEQT协议，但鉴于Kolesnikov等人仅描述了协议的主要思想且给出了关键模块的构造，因此我们给出协议具体描述为：

协议2[24].

S输入：m个字符串u=(u1,u2,…,um)，其中ui∈{0,1}*;

R输入：m个字符串r=(r1,r2,…,rm)，其中ri∈{0,1}*;

其他参数：

(κ,ε)-伪随机码函数簇C，输出长度k=k(κ)；κ-汉明相关性鲁棒Hash函数H:[m]×{0,1}k→{0,1}v；

1)S选择一个随机C←C，并将其发送给R.

2)S随机选择s←{0,1}k，si表示s的第i个比特.

3)R生成m×k矩阵T0，T1：

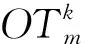
5) 对于每一个j∈[m]，S输出伪随机函数种子((C,s),(j,qj))，R输出松弛伪随机函数输出(C,j,t0,j).

6) 对于每一个j∈[m]，S通过伪随机函数种子计算其输入u=(u1,u2,…,um)的伪随机函数输出，记为t2,j=qj⊕(C(uj)·s)，并将t2,j发送给R.

7) 对于每一个j∈[m]，R简单比较t0,j与t2,j是否相等.若t0,j=t2,j，R输出1，否则输出0.

就计算复杂度而言，协议2主要通过执行k次基础OT协议，并结合一些Hash操作，实现了PEQT协议，因此协议2的计算复杂度为O(k).考虑通信复杂度，协议2实现m×k矩阵，因此通信复杂度为O(mk).

2.5 计算不可区分性

假设X={X(a,n)}a∈{0,1}*;n∈和Y={Y(a,n)}a∈{0,1}*;n∈是2个分布总体.对任意一个非均匀多项式时间算法D，如果存在一个可忽略函数negl(·)，对于每个a∈{0,1}*和每个n∈，不等式成立：

|Pr[D(X(a,n)=1)]|-
|Pr[D(Y(a,n)=1)]|≤negl(·),

则我们说这2个分布总体是计算不可区分的，表示为X≡Y.

2.6 安全性定义

本文主要考虑的安全模型是半诚实敌手下的安全两方计算模型，并基于理想/现实模拟范式[25-26]给出形式化的安全性定义.敌手严格遵循协议，但是试图通过观察其收到的信息以及其所处的状态来推测出其他额外信息.我们给出基于理想/现实模拟范式的形式化安全性定义.

定义1.令f:{0,1}*×{0,1}*→{0,1}*×{0,1}*是一个两方函数，π是一个两方现实协议.协议π在半诚实敌手的情况下安全计算f，如果对于真实模型中的每一个非均匀概率多项式时间敌手，在理想模型中就存在一个非均匀概率多项式时间模拟器，对于2个参与方的输入x和y以及i∈{1，2}满足:

{IDEALf,S(z),i(x,y,n)}x,y,z,n≡
{REALf,A(z),i(x,y,n)}x,y,z,n,

其中，x,y,z∈{0,1}*,n∈.

3 安全近似模式匹配协议

3.1 安全近似模式匹配功能函数

本文所考虑的安全近似模式匹配功能函数FAPM中主要涉及2个参与方，分别是数据库方D和用户U.其中数据库方和用户分别持有文本字符串t和模式字符串p.功能函数FAPM要求用户U能够得到其模式与数据库方的文本字符串近似匹配的位置，从而实现模式匹配功能.当文本子串与模式串之间的汉明距离小于阈值τ时，该子串与模式串即满足近似匹配.

同时，功能函数FAPM要保证3种安全属性：

1) 用户U的模式信息对数据库方是保密的.

2) 数据库方D的文本信息对用户是保密的.

3) 用户U只有在匹配成功的情况下才能获得相应的位置信息，而当匹配失败时，不能得到关于文本t的任何信息.

下面我们给出功能函数FAPM的形式化描述：

功能函数FAPM.

输入：

1) 数据库方D输入字符串t∈{0,1}n、整数m以及阈值τ；

2) 用户U输入字符串p∈{0,1}m、整数n以及阈值τ.

输出：

1) 当且仅当文本t的第i个子串与模式p之间的汉明距离小于阈值τ时，用户U输出位置i；

2) 数据库方D无输出.

3.2 安全近似模式匹配协议构造

本节我们给出了半诚实敌手模型下的安全高效的近似模式匹配协议构造.协议主要基于茫然传输、同态加密、茫然多项式计算和隐私等值比较.通过茫然传输扩展协议，用户能够在不知道文本信息的情况下，获得盲化后的模式p的每一比特与文本子串对应的每一比特的异或值.这一步的思想主要源于宋祥福等人[27]的共享等值比较协议.通过同态加密计算，数据库方可获得盲化后的ti与模式p之间的汉明距离.通过茫然多项式计算与隐私等值比较，用户可获得其模式在数据库方的文本中出现的位置.

安全近似模式匹配协议的流程大致分为4个阶段：

1) 茫然传输阶段.数据库方将其选择的随机数嵌入到茫然传输扩展协议的输入中，以达到盲化其文本的目的.通过茫然传输扩展协议，用户可以获得盲化后的模式p的每一比特与文本子串ti对应的每一比特的异或值.

2) 汉明距离计算阶段.用户对盲化后的比特异或值进行计算，得到盲化后的ti与模式p之间的汉明距离.数据库方对其选择的随机数进行求和运算，使用其公钥加密后发送给用户.用户通过加法同态加密计算得到密文状态下的汉明距离，盲化后将其发送给数据库方解密.

3) 匹配阶段.数据库方和用户通过茫然多项式计算和隐私等值比较判断文本子串ti与模式p之间的汉明距离是否小于阈值τ.如果汉明距离小于阈值τ，用户获得输出1，否则获得输出0.

4) 输出阶段.用户根据输出是否为1确定相应子串是否匹配成功，最终输出匹配位置.

在介绍协议之前，我们先介绍协议中用到的符号，如表1所示:

Table 1 Notations of Secure Approximate Pattern Matching Protocol表1 安全近似模式匹配协议符号含义

本文所构造的协议具体描述如下：

协议3.安全近似模式匹配协议πAPM.

输入：数据库方D输入字符串t∈{0,1}n、整数m以及阈值τ；用户U输入字符串p∈{0,1}m、整数n以及阈值τ；

输出：当且仅当文本子串ti与模式p之间的汉明距离小于阈值τ时，用户U输出位置i.

协议：

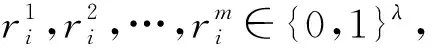
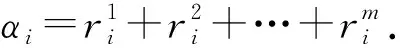
3) 数据库方D和用户U通过茫然多项式计算和隐私等值比较判断ri+Hi是否与ri,ri+1,ri+2,…,ri+τ-1中之一相等.若相等，则表明文本子串ti与模式p之间的汉明距离小于τ，即文本子串ti与模式p匹配.

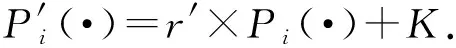
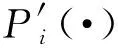
4) 用户U判定bi中哪些值为1，以此确定模式p在t中出现的位置.

① 若存在bi=1，表示文本子串ti和模式p匹配成功，则输出i;

② 否则，输出⊥，表示匹配失败.

3.3 协议正确性

安全近似模式匹配协议的正确性是指在协议运行结束之后，用户U得到正确的结果.具体而言，如果在数据库方的文本t中存在与模式p近似匹配的子串，则用户一定输出该子串的起始位置，否则用户输出⊥，匹配失败.

首先需要说明的是，通过茫然传输协议，用户能够获得正确的盲化后的比特异或值.我们就2种情况分别进行说明：

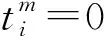
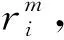
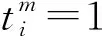
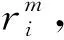
其次需要说明的是，通过茫然多项式计算和隐私等值比较，用户能够得到正确的匹配结果.我们就2种情况分别进行阐述：

综上所述，用户U在匹配成功和失败情况下均能输出正确的结果，因此协议正确性满足.

3.4 协议安全性

我们给出安全近似模式匹配协议的形式化安全证明：

定理1.假设茫然传输协议和隐私等值比较协议在半诚实敌手模型下是安全的，加密方案是CPA安全的，根据定义1，协议πAPM在半诚实敌手模型下能够安全计算功能函数FAPM.

证明. 我们在(FOTE,FPEQT)-混合模型中证明协议πAPM的安全性，其中FOTE与FPEQT是理想功能函数.我们分别对数据库方D和用户U被腐化2种情况进行证明.

1) 数据库方D被腐化

数据库方D的视图：

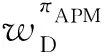
假设数据库方D被多项式时间敌手A腐化.我们构建一个多项式时间模拟器SD，SD调用敌手的输入输出且扮演诚实方U的角色与敌手交互.模拟器的行为：

①SD模拟理想功能函数FOTE的执行.

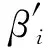
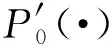
⑤SD模拟理想功能函数FPEQT的执行.

我们可以得到模拟器SD的输出：

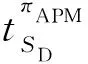
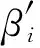
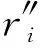
2) 用户U被腐化

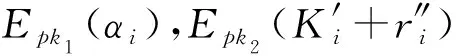
用户U的视图：

假设用户U被多项时间敌手A腐化.我们构造一个多项式时间模拟器SU，SU调用敌手的输入输出并且扮演诚实方D的角色与敌手交互.模拟器SU的行为：

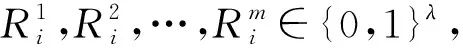
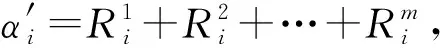
④SU模拟理想功能函数FPEQT的执行，并将bi∈{0,1}发送给敌手A，其中协议输出位置i对应的bi为1，其余为0.

我们可以得到模拟器SU的输出：

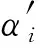
综上所述，我们完成对定理1的证明.

证毕.

3.5 协议效率分析与比较

我们将就轮复杂度、计算复杂度和通信复杂度3方面对协议进行效率分析，并给出与相关工作的效率比较.

1) 轮复杂度.我们所构造的安全近似模式匹配协议共需要9轮交互.其中，在茫然传输扩展协议中，需要进行2轮交互.此外，在汉明距离计算阶段和匹配阶段中，共需要4轮交互.注意，用户U可以在1轮交互中将盲化后的汉明距离的密文以及多项式系数的密文发送给数据库方D.最后，在输出阶段中，隐私等值比较协议需要3轮交互.

2) 计算复杂度.协议的计算复杂度主要涉及到对称操作和非对称操作.其中，对称操作速度快、代价小，如Hash、异或等.而非对称操作速度慢、代价大，如加密、解密、模幂运算等.因此，我们主要考虑通过非对称操作的数量来衡量协议的计算复杂度.在安全近似模式匹配协议中，我们调用了1次茫然传输扩展协议、n-m+1次茫然多项式计算协议、1次隐私等值比较协议.在2.1节中，可知茫然传输扩展部分的计算复杂度为O(k)，其中k为基础OT协议的数量且k≪nm.在2.3节中，可知茫然多项式计算协议的计算复杂度与多项式的阶数有关.而本协议中多项式的阶数为τ，所以茫然多项式计算部分的计算复杂度为O((n-m)τ).在2.4节中，可知隐私等值比较部分的计算复杂度也为O(k)，k为基础OT的数量且k≪nm.另外，在协议3的步骤2)中，所执行的加密操作与解密操作的数量分别为3(n-m+1)和n-m+1.在协议3的步骤3)中茫然多项式计算结束后，所执行的加密操作与解密操作的数量分别为n-m+1和n-m+1.相对于茫然多项式部分的计算复杂度来说，OT扩展协议和PEQT协议的计算复杂度是可忽略的.因此，安全近似模式匹配协议的计算复杂度为O((n-m)τ).考虑到实际情况中m的大小相对于n是可忽略的，所以我们协议的计算复杂度为O(nτ).

3) 通信复杂度.通信复杂度是指参与方之间发送和接收的信息数.首先，在安全近似模式匹配协议中，执行1次OT扩展协议需实现(n-m+1)×m矩阵效果，执行1次隐私等值比较协议也需实现(n-m+1)×m矩阵效果，所以OT扩展与隐私等值比较部分的通信复杂度都为O(nm).在2.3节中，可知茫然多项式计算协议的通信复杂度与多项式的阶数有关.而本协议中调用n-m+1次茫然多项式计算协议，且多项式的阶数为τ，所以茫然多项式计算部分的计算复杂度为O((n-m)τ).另外，在安全近似模式匹配协议(协议3)的步骤2)中，发送消息的数量为2(n-m+1).在安全近似模式匹配协议(协议3)的步骤3)中，茫然多项式计算结束后，发送消息的数量为2(n-m+1).考虑到上述情况，安全近似模式匹配协议的通信复杂度为O(nm).

表2给出了本文中安全近似模式匹配协议与相关工作中半诚实敌手模型的近似模式匹配协议的比较结果.具体地，我们从协议的轮复杂度、计算复杂度、通信复杂度3个方面对协议进行效率比较.其中，n和m分别是模式匹配协议中数据库方与用户的输入长度，τ是给定阈值，λ是安全参数.

Table 2 Efficiency Comparison of Protocols表2 协议效率比较

首先，我们构造的协议同文献[5-6]的协议一样，只需要常数轮，优于文献[10]的协议的O(τ)轮.其次，文献[5-6]的协议主要使用同态加密技术，考虑到同态加密技术的高昂代价，因而文献[5-6]的协议的计算复杂度均为O(nm).文献[10]的协议中加密操作的数量级为O(mτ)，模幂操作的数量级为O(nτ)，因此文献[10]的协议的计算复杂度为O((n+m)τ).遗憾的是，文献[10，12]的协议在近似模式匹配过程中会泄露汉明距离.若考虑不泄露汉明距离的情况，文献[10，12]协议的计算复杂度和通信复杂度要比其所声称的更高.相较于文献[5-6，10]的协议，我们的协议在不泄露汉明距离的情况下实现了安全近似模式匹配，且计算复杂度仅为O(nτ).最后，考虑通信复杂度，我们的协议同文献[5-6，10]的协议相比较，通信复杂度较为接近.

4 性能评估

本节我们对安全近似模式匹配协议的性能进行评估.我们的协议是基于OT扩展、同态加密、茫然多项式计算以及PEQT构造的.其中，在OT阶段，我们使用OT扩展技术，只需要少量基础OT协议和一些对称操作就可以达到大量OT协议执行的效果，极大地减少了OT协议的数量.而高效的PEQT协议也可以通过基础OT协议和廉价的对称操作实现许多PEQT协议执行的效果.此外，Asharov等人[19]证明了OT扩展技术可以每秒执行数百万个OT实例，这是非常高效的.而加密、解密和模幂操作需要较长的执行时间，因此，在本协议中，我们主要考虑加密、解密和模幂操作的执行时间.

我们在运行Windows 10系统，使用Intel®CoreTMi5 CPU和16 GB RAM的个人计算机上进行我们的实验.在本实验中，我们使用随机的二进制模式字符串和文本字符串.此外，我们使用Paillier加密系统来进行加密，其密钥长度为2 048.

注意到，模式信息的长度记为m，文本信息的长度记为n，我们设置τ=0.5，即汉明距离需小于0.5 m.我们取模式的长度分别为m=26,27,28,29,210，文本的长度分别为n=211,212,213,214，协议运行时间如表3所示.我们可以发现，当模式长度为26、文本长度为212时，协议在10 s内即可运行结束.

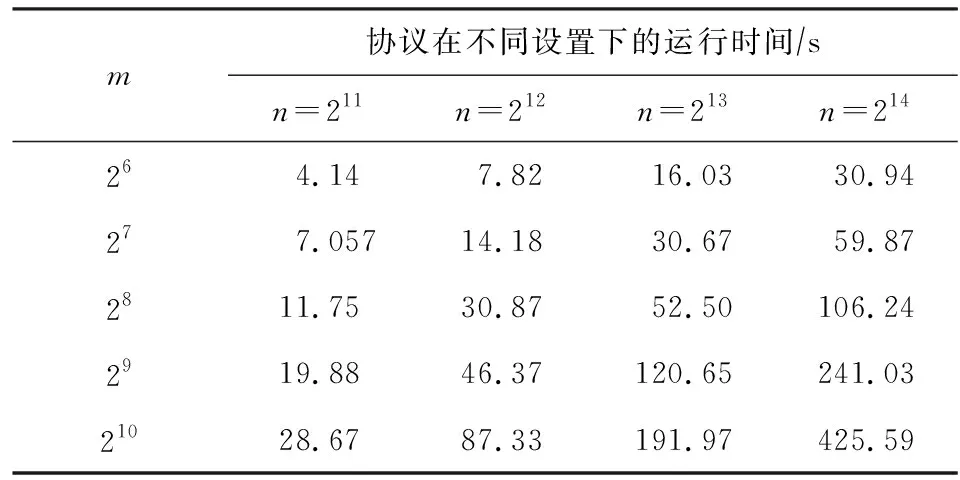
Table 3 Running Time of Different Settings at τ=0.5表3 τ=0.5时协议在不同设置下的运行时间

此外，我们又设置τ=0.9，模式长度m分别为26,27,28,29,210，文本长度n分别为211,212,213,214，并进行了实验.为了便于观察实验结果，我们给出了τ=0.5与τ=0.9时实验结果的折线图，如图2和图3所示.我们发现，当τ值由0.5增加到0.9，随着文本长度与模式长度的增加，协议的运行时间的增长幅度越大.

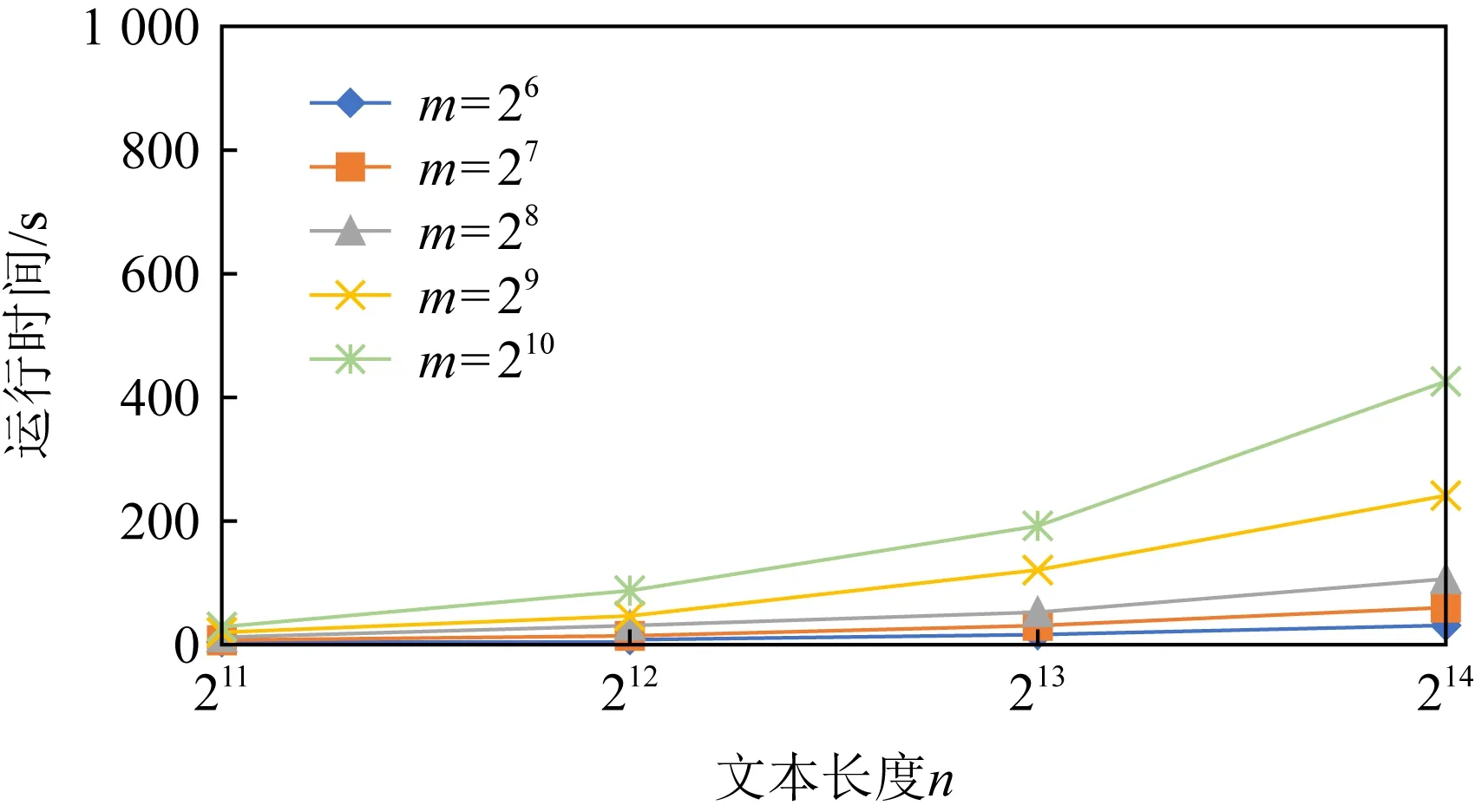
Fig. 2 Running time of different settings at τ=0.5图2 τ=0.5时协议在不同设置下的运行时间

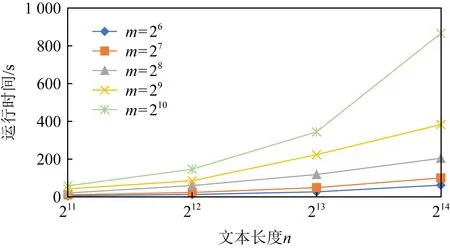
Fig. 3 Running time of different settings at τ=0.9图3 τ=0.9时协议在不同设置下的运行时间

5 结束语

本文主要考虑半诚实敌手模型下的高效安全近似模式匹配协议构造.协议主要是基于茫然传输、同态加密、茫然多项式计算以及隐私等值比较技术设计构造，需要常数轮交互，总体通信复杂度为O(nm)，计算复杂度为O(nτ)，其中n和m是数据库方和用户的输入长度, τ是近似匹配协议设定的阈值.在将来的工作中，我们将研究更为高效的近似模式匹配协议构造，并着重研究恶意敌手模型下安全模式匹配协议的构造.