多粒度融合驱动的超多视图分类方法

2022-08-12梁新彦钱宇华

计算机研究与发展 2022年8期

梁新彦钱宇华郭倩黄琴

(山西大学大数据科学与产业研究院太原 030006) (山西省机器视觉与数据挖掘工程研究中心太原 030006)

迅猛发展的表征学习技术和特征提取技术使得研究人员可以方便、容易地提取到数据不同视角的特征表示，进而可以更全面地认识数据、分析数据和管理数据.例如1张图片可以用尺度不变特征转换(scale invariant feature transform, SIFT)、局部二值模式(local binary pattern, LBP)、方向梯度直方图(histogram of direction gradient, HOG)等不同类型的特征描述；一段文本可以用汉语、英文、德文等语言描述；一段音频可以用梅尔倒谱系数(mel frequency vepstrum voefficient, MFCC)、语谱图(spectrogram)、过零率等不同类型的特征描述.

与单一视图特征相比，多视图数据可以提供更丰富、更多样的特征信息.在多视图数据的加持下，许多学习方法的性能得到了进一步的提升，如多视图分类[1-3]、多视图聚类[4-6]、多视图度量学习[7-9]、特征选择[10-12].此外，大量的应用也得到了进一步提升[13-15].其中，多视图分类方法由于广泛的应用场景，得到了越来越多学者的关注.

在多视图分类任务中，融合算子起着非常重要的作用[16]，因此设计有效的融合算子是这个研究领域的热点研究之一.早期的研究常常依据多视图分类方法中融合发生的阶段将其分为3类：早期融合、中期融合和后期融合.

本文的关注点也是融合算子.与现有工作的区别是本文研究如何更好地使用融合算子，而不是设计融合算子.为了我们的研究目的，本文依据多视图分类方法所使用的融合算子类型将其分为2类：基本融合算子和高级融合算子.

基本融合算子主要包括逐元素加、逐元素乘、逐元素平均、逐元素最大以及级联.其中，4个逐元素算子要求待融合的视图特征维度相同；级联会造成融合特征维度急剧增大.相比于高级融合算子，使用上述简单算子不会给模型带来额外的参数，同时，性能表现尚可.这些优势使得这些基本融合算子一直非常受欢迎，至今它们仍然被大量的研究工作所采用[17-20].

高级融合算子主要包括基于双向性和基于张量2种融合算子，其可以建模更多、更复杂的特征交互，其产生的融合向量表达能力趋向于更强.然而，由于这2类融合算子都是基于向量外积被提出的，导致基于它们实现的早期方法面临融合向量维度灾难问题.如图1所示，随着视图个数的增加，每个视图的特征维度急剧下降.例如，即使融合向量维度空间设置为100 000，对于包含5个视图特征的任务，在融合前，每个视图特征必须被压缩到10维，这必定会造成信息的严重缺失.因此，这些高级融合算子几乎只在视图个数较少的场景中被使用.例如，情感分析(3个视图)[21]、细粒度图像识别(2个视图)[22]、视觉问答(2个视图)[23-24].然而，在实际应用中，存在许多包含超多视图(视图个数大于3时称为超多视图)的场景.比如，在文献[25]分析的多语言分类任务中，每个文本被5种语言视图特征描述；在文献[15，26，27]的图像识别任务中，每张图片分别被10个视图特征、7个视图特征和6个视图特征描述.尽管基于高级融合算子多视图学习方法在包含3个及以下视图任务上取得极大成功，然而当视图个数较多时，它们的表现有待提升.

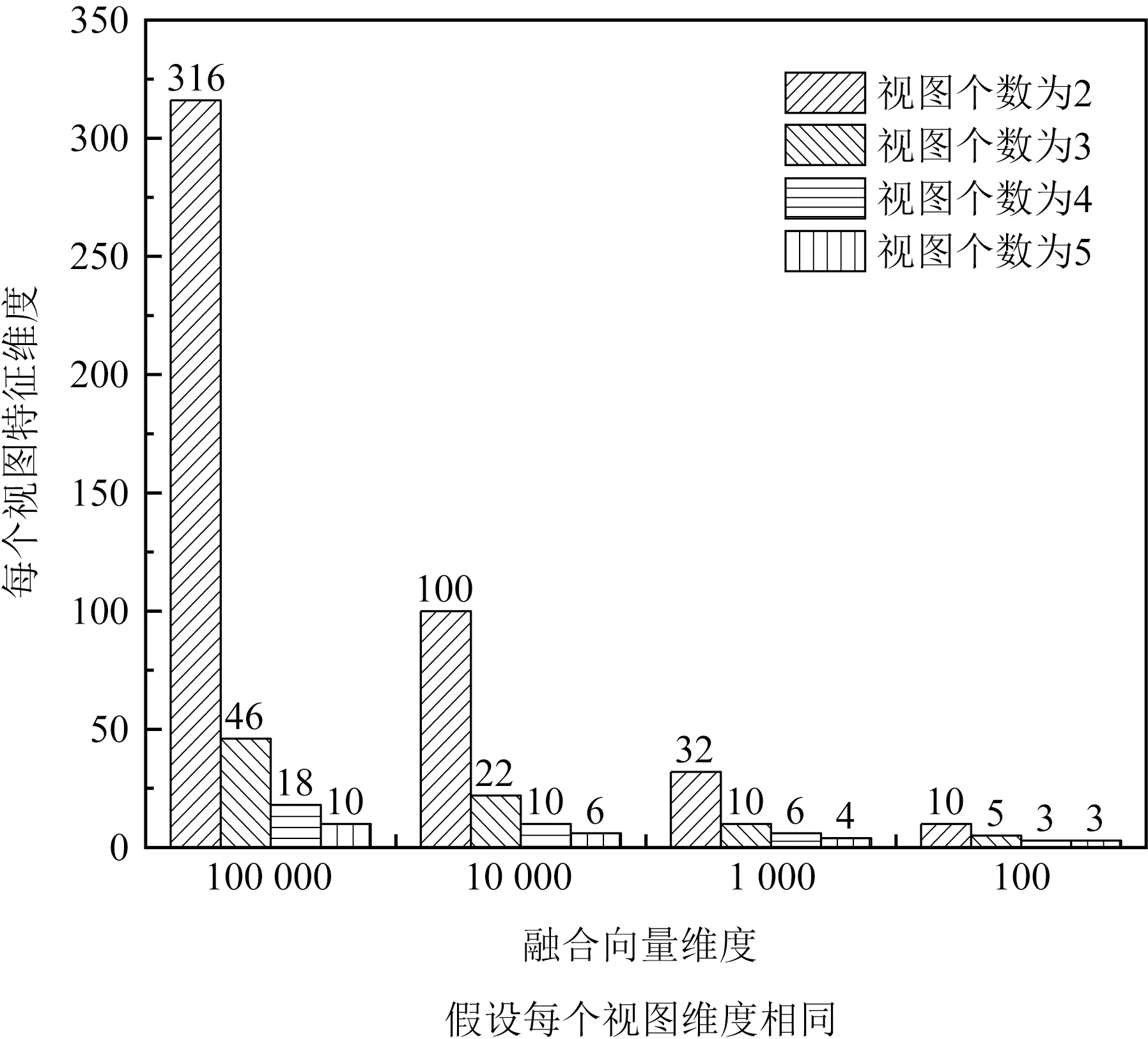
Fig. 1 Relation between the dimension of fused vector and dimension of views图1 融合向量维度和每个视图特征维度间的关系

总的来说，现有方法中存在2个问题：

1) 如图1所示，由于张量的融合算子导致融合向量维度灾难问题，导致基于它的方法难以推广到包含更多视图的应用中.

2) 如图2(a)所示，现有多视图分类方法趋于使用某种融合算子直接作用于全部视图特征，一次得到最终的融合向量.当视图数量较多时，这种策略对于有效建模不同视图的关系较困难.

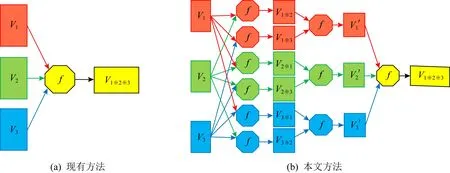
Fig. 2 Difference between existing methods and our method图2 现有方法与本文方法的差异

人类的多粒度认知能力是求解复杂问题、分析复杂数据的一种有效策略，为我们从多视角、多层次建模数据提供了一个新的视角和方法.多粒度粗糙建模[28]是对人类多粒度认知能力的一种有效模拟实现，借助于它，我们可以灵活地在不同粒度水平上管理、分析、认识数据.特别地，当对数据认识不足时，我们可以在一个较粗粒度水平下分析数据；随着对数据的了解，可以在一个更细粒度水平下处理数据.图3展示了在多粒度建模背景下7种生物从2个视角和3个层次进行分类的示意图.其中，平面AOB和BOC分别表示分类7种生物的一个视角，蓝色、橙色和黄色分别表示分类7种生物的一个层次，其具体语义如图3(a)所示.每个视角、层次下的分类结果对应于粒度建模理论中的1个粒结构，显然本例中共包含6个粒结构，如图3(b)所示.在同一视角下，不同层次下构建的粒结构具有偏序关系；同一层次下，不同视角下构建的粒结构间通常不具有偏序关系.显然，多粒度建模是一种比多视角和多层次更一般的建模理论，多视角和多层次都是它的特殊情况.

受多粒度思想的启发，本文提出一种基于多粒度融合的超多视图分类方法.正如图2所示，与使用1个融合算子直接作用于全部视图特征融合得到最终的融合向量的方法不同，本文所提方法在3个粒度水平上，由易到难分层实现多视图特征融合.具体来说，本文方法首先建模任意2个视图对之间的关系；然后，基于成对关系结果，建模每个视图与其他全部视图的关系；最后，基于每个视图与其他全部视图的关系结果，建模全部视图间的关系.

本文工作的主要贡献包括3个方面：

1) 将多粒度建模思想引入到多视图机器学习中，提出一种多视图数据的多粒度空间构造方法；

2) 基于构造的多视图多粒度空间，提出了一种多粒度融合方法(multi-granulation fusion method, MGF)，该方法从视图对、每个视图和其他全部视图与全部视图3个粒度水平上由易到难分层实现多视图特征融合；

3) 在4个超多视图数据集上的实验结果表明MGF方法可以有效融合更多的视图，验证了本文方法的有效性.

1 相关工作

1.1 多粒度建模

人类的多粒度认知能力是求解复杂问题、分析复杂数据的一种有效策略[29].多粒度认知为我们从多视角、多层次、多粒度建模数据提供了一个新的视角和方法.借助于它，我们可以灵活地在不同粒度水平上管理、分析、认识数据.由于多粒度思想的普适性，目前，它已经被成功应用于不同领域.通常，不同领域有其特有的多粒度空间构造方法.比如，在粒计算领域，可以通过同时使用诸如等价关系、邻域关系、相容关系等多种二元关系来构造特征空间的多粒度结构；在计算机视觉领域，空间金字塔、多尺度等技术可用于获取图片的多粒度结构；在自然语言处理领域，可以分别从字符、词、句子、段落等表示来构造语言的多粒度结构；在语音处理领域，可以使用不同采样率获取的音频构造其多粒度结构.事实上，对于不同领域，一个通用的获取多粒度空间的方法是基于数据的多个视图表示，通过将每个视图看作数据的一个粒度.可见多视图特征是数据的一个典型多粒度表示.本文的目的是通过重新分组现有的特征组来构造一个有效的多粒度融合空间，融合发生在每个粒度空间，以达到更有效的多视图融合.

1.2 多视图分类

给定一个多视图数据集，其中每个样本同时被多个特征集V={v1,v2,…,vm}所描述，其中，vi表示第i个视图的特征集，m表示视图个数.基于多视图数据学习的分类任务称为多视图分类.其旨在通过融合多个视图的信息来提升模型的分类性能.不同视图的融合过程可以简单形式化为

c=f(g1(v1),g2(v2),…,gm(vm)),

(1)

其中，f表示一个融合算子，例如逐元素加，级联，张量乘积；gi表示对每个视图的映射函数，比如，当f为逐元素加时，gi可以将不同维度的视图特征映射为相同维度大小，以便f可以有效工作.

依据融合视图过程中所使用的融合算子f类型，大致分为2类：基于简单融合算子的方法和基于先进融合算子的方法.

1) 基本融合算子

基本融合算子包括逐元素加、逐元素乘、逐元素平均、逐元素最大以及级联.它们可以形式化表示为

① 逐元素加：c=v1+v2+…+v|V|；

② 逐元素乘：c=v1∘v2∘…∘v|V|;

③ 逐元素平均：c= (v1+v2+…+v|V|)/|V|;

④ 逐元素最大：c=max(v1,v2,…,v|V|);

⑤ 级联：c=[v1,v2,…,v|V|].

由于基本融合算子具有融合维度紧凑(逐元素运算融合向量维度不会增大，级联运算融合向量维度线性增大)，计算代价较小等优势而被广泛使用.例如，Wang等人[17]提出了ARTNets用于分类视频，该方法通过级联融合算子融合不同视图的特征，然后，将级联的特征向量输入到一个分类器中.但这类方法在建模特征交互方面的能力不强.

2) 高级融合算子

为了增强特征间的交互作用，双向性融合算子和张量融合算子被引进到多视图机器学习中.

① 基于双向性融合方法.双向性聚合算子通过使用外积运算来建模不同视图间的关系.Kim等人[23]提出了多模态低秩双向性聚合(multi-modal low-rank bilinear pooling, MLB).该方法首先将每个视图映射到一个低维空间，然后使用逐元素乘算子来聚合全部的低维向量，最后通过一个低秩矩阵来将聚合的向量映射为最终的融合向量.这个过程可形式化为

(2)

进一步，Yu等人[24]通过引入一个和聚合函数来增强MLB融合向量的表达能力.这个过程被形式化为

(3)

其中，SumPool(x,k)表示和聚合函数，它通过一个大小为k的非重叠的窗口来聚合x中元素.

② 基于张量融合方法.代表性的工作包括:张量融合网络(tensor fusion network, TFN)[30]、低秩多模态融合(low-rank multi-modal fusion, LMF)[31]和多项式张量聚合(polynomial tensor pooling, PTP)[21].

TFN融合不同的视图：

(4)

其中，⊗表示克罗内克积，W∈(m1+1)×(m2+1)×…×(m|V|+1).当视图个数|V|很多时，W是一个非常高维的参数张量，这导致TFN训练需要非常大的内存开销，有时甚至由于内存限制不能被训练.

为缓解W造成的维度灾难问题，Liu等人[31]提出了低秩多视图融合方法，这个过程可以形式化为

(5)

注意到LMF最多可以考虑不同视图特征的二阶交互，Hou等人[21]提出了一个可以建模P阶特征交互的多项式张量融合方法，这个过程可以形式化为

(6)

其中，f=[v1,v2,…,v|V|]，P表示建模特征的阶数.

2 多粒度融合驱动的多视图分类方法

2.1 框架概述

为了实现超多视图的融合，本文提出了一种多粒度融合驱动的多视图分类方法(multi-granulation fusion method, MGF),模型框架如图4所示.

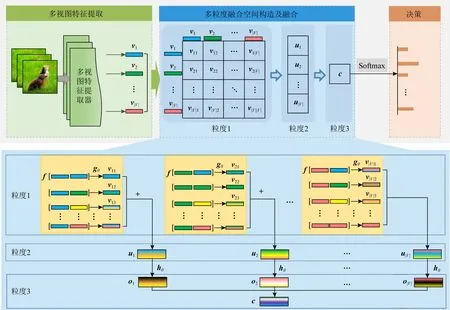
Fig. 4 Model architecture图4 模型架构图

本节我们将详细介绍本文提出MGF方法.如图4所示，MGF方法由3个模块组成：多视图特征提取、多粒度融合空间构造及融合和决策.下面，将依次介绍每个模块的功能及工作原理.

2.2 多视图特征提取

如图4所示，多视图特征提取模块主要目的是借助于不同的特征提取器，如SIFT，HOG，CNNs提取图片、文本等数据的不同类型特征.提取的多视图特征将被输入到基于多粒度的多视图特征融合模块中用于后续的融合.为了消除特征提取给实验结果带来的影响，本文实验使用了4个提供了多视图特征的超多视图数据集用于比较研究.

2.3 多粒度融合空间构造及融合

基于多粒度的多视图特征融合模块是MGF方法的核心.该模块的主要目的是在不同粒度水平上对视图特征进行逐层融合.该模块学习人类在求解复杂问题时所采用的多粒度认知行为——将原问题分层求解，不同粒度之间互相关联，且不同粒度之间可以自由转换——将现有方法采用的直接融合全部视图的策略改为分层融合策略以实现更有效的视图融合.当视图个数较少时，视图间的关系更容易建模，此时，有大量的融合算子可供选择.因此，基于分而治之的思想，我们将全部视图的融合分解为3部分视图融合，本文构造了一个具有分层结构的3粒度融合空间.如图5所示，这个融合空间依次从视图对、当前视图和其他视图与全部视图3个视角构造粒度空间，在这3个不同粒度水平上可以对视图特征进行由简到易分层融合.多粒度融合空间构造的核心思想为：当前层的融合空间考虑的对象要比后一层简单，且通过融合算子可以转化到下一层的融合空间；当前层的融合依赖于前一层的融合结果.

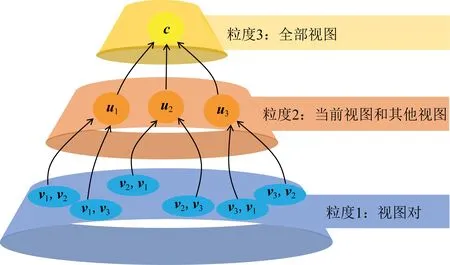
Fig. 5 A three granularity space for multi-view fusion图5 多视图融合的一个3粒度空间

具体地说，给定1个多视图特征集合V={v1,v2,…,v|V|}，其中，vi表示第i个视图的特征，|V|表示视图个数.首先，在第1个粒度上，MGF考虑所有视图对(vi，vj)之间的融合，相比于直接建模全部视图之间的关系，建模视图对之间的关系更容易；其次，在第2个粒度上，MGF通过逐元素加融合算子建模每个视图vi与其他视图v1,v2,…,v|V|之间的关系oi；最后，在第3个粒度上，使用逐元素加融合算子建模全部视图o1,o2,…,o|V|间的关系.其中，n为样本总数.

基于多粒度的多视图特征融合和决策模块包括4个步骤：

步骤1.在粒度1(视图对)水平下，按照式(7)融合每一对视图(vi，vj).

vij=gθ(f(vi,vj)).

(7)

步骤2.在粒度2(每个视图与其他全部视图粒度)水平下，利用在粒度1水平下得到的视图对融合结果，首先使用逐元素加聚合视图i与其他视图，得到它们间的融合结果ui:

ui=vi1+vi2+…+vi|V|,

(8)

然后，使用函数hθ对聚合结果ui进行深度融合:

oi=hθ(ui).

(9)

步骤3.在粒度3(全部视图粒度)水平下，使用逐元素加融合算子聚合在粒度2水平下得到的每个视图与其他视图间融合的结果，得到视图v1,v2,…,v|V|最终的融合结果c:

c=o1+o2+…+o|V|,

(10)

由于参与融合的oi较多，融合结果c的变化范围也很大，因此，将c进行规范化操作.

步骤4.规范化c:

(11)

(12)

其中，sgn表示符号位函数.式(11)表示幂律归一化(power-law normalization)；式(12)表示L2范数归一化(L2 normalization)，在多模态数据融合过程中，这2个公式常被联合用于缓解融合向量波动值范围较大的情况.

2.4 决策

如图4所示，分类模块的目的是将融合向量映射到决策空间，对多视图数据完成分类.使用1个全连接层(fully-connected layer,FC)和softmax函数将融合向量c映射到1个概率向量，得到每个样本属于每类的概率.也即：

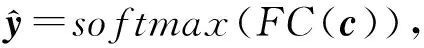
(13)

其中，softmax函数定义为

(14)

其中，z=FC(c)是1个长度为k的向量，k为类别数.

MGF通过随机梯度下降法进行优化求解，定义的交叉熵作为损失函数:

(15)

其中，n为样本总数.

对于MGF需要说明3点：

1) 在粒度1水平下，视图对间的融合较容易，因此，用于视图对间的融合算子f的选择较多，理论上，现有的融合算子都可以使用.

2) 在粒度2和粒度3水平下，待融合的向量较多，不宜选择产生额外参数的融合算子.因此本文使用逐元素加融合算子.

3) 在粒度1和粒度2中使用的深度融合函数gθ和hθ作用的对象为融合后的向量，对其进一步的融合带来很少的参数.本文中，它们通过1个多层感知机来实现.

3 实验

3.1 实验设置

本文所有方法使用Tensorflow实现.计算环境是Ubuntu 16.04.4，512GB DDR4 RDIMM，2X 40-Core Intel®Xeon®CPU E5-2698 v4 @2.20 GHz, NVIDIA Tesla P100,显存16 GB.

所有模型采用相同的训练设置.具体来说，使用Adam优化器，其学习率设置为0.001.每个模型训练100轮(epoch)，如果一个模型的性能在10个epoch内没有提升则训练结束.

3.2 数据集

本文实验使用4个超多视图基准数据集：Chekbook-10k(CB)[15]，Ainimal with Attributes(AWA)[26]，NUS-WIDE(NUS)[27]和Reuters[25]，它们的统计信息如表1 所示.

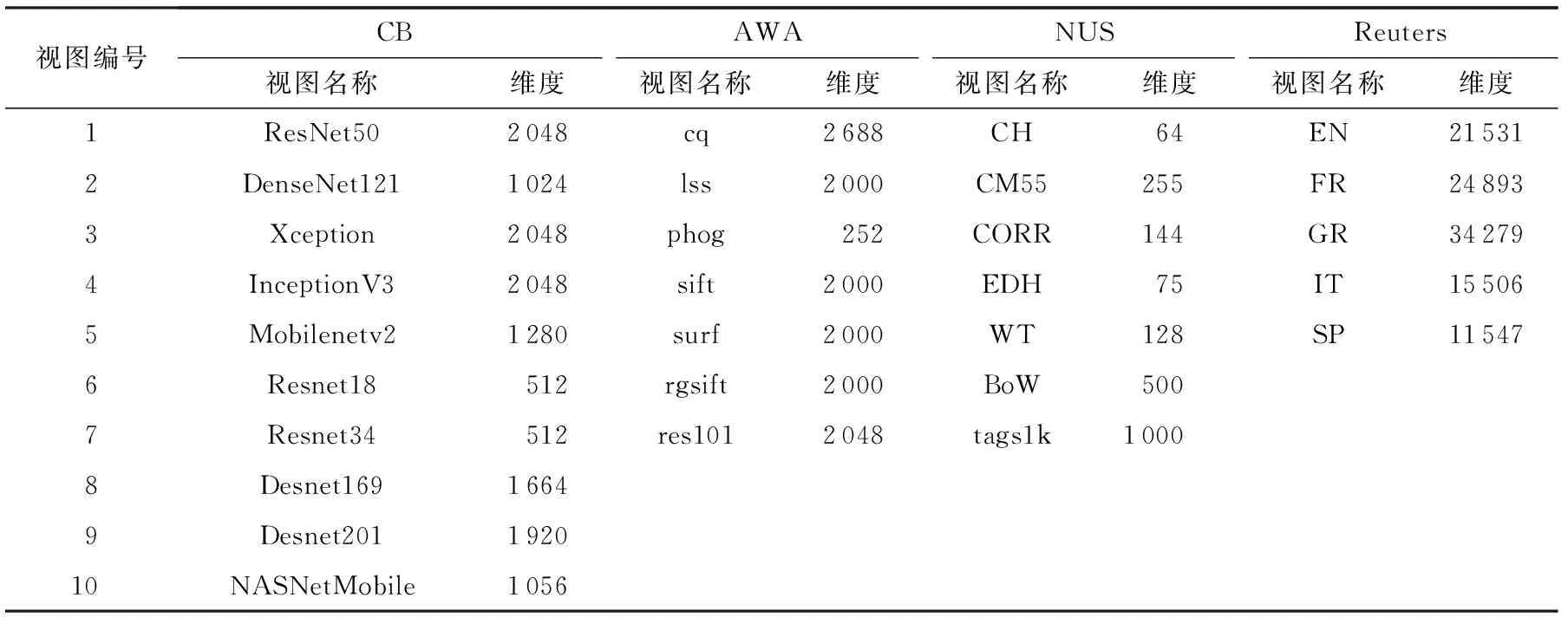
Table 1 Statistic Information of Datasets表1 数据集统计信息

CB[15]是1个化学结构识别的多视图数据集，包含10万张化学结构图片，属于10 000类，每类包含10张图片，每张图片由10个深度特征描述.

AWA[26]是一个包含50种动物的多视图数据集，包含30 475张动物图片，每张图片由7个视图特征描述.

NUS[27]由23 438张图片组成，每张图片由6个图片相关的视图特征和1个文本相关的视图特征描述，它们被分成10类.

Reuters[25]是一个包含111 740条文本，每条文本由5种语言描述的多视图文本分类数据集.

各个数据的各个视图的分类性能如图6所示.从图6可以看出，CB和Reuters数据集中每个视图性能都可以获得较好的性能，AWA中深度特征性能要远远好于其他手工特征，NUS中语义特征tags1k远远好于其他手工特征.

Fig. 6 Experimental results for single view on four datasets图6 4个数据集上单视图实验结果

为减少数据集划分与模型训练随机性带来的影响，所有数据集按照8∶2(训练集:测试集)的比例随机划分5次.每个方法在5个划分数据集上的平均性能和标准差将被报告.

3.3 比较方法

本文方法分别与14个多视图方法进行比较研究，包括3个集成学习方法、5个多视图基线方法和6个最先进的多视图方法.

1) 3个集成学习方法

① Best.使用每个视图训练1个模型，选择性能最好的模型作为最终融合模型.

② SSV(simple soft voting).使用每个视图训练一个模型，简单平均全部模型的概率输出结果作为最终的融合结果.

③ MR(maximum rule).使用每个视图训练一个模型，选择全部模型中最高置信度值的输出结果作为最终的融合结果.

2) 5个多视图分类基线方法：逐元素加(Addition)、逐元素平均(Average)、逐元素最大(Max)、逐元素乘(Multiplication)和级联(Concatenation)

3) 6个最先进的多视图分类方法

① MLB[23].它是基于双线性聚合的方法，通过|V|+1个矩阵乘积运算近似|V|个向量的外积运算来缓解融合向量维度灾难问题.超参数m被设置为128，d依次从{64，128，256，512}取值.

② MFB[24].它是MLB一个增强方法，在MLB使用|V|个矩阵将每个视图特征映射到低维空间后，通过引用一个带有无重叠一维窗口的和聚合函数来提升每个映射向量的表达能力，然后再使用逐元素乘积融合算子聚合它们.超参数m设置为128，k依次从{1,2,3,4,5}取值.

③ TFN[28].首先将每个视图特征与常数“1”进行拼接，然后使用外积依次融合每一个拼接后的视图特征.用这种方式显示建模单视图、2个视图，…，|V|个视图之间的交互.超参数m设置为128，mi依次从{2,4,6,8}取值.

④ LMF[30]. 它通过带有视图私有的因子的低秩多模态完成视图融合.m设置为128，mi设置为128，r依次从{2,4,6,8}取值.

⑤ PTP[21].不同于其他直接使用外积融合不同的视图特征，PTP先级联全部视图特征，然后计算级联向量的张量积.超参数m设置为128，mi依次从{16,32,64}取值，p依次从{1,2,3}取值.

⑥ EmbraceNet[32].它是一个对缺失视图数据鲁棒的方法.首先将不同视图映射到相同维度的向量，然后，随机选择一个视图中第i位置的元素作为融合向量第i位置的值.重复该过程，选择出融合向量的全部位置的值.在实验中，每个视图被选择的概率值p设置为1/|V|.

3.4 评价指标

本文使用准确度(Acc)和卡帕(Kappa)这2个指标来评价方法的性能.

Acc是分类任务常用的指标，然而对于样本不平衡、噪声干扰的数据集，分类方法易出现随机一致性问题[33].此时，准确度指标不能真实反映出方法的性能.因此，本文也采用了更公平的kappa指标.这2个指标的定义可以基于表2的混淆矩阵诱导出.

Acc的定义为

Table 2 Confusion Matrix表2 混淆矩阵

(16)

Kappa指标的定义为

(17)

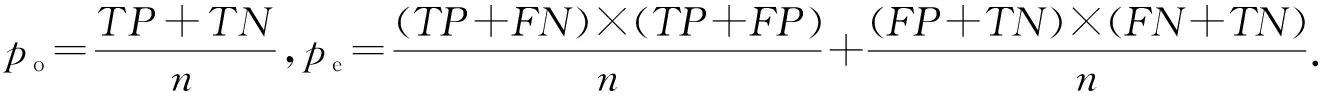
这2个评价指标的值越大，方法性能越好.

3.5 实验结果及分析

本文所提方法与14种对比方法在4个数据集上的实验结果如表3和表4所示.其中，最好的结果使用粗体标记，+，=，-分别表示在成对t-test下MGF在95%的置信水平显著好于、持平和差于对应的比较方法.

实验结果如表3和表4所示，在CB，AWA和NUS数据集上，MGF排在第1名，在准确度指标上比第2名分别高2.56%，1.08%和0.33%；在kappa指标上分别高2.56%，1.11%和0.34%.在Reuters数据集上，MGF方法排在第2名，在准确度和Kappa指标上比第3名分别高1.80%和2.15%.在Reuters数据集，SSV 表现优于MGF，这主要是由于它们的训练策略.具体来说，相比于其他数据集，Reuters数据集的每个视图特征维度极大，最小维度为11 547，最大维度为34 279. SSV首先在每个视图上单独训练一个模型，然后平均|V|个模型的分类概率值作为融合模型的得分概率.然而，MGF需全部视图特征都参与训练，高维的视图特征给模型带来了大量的参数，导致模型训练困难.然而，方法MGF仍然取得了采用同类融合策略方法中的第1名.此外，就平均准确度指标而言，MGF取得84.68%，排名第1，比排在第2名的MFB方法高1.67%.再者，根据成对t-test，MGF在112个不同实验设置下(14个对比方法、2个评价指标、4个数据集)，在95%的置信水平显著好于对比方法的次数为106，持平次数为4，差于对比方法的次数为2.这些结果清晰表明本文提出的MGF方法的性能统计上优于对比方法，证明多粒度融合策略在多视图分类任务上确实有用.

Table 3 Accuracy Results (Mean±Standard Deviation) Among Different Comparative Methods on Four Datasets表3 不同方法在4个数据集上的准确度比较(均值±标准差)

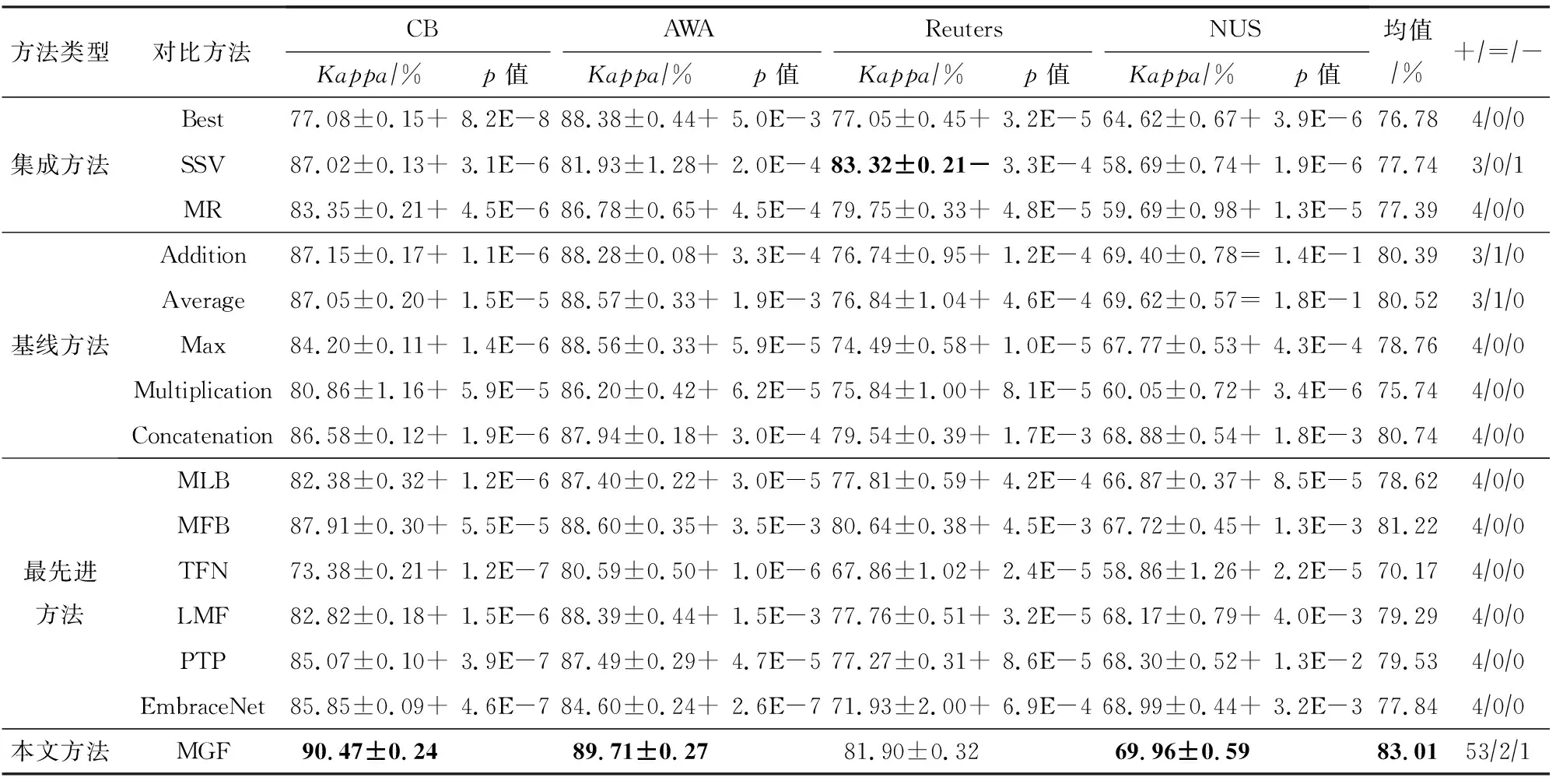
Table 4 Kappa Results (Mean±Standard Deviation) Among Different Comparative Methods on Four Fatasets表4 不同方法在4个数据集上的Kappa值比较(均值±标准差)

此外，在视图个数较大的场景下，采用高级融合算子的方法无法获得理想结果.它们的性能甚至比采用简单融合算子的方法还差，这主要是因为简单融合算子(级联除外)不会引入额外参数，然而，高级融合算子会引入额外的参数，且参数量会随着视图个数的增加而增大，增大了这些模型过拟合的风险.

为了从统计上验证MGF的有效性，基于表3和4实验数据，通过统计每个方法显著性优于与显著性差于其他方法的次数之间的差值来分析每个方法的统计性能[34].具体地说，给定2个方法a和b，假设它们分别在同一数据集上运行n次， 2个方法n次实验结果的均值分别表示为μa与μb，方差分别表示为σa与σb.如果满足：

(18)

那么方法a显著性优于方法b，否则方法a显著性差于方法b.

如图7所示，方法MGF的条形图最高，表明它的性能显著性优于其他对比方法.此外，注意到TFN方法的负半轴最高，表明其性能显著性差于其他方法，这进一步验证了视图维度的过度压缩会导致性能的严重退化.因此，那些会导致融合向量维度急剧增大的方法不适用于视图个数过多的情景.

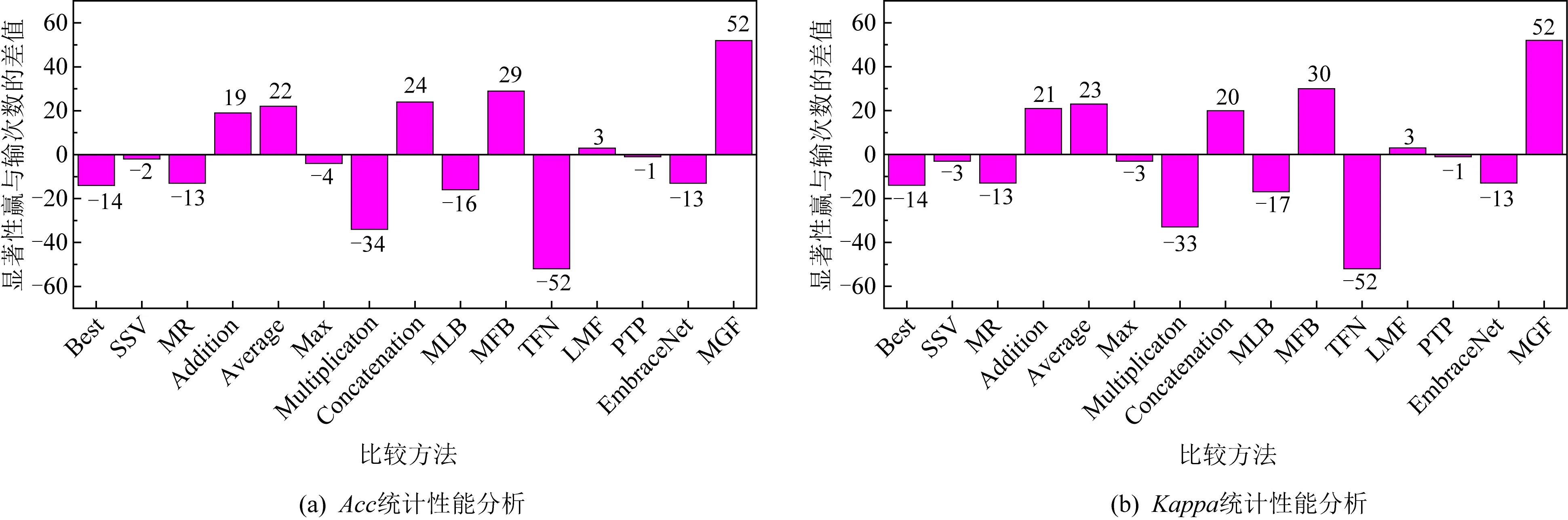
Fig. 7 Significant difference comparison of Acc and Kappa图7 ACC和Kappa显著性差异比较

总体来说，大量的实验验证了方法MGF的有效性.这些结果表明，分层融合策略确实可行.

与其他对比方法相比，MGF方法由于采用在多个粒度下对视图信息进行融合的策略，导致其会引入额外的学习参数.因此，我们分析、比较了所有方法的可学习参数量和训练时间，实验结果如图8所示.从中可以发现，在4个数据集上，逐元素加(addition)和级联(concat)方法学习参数量和训练时间都是较少的.虽然MGF的学习参数量和训练时间比基于逐元素加(addition)和级联(concat)算子的多视图方法要多和长.但是，由于它只使用这2种融合算子，与一些基于张量的融合算子方法如TFB相比，它的学习参数量和训练时间都是可接受的.

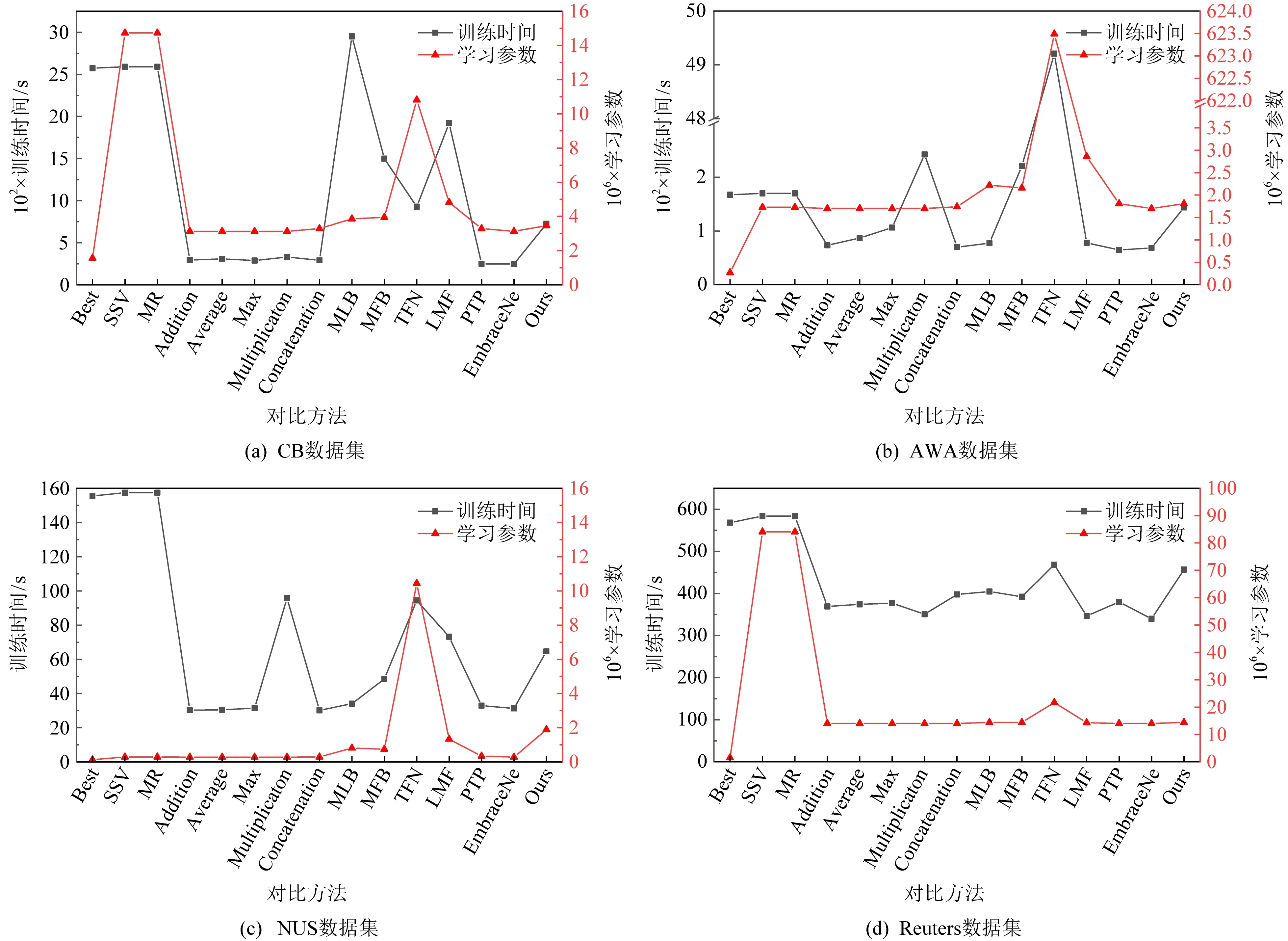
Fig. 8 Comparison of parameters and training time among different methods图8 不同方法的学习参数和训练时间对比情况

3.6 进一步分析

本节旨在研究融合维度大小和不同粒度层中融合算子的选择对MGF方法的影响.

1) 融合维度影响分析

本实验对融合维度设置为64，128，256及512的MGF方法的实验性能进行比较，实验结果如图9所示，从中可以看出：对于数据集CB和NUS，随着融合维度增大，MGF的准确度增加.例如在CB数据集上，融合维度512的MGF要比64的MGF的准确度值提高了91.96%-87.95%=4.01%，在AWA和Reuters数据集上，准确度值随融合维度的增大变化较小，图9(b)和(d)出现的波动可能是随机性造成的，例如对于AWA数据，当融入维度由128变为256时，MGF模型性能提高了89.82%-89.71%=0.11%，而当融入维度由256变为512时，性能下降了89.82%-89.65%=0.17%.上述实验结果表明不同的数据集对于融合维度的敏感性是不同的，因此使用交叉验证选择合适的融合维度值是一个不错的策略.

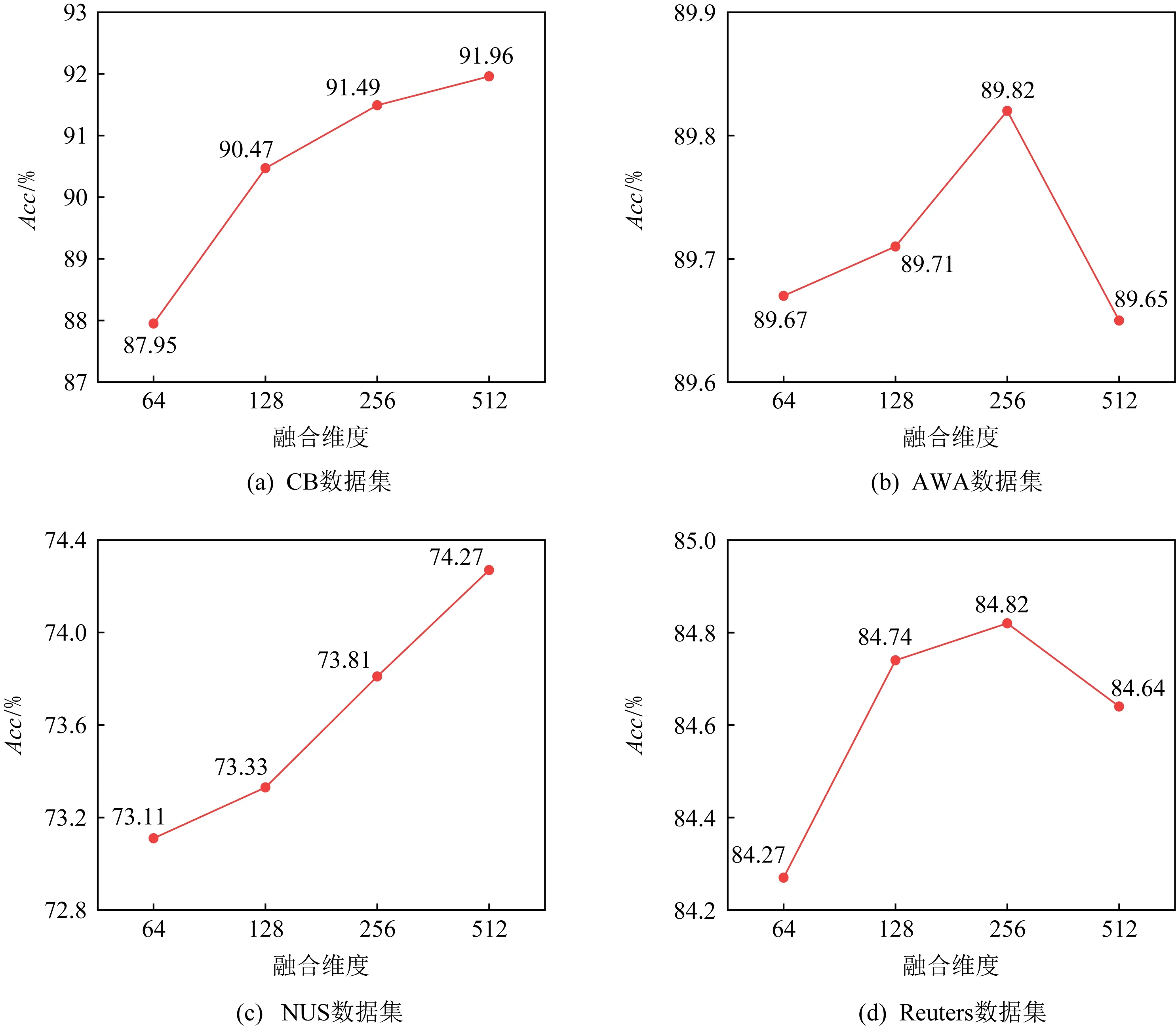
Fig. 9 Change of accuracy with the dimension of fused vector图9 Acc随融合维度取值的变化情况

2) 融合算子影响分析

本部分旨在研究在不同粒度层上融合算子的选择对MGF方法的影响，实验结果如图10所示.

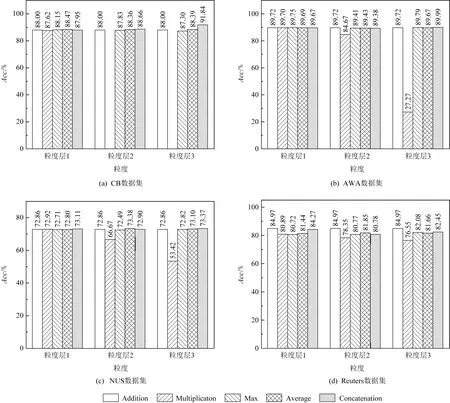
Fig. 10 The relation between fusion operator adopted by the first, second and third granularities and accuracy图10 粒度层1，2，3所采用融合算子与分类准确度之间的关系

实验设置：融合维度设置为64，选择Addition，Mul，Max，Average和Concat这5种基本融合算子用于实验比较.MGF方法包含3个粒度层，每个粒度层可从5种融合算子任取一种，共125种情况，为了缓解随机性对实验结果的影响，每种参数组合的MGF方法都运行5次，报告5次结果的均值，因此MGF方法需在每个数据集上运行625次.为了缓解参数组合太多的问题，采用“固定变量法”策略，即改变一个粒度层中的融合算子，固定其他粒度层中的融合算子.实验分为3组：①粒度1改变，粒度2和3固定选取Addition融合算子；②粒度2改变，粒度1和3固定选取Addition融合算子；③粒度3改变，粒度1和2固定选取Addition融合算子.实验结果如图10所示，其中每个子图横坐标轴上粒度1、粒度2和粒度3分别对应上述3组实验.

从图10中可知：①Mul算子对MGF的性能影响最大，特别是涉及的待融合元素较多时，比如当MGF中粒度层2，3采用Mul时，其分类性能几乎为0.这是由于当融合视图数量是10时，1个标量需要与其他9个标量进行9次乘法运算，这将导致信息消失或者弥散，进而引起模型训练崩塌.②Addition融合算子在4个数据集、3个粒度层上都表现出了有竞争力的性能，这反映了加运算可以增强信号，这也与文献[15]中对EDF搜索发现的融合网络中所使用融合算子的频次统计结论一致.