点云配准中多维度信息融合的特征挖掘方法

武 越 苑咏哲 岳铭煜 公茂果 李 豪 张明阳 马文萍 苗启广

1(西安电子科技大学计算机科学与技术学院 西安 710071)2(西安电子科技大学电子工程学院 西安 710071)3(西安电子科技大学人工智能学院 西安 710071)

随着三维数据采集技术的快速发展，激光雷达[1-2]、结构光传感器和立体摄像机采集到的点云数据得到了广泛应用.同时，这也使得点云配准、分类、分割等应用引起了广泛关注.三维刚体点云配准是计算机视觉和机器人学[3-4]等许多重要应用中的一项关键任务，如自动驾驶[5-6]、手术导航和同步定位与构图(simultaneous localization and mapping, SLAM)[7]等.点云配准的目的是找到一个刚性变换将一个点云与另一个点云对齐.然而，点云固有的结构缺陷给其直接应用于深度学习体系带来了很大的困难.PointNet[8]及其变体的出现给点云提供了结构化表示方法，可以克服直接在深度学习中使用点云的困难，并且极大地提高了处理速度.

传统的点云配准方法，例如迭代最近点(iterative closest point, ICP)算法[9]以及基于ICP的衍生算法[10-14]，它们通过寻找2个点云的对应点关系来估计刚体变换[15].但是，它们对初始化极其敏感，配准通常会在寻找最优解的过程中陷入局部最优而失败[16].近年来，研究者们提出了许多基于PointNet的深度学习的无对应点云配准方法，它们通过PointNet提取全局特征描述符，为后续刚体变换阶段提供获取精确变换参数的基础.然而，这些深度学习方法在提取全局特征时容易忽略低维局部特征，导致大量点云信息的丢失，使得后续刚体变换估计阶段求解变换参数时精度无法达到预期[17-21].

数据挖掘是使用人工智能等方法在大型数据集中提取隐含潜在信息的过程.数据挖掘已经广泛存在于人工智能的应用当中，例如计算机视觉、自然语言处理和推荐系统等.深度学习作为人工智能领域中一种基于对大数据进行表征学习的方法，其可以自动从大量信息中获取有价值的知识，充分挖掘隐藏在大数据中的丰富信息，从而完成如分类、回归等特定任务.本文将数据挖掘应用于点云配准当中，通过深度学习设计了基于多维度信息融合的特征挖掘方法，充分挖掘点云中的高维全局和低维局部信息，有效弥补了点云配准的全局特征提取阶段局部特征的缺失.

本文的主要贡献包括3个方面:

1) 提出了一种多维度信息融合网络(multi-dimensional information fusion network, MIFNet)，充分挖掘点云中的高维全局和低维局部信息，有效弥补了点云配准的全局特征提取阶段局部特征的缺失;

2) 为了充分挖掘变换信息，在刚体变换估计阶段使用了深度神经网络拟合对偶四元数的刚体变换参数，其可以在一个公共框架内同时表示旋转和平移，为姿态估计提供紧凑和精确的表示;

3) 在ModelNet40数据集上进行了大量实验，结果表明：与现有无对应前沿的无对应点云配准方法相比，我们的方法可以获得更高的精度，同时对噪声具有较强的鲁棒性.

1 相关工作

目前的文献中描述了许多先进的点云配准方法.经典的传统点云配准方法需要良好的初始变换，并在初始点附近收敛到局部最小值.最有代表性的方法是ICP算法，该算法从初始变换开始，迭代交替求解2个子问题：在当前变换下寻找最接近的点作为对应点以及通过奇异值分解(singular value decomposition, SVD)找到对应计算的最优变换.尽管ICP可以完成较高精度的配准，但它容易受到初始扰动的影响.近年来，人们基于ICP提出了各种衍生的变体，可以改善ICP的缺陷，提高配准精度.然而，仍存在一些基本的缺点.首先，它们强烈依赖于初始化.其次，由于它们不可微分的性质，很难将它们整合到深度学习系统中.

PointNet是第1个直接将点云应用在深度学习系统中的方法，它通过对称函数解决了点云的无序性.PointNet为下游任务提供了一个非常有用的概念，用于提取点云的特征，并激发了研究者们使用深度学习解决点云配准问题的兴趣.基于深度学习的方法通常分为基于对应的方法和无对应的方法.基于对应关系的方法占据了相当大的比例，如CorsNet[22],DeepVCP[23]和3DFeat Net[24-26]等.而基于无对应的方法较少，是目前研究的一个热点.无对应方法通过计算2个点云的全局特征之间的差异来获得刚体变换参数.与传统方法和基于对应的方法相比，该方法节省了搜索对应点的时间.例如PointNetLK[27]和PCRNet[28]在内的无对应点云配准方法使用PointNet作为特征提取器[29].PointNetLK通过PointNet计算全局特征描述符，并迭代使用逆合成公式和光流(Lucas-Kanade, LK)[30-31]算法最小化描述符之间的距离以实现配准.PCRNet使用数据驱动技术代替PointNetLK中的逆合成公式和LK算法进行特征对齐，该算法对训练中未见过的形状可以产生良好的泛化能力[32].然而，这些方法在特征提取过程中忽略了局部信息，导致大量点云信息的丢失，因此我们本文针对此问题进行了改进.

另外，在刚体变换估计阶段，有许多方法可以表示具有3个自由度的刚体的旋转，例如旋转矩阵、旋转向量和欧拉角[33].旋转矩阵由9个变量表示，这种方法表示是冗余的.旋转矢量和欧拉角是紧凑的，但它们存在万向锁问题[34]，并且容易出现奇异性.为了解决这个问题，Hamilton在1866年提出了一个扩展复数，并将其命名为四元数[35]，它可以将复数扩展到三维空间.四元数完美地解决了旋转参数的紧凑性和奇异性问题.然而，在刚体运动中，四元数只具有表示旋转的能力[36].因此，我们使用将四元数和对偶数结合的对偶四元数[37]，它可以在一个公共框架内表示平移和旋转.每个对偶四元数有2个四元数：实部和对偶部[38].实部仅表示旋转，对偶部表示平移和旋转.在我们设计的方法中，对偶四元数由8维向量表示，在第2节将给出详细推导.

2 使用对偶四元数进行刚体变换估计

本节我们主要介绍对偶四元数进行刚体变换估计的理论保证.四元数只能表示旋转，而对偶四元数可以同时表示旋转和平移.我们从使用四元数表示旋转的有效性出发，解释对偶四元数的有效性以及为什么它可以同时表示旋转和平移.

Q=(q0,q)=q0+q1i+q2j+q3k，

(1)

其中，q0∈为实部，q=(q1,q2,q3)为虚部[39-40].另外，我们定义四元数的模：

(2)

以及共轭四元数：

(3)

(4)

对偶四元数由2个四元数Q，Qε以及对偶单元ε组成，它可以同时表示旋转和平移：

Qd=Q+εQε.

(5)

我们定义对偶四元数的共轭：

(6)

我们使用单位四元数R=(r0,r)=r0+r1i+r2j+r3k和虚四元数T=(0,t)=t1i+t2j+t3k来表示转换[42].

(7)

其中，A=t1r1+t2r2+t3r3，B=t1r0-t3r2+t2r3，C=t2r0+t3r1-t1r3，M=t3r0-t2r1+t1r2.与式(4)的旋转四元数类似，对于点P=q1i+q2j+q3k，四元数通过扩展为对偶四元数Pd=1+εP表示旋转和平移，并且可以获得变换后的点:

(8)

通过上述推导，我们可知使用对偶四元数表示刚体变换中旋转和平移是可行的，其需要8个参数，其中(r0,r1,r2,r3)表示旋转，(A,B,C,M)表示平移和旋转.再次需要强调的是，对偶四元数可以同时表示旋转和平移.本文中，对偶四元数将用于刚体变换估计阶段，即使用多维度信息融合进行特征挖掘后，使用深度神经网络拟合对偶四元数的变换参数进行配准.在后续实验中，我们验证了采用对偶四元数进行变换参数估计的有效性.

3 基于多维度信息融合的点云配准

本节我们将系统介绍本文方法的详细流程.一个点云可以被表示为一组3D点的集合{P：pi|i=1,2,…,N}⊂3，其中每个点pi表示为一个由坐标构成的3D向量.我们分别用PT和PS表示模板点云和源点云.我们的目的是寻找到一个最优的变换矩阵G∈SE(3)，使得PT和PS完美对齐.刚体在三维空间的运动由旋转R和平移T描述.简单的变换参数估计可以使用欧拉角、齐次矩阵或四元数来表示.然而，欧拉角容易出现奇异性，齐次矩阵和四元数不能同时表示旋转R和平移T.因此，我们在点云配准中使用对偶四元数进行了变换参数估计.对偶四元数的优点在于，在一个公共框架内，仅使用8个参数就可以组合表示旋转和平移.特别是，它们也可以用矩阵表示，这使它成为一种高效的计算工具.我们在第2节中描述了对偶四元数及其相关推导.为了准确获得对偶四元数的8个参数，我们设计了MIFNet，其中包含了一个特征提取网络和一个由全连接层(full-connected, FC)构成的刚体变换估计网络.其中特征提取部分可以弥补局部特征的不足，充分挖掘点云中的高维全局和低维局部信息，有效弥补了点云配准的全局特征提取阶段局部特征的缺失，为后续刚体变换估计提供准确的特征表示，以提升参数估计的精度，更多细节见3.1节.在3.2节中描述了关于本文方法的损失函数.

3.1 网络的详细架构

点云数据是高度非结构化并具有排列不变性的.目前研究者们提出了许多提取点云全局特征的方法，如PointNetLK和PCRNet，它们为获取包含几何信息的全局特征提供了一些创新性的方法.同时，它们允许将原始点云直接作为网络输入，并可以嵌入到更大规模的网络中.但是，它们没有考虑到点云提取特征过程中的局部特征，不能充分利用点云信息.为了解决现有方法中的这些问题，我们提出了MIFNet.图1显示了MIFNet的体系结构.该系统由特征提取网络和基于对偶四元数的刚体变换估计网络2部分组成.图2显示了提出的特征提取网络架构.

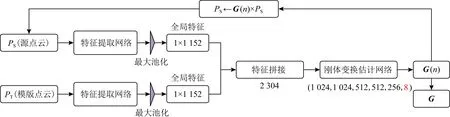
Fig. 1 Illustration of MIFNet图1 MIFNet示意图

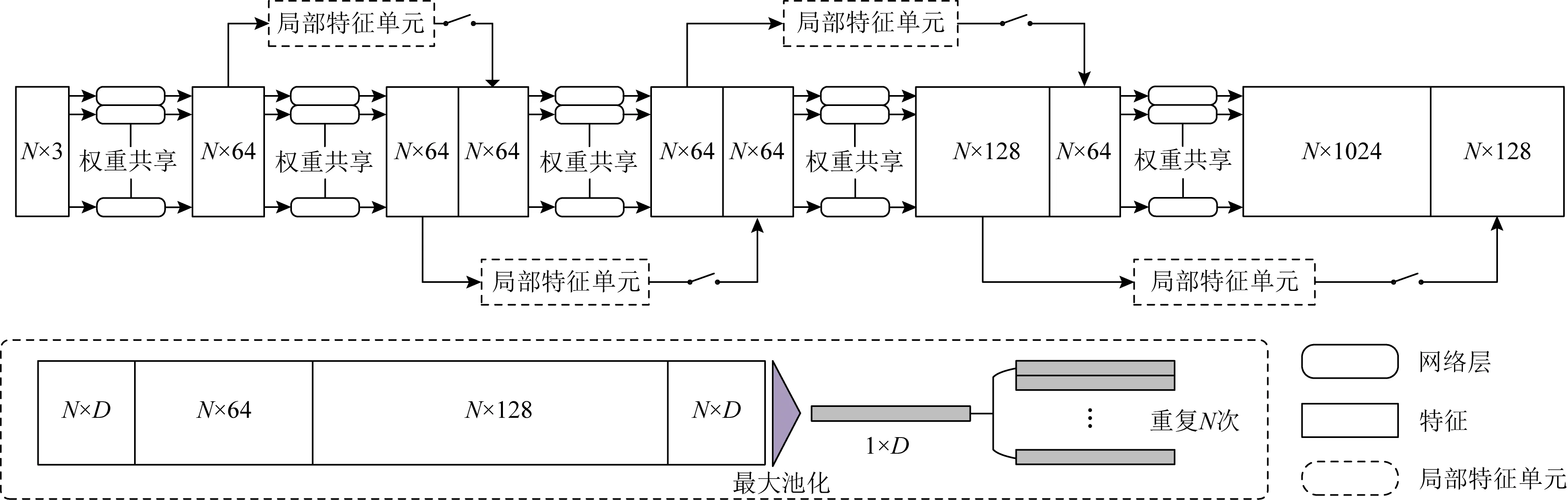
Fig. 2 Illustration of architecture of global features extraction图2 全局特征提取网络架构示意图

在特征提取网络中，我们为点云中的每个点提取特征.随着网络层数的加深，低维局部信息无法复用导致特征无法充分利用，可能使最后提取到的全局特征忽略了原始点云的某些信息.此外，为每个点进行特征提取时，点与点之间的信息相互独立，无法进行信息交互，我们为此设计了局部特征(local feature, LF)单元将低维局部特征输入到下一层.LF单元将各个维度的局部信息反馈给下一层的每个点，充分利用了各个维度的局部信息，而且每个点都会拥有其他N-1个点的特征信息.在提取高维全局特征时，相邻层之间使用LF单元会得到更多的点云低维局部信息，并且加强了信息交互，从而实现多维度信息融合.

LF单元由3个大小分别为64,128,D的多层感知器(multi-layer perceptions, MLPs)组成.输出的维数为D，与输入的维度相同.然后，利用对称的最大池化函数得到一个大小为1×D的特征向量.最后，在LF单元中，将特征向量重复N次并拼接到后续层中每个点的特征上.特征提取网络由5个MLPs组成，大小分别为64，64，64，128，1024.使用LF单元后，各层特征尺寸分别扩展到64，128，128，192，1152.如图1所示，使用特征提取网络和对称的最大池化函数提取全局特征.

提取全局特征后，将这些全局特征拼接并输入到由FC构成的刚体变换估计网络.FC层有大小为1024，1024，512，512，256的5个隐藏层和一个8维向量的输出层，该8维向量表示估计的变换矩阵G，其中n为当前迭代次数.根据第2节的分析，此8维向量对应了对偶四元数表示变换需要的8个参数(r0,r1,r2,r3,A,B,C,M).因此我们可以使用刚体变换网络学习到的8个参数进行旋转矩阵R和平移向量T表示：

R=

(9)

(10)

最后，我们使用一个迭代方案来更新PS.在第一次迭代后，我们根据R和T可以得到变换矩阵G：

(11)

在后续的迭代中，使用G对源点云进行变换，将更新后的源点云作为MIFNet的输入.经过n次迭代，结合每次迭代中估计的变换矩阵，可以得到最终估计的整体变换：

Gest=G(n)×G(n-1)×…×G(1).

(12)

3.2 优 化

针对我们的任务，我们选择了考虑对应点之间的损失的倒角距离损失：

(13)

以及从全局变换角度考虑的刚性变换的损失：

(14)

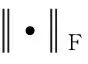
L=L1+λL2.

(15)

我们将在后续实验中讨论超参数λ的最优值，当模版点云与源点云完全配准时，L为0.

4 实 验

本节我们通过在ModelNet40数据集上评估提出方法的有效性.我们分别证明了所提出方法的准确性和对噪声的鲁棒性.我们将本方法与ICP，PointNetLK，CorsNet，DirectNet和PCRNet进行了比较.我们使用真实变换与网络预测变换之间的均方根误差(root mean squared error,RMSE)作为评价指标.需要指出的是，如果配准结果是完美的，则RMSE=0.

4.1 实验设置

在我们的工作中，使用ModelNet40数据集，共9 840个样例来训练我们的网络.ModelNet40包含40个不同对象类别，共12 000多个计算机辅助设计模型，例如飞机、椅子、人或桌子.网络训练了200代，使用10-3的学习率和0.7的指数衰减率，批量大小是32.迭代次数n=2.为了防止过多的变换信息影响点之间的对应关系，我们设置了一个比例损失因子λ来补偿这种不平衡，从而得到组合目标函数.使用Adam优化器更新网络参数.

4.2 最优的超参数λ

我们讨论了损失函数L中超参数λ的最优值.首先，我们优先说明为什么在损失函数的L2一项中添加权重项，并将权重范围的值设置得明显小于L1一项.

我们在第4.1节的基础上，对于不同的损失函数我们进行了实验，实验结果如表1所示.我们可以发现，单独使用某项损失函数时，配准效果并不如两者的组合，这是因为我们设置的损失函同时考虑了局部对应点关系以及全局变换，使得优化效果更佳.此外，我们还可以发现，单独使用L2作为损失函数的效果明显要比L1差很多，因此，我们在损失函数中为L2添加权重项，并将其设置为超参数，使其值显著小于L1，降低其对总体优化的影响.因此，我们设定在0.001 ～ 0.01范围内寻找性能最好的λ.

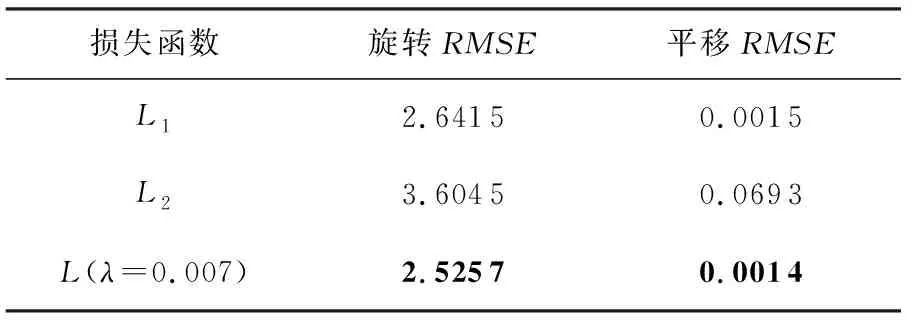
Table 1 Registration Error Using Different Loss Functions表1 使用不同损失函数的配准误差

结果如图3所示.结果表明，当λ=0.007时，平移和旋转的RMSE可以同时达到最优值.因此，后续实验均在λ=0.007的条件下进行.

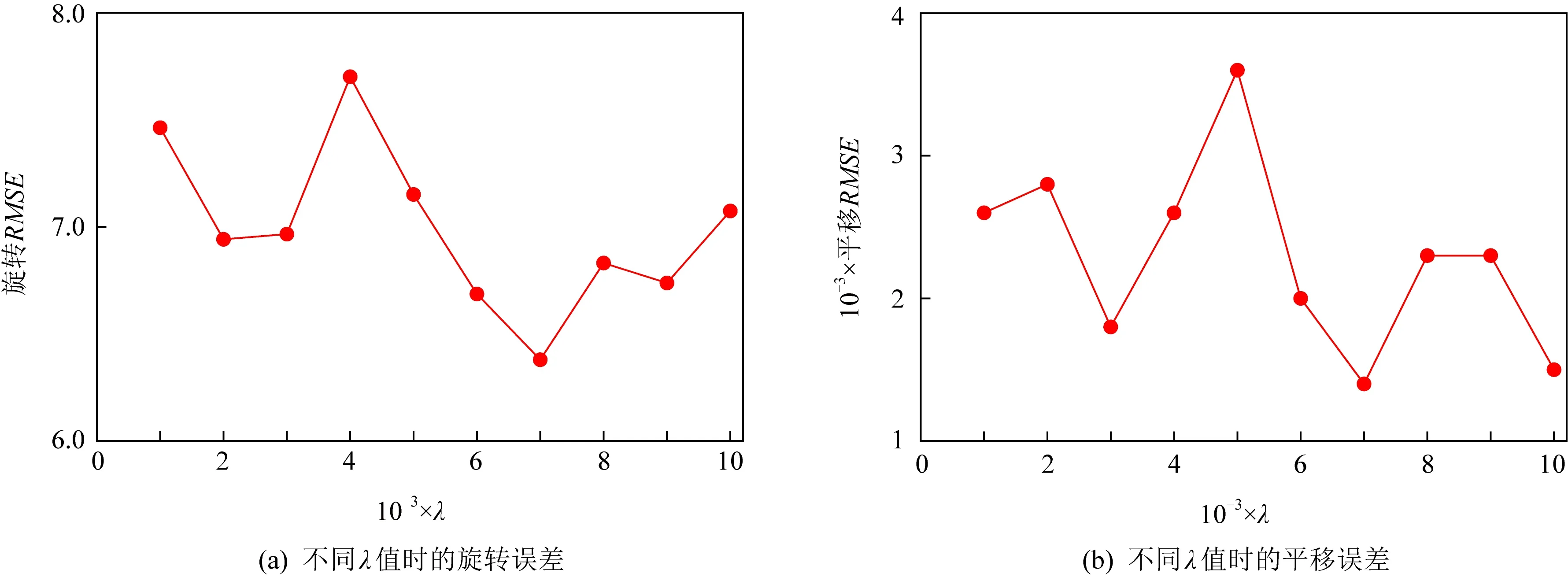
Fig. 3 Registration results with different values of λ图3 不同λ值时的配准结果

4.3 和现有方法比较

为了改进我们提出方法的性能，我们将MIFNet与ICP,PointNetLK,DirectNet,CorsNet和PCRNet进行了比较.在实验中，我们保留了所有对比方法中的实验设置.表2给出了各方法的性能评价结果.结果表明：我们所提出的网络MIFNet在达到了最高的精度.此外，我们发现，在无对应的点云配准方法中，我们的方法可以在较少的迭代下产生卓越的性能.为了更清晰地展示我们所提出方法的效果，我们选取了9个比较有代表性类别的可视化结果，如图4所示.

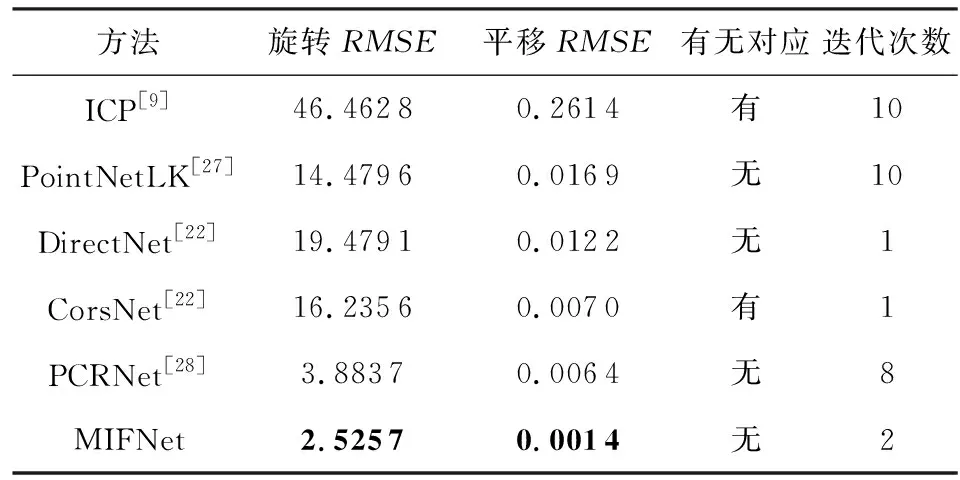
Table 2 Comparison Between the Proposed Method and the State-of-the-Art Methods表2 提出方法和先进方法的对比

Fig. 4 A part of visual registration results of representative categories on ModelNet40图4 ModelNet40部分具有代表性类别的可视化配准结果

4.4 网络泛化性研究

为了验证网络的泛化性，即对于未看见过的类别的配准效果.我们通过使用不同的类别进行训练和测试来评估所提出的网络结构.我们将ModelNet40分为2部分进行训练和测试.每个部分有20个类别，每个类别是不同的.测试部分的类别和训练部分的类别没有重合.表3给出了各方法的性能评价结果.结果表明，即使在以前从未见过的类别中，MIFNet仍然可以取得更好的性能.

Table 3 Comparison Between the Proposed Method and the State-of-the-Art Methods on Different Categories When Training and Testing表3 在不同类别上训练和测试时提出方法和先进 方法的对比

4.5 高斯噪声

为了探索我们的网络对噪声的鲁棒性，我们在源点云上进行了高斯噪声的实验.对于源点云中的每个点，使用来自高斯分布的噪声，均值为0，标准差为0.04.我们和带有噪声的ICP,PointNetLK和PCRNet方法进行比较.确保数据集具有相同的源点云和模板点云对，以便进行公平的比较.图5显示了最终结果，横轴代表使得变换估计成功的最大旋转误差(角度制)，纵轴代表实验成功的比率.在这个实验中，我们使用受试者工作特性曲线(receiver operating characteristic curve,ROC)来评估每种方法的质量，并使用ROC曲线下的面积(area under curve,AUC)作为度量标准.AUC值越高，网络的性能越好.我们观察到，MIFNet方法的AUC明显高于ICP,PCRNet和PointNetLK方法，这意味着我们的方法对高斯噪声有更强的鲁棒性.

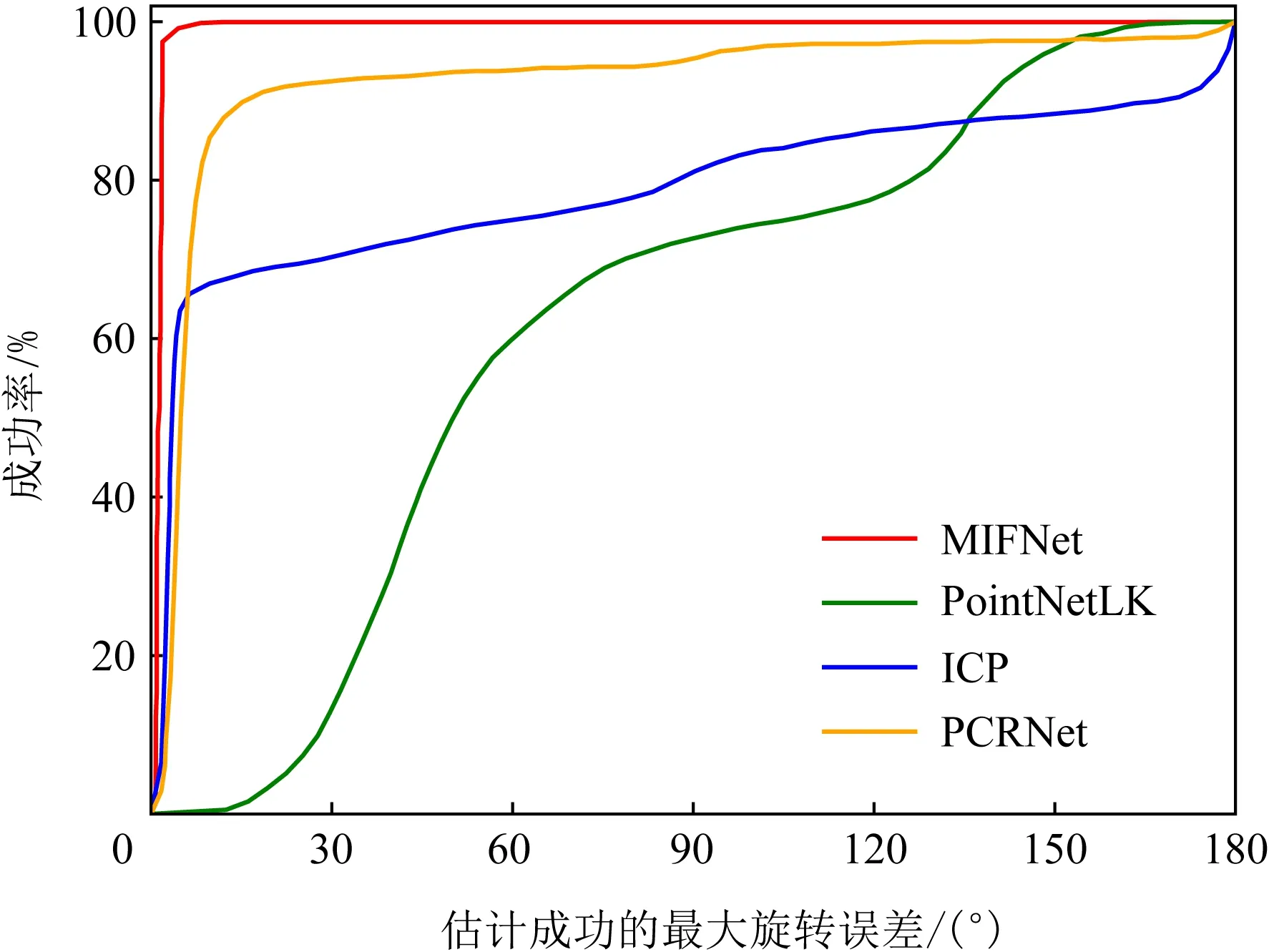
Fig. 5 Experimental results of Gaussian noise图5 高斯噪声的实验结果

4.6 消融实验

为了探索我们提出方法的有效性，我们分别对特征提取部分和使用对偶四元数进行变换参数估计部分进行了消融实验.其中，特征提取部分使用我们提出的多维度信息融合方法与PointNet进行对比，变换参数估计部分使用对偶四元数与四元数进行对比，经过不同的组合，结果如表4所示，可见，当使用多维度信息融合与对偶四元数进行配准时效果最佳，这也验证了实验的正确性和有效性.

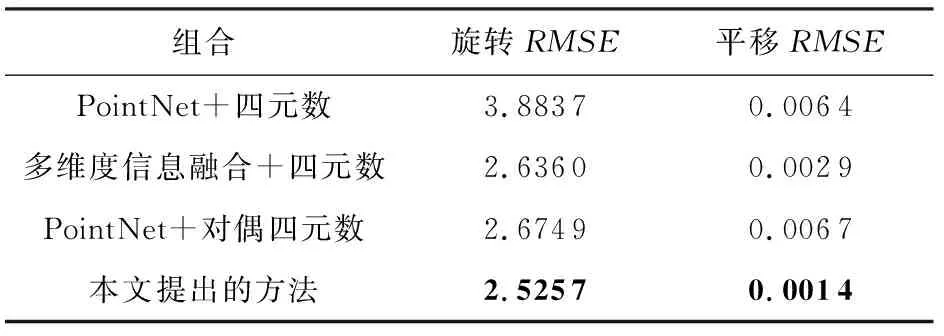
Table 4 Ablation Studies of Each Part表4 每个部分的消融实验

5 结 论

本文从定性和定量2方面验证了我们提出方法的优越性.我们在ModelNet40数据集上验证了所提出的网络——MIFNet的有效性，并比较了5种现有先进方法来说明其优越性.本文提出了一种基于多维度信息融合的特征提取网络和对偶四元数的刚体变换估计网络点云配准框架.我们的方法可以直接将点云作为输入.该网络弥补了现有大多数方法无法充分利用局部特征的不足，并使用对偶四元数估计刚性变换.与传统的点云配准方法相比，我们的方法不需要寻找点云的对应关系，并且对噪声有很强的鲁棒性.与其他无对应点云配准方法相比，该框架可通过更少次数的迭代实现更高的精度.我们认为，考虑局部特征的无对应点云配准方法是有价值的.未来的工作将涉及更多的多维度以及多尺度等网络架构，以便集成到更大的深度神经网络系统中进行点云配准任务.