面向回归任务的数值型标签噪声过滤算法
2022-08-12姜高霞王文剑
姜高霞 王文剑,2
1(山西大学计算机与信息技术学院 太原 030006)2 (计算智能与中文信息处理教育部重点实验室(山西大学) 太原 030006)
数据质量是决定机器学习模型可靠性的关键因素之一,尤其在高风险智能应用(如癌症检测、贷款分配等)中数据质量至关重要.然而数据质量在机器学习中起到的作用正在被低估,“每个人都想做模型工作,而不是数据工作”[1].监督学习是机器学习中比较成熟的学习模式,在人脸表情识别、医学诊断等领域不断取得成功应用,但都特别依赖以较高成本获得的大规模、高质量标注数据[2-4].实际中的多数数据,包括大量公开的标准数据集(如MNIST,CIFAR,ImageNet等),可能存在大量的标签噪声,QuickDraw数据的标签错误率甚至超过10%[5].诺贝尔奖得主Kahneman认为噪声是影响人类判断的黑洞,实际存在的噪声远比人们预期的要多[6].加州大学的知名专业学者都将噪声的干扰列为人工智能和机器学习领域的重要挑战之一[7].
监督学习根据输出数据类型分为分类和回归任务.标签噪声在两类任务中分别对应了类别型标签噪声(如将性别标签“男”误标为“女”)和数值型标签噪声(如将年龄标签“3”误标为“20”).通常数值型标签噪声问题更为复杂也更难解决,主要原因是数值型噪声取值范围更广、分布类型更复杂[8-10].实际中人们不知道一个数据集中是否有标签噪声,即使有噪声也不知道哪些样本有噪声、噪声有多大、噪声有多少、噪声服从什么分布等.因此解决回归任务中的数值型标签噪声问题是一项具有挑战性的任务.
对于标签噪声问题主要有2种解决思路:1)从算法层通过重构损失函数、样本加权或集成方式建立噪声鲁棒模型[11-13],这些模型并非对噪声完全鲁棒,还会在一定程度上受到噪声干扰[14],在未知噪声和强噪声情况下这些模型表现不够满意[15];2)从数据层面实施噪声过滤或纠正,也就是要将错误标签数据去除或改正[16].相比于鲁棒建模方法,噪声过滤方法只需要给出样本过滤结果,不需要对模型进行任何改动,因此噪声过滤的普适性更强、门槛更低.这类方法虽能降低数据噪声水平,但无法保证模型泛化能力,而且难以适应不同噪声环境.
针对回归任务中的数值型标签噪声问题,本文从泛化误差界视角分析了数据因素(样本量和噪声水平)对模型泛化能力的影响,并据此构建了样本过滤框架和噪声过滤算法.本文工作的主要贡献包括4个方面:
1) 修正了标签噪声环境下回归模型的泛化误差界,明确了影响模型泛化能力的关键因素,为提升模型泛化能力的样本过滤算法提供了理论指导.
2) 以降低泛化误差界为目标,提出一种关于相对噪声水平和相对样本量的可解释样本过滤框架,它可以与一般噪声估计方法结合,形成新的过滤算法.
3) 分析了噪声与覆盖区间中心和半径的单调关系,据此提出一种相对噪声估计方法,并与前面所提样本过滤框架结合设计了相对噪声过滤算法.
4) 在标准数据集和真实人脸年龄估计数据集的实验结果表明,所提算法可以有效提升数据质量和模型的泛化能力.
1 相关工作
标签噪声过滤通过去除噪声样本提升含标记数据的质量,进而提高监督学习模型的预测性能.
由于k近邻模型对标签噪声较为敏感,k近邻模型常用于检测和过滤标签噪声.其主要思想是,如果一个样本的标签与其多数近邻的标签不一致,则认为出现标签噪声.典型算法有编辑近邻(edited nearest neighbor, ENN)过滤器、全编辑近邻(all edited nearest neighbor, ANN)过滤器[17]、近邻感知(perception of nearest neighbor, PNN)过滤器[18].在回归任务中,如果模型误差超过一定阈值,则认为出现数值型标签噪声,这是一种面向回归的编辑近邻过滤算法(edited nearest neighbor for regression, RegENN)[9].
集成过滤方法利用多个分类模型产生样本预测标签,如果多数预测标签与其实际标签不一致,则认为标签存在错误应当去除[19-20].这些基模型可以采用不同类模型(如多数投票过滤),也可能是经不同子集训练过的同类模型(如迭代划分过滤).
受到特征选择的启发,文献[21]提出一种基于互信息(mutual information, MI)的噪声过滤算法.如果样本去除其近邻后特征与标签之间的互信息均发生明显的变化(超过某个阈值),则认为此样本存在标签噪声.
回归任务的标签可以通过离散化的方式将其转化为分类任务,这样就可以利用分类标签噪声过滤算法来识别回归中的数值型标签噪声.离散编辑近邻(edited nearest neighbor based on discretization, DiscENN)对数值型标签做离散化处理后采用近邻过滤来识别噪声[22].
多数噪声过滤算法虽然能够降低数据的噪声水平,但无法保证提升模型预测性能.为此文献[10]从泛化误差界视角提出一种噪声过滤的最优样本过滤框架和覆盖距离过滤(covering distance filtering, CDF)算法.此框架为降低过滤后模型的泛化误差界提供了理论保障,对指导噪声过滤具有重要意义.
上述方法中,MI,RegENN,DiscENN,CDF是面向回归任务的数值型标签噪声过滤算法.部分算法的过滤效果比较依赖阈值,而阈值通常根据经验指定,缺乏对噪声数据的自适应性.阈值设置不当容易导致过度清洗,也就是去掉大量无噪样本.虽然文献[10]给出了过滤的理论依据,但过滤目标函数中包含参数较多且形式复杂,不利于直观理解和实际应用.在这些参数中,误差界的置信度对结果影响不大,但增加了目标函数复杂度;有些模型的VC维是无穷或不可计算,在实际应用中需要根据经验指定.
2 泛化界视角下的噪声过滤框架
本节通过修正无噪条件下的学习理论得到含标签噪声情况下的泛化误差界,并据此提出含噪数据的过滤框架.
2.1 基本定义
(1)
定义1.真实经验误差.回归模型f(x)经数据D训练后基于无噪标签的真实经验误差:
(2)
定义2.实际经验误差.模型在第i个样本的实际误差ri=f(xi)-yi,基于含噪标签的实际经验误差:
(3)
2.2 泛化误差界
引理1[23-25].对于平方损失下的无噪回归任务,以下泛化误差(上)界以1-δ概率成立:
R(f,D)≤Remp(f,D)×ε(D),
(4)
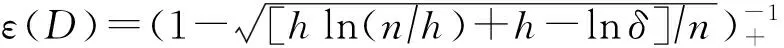
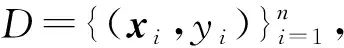
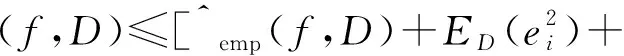
(5)
证明.含标签噪声时的真实经验误差:
2Cov(ei,ri)+2ED(ei)ED(ri)=
(6)
其中模型误差ri=f(xi)-yi,E(·)为期望函数,Cov(ei,ri)表示噪声ei与模型误差ri的协方差.
ε(D)不受标签噪声的影响.由引理1可得模型具有泛化误差(上)界:
(7)
证毕.
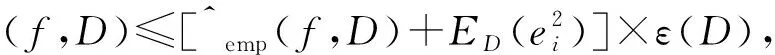
2.3 噪声过滤框架
本节利用定理1的结果确定影响泛化误差界的关键因素,并据此来构造合理的噪声过滤目标函数.
噪声过滤的目的是通过去除含噪样本来提升数据质量和模型泛化能力.将原始数据D经过过滤后的数据记为D*.为使得回归模型f(x)经数据D*训练后的泛化性能最佳,根据定理1可得误差界最低的目标:
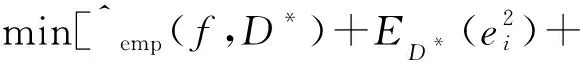
(8)
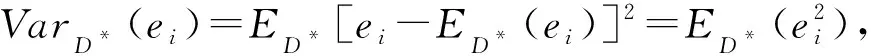
其中Var(·)和ρ(·,·)分别表示方差和相关系数.将协方差代入目标函数可得:
(9)
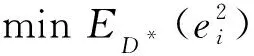
(10)
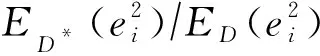
式(10)利用相对样本量和相对噪声水平来获得较低的泛化误差界,因此只需给出每个样本的噪声相对估计值即可计算出目标函数值.式(10)可以与任意的噪声相对估计方法和绝对估计方法相结合,因此它是一种适用面较广的噪声过滤框架.相比于文献[10]中的过滤框架,式(10)放弃了次要因素(误差界的置信度和模型VC维),精简了目标函数,使其可解释性更强,且其中不需要预先指定任何参数.
图1给出了噪声过滤框架的模拟结果.图中横坐标表示去噪比例γ=1-n*/n,直线表示相对样本量随γ的变化趋势,曲线表示相对噪声水平随γ的变化趋势.其中样本量设为1 000,噪声比例为25%,噪声服从正态分布N(0,0.52).由于实际中无法将所有噪声准确估计和排序,这里设定75%的噪声能够正确排序.按照噪声先大后小的顺序依次去除,重复200次后得到平均相对噪声水平曲线.
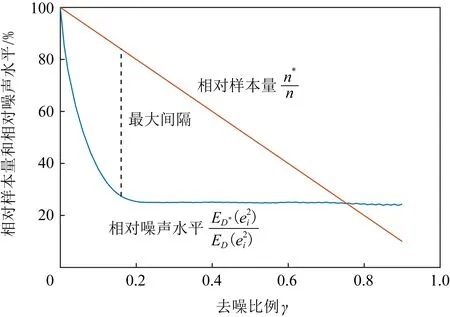
Fig. 1 Simulation of noise filtering framework图1 噪声过滤框架模拟
总体上,随着γ增大,过滤后数据集的相对样本量变少,噪声水平也变低,但噪声水平的变化一般遵从先快后慢的规律.这是因为刚开始去除较大的噪声,噪声水平下降较快;后面噪声较小后难以准确去除明显很大的噪声,故噪声水平下降缓慢;当噪声水平相差不大或噪声估计难以区分低噪声样本时,噪声水平趋于稳定.实际上,当噪声水平下降较慢时应当停止样本去除,这个位置处于两条线的最大间隔处,也就是使得式(10)达到最优的过滤结果.图1中约为γ=0.16,即应当去除16%的具有较大噪声的样本.
3 相对噪声估计和过滤算法
本节提出一种相对噪声估计方法,结合所提过滤框架得出新的过滤算法.
3.1 相对噪声估计
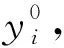
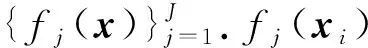
真实标签有一定概率落入模型预测值之间.令:
(11)
则其覆盖概率:
(12)
(13)
显然J越大,覆盖概率越大.但过大的J值可能使得训练子集规模过小,模型预测误差过大.实际中取J=5以平衡训练数据规模和覆盖概率,此时覆盖概率pC=0.937 5.
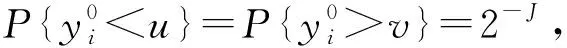
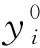
(14)
其中区间半径s=(v-u)/2,实际标签到区间中心的距离d=|yi-c|.
证明.期望绝对噪声:
(15)
不妨设yi>c,则实际标签到区间中心的距离d=yi-c>0,
(16)
由奇偶函数积分的性质可知:
(17)
(18)
因此有:
(19)
根据函数求导法则可得:
(20)
(21)
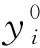
(22)
此时覆盖概率
(23)
其中,Φ(·)表示标准正态分布的分布函数.
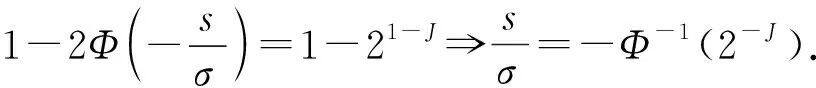
由J为正整数可知-Φ-1(2-J)>0,因此:
(24)
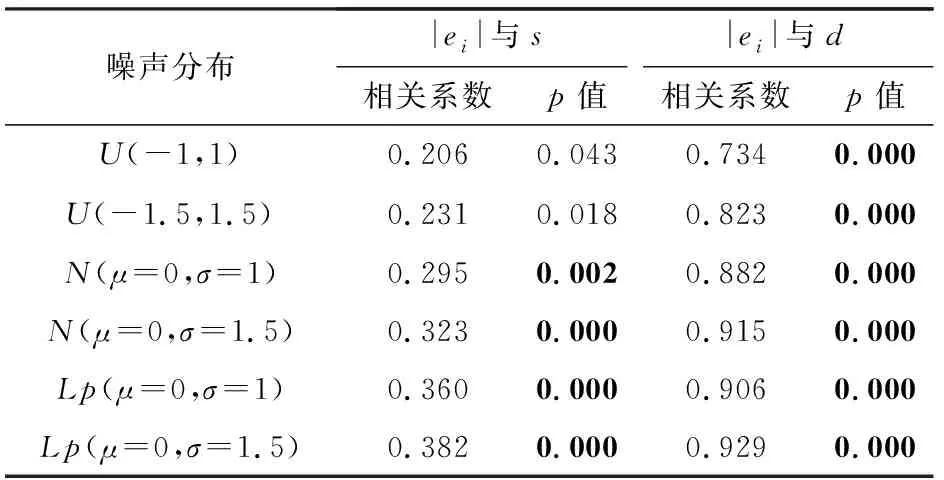
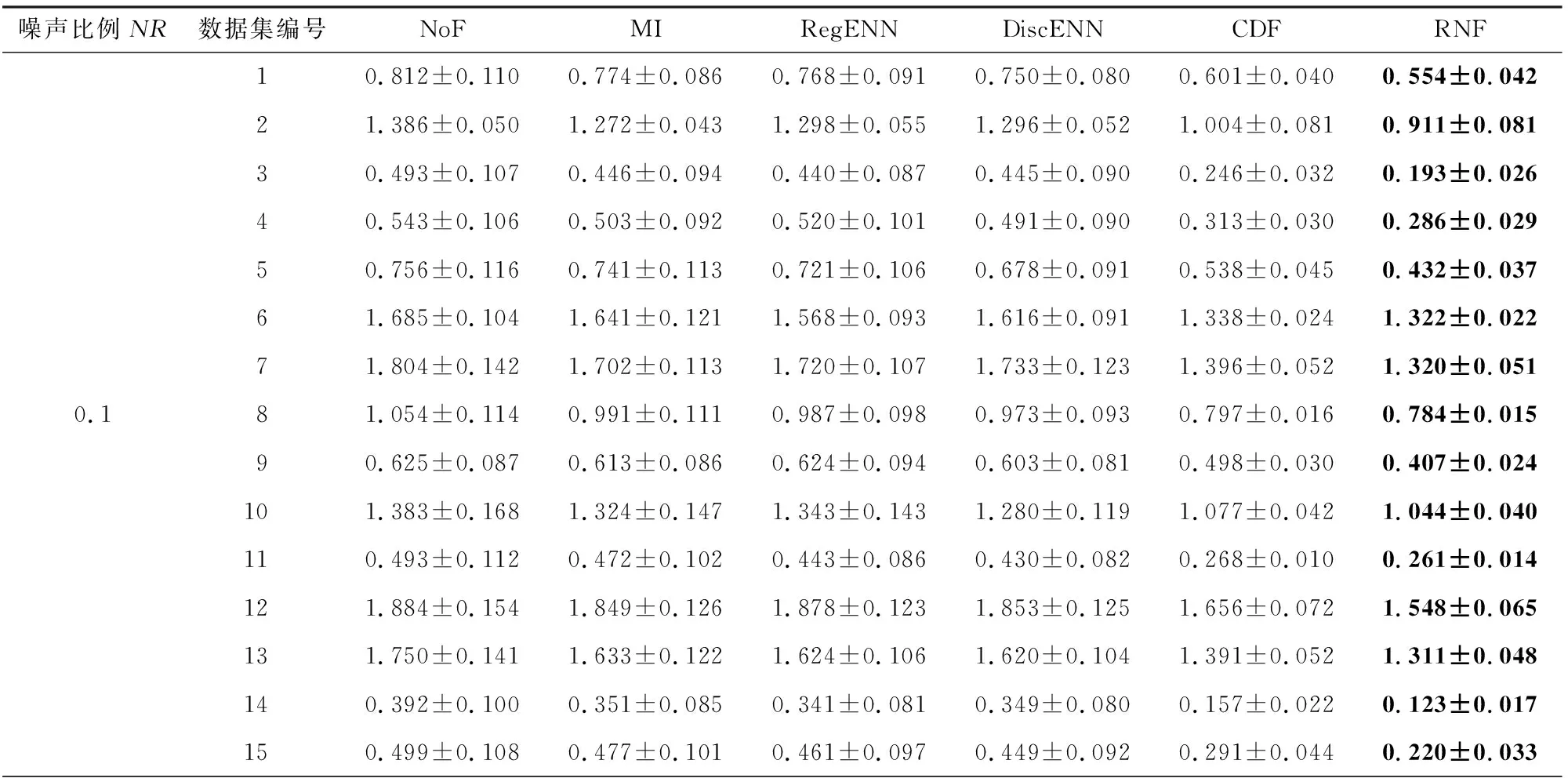
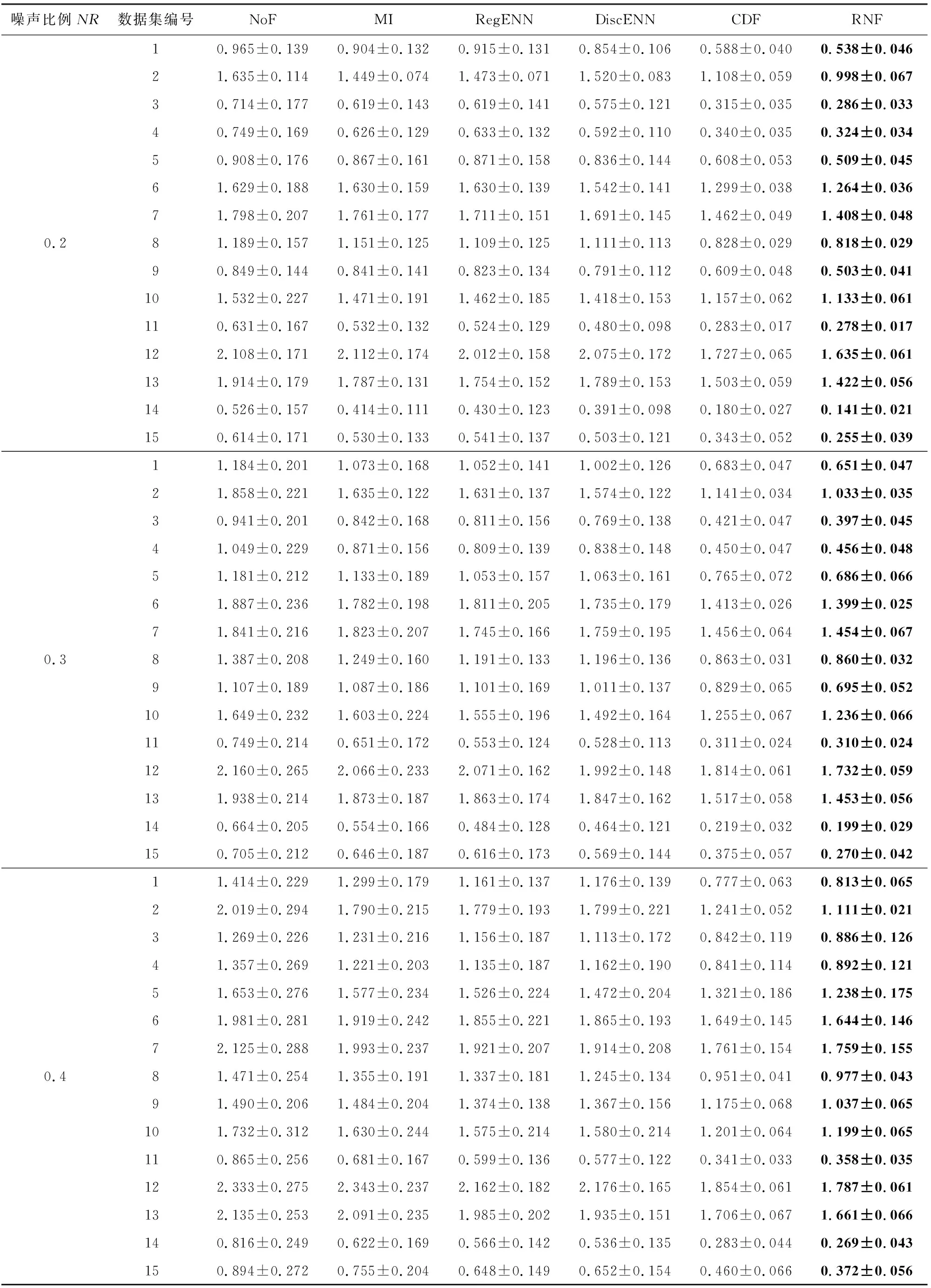
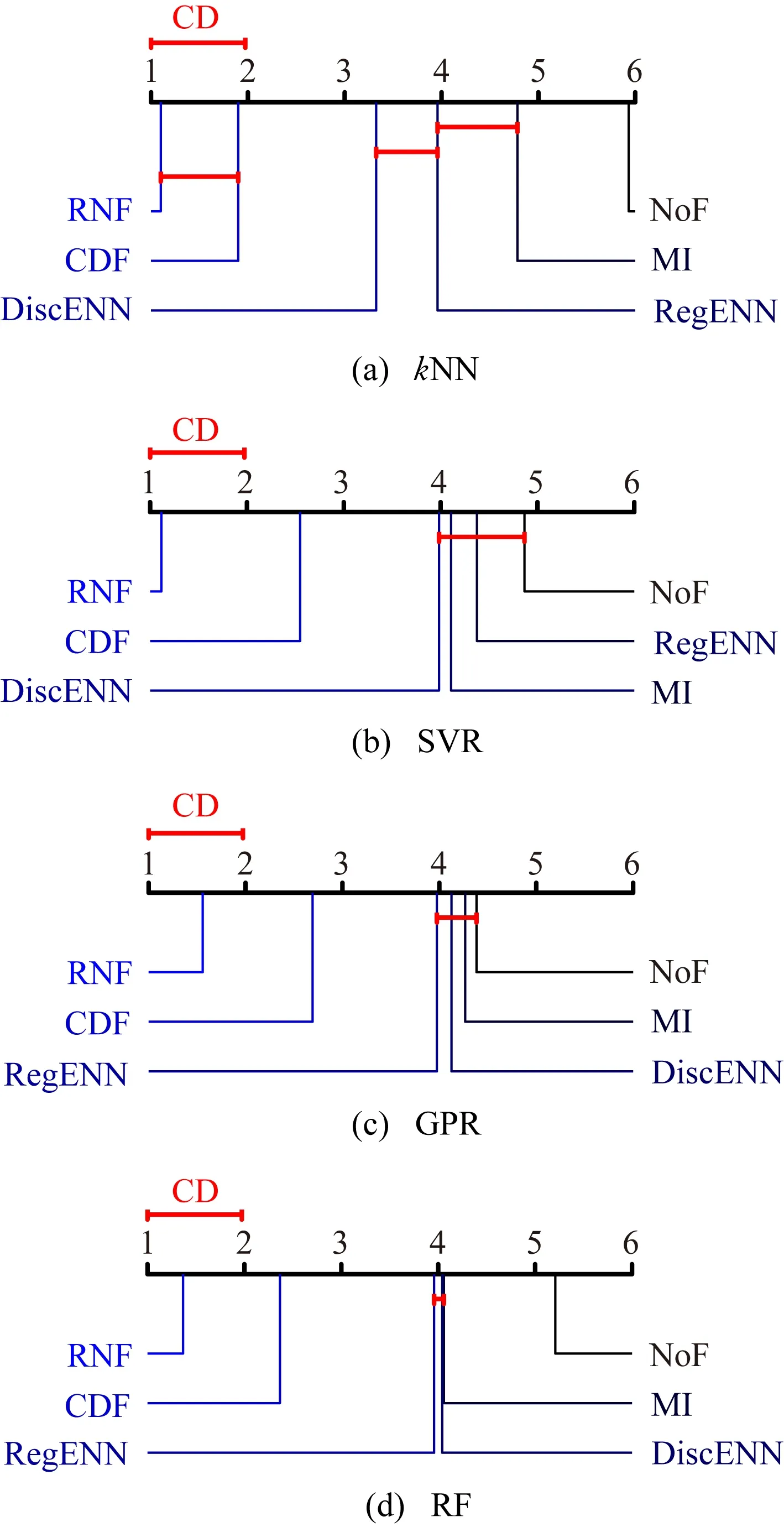
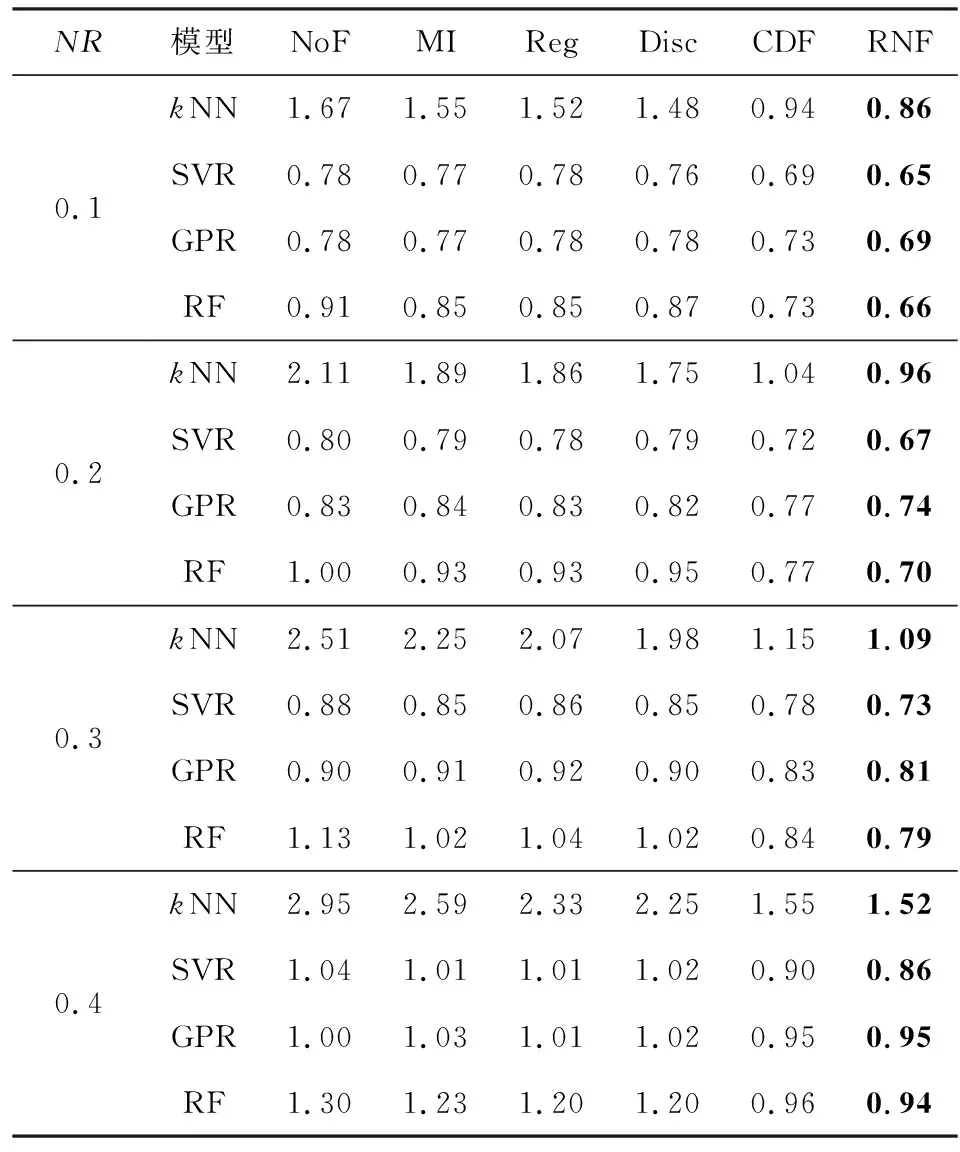
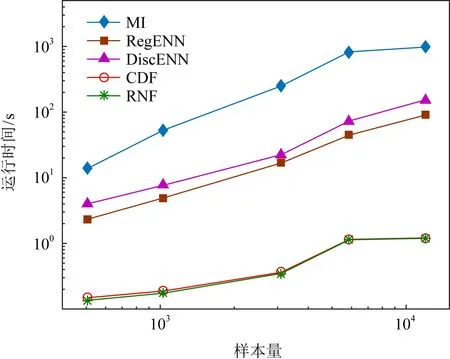
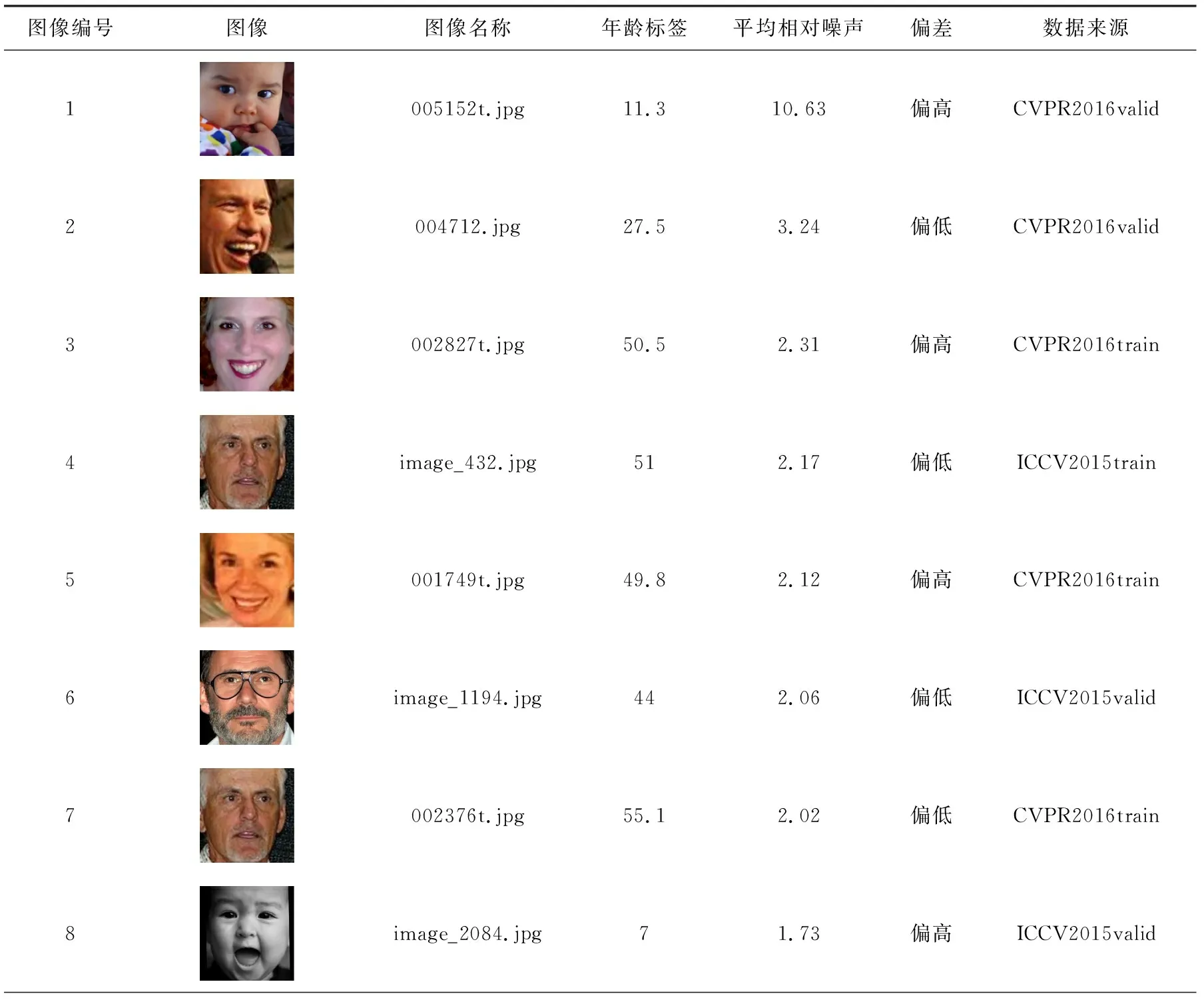
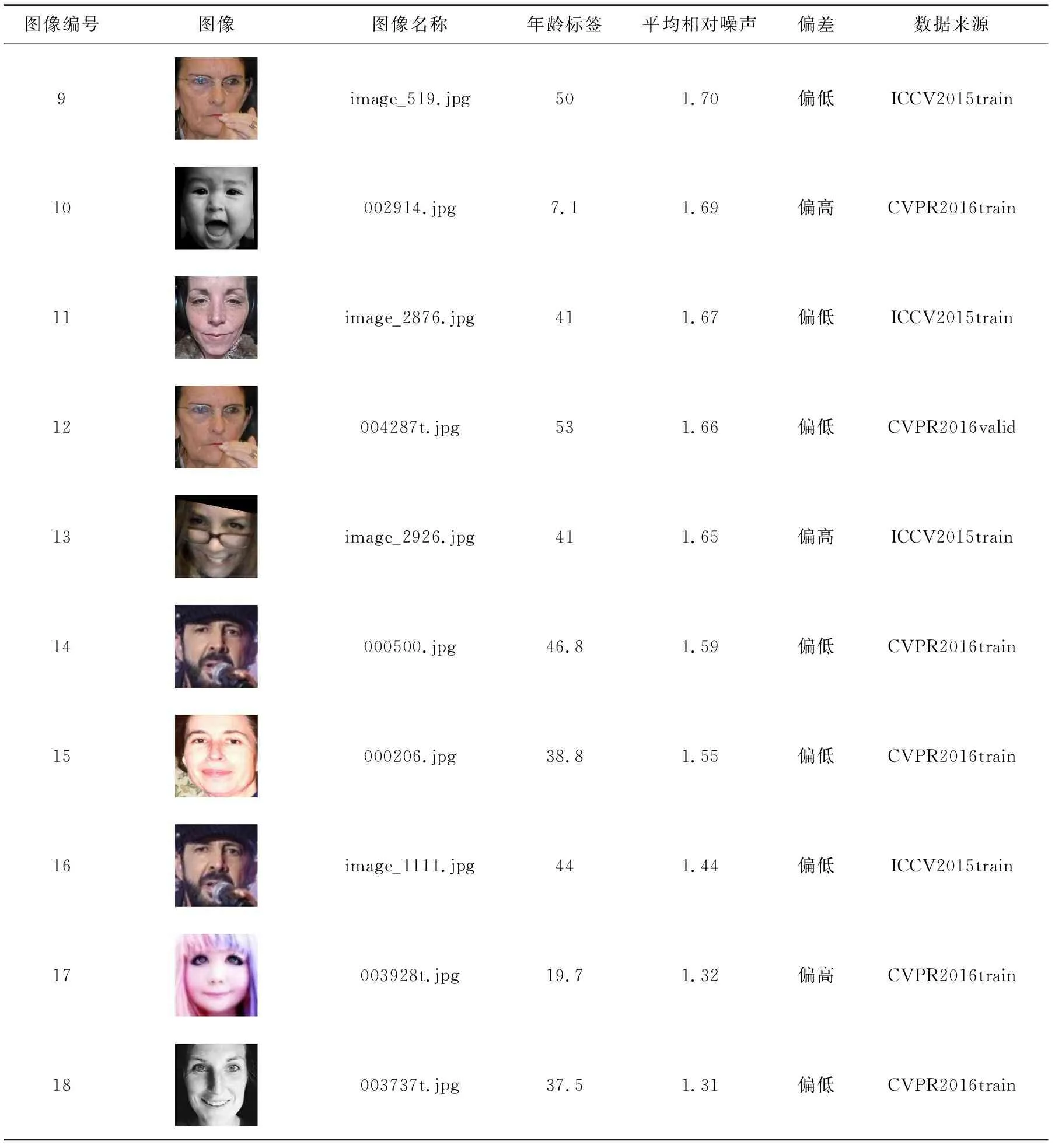
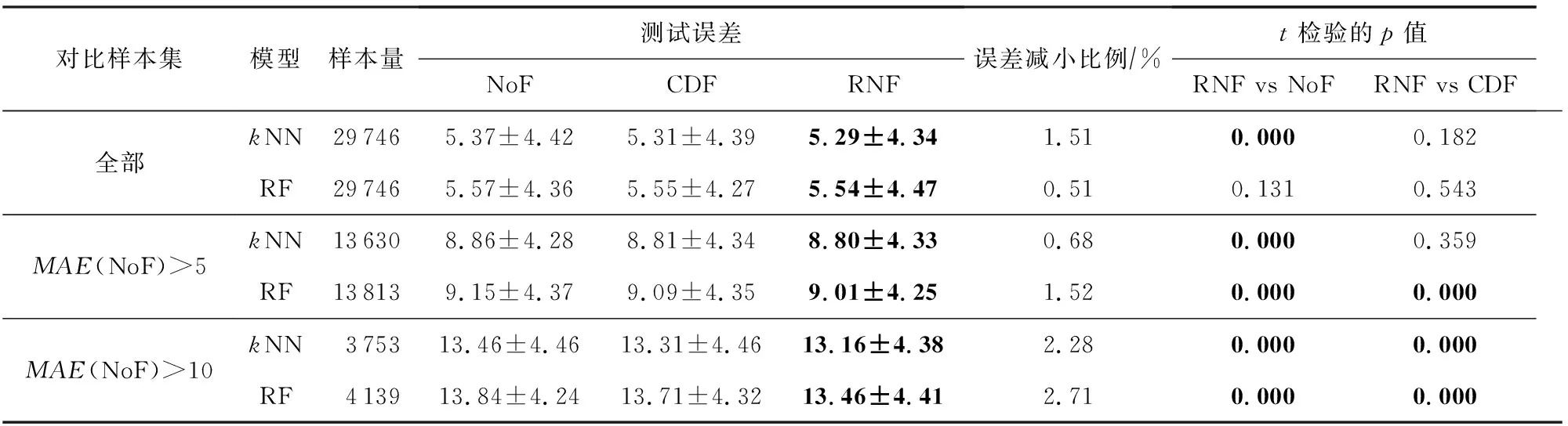
当yi 证毕. 定义4.相对噪声的定义为 (25) 其中,c和s分别为式(11)区间的中心和半径,即c=(u+v)/2,s=(v-u)/2,实际标签到区间中心的距离d=|yi-c|. 式(25)中对s做开方处理是由于其影响比d弱.公式中考虑了噪声与其关键因素的正反比关系,并未设定噪声与d和s的比例常数,因此是一种相对噪声估计方法.直观上,标签噪声越大,则yi到区间中心的距离越远(d越大);噪声越大,则分布的方差和区间半径越大.总体上相对噪声与d和s成正比. 通常大噪声样本应当先被去掉以获得较低的噪声水平.利用式(25)来估计所有标签噪声,然后逐个去除剩余子集中的最大噪声样本,并计算式(10)中的目标函数值.根据最大目标函数值即可找到最佳过滤结果. 算法1.相对噪声过滤(RNF)算法. 输出:过滤后数据集D*. ① 将数据集D随机划分为5个子集,然后用每个子集数据对回归模型f(x)进行训练,并在全部数据上进行预测; ② 根据式(11)计算覆盖区间[u,v],并用式(25)计算噪声估计值; ③ 将数据按照噪声从大到小顺序排列得到D′; ④ fort=0 ton-1 ⑥ end for 算法1在有限集合中求解固定的优化目标函数,因此一定存在最优解.实际中采用3近邻回归作为基模型.算法1中模型训练和预测的时间复杂度为O(nlogn),其余部分均为线性时间复杂度,因此算法总时间复杂度为T(RNF)=O(nlogn).如果基模型采用其他模型,则算法总时间复杂度与基模型复杂度相同. 本节首先介绍了过滤算法在标准数据集的实验框架、理论结果验证、实验结果与分析,然后在真实人脸年龄估计数据上做了标签噪声检测和泛化性能分析. 实验中首先将原始标准回归数据集随机划分为训练集和测试集,两者的样本比例为7∶3;然后随机在训练集的部分输出标签上添加人工噪声,并用各种噪声过滤算法来识别噪声和过滤样本;最后将回归模型在过滤后的数据集上进行训练,并在测试集上测试其泛化能力.实验中每轮数据划分、加噪声、过滤和预测环节均重复5次以获得稳定结果. 表1列出了实验中使用的15个标准回归数据集[26-27].数据的数值型特征均被归一化到区间[-1,1]. Table 1 Dataset Information表1 数据集信息 实验中包括8种数值型标签噪声,分别服从均匀分布U(-1,1)、均匀分布U(-1.5,1.5)、高斯分布N(μ=0,σ=1)、高斯分布N(μ=0,σ=1.5)、拉普拉斯分布Lp(μ=0,σ=1)、拉普拉斯分布Lp(μ=0,σ=1.5)、高斯混合分布N(μ=1,σ=0.3)+N(μ=-1,σ=0.3)、高斯混合分布N(μ=1,σ=0.1)+N(μ=-1.2,σ=0.5).最后2个混合分布中单个高斯分布噪声各占50%.噪声比例NR=0.1,0.2,0.3,0.4. 对比过滤算法包括基于互信息(MI,阈值为0.05,近邻数为9)的过滤[21]、回归近邻过滤(RegENN,阈值为5,近邻数为9)[9]、离散近邻过滤(DiscENN,近邻数为9)[22]、覆盖距离过滤(CDF,子集数为5)[10].此外,所提相对噪声过滤算法(RNF)还与未过滤(NoF)数据做了对比分析. 测试模型包括k近邻回归模型(kNN)、支持向量回归模型(SVR)、高斯过程回归(GPR)和随机森林(RF).模型在测试集上的泛化能力采用均方误差(mean square error,MSE)来度量: (26) 图1噪声过滤框架模拟结果显示,当相对样本量和相对噪声水平具有最大间隔时,式(10)取得最优解,此时的去噪比例较为合适,能够使模型获得较好的泛化能力.为验证此结论,在2个数据集上人工添加2类噪声,并在不同去噪比例下测试了模型的预测误差.具体设置为:1)对表1中第7个数据训练集30%的标签添加服从均匀分布U(-1.5,1.5)的噪声;2)对表1中第9个数据训练集30%的标签添加服从高斯分布N(μ=0,σ=1)的噪声.2种情况下均设置去噪比例γ=0∶0.02∶0.5对数据进行过滤,然后使用SVR,GPR和RF模型进行训练(kNN的测试误差较大),并在无噪测试集上测试模型误差. 图2显示了2种设置下模型测试误差(MSE)在不同去噪比例下的变化趋势.各模型最低测试误差采用实心圆点标出.目标函数曲线对应右侧坐标轴,在目标函数最大值(即相对样本量与相对噪声水平的最大间隔)处用竖虚线标出.图2(a)中,GPR模型在目标函数最大值处具有最小测试误差,其余2个模型在目标函数最大值处的误差非常接近最小测试误差.图2(b)中,3个模型在目标函数最大值附近具有最小测试误差.由此可见,模型最小测试误差下的去噪比例通常位于目标函数最大值附近.根据目标函数最大值来确定去噪比例,能够使模型获得最低或较低的测试误差,实验证实了所提框架的有效性. Fig. 2 Model test errors under different denoising ratios图2 不同去噪比例下的模型测试误差 定理2表明期望噪声与d和s均成正比,其中覆盖区间半径s=(v-u)/2,实际标签到覆盖区间中心的距离d=|yi-c|.为验证此结论,在表1所有数据上添加6种人工噪声,并构造覆盖区间.根据绝对噪声|ei|和区间特征s,d可以分别计算出它们的Pearson相关系数及其相关性检验的p值.相关系数和p值在所有数据上的平均值在表2中列出,其中p值越小表明相关性越显著. Table 2 Correlations Between Noise and the Characteristics of Covering Interval表2 噪声与覆盖区间特征的相关性 由表2可见,所有噪声情况下2组相关性检验的p值均<0.05且相关系数为正值,表明|ei|与s,d均显著正相关;|ei|与d的相关系数明显大于|ei|与s的相关系数,表明前者的相关性更强;从噪声分布来看,拉普拉斯分布噪声所对应的相关系数最大,均匀分布噪声的相关系数较小.表2的实验结果表明定理2所表达的正反比关系在实际中是成立的. 表3列出了不同噪声比例下各数据集上不同过滤算法的测试误差结果.通常噪声比例越大,测试误差也越大.当噪声水平较低(NR=0.1,0.2)时,所提RNF过滤算法能够使得模型的测试误差最小,且有明显优势;当噪声水平较高(NR=0.3,0.4)时,RNF算法在大多数数据上取得了最小测试误差. Table 3 Average Test Error ±Standard Deviation of Four Models with Different Noise Ratios表3 不同噪声比例下4种模型的平均测试误差±标准差 续表3 图3给出各模型测试误差的临界差异图(critical difference, CD).CD图不仅能给出不同算法的排名,还能显示算法之间的差异是否显著.图3中算法排名越小表示算法对应的测试误差越小;算法平均排名之间的距离不超过CD值时使用横线连接,表示算法之间差异不显著.图3中算法的平均排名是基于15个数据集和8种噪声水平的模型测试误差. Fig. 3 CD diagram of each regression model error图3 各回归模型误差CD图 由图3可见,所提RNF算法在各个模型上都取得了最小测试误差.在kNN模型中,RNF与CDF算法无显著性差异;在其他模型中,RNF比其他算法均有显著性优势.已有过滤算法中,CDF表现最佳,RegENN,DiscENN和MI无明显差异.所有过滤算法均比未过滤数据(NoF)效果更好,即过滤能够提升模型泛化能力,所提RNF算法的提升效果最明显. 表4列出了不同噪声比例下各模型平均测试误差.总体上噪声比例越大,测试误差也越大.所提RNF算法的测试误差最小.同时注意到,当噪声比例较低时,RNF的测试误差明显小于其他算法的误差;当噪声比例较大(NR=0.4)时,RNF的测试误差略微优于CDF算法.总之,在低噪声比例情况下RNF的优势更加明显. Table 4 Average Test Error of Each Model表4 各模型平均测试误差 图4显示了各个过滤算法在5个不同数据规模上的过滤运行时间.其中MI算法运行时间最长;RegENN和DiscENN运行时间略短;CDF和RNF的运行时间最短,而且比其他算法快至少一个数量级.在小规模数据上,RNF的效率比CDF略高,两者一般相差不大. Fig. 4 Runtime of filtering algorithms图4 过滤算法的运行时间 人脸年龄估计是一个具有挑战性的监督学习问题,ICCV和CVPR等计算机视觉顶会在竞赛任务中曾公开过人脸图像和年龄标注数据[28-29].每个图像的年龄标签是多个标记者所给年龄估计的均值,这些数据中存在部分标记与人脸图像不匹配的情况.通过RNF噪声过滤可以找到这些标签噪声数据,进而提升模型预测性能. 原始数据来自ICCV 2015和CVPR 2016[28-29],共有18 424张图像和对应年龄标签,其中2个数据子集中存在一些重复图像,每个图像通过左右翻转做了增强.图像特征采用经典的VGG16深度网络提取特征.重复执行5次RNF得到平均年龄标签噪声估计结果,表5列出了平均相对噪声排名前60的部分年龄标签噪声,图像按照相对噪声从大到小排列.表5中部分图像相同(如编号为4,7的图像),但它们所属子集不同,年龄标签也不同. Table 5 Age Label Noises Recognized by Relative Noise表5 根据相对噪声识别的年龄标签噪声 续表5 表5中既有年龄标签偏高的情况(如编号为1,5,8的图像),也有年龄标签偏低的情况(如编号为4,6,18的图像).在因特尔8核3.6 GHz处理器8 GB内存的单机上进行实验,每轮RNF过滤的时间不超过10 s.可见RNF过滤算法能够快速准确地找到标签噪声. 经RNF过滤后的数据集大约包括86%的原始样本,回归模型在过滤后的数据集上训练后,在另一个wiki年龄数据[30]上进行测试.表6中列出了误差较小的k近邻和随机森林模型的测试结果.年龄测试误差采用平均绝对误差(mean absolute error,MAE)度量. Table 6 Comparison of Test Errors with Various Filters表6 各种过滤算法的测试误差比较 表6中对比了2个模型经未过滤原始数据(NoF)、CDF和RNF过滤数据训练后的测试误差.对比的测试样本集包括wiki全部有效年龄在0~80岁样本集、不过滤情况下测试误差大于5和10的样本集.结果表明,与不过滤NoF原始数据相比,RNF在所有情况下都能够降低模型测试误差,在多数情况下能显著降低测试误差(t检验的p<0.05).与CDF过滤算法相比,RNF在wiki全部样本上与其无显著差异,在大噪声样本MAE>10上有明显优势. 总体上,RNF过滤算法在人脸年龄数据上检测出许多标签噪声数据,能够有效提升数据质量和模型预测性能. 数值型标签噪声问题给回归任务带来严峻挑战.噪声过滤可以有效识别噪声数据,但缺乏模型泛化能力提升的理论保障,实际中还存在过度清洗、自适应差、依赖参数设置等问题.本文根据无噪回归任务中的学习理论给出了面向数值型标签噪声数据的泛化误差界,从而明确了影响模型泛化能力的关键数据因素(数据量和噪声水平).在此基础上提出一种可解释的噪声过滤框架,其目标是以较小的样本去除代价最大程度地降低噪声水平.此框架不仅适用于普通噪声估计方法,也适用于相对噪声估计,只需知道噪声之间的比值关系即可. 针对噪声估计问题,从理论上分析了噪声与覆盖区间关键指标之间的变化趋势,进而构建了相对噪声估计方法.此方法与所提框架结合形成了RNF过滤算法.在标准数据集和真实人脸年龄估计数据上均验证了算法的有效性.所提框架和相对噪声估计方法均有理论支撑,可以确保算法取得良好的过滤效果.实验结果证实了RNF算法在不同噪声分布、不同噪声比例、不同数据集、不同回归模型等复杂情况下具有较好的适应性. 所提过滤框架可用于解决其他过滤算法的超参数优化和适应性问题;所提噪声估计和过滤算法为有序回归或分类任务中的标签噪声问题提供了新思路.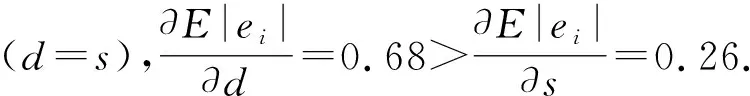
3.2 相对噪声过滤
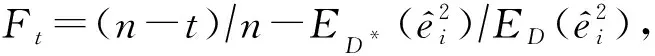
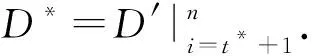
4 实验结果及分析
4.1 实验框架
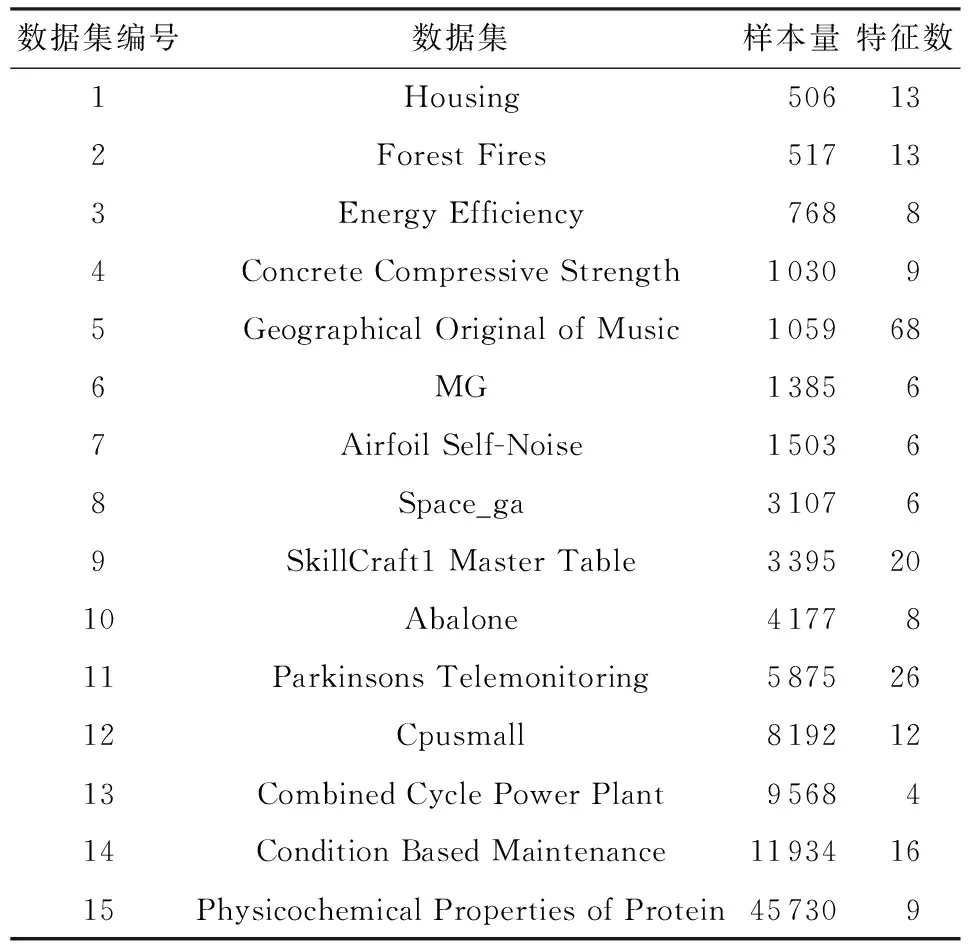
4.2 理论结果验证
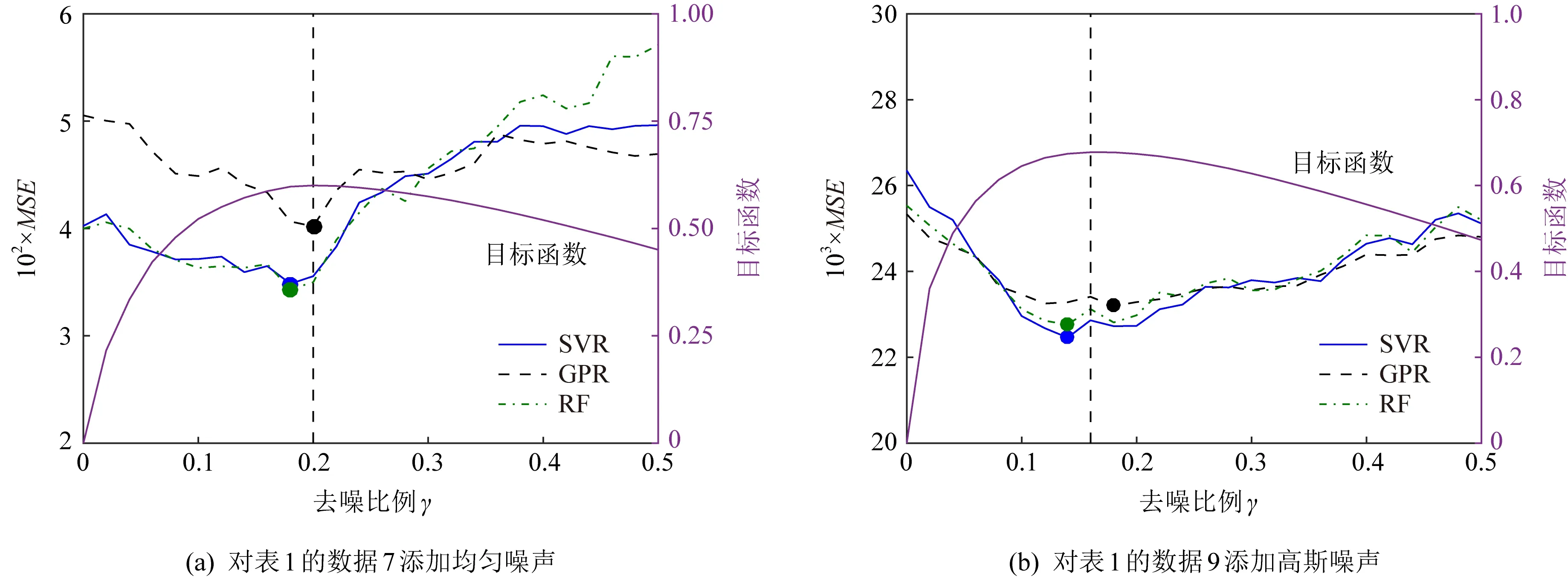
4.3 实验结果与分析
4.4 年龄标签噪声过滤
5 结 论
