基于0-1规划下企业原材料订购与运输的量化关系研究

姚成成

(湘潭大学，湖南 湘潭 411105)

1 问题一：量化分析供应商的供应特征

1.1 问题重述

量化分析402家供应商的供货情况，建立供应商对保障该企业正常生产重要程度的数学模型，进而确定出50家最重要的供应商。

1.2 问题分析

解决该问题的思路为：确定评价指标体系，并通过熵权法对各指标进行客观赋权；利用TOPSISF方法计算各供应商的评分，得到供应商的相对重要程度。

考虑到供货量对于保障企业生产至关重要，计算各供应商近5年的总供货量，确定供货量比重较大的部分供应商。针对这部分供应商，建立综合评价模型，对其进行综合评价。首先，确定对其进行量化分析的评价指标，分别为供应商供货量、企业订货量与供应商供货量之间的偏离程度、供应商供货量的变异程度。其次，通过熵权法确定各指标对应的权重。最后，对于多属性决策的评价问题，采用理想解法(TOPSIS)确定各供应商的重要程度。

1.3 模型建立

(1)初步筛选。通过Excel累加求和，确定各供应商近5年的供货总量。具体计算公式如下：

式中，表示各供应商近5年的供货总量，表示供应商在第周的供货量。

筛选出比重较大的前60家，对其进行综合评价。

(2)供应商的综合评价。针对筛选过后的60家供应商，定义供应商供货总量、订货量与供货量之间的差异程度、供货量的变异程度三个评价指标，利用熵权法确定指标的权值，建立TOPSIS综合评价模型。

①构造原始矩阵。企业订货量与供应商供货量之间的差异程度可以表示为：

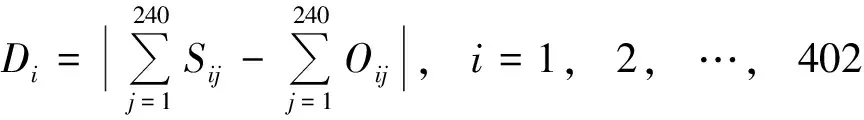
式中，表示订货量与供货量之间的偏离程度，表示供应商在第周的供货量，表示企业第周在供应商的订购量。

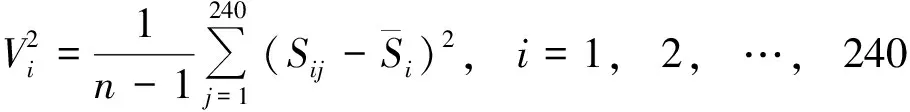
构造根据供货总量筛选出的60家供应商的原始决策矩阵=()。

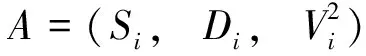
②熵权法对指标赋权。熵权法是一种客观的赋权方法,可以最大限度地避免主观赋权对供应商供应特征量化的影响，根据各指标的变异程度，利用信息熵得出较为客观的权重，变异程度越高对应的权值越高。

计算第个供应商关于第个指标所占的比重，将其看作计算熵值时的概率:

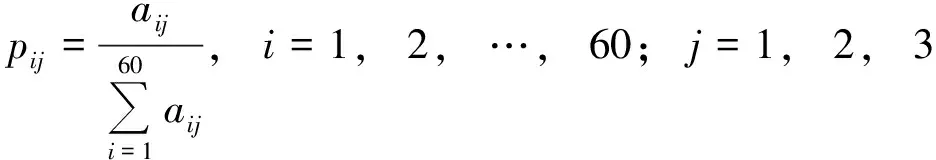
计算第项供应商供应特征指标的信息熵，并计算其对应的变异系数即信息效用值。信息熵越大，则代表供应商供应特征指标所反映的信息越少。

=1-,=1, 2, 3

归一化计算每个供应商供应特征指标的权重:

求解得到3个指标的权重如表1所示。

表1 指标赋权值

③TOPSIS方法计算各供应商评分。TOPSIS方法能够充分利用样本数据，对各供应商进行排序。其基本思想是构造评价供应商供应特征的各指标的最优组合方案和最劣组合方案，然后计算每个供应商分别与最优组合方案和最劣组合方案的距离，得到其与正理想解的贴近程度和与负理想解的远离程度，对各供应商进行排序。

Step2：对正向化处理后的矩阵进行标准化处理，消除各指标不同指标量纲的影响。

Step3：根据熵权法确定的权重得到加权决策矩阵。

Step4：确定各指标的最优组合方案和最劣组合方案即正理想解和负理想解。

Step5：计算各供应商对应的指标值与最优、最劣组合方案的距离。

Step6：对各供应商进行排序。

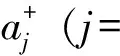
对正向化处理后的矩阵进行标准化处理，记为=()，其中：

根据熵权法计算的指标权重，构造加权决策矩阵=()，其中：

=×

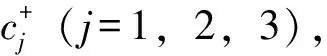
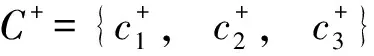
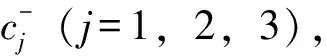
该向量代表最劣组合方案。

计算各供应商与最优组合方案和最劣组合方案之间的距离：

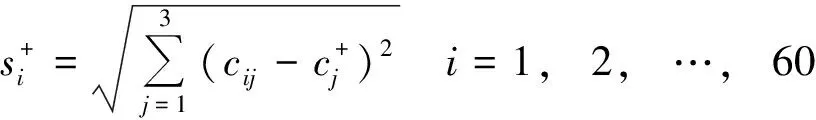
计算各供应商的得分，计算公式为：

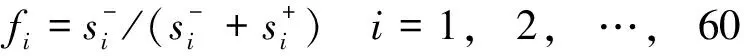
对各供应商得分按优劣进行排序。

1.4 求解结果

最终保障企业生产的50家最重要的供应商如表2所示。

表2 对该企业最重要的50家供应商

从上到下、从左到右，得分递减，重要程度下降。

2 问题二：供应商数量最少的情况下，未来24周的订购及转运方案

2.1 问题重述

确定为满足生产需求至少选择的供应商数量，并制定出未来24周最经济的订购方案，在此基础上确定损耗最小的转运方案，并对方案的效果进行分析。

2.2 问题分析

该问题可从以下三个步骤解决：通过时间序列分析预测未来24周供应商的供货量以及转运商的转运损耗率；企业对供应商提供的原材料全部收购，建立订购优化模型并求解；一家供应商原材料由一家转运商运输，建立转运的0-1规划模型。

在第一问50家供应商的基础上，根据近5年供应商的供货量以及转运商的转运损耗率，以24周为一个周期，利用时间序列分析法对其未来24周内的变化情况进行预测。将供货量转化为企业的产量，企业每周的产能为2.82万立方米。

使用0-1变量表示是否订购该供应商，以企业的原材料库存量不低于两周生产需求为条件，以供应商数量尽可能少为目标函数建立订购方案优化模型。求解优化模型确定订购方案，订购方案可确定其相应的运输量。将对各转运商未来24周损耗率的预测值作为其损耗率，以转运商运输的最大总量以及一个供应商的货物由一个转运商运输为约束条件，建立转运总损耗量最小的0-1规划模型。

2.3 模型建立

(1)订购模型。优化的目标是每周订购时供应商的数量尽可能的少。假设目前剩余原材料为28200，仅满足未来一周的生产。保证企业的正常生产运营，即保证原材料的剩余量要满足企业未来两周的生产，库存量不少于56400万立方米。

式中，表示在第周是否订购供应商，代表供应商在未来第周的供货量，表示在第周的剩余量。

(2)转运模型。优化的目标是使转运的损耗最少。经过订购量的数据处理后，一家供应商的原材料可保证最多由一家转运商运输。转运商每周所运输的供货量不高于6000立方米。可建立下列模型求解每周原材料的转运方案。

式中，表示转运商是否转运供应商的货物，代表在供应商的订购量，代表转运商的损耗率。

3 问题三：多采购A类少采购C类的情况下，24周的订购及转运方案

3.1 问题重述

为压缩生产成本，计划多采购A类和少采购C类原材料，同时转运商的损耗率尽量小。请制定新的订购及转运方案，并分析实施的效果。

3.2 问题分析

结合问题二，为降低生产成本，以各成本相对都较优的A类原材料采购所占比重最大为目标函数，以原材料存储量满足未来两周生产为约束条件，建立优化模型。结合问题二，建立以总损耗量最小为目标，以转运商运输的最大总量以及一个供应商的货物由一个转运商运输为约束条件，建立0-1规划模型。

3.3 模型建立

(1)订购模型。优化的目标是使企业A类原材料的订购量尽可能多，C类原材料订购量尽可能少，即A类原材料与C类原材料的差值最大。从402家供应商中订购。约束条件为满足两周的生产。

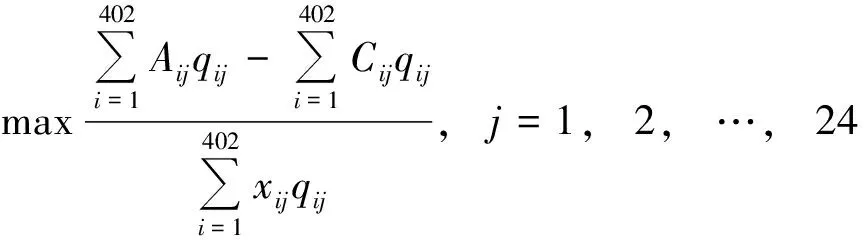
式中，表示是否在第周订购供应A类原材料的供应商的货物，表示是否在第周订购供应C类原材料的供应商的货物，表示是否在第周订购供应商的货物，代表供应商在未来第周的供货量，表示在第周的剩余量。

(2)转运模型。

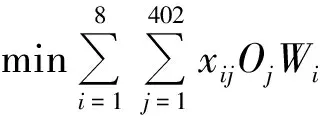
式中，x表示转运商i是否转运供应商j的货物，O代表在供应商j的订购量，W代表转运商j的损耗率。

4 模型的评价

优点：第一，归一化处理数据，分析多条件对企业供应重要性的影响，直观有效，符合实际；第二，应用线性规划模型使得文章中许多问题的求解过程十分简便，而且线性规划的理论和体系相对完备，在企业生产中求解也令人信服；第三，在对供应商评价时使用熵权法确定各指标的权值，具有客观性，可以更好地解释结果。缺点：第一，由于线性规划只能处理线性关系的情形，所以对于数据的准确性要求高，而且计算量大，最终结果可能达不到最优解；第二，因数据集过大，通过计算机仿真模拟的随机性过大，对规划模型求解的效果不好。