基于雷达软件安全的C程序到形式模型的转换方法

臧伟旺，朱健

（南京电子技术研究所，江苏 南京 210039）

0 引 言

随着雷达系统不断发展，以及结构工艺的优化提高，对雷达软件设计提出了更高的要求，其中，软件的安全性与可靠性尤为重要，影响着整个雷达系统的行为是否符合预期以及性能的高低。传统的测试仿真方法可以有效提高软件的可靠性，但无法遍历所有的执行路径，从而不能证明一个软件没有漏洞。因此，需要引入形式化方法来保证软件的安全性。

形式化方法是一种基于数理逻辑的软硬件设计方法，也是目前安全关键软件系统的一种严格的验证技术。通过形式化逻辑的方式来表示合约代码，并加以严格地推理证明。这个过程依赖于数学逻辑推理的严密性，保证100%覆盖到代码的运行行为，可以保证在一定范围内的绝对正确。基于形式化方法的研究在一些安全攸关的领域，如雷达、核电、航空、区块链等已经逐步得到应用，并且取得了非常好的效果。

常见雷达软件编程语言如C 语言可以编写可执行程序，具有图灵完备属性，实现较为复杂的功能，但是其安全性较差，容易产生漏洞，如整数溢出、数组越界、函数重入等等，从而给软件安全带来潜在的威胁，造成不可预料的损失。一阶逻辑是具有明确语法和语义的形式语言，且具有丰富的表达能力，可用于规约、定理证明和模型检测。

本文提出从C 程序到基于一阶逻辑的形式模型的转换方法，首先定义了C 语言的核心子集，通过定义辅助运算子，给出了保持语义一致的映射关系，从而使用基于一阶逻辑的形式模型来规约C 程序语言，包括赋值语句、条件语句、循环语句以及函数的规约，指导生成的形式模型可以自动地被验证工具执行并验证程序的正确性，有效提高了C 程序的安全性，以及程序验证的效率。

1 总体转换方法

我们提出基于形式模型的C 程序建模与验证方法，如图1所示，一个C 程序主要包括赋值语句、条件语句、循环语句以及函数结构，我们为每一个元素建立了与其语义保持一致的形式模型。其中，我们考虑C 语言子集包括：

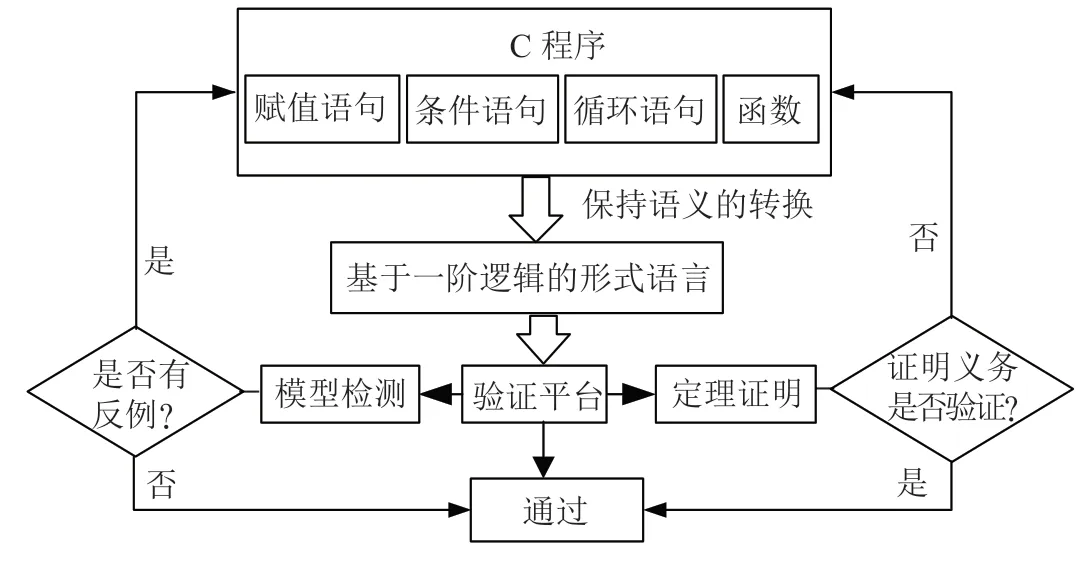
图1 C 程序建模与验证方法

（1）赋值语句：{p1, v=e, p2},其中p1,p2 表示赋值语句执行前后的程序，v 表示程序变量，e 为表达式；

（2）条件语句if: {p1,if (Cond(v)) e1 else e2,p2},其中Cond(v),表示从包含变量集合v 的布尔表达式到true 或者false 布尔值的映射，e1,e2 为语句集合；

（3）循环语句while：{p1, while(Cond(v)){e},p2}，其中e 为循环体内部语句集合；

（4）函数定义{p1,return_t func_name(para_list){e},p2},其中return_t 为函数返回值类型，func_name 为函数名，para_list 为包含参数类型和参数名的列表，e 表示函数体的语句集合。

目标形式模型基于一阶逻辑，其语法包括：

（1）量化符号∀和∃；

（2）逻辑连接词蕴含→、否定¬、双条件↔、且∧以及或∨；

（3）括号、方括号以及其他自定义标点符号；

（4）集合的变量，通常标记为英文字母的小写形式如，，等；

（5）等式符号=。

对于程序而言，用户最关心的是程序的安全属性是否得到满足，如类型检查、可达性、死锁、无状态二义性等。通过转换规则，可以使用基于一阶逻辑的形式语言对程序建模以及对期望属性规约。当得到形式模型后，可以进行模型转换，转换为更加复杂的形式模型。同时，借助验证平台，如Rodin，Isabelle，SPIN 等证明工具对模型进行验证与仿真。通过工具提供的交互式定理证明助手，自动验证生成的证明义务，从而验证模型是否满足给定的属性。对于一些状态比较简单的模型，可以通过模型检测工具，对状态空间进行搜索穷举，如果找到反例，则需要修改C 程序，反之，则通过验证。

2 转换规则

2.1 辅助运算子

我们首先定义ξ 操作符表示公式具有良好的条件。比如ξ（÷）：≠0，定义：

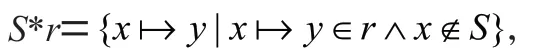
因此，可以定义＜+=∪（dom（）*），表示使用映射关系集合来更新集合中映射关系。更新表示如果有相同变量，则用中该变量的值来替代，如果中有新的变量，则引入该变量到该值的映射关系。

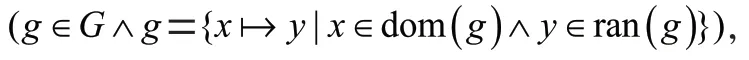
2.2 形式化规约

下面分别给出赋值语句、条件语句、循环语句以及函数的转换规则。

规定赋值语句的转化规则如下：

即，C 语言的赋值语句转换为一阶逻辑中对全局变量映射关系集合中变量的更新。

规定条件语句的转换规则如下：

即，首先将C 的条件语句转为0（false）和非0（true），然后基于一阶逻辑进行析取操作，当循环条件不满足时候，规定蕴含true，表示跳出循环

规定循环语句的转换规则如下，其中表示的后继。

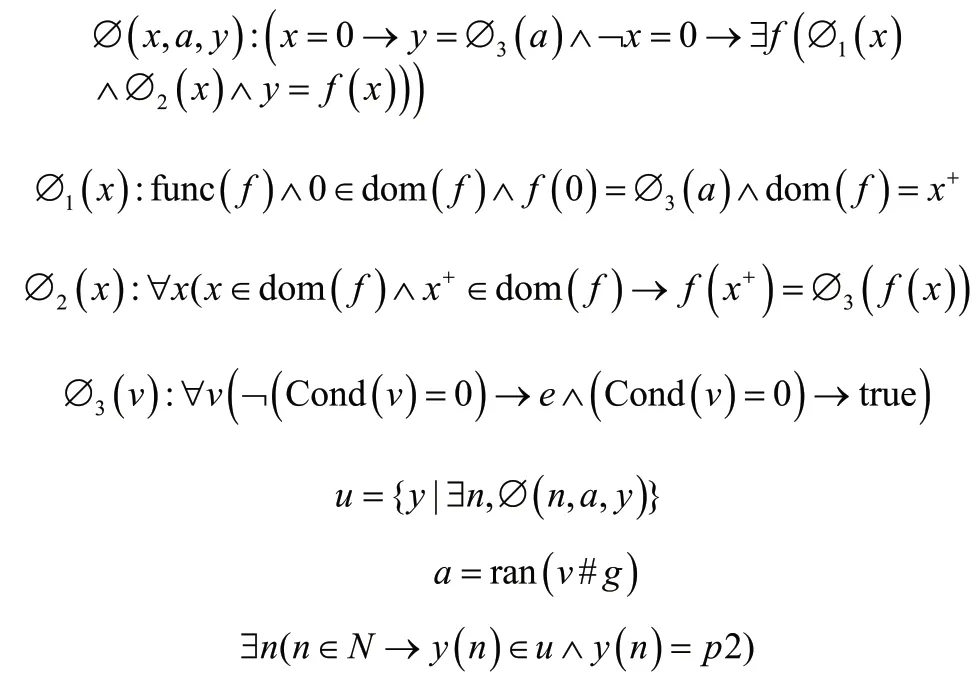
即，构造一个自然数到集合{∅（），∅（∅（）），…}的映射，每个∅（）函数对Cond（）进行判断并析取操作。存在某个自然数使得其对应的{∅（），∅（∅（）），…}的某个值为p2 语句的执行，跳出循环。

下面考虑函数定义的转换规则：

（1）函数自身没有调用其他函数（包括自己），形如：{p1, return_tfunc_name(para_list){body; return e},p2}，这里给出两种形式的转换规则。

第一种：

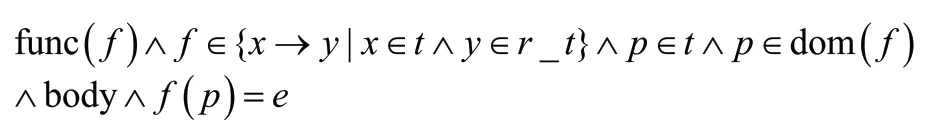
其中，_为返回值的类型，为参数类型，默认无参数为true，body 为函数体，为函数返回值。

第二种：

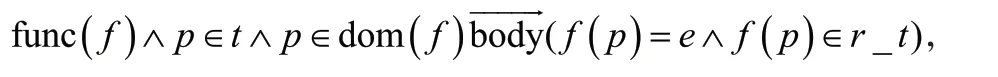
使用蕴含的形式，类似霍尔逻辑，表示经过函数体的执行后可以蕴含函数值的类型

（2）函数调用其他函数，形如：{p1,return_t func_name(para_list){func1(para) ;body},p2}

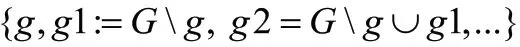
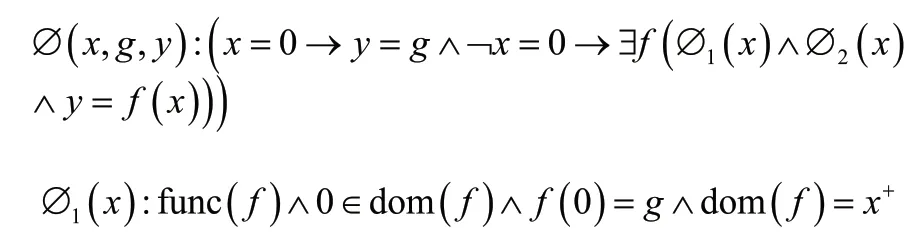
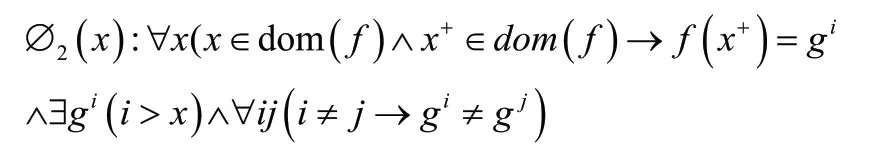
函数体内每调用一次其他函数，则触发该映射，生成新的全局变量映射g，和当前自然数x 一一对应，当＞，保证了g和之前的所有g（≤）不一样，用于保存调用函数的局部变量。如果是对全局变量更新，则对进行更新。

（3）函数递归调用自身，形如：{p1,return_t func_name(para_list){func_name(para_list) ;body},p2}

首先用一阶逻辑描述递归不动点定理，首先定义连续函数的集合：

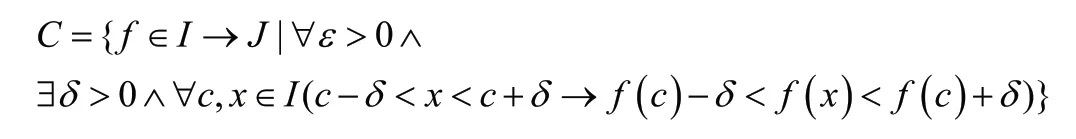
然后描述不动点定理：

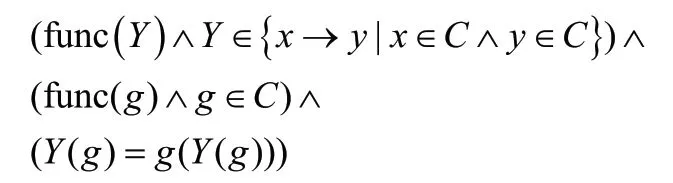
即任何连续函数都存在不动点。使用lambda 演算来表示上述形式函数，则，取参数，后的演算结果为

所以定义自然数集合到集合{（），（（）），…}的映射，表示递归的次数不断增加。

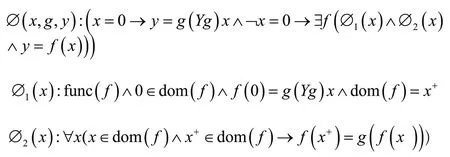
3 实例演示

以一个简单的C 程序为例，如表1所示，该程序包含赋值语句、条件语句、循环语句以及两个函数，其中一个函数是inf_1，递归调用自身，另外一个是main 函数，作为C程序的启动入口，其中调用inf_1 函数。C 程序案例：

根据上节给出的转换规则，可以得到基于一阶逻辑的形式模型：

该模型是基于一阶逻辑，与同样基于集合论的Event-B模型具有等价的语义，但是本文生成的形式模型比Event-B 模型的语法更加简单。因此，可以考虑将形式模型转换到Event-B 模型，借助Rodin 平台对Event-B 模型进行定理证明和模型检测。同样，有限状态机模型也是基于一阶逻辑，因此可以考虑将本文的形式模型转换到有限状态机模型，从而借助状态机可视化模型中状态的迁移过程。

4 结 论

本文以雷达软件安全为背景，研究了从C 程序到基于一阶逻辑的形式模型的转换方法，选取C 程序核心语法子集为对象，通过定义辅助运算子，建立了保持语义一致的映射关系，生成C 程序对应的形式模型，该模型是基于一阶逻辑语法的可执行模型，从而借助验证平台自动地进行定理证明和进行模型检测，验证了C 程序的属性，提高了程序的安全性。未来将进一步提高转换的自动化程度，实现自动转换的工具，并扩大C 程序的子集范围，该方法已经针对运用C程序语言的雷达系统进行了检验，对软件的测试更加充分，减少漏洞风险，具有重要的应用价值。