基于优选特征子集的厚板板形质量预测分析

邢玉鹏,张同康,陆 军,丁进良

(东北大学 流程工业综合自动化国家重点实验室，辽宁 沈阳 110819)

0 引言

钢铁工业是国家非常重要的基础工业之一，是国家经济的命脉[1]。厚板作为钢铁工业中重要的产品，广泛应用于基础设施、桥梁建造、船舶汽车、容器制造等行业。厚板加工过程中，许多过程变量(如加热炉炉温、轧制力、冷却水流量等)都会影响厚板板形质量，且厚板板形作为评价厚板产品的关键指标之一，会直接影响厚板产品的成材率，从而给企业带来经济损失、材料浪费、能源损耗、环境污染等问题。从过程变量中建立准确的厚板板形质量预测模型，寻找影响厚板板形质量的变量及权重，从而对厚板板形质量进行根因分析，是目前亟待解决的一个重要问题。

厚板生产过程是一个复杂的物理加工和化学反应过程，其生产过程主要包括加热阶段、轧制阶段、冷却阶段、热矫直阶段、板形质量检测阶段[2]。生产过程中包含的工序及变量众多。当某一个变量出现问题时，不可避免会影响其他变量，从而导致厚板板形出现问题。由于厚板生产是小批量、多阶段过程，难以明确影响厚板板形的生产过程变量，导致对厚板板形预测时，难以选取过程变量，以实现对厚板板形的准确预测，更无法进一步分析影响厚板板形的工序和变量重要性。

目前，针对厚板板形质量预测的研究主要是采用机理分析的方法，该类方法主要利用专家经验对厚板生产工序及变量进行机理分析，并结合实际生产过程分析影响板形的原因。如刘夏等[3]利用有限元方法和辊系的变形数据对板形进行分析，并提出简化的有限元分析方法，计算出板形、轧制力等信息。黎慧开等[4]从机理角度深入分析与厚板板形有关的变量，深入研究厚板板形的控制理论，选取与厚板板形控制相关的变量，建立了板形计算模型；张祖江等[5]针对板形中存在凸度大、楔形大、边浪严重等问题，通过理论分析以及对现场数据的跟踪查看，对影响厚板板形凸度和边浪严重的原因进行了研究，得出影响厚板板形凸度和边浪严重的原因是轧制过程中厚板宽度方向上的压下量两边大中间小，影响厚板板形楔形的原因是轧机传动侧和操作侧刚度不一致这两个结论。上述基于机理分析的模型对厚板板形质量分析主要考虑某一个工序的影响，未考虑使用厚板生产全流程数据对厚板板形进行质量预测。然而，厚板的全流程生产各工序之间影响密切，单独考虑某一工序会忽略各个工序之间的相关性，进而影响模型精度，以至无法从整体上分析影响厚板板形的工序及变量。此外，因为厚板板形生产全流程过程复杂，难以建立精确的机理模型，所以建模误差不可避免。

随着传感器技术的发展，工厂收集了大量的工业数据[6]，基于数据的厚板板形质量预测与分析方法受到了广泛关注，越来越多的研究倾向于利用生产过程数据预测板形质量。如HU等[7]采用基于互信息的深度置信网络对厚板板形质量进行建模，该方法首先利用互信息选择所需输入变量，然后采用深度置信网络建立板形平整度预测模型。曹建国等[8]利用厚板生产过程中轧制过程的历史数据建立随机森林预测模型，并利用关联规则挖掘算法寻找影响厚板质量的关键变量。以上方法旨在建立厚板板形质量预测模型，未考虑使用厚板生产全流程数据进行分析，也未考虑寻找引起厚板板形质量异常的变量及重要性。

厚板板形质量问题严重影响企业的生产效率和经济效益，因此亟需对其异常进行根因分析。针对该问题，何飞等[9]使用基于格兰杰因果关系的方法对厚板头部形状拉窄现象进行根因分析，该方法首先利用核熵成分分析判断带钢宽度是否存在故障，然后利用对比格兰杰因果关系对轧制工序中的变量进行分析，但该方法只对厚板板形轧制过程带钢头部拉窄现象进行了根因分析。BAHRAMI等[10]利用光学和电子显微镜对板形表面的裂纹进行了根因分析研究，从厚板的微观层面分析裂纹产生的原因，该方法只是对厚板热轧后表面开裂进行微观层面分析，未对厚板生产中的全流程数据进行根因分析。

目前针对厚板板形质量根因分析的研究较少，根因分析主要分为领域专家知识的根因分析和数据驱动的根因分析。基于领域专家知识的根因分析[12]需要将历史过程中出现问题的故障记录到系统中，当出现新的板形质量问题时，根据系统数据，由专家定位到该故障的原因。基于数据的根因分析又分为有监督学习的根因分析[12]和无监督学习的根因分析，其中有监督学习的根因分析如决策树[13]，该方法需要已知故障真实的原因标签，但实际厚板生产过程难以获得故障原因标签，因此无法采用该方法对其进行根因分析。基于无监督学习的根因分析，如关联规则算法[14](Apriori)，需要进行频繁项集的挖掘和关联规则的推断，且Apriori适用的场合局限性较大，该方法难以应用到实际的工业场景中，如厚板板形质量根因分析。综上所述，现有方法主要从单一工序分析影响板形的情况，没有利用生产全流程数据进行研究，这会忽略各工序之间的相关性，导致板形预测精度低，根因分析困难。鉴于厚板生产过程各工序间关系密切，有必要利用厚板生产经过的加热、轧制、冷却、矫直全流程数据对厚板板形进行质量预测与根因分析。

针对上述问题，本文提出一种具有根因分析能力的厚板板形质量预测模型(KPLS-MIGA)，从工业大数据中分析、挖掘各工序变量与板形质量隐含的关系。首先，考虑到厚板小批量生产、生产过程变量非线性强的特点，本文采用基于核偏最小二乘(Kernal Partial Least Squares, KPLS)方法建立厚板板形质量预测模型，对厚板板形质量进行准确预测。其次，为了对厚板板形质量进行根因分析，本文通过混合整数遗传算法(Mixed Integer Genetic Algorithm, MIGA)寻找影响厚板板形质量的最优参数，将MIGA集成到KPLS中，进行参数寻优，在训练过程中找寻最优参数，用于厚板板形质量预测和根因分析。最后，将本文所提算法应用到实际的厚板生产过程中，利用生产工艺和实际现场数据证明了所提方法的有效性与优越性。

1 厚板板形质量问题描述

厚板生产过程十分复杂，具有多工序、小批量、非线性强等特点，是典型的流程工业过程[15]。厚板生产的目标是获得性能好、质量合格、板形达标的产品，为了实现这一目标，应对厚板生产过程进行实时监测和有效控制。

在厚板生产过程中，厚板板形质量难以通过人眼检测，且现有的厚板板形检测工序需要等到厚板生产完成一段时间后，才能进行板形质量分析。若厚板板形故障未被及时检测出来，则很可能导致后续生产的厚板都出现类似的问题，这样会在很大程度上增加企业产品的不合格率，大幅提高企业的生产成本，因此需要利用生产过程变量对厚板板形质量进行准确预测和根因分析。

在厚板生产过程中，板坯依次经过加热、轧制、冷却(Accelerated Cooling, ACC)、矫直等工序，加工成合格的钢板[16]。厚板生产工序流程图如图1所示。厚板的原材料板坯依次经过测重、测长、测温后，进入加热过程进行加热，板坯在加热炉内通过步进梁的上升、前进运动，依次经过加热炉中的预热段、多个加热段、均热段，最终温度达到轧制所需温度[17]。

厚板加热过程会改变厚板内部金属的结晶组织，若内外温度不均匀会影响厚板板形质量，因此待板坯升温到所需温度后，才能进入轧制过程，依次进行除磷、粗轧和精轧3个环节。由于厚板在加热时表面会生成一次氧化铁皮，在轧制之前需要经过除磷操作，利用高压水的强烈冲击，去除厚板表面的氧化铁皮，从而避免因磷过多使得厚板的冷脆性增加，导致后续轧制过程板形出现问题。除磷后厚板依次进行粗轧和精轧过程，粗轧阶段在粗轧机中完成，主要将板坯或扁锭展宽到所需要的宽度，并进行大压缩延伸，同时尽量保证厚板的四周为平整的直线。精轧阶段主要在精轧机中完成，主要控制钢板厚度、板形质量、表面质量和性能，保证厚板板形平整，厚度符合最终指标要求。厚板在经过轧制阶段后，需要进行加速冷却，冷却会直接影响厚板的温度场分布，若冷却不均匀，会导致板形出现问题，因此需均匀冷却整个厚板，使厚板的温度快速下降，达到冷却标准，从而提高厚板的强度和焊接性。

厚板在上述工序中不可避免会出现一些缺陷，如瓢曲或波浪问题，需要经过热矫直工序对之前的厚板板形缺陷进行矫直，使板形质量尽可能合格[18]，但即使经过这些过程，仍有较大比例的厚板板形会出现问题，这会严重影响企业的生产效率。

在上述生产过程中，影响板形质量的主要是板坯在生产过程受到的温度及轧制力。如加热阶段中加热炉的炉温、出炉平均温度、加热段时间、板坯表面温度；轧制阶段的轧制力、弯辊力、压下率；冷却阶段的冷却水流量、终冷温度标准差、冷却率等，这些都有可能会对板形的应力产生影响，从而导致板形质量缺陷。在实际工业过程中，现有的专家经验并不能定位出哪些变量导致厚板板形质量异常，因此需要对厚板板形进行预测并进行根因分析，寻找影响厚板板形质量的工序及变量重要性。

2 厚板板形质量预测与变量根因分析

2.1 基本方法介绍

2.1.1 核偏最小二乘

作为数据驱动多变量质量预测的主流技术,偏最小二乘(PLS)[19]是一种流行的多变量统计方法，旨在寻找特定的自变量(如厚板生产过程变量)与待预测变量(如厚板板形质量评价指标)之间的关联关系。PLS的主要优点是建立厚板生产过程变量与板形之间的关系模型，能够有效解决多变量之间的耦合性、数据样本少的问题。实际厚板工艺存在明显的非线性特点，常规PLS作为线性降维投影方法,很难捕捉生产过程的非线性结构。基于核函数的PLS又称为核函数潜投影结构,与其他非线性PLS方法相比，KPLS的优点在于可以非线性抽取输入特征的正交分量，因而成为主流的非线性过程质量预测方法。基于核函数的偏最小二乘方法是通过结合核函数与传统的PLS方法对数据中的非线性关系进行建模。设非线性系统的输入变量为X=[x1,x2,…,xn]T∈Rn×p，待预测变量Y=[y1,y2,…,yn]T∈Rn×q。其中：n为样本数量，p为输入变量维数，q为待预测变量维数。定义映射矩阵Φ=[φ(x1),φ(x2),…,φ(xn)]T∈Rn×f，其中φ为非线性函数，通过核函数计算K=ΦΦT，KPLS质量预测步骤[20]如下所示：

(1)令i=1，K1=K,Y1=Y；

(2)设ui等于Yi的任何一列；

(3)ti=Kiui,ti←ti/‖ti‖；

(5)ui=Yiqi,ui←ui/‖ui‖；

(6)若ti收敛，转步骤(7),否则，转步骤(3)；

(8)令i=i+1，若i>p，则终止循环，否则，转步骤(2)。

2.1.2 混合整数遗传算法(MIGA)

为了寻找影响厚板板形质量的生产过程变量，需要优化过程变量的选择及其对板形的重要性，找寻最优的参数，用于厚板板形质量的根因分析，其中过程变量是否选择参与建模是一个整数型优化问题，遗传算法(GA)[21]作为一种典型的进化计算算法，更加适合在离散问题上寻找最优参数。该算法通过模拟生物界自然选择和自然遗传机制实现最优解的搜索，能够有效解决复杂的非线性优化问题，目前已被广泛应用于建模预测等领域。GA首先通过选择输入变量编码成的染色体，产生初始种群；之后通过选择、交叉和变异操作产生新一代种群，根据适应度函数值选择最优个体，直到达到优化停止条件；最后将适应度值最高的个体解码，从而获取模型的最佳参数。由于过程变量是否选择参与建模是整数型优化问题，过程变量重要性是实数型优化问题，本文使用混合整数遗传算法[22]，一方面优化输入变量的选择，另一方面赋予不同的输入变量对输出的重要性程度，能够辅助显示变量的重要性，从而寻找到影响厚板板形的过程变量及其重要性。

2.2 基于KPLS-MIGA厚板板形质量预测和根因分析

世界各国将厚板的质量作为衡量一个国家钢铁工业综合水平的重要指标，当前主要从板形、尺寸、性能、表面、内质5个方面对厚板质量进行评价，其中由于厚板板形异常导致厚板产品不合格所占比重最高，且厚板板形质量控制复杂。因此，亟需对厚板板形进行建模预测，并寻找影响厚板板形质量的关键工序和变量。由上述厚板生产过程的描述可知，生产过程中存在许多变量，如加热阶段的温度、轧制阶段的轧制力、冷却阶段的冷却率等，都会影响厚板板形质量，本文利用以上过程变量对厚板板形质量进行预测和根因分析。

实际厚板生产过程中，由于全流程的不同工序的变量间存在非线性关系，当厚板产品质量出现问题时，难以定位影响厚板板形质量的关键工序和变量。本文采用MIGA方法，从全流程的数据中选择影响厚板生产过程的工序和变量重要性，然后通过KPLS建立厚板质量预测模型，将厚板生产过程变量映射到高维特征空间，用于厚板板形质量非线性建模分析。通过不断迭代参数，输出最优的预测结果，得出影响厚板的过程工序及变量重要性。

2.2.1 KPLS-MIGA建模

KPLS通过使用核函数替代内积，隐式将非线性的训练数据映射到高维空间，可以选用不同的核函数处理不同的非线性关系，常用的核函数包括线性核函数、径向基核函数、Sigmoid核函数、多项式核函数。本文选取径向基核函数将自变量映射到高维空间得到核矩阵。训练样本集为X=[x1,x2,…,xn]T∈Rn×p，其中：n为训练样本数量，p个过程变量维数。待预测变量Y=[y1,y2,…,yn]T∈Rn×1，1个待预测变量(厚板板形质量指标),通过径向基核函数得到核矩阵K:

(1)

之后建立KPLS回归预测模型

Yc=KB,

B=U(TTKU)-1TTY。

(2)

其中:B为KPLS的系数矩阵；T、U分别为KPLS从Φ和Y中提取的主成分矩阵；Y为训练集中因变量矩阵，Yc为训练集中的因变量预测矩阵。

为验证本文所提算法的有效性，对测试样本Xt=[x1,x2,…,xn1]T∈Rn1×p和Yt=[y1,y2,…,yn1]T∈Rn1×1进行预测，其中n1为测试样本数量。首先计算测试样本Xt与训练样本X之间的核矩阵Kt=[k(x(i),k(j))]n1×n，之后利用训练数据的核矩阵K对测试集数据的核矩阵Kt中心化，最终进行厚板板形质量预测。

Yt=KtB，

B=U(TTKtU)-1TTY。

(3)

2.2.2 KPLS-MIGA参数优化与根因分析

由于在建模过程中难以得知生产过程变量与厚板板形之间的影响关系，本文采用MIGA对输入变量进行选择，输入变量“1”代表选择该变量参与建模，“0”代表未选择该变量参与建模。假设S={s1,s2,…,sN}表示厚板生产过程变量是否选择编码成的染色体，Eval(S)表示S的验证集误差，H表示选择用于建模的生产过程变量重要性，种群经过不断迭代优化，寻找到最优的染色体，解码获得最优的厚板生产过程变量。

由于需要同时优化变量选择和变量权重，从而对厚板板形进行质量预测，本文采用MIGA优化生产过程变量及其重要性，目标是选择最佳个体用于KPLS厚板板形质量建模，最小化适应度函数。数据集分为训练集、验证集和测试集，其中训练集用于训练模型，验证集用来寻找最佳参数，测试集用于模型预测。基于KPLS-MIGA方法在验证集的预测误差为：

(4)

f(S,H)=1/f(S,H)。

(5)

通过将适应度最小的个体解码，得到厚板板形质量预测模型的最优参数，该参数可以用于分析影响厚板板形质量的工序及变量重要性，然后通过MIGA优化选出过程变量及权重，建立KPLS-MIGA模型，同时对测试集的厚板板形进行预测。

2.2.3 KPLS-MIGA训练过程

在KPLS厚板板形预测模型训练的过程中，需要进行特征寻优，验证集作为待预测的样本，通过适应度函数，利用MIGA对输入过程工序和变量进行优化，首先对训练集建立预测模型，然后通过最小化验证集厚板板形预测精度，选择最佳的参数，使得验证集的厚板板形预测精度最高，最终将该参数用于测试集的厚板板形质量预测与根因分析。

KPLS-MIGA厚板板形预测建模主要步骤如下：

步骤1算法的初始化，根据优化的问题，确定种群规模、最大迭代次数、个体初始化。

步骤2根据已建立好的待优化问题的数学模型，对验证集建立KPLS模型得出适应度函数，计算每个个体的适应度值。

步骤3MIGA算法搜索阶段，优化选择输入工序及变量，依次经过选择、交叉、变异操作，直至达到停止条件，将适应度值最高的染色体解码，获得影响厚板板形质量的工序及变量。

步骤4建立KPLS-MIGA模型，对测试集的厚板板形进行预测。算法结构框图如图2所示。

3 实验研究

3.1 数据预处理

3.1.1 厚板生产过程变量预处理

本文利用中国某钢厂实际生产过程中采集的数据来验证所提方法的有效性和实用性，由于厚板产品是不同规格厚板批次生产，不同规格厚板加工过程存在差异，这对厚板板形质量预测与根因分析存在干扰。因此，本文首先从历史数据库中筛选出同种规格(相同型号、相同板坯厚度、相同目标厚度)的厚板用于后续分析，由于实际工业过程数据质量不高，还需要进一步进行数据清洗工作，如对筛选出来的厚板数据进行缺失值和明显异常值的清洗工作。

由于历史数据中根据规格筛选出的种类很多，本文使用某一规格钢板进行实验分析，经过数据清洗之后，最终选取1 368个样本进行后续研究。由于每个样本有上百个变量，本文根据专家知识和生产工艺，从变量中初步确定35个生产过程变量进行后续建模，即在实际的生产过程数据中选取1 368个样本、35个生产过程变量用于厚板板形质量预测与根因分析。

由于生产过程变量之间数据分布和范围存在较大差异，本文使用KPLS对厚板板形质量进行预测分析时，需要对厚板样本中的每个变量数据进行归一化，本文采用的归一化方法公式如下：

(6)

3.1.2 厚板板形指标预处理

厚板在经过所有工序加工之后，进行质量检测，对板形指标进行评估。在质量检测过程中，板形仪抽样均匀采集板形各个点的上表面距离辊道的距离，得到用于评价厚板板形指标的二维板形矩阵。该矩阵能够反映厚板板形在不同位置的厚度指标，能够表征板形的整体分布及变化。

本文通过将厚板二维分布矩阵进行处理从而得到每个厚板板形的质量评价指标。通过将超限点的数值进行绝对值的求和，用来表征每个厚板的板形变形程度，同时考虑到不同的厚板长度不一致，因此本文利用采样点绝对值之和占整体点的比例得出最终厚板板形的指标，即厚板板形质量得分。板形仪对某个厚板测量的点数据可视化后的热力图如图3所示，从图中可以看出厚板在不同位置的厚度分布，其中红色越深说明该厚板在该位置的板形质量越差。定义厚板板形质量评价指标

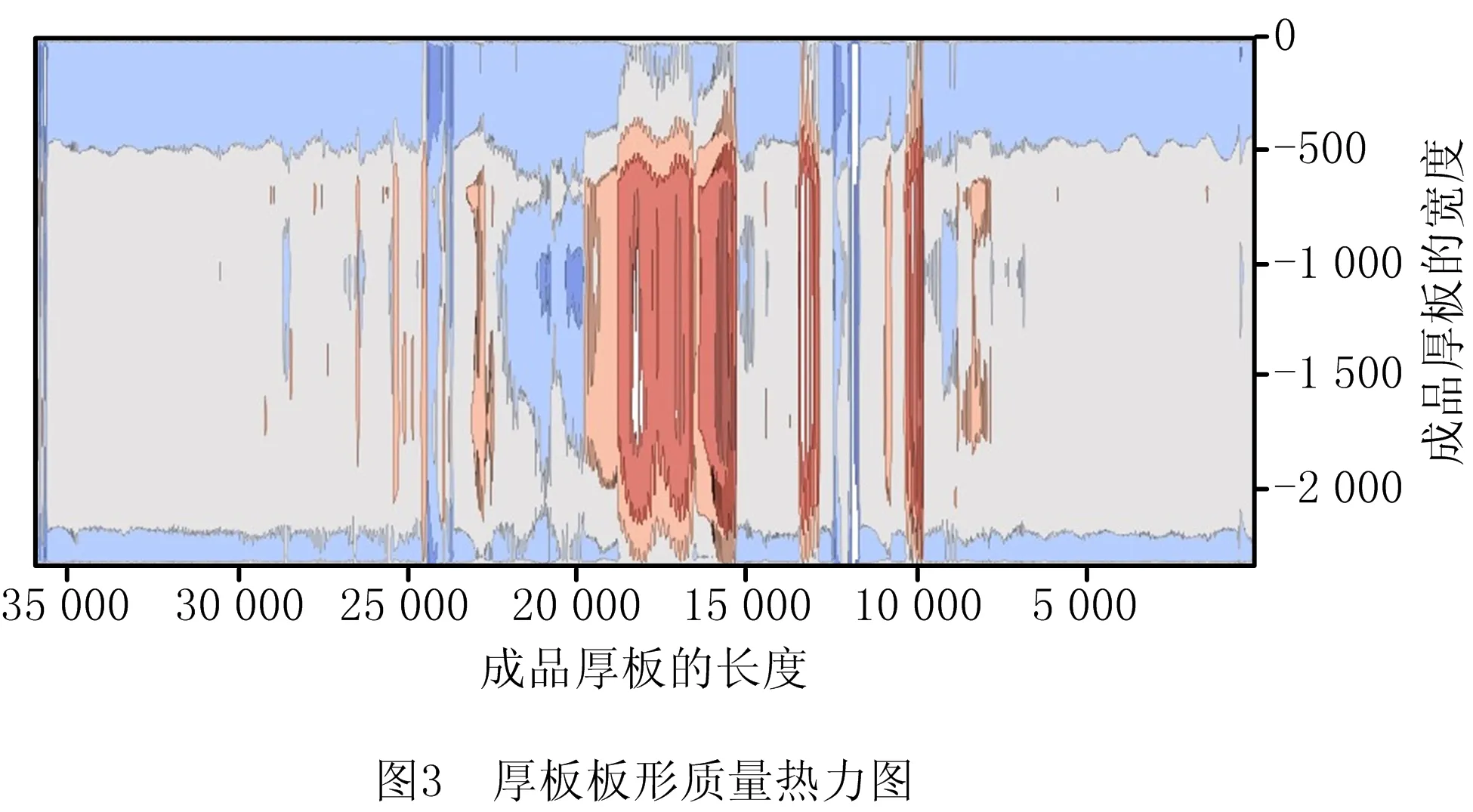
yshape=xss/xnum。

(7)

式中：yshape为定义的厚板板形质量指标，xss为采样点绝对值之和，xnum为采样点数量。

3.1.3 评价指标

本文采用预测值和真实值的均方根误差、平均绝对误差、决定性系数作为评估算法准确性的指标，其计算公式如下：

(1)均方根误差(RMSE)：

(8)

(2)平均绝对误差(MAE)：

(9)

(3)决定性系数R2：

(10)

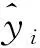
3.2 基于KPLS-MIGA厚板板形质量预测结果

通过在某钢铁生产车间选取同种规格的厚板、过程变量、厚板板形进行实验，利用实际采集的工业数据对厚板板形质量进行预测，厚板板形预测效果如图4所示，图中：蓝色为真实厚板板形质量指标，红色为本文所提算法厚板板形质量预测效果。可以看出，本文所提算法能够很好地对厚板板形质量进行预测。

为了进一步说明所提算法的有效性，将本文算法与其他算法进行比较。不同算法的厚板板形预测效果如图5所示。其中：图5a表示不同算法对厚板板形质量的预测曲线，图5b表示不同算法对厚板板形质量的预测偏差。从图中可以看出，所提算法能够更好地跟踪厚板板形的质量趋势，且最能逼近厚板板形质量。因此，本文所提算法对厚板板形质量预测偏差最小，效果最好。

不同算法评价指标如表1所示。从表中能够看出，本文所提基于KPLS-MIGA厚板板形质量预测方法在各项评价指标上都呈现出最好的结果，能够更好地拟合厚板板形质量变化，这是由于所提算法使用MIGA对变量及权重进行优化，选择重要的变量建立厚板板形质量预测模型，同时充分考虑了厚板生产过程中的小批量生产、变量非线性强等过程特性。由表1中的实验结果可以看出，基于KPLS-MIGA算法的RMSE和MAE最小，R2值最大，这表明所提方法预测更加准确，模型更加可靠。

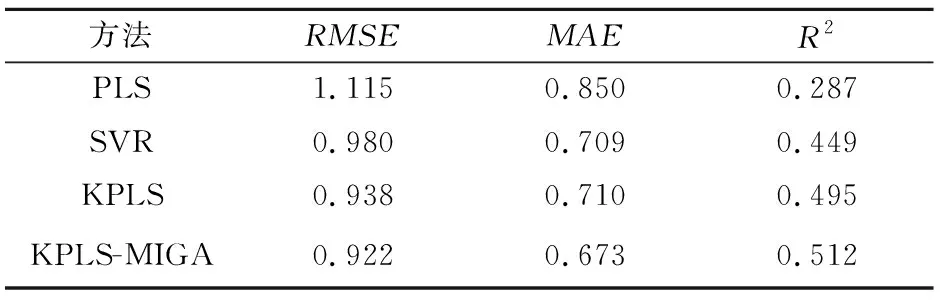
表1 厚板板形质量预测效果

3.3 基于KPLS-MIGA厚板板形质量根因分析

针对厚板板形质量根因分析问题，本文选取所提算法预测效果最好时对应的生产工序及变量，分别表示影响厚板质量的过程工序及变量，从而得出影响厚板板形质量的变量及其重要性。由于所提算法的预测效果能够很好地表征厚板板形质量，可说明本文算法选择的参数是准确可靠的。通过对MIGA最优参数解码得到生产过程工序及变量重要性如图6所示。若图中横坐标变量的值为0，代表该变量未参与模型的构建，因此忽略其对厚板板形质量的影响，只有当变量的值大于0时，此时变量才被选择放入KPLS-MIGA模型进行厚板板形质量预测和根因分析，变量不同的权重进一步说明参与建模的变量重要性的强弱。

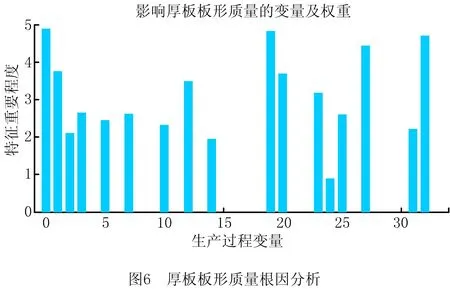
通过将实验分析出的工序及变量与真实的生产过程进行对比。能够得出影响厚板板形质量的主要是加热阶段中的预热段、加热段、均热段时间，加热段的入口平均温度；轧制阶段中的粗轧机道次、粗轧开轧温度、精轧机最后道次压下率、终轧温度偏差；冷却阶段中实际冷却率的变化、实际冷却率偏差。其中最重要的过程变量依次为预热段时间、精轧机最后道次压下率、冷却率偏差、冷却率平均值和加热I段温度。在实际厚板生产过程中，加热阶段作为厚板生产过程中第一个重要工序，为后续的轧制过程提供加热均匀的热钢坯，其中影响加热效果的重要变量有各加热阶段的时间，加热段的温度；轧制阶段作为厚板板形成形的关键阶段，影响轧制效果的主要是轧制点的温度和精轧机最后道次压下率，因而对板形有较大影响。冷却阶段是距离成品最近的工序，影响冷却效果的主要是厚板在长度、宽度、厚度方向上的不均匀冷却，由于冷却率是厚板温度随时间下降的速率，能够很好地表征冷却过程加工效果。本文所得实验结论与工艺知识一致，进一步说明了所提方法的有效性。

通过实验结果能够看出,KPLS-MIGA对厚板板形的预测误差最低，波动范围最小，模型可靠性更高。这是因为相较于其他方法，本文方法充分考虑了厚板实际生产过程特性(如小批量、非线性)。在建模过程中利用混合整数遗传算法筛选出最能表征板形质量的过程工序及变量重要性，然后利用KPLS对厚板板形质量非线性建模，使用训练好的KPLS-MIGA模型对测试集数据进行预测；最后解码MIGA参数，将算法寻找出的过程工序及变量重要性用于厚板板形质量根因分析。可以看出，本文所提KPLS-MIGA模型，不仅能够对厚板板形质量进行准确预测，还能够分析影响厚板板形质量的根本原因，具有很好的工业应用价值。

4 结束语

厚板板形质量稳定是提高企业综合经济效益的有效手段之一，考虑到实际厚板生产过程中存在小批量生产、强非线性等特点，本文提出一种基于KPLS-MIGA厚板板形质量预测和根因分析方法。针对厚板板形质量预测问题，本文采用KPLS提取变量间的非线性特征建立厚板板形质量预测模型，对厚板板形质量准确预测。针对影响厚板板形重要的工序和过程变量，通过将MIGA集成到KPLS建模中，在KPLS建模过程中优化变量选择以及变量权重，输出最优的参数用于分析影响厚板板形质量的过程变量。最后，利用某钢厂的真实数据，验证了本文所提算法的有效性和优越性。本文算法得出的结论与实际的工艺分析一致，因此该方法可以为现场工程师的决策提供参考。由于厚板板形全流程生产涉及多个工序，下一步将考虑对工序进行分层之后，再对厚板板形进行质量预测及根因分析。