江山虎山运动公园体育馆屋盖结构设计

邵兴宇，许敏，魏剑，刘柳，车力，周翔

（中南建筑设计院股份有限公司，武汉 430071）

1 工程概况

江山虎山运动公园体育馆建筑面积为1.99×104m2，总座席数为4 046 座，为可举办国际单项赛事的甲级体育建筑。体育馆建筑效果图如图1 所示，建筑平面为107.9 m×98.8 m 矩形平面，地上3 层框架-剪力墙结构，檐口高度23.25 m，屋面最高点25.50 m。屋盖采用张弦梁结构，最大跨度约66 m。体育馆典型剖面图如图2 所示。

图1 江山虎山运动公园体育馆效果图

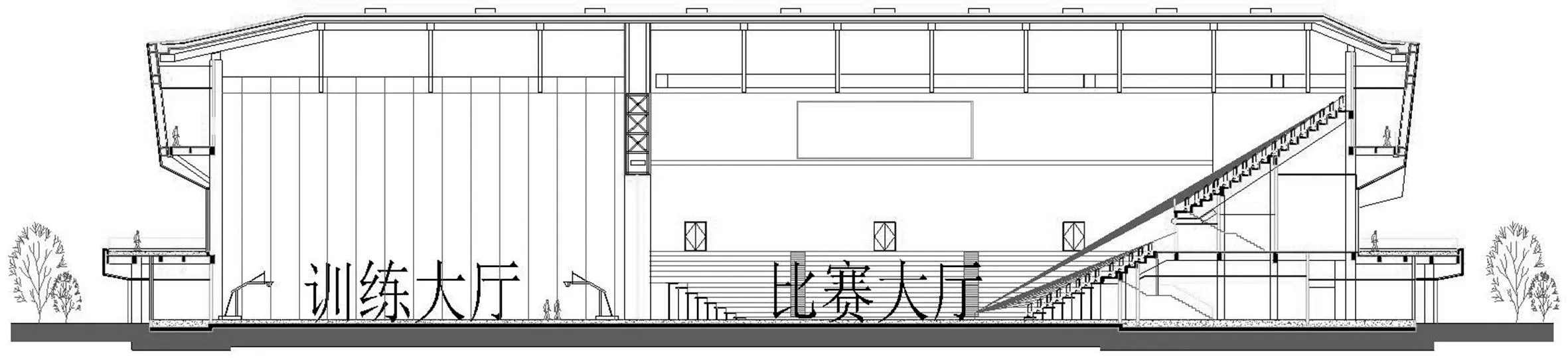
图2 体育馆典型截面剖面图

本工程项目设计使用年限为50 a，安全等级为二级[1]。根据GB 50223—2008《建筑工程抗震设防分类标准》[2]，本工程抗震设防烈度为6 度（0.05g），场地类别为Ⅱ类，抗震设防类别为标准设防类。框架抗震等级为四级，剪力墙抗震等级为三级，钢结构抗震等级为四级。

体育馆屋盖跨度大、重量轻，结构对风荷载和雪荷载敏感，采用重现期为100 a[3]的基本风压和雪压，基本风压取0.40 k N/m2，雪压取0.60 kN/m2。地面粗糙度为B 类。钢结构屋盖温度作用±35 ℃。

2 结构体系及布置

体育馆下部主体采用框架-剪力墙结构，柱、剪力墙以及梁板混凝土强度等级为C30，支撑屋盖框架柱截面为1 200 mm×1 200 mm。比赛大厅与训练厅上空区域尺寸为66 m×94.9 m，在垂直长边方向布置10 榀支撑与混凝土柱上的单向张弦梁，张弦梁主要间距为7.8 m，跨度66 m。单榀张弦梁上弦截面为600 mm×600 mm×20 mm×20 mm 的钢框梁，下弦拉索为直径90 mm 的高钒镀层索，最小破断荷载为6 899 k N，中间设置8根直径为299 mm 的支撑杆。两侧屋盖采用Y 形钢柱支撑，并用水平斜梁连接，Y 形柱提供较好的纵向抗侧刚度，水平斜梁提供较好的平面刚度。体育馆结构模型如图3 所示。江山虎山运动公园体育馆屋面钢结构平面布置图如图4 所示。

图3 体育馆结构模型

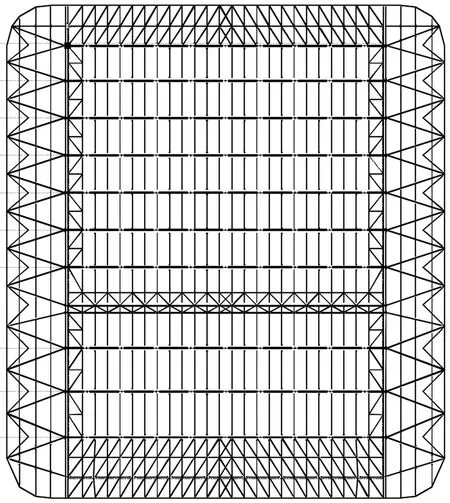
图4 屋面钢结构平面布置图

3 屋盖设计

张弦梁结构体系由上弦钢梁、竖向撑杆以及下弦拉索3部分构成。其中，梁为压弯构件、撑杆轴心受压、拉索承受拉力。由于张弦梁屋盖结构自重轻，结构可能在极端条件下以及荷载的不利布置时出现索退张的情况。设计中分析各种工况，确保拉索一直处于受拉状态。

张弦梁进行张拉时需要对拉力进行有效的控制，应不受两侧钢屋盖和下部混凝土结构的影响。本工程屋盖结构施工需要按如下顺序进行：

1）地面张弦梁拼装，同期两侧钢结构进行施工；

2）两榀张弦梁吊装并进行张拉（柱顶滑动），构件与两侧屋盖钢结构构件不连接；

3）屋面系统施工；

4）支座固定，与两侧屋盖钢梁连接。

在设计过程中，为准确计算屋盖的刚度，确保张弦梁结构的完成形状与建筑一致，采用SAP2000 进行了施工模拟，上弦、索以及竖向撑杆均采用梁单元进行模拟。将施工中张拉阶段实测数据与理论分析结果进行对比，部分结果见表1、表2。

表1 1-J、1-E 与1-D 轴变形

表2 1-J、1-E 与1-D 轴索拉力结果

由表1、表2 可以看出：在施工过程中，张弦梁实测拉力与挠度变形均与计算基本一致，且索力实测数据与理论数据误差控制在±6%以内，模拟施工结果与施工监测结果基本吻合。

4 断索分析

张弦梁结构通过给拉索施加预应力，可以形成屋盖的刚度，拉索承担较大拉力。若发生断索情况，可能给结构带来非常严重的影响。为了保证结构在断索后不至于倒塌，结构设计时假定索力最大的1-J 轴拉索在1.0 恒+1.0 活荷载作用下突然发生断裂，断索前后构件内力变化详见表3，体育馆竖向变形如图5 所示。

图5 1-J 轴拉索断索后体育馆竖向变形图（单位：mm）

表3 1-J 与1-H 轴断索前后构件内力变化结果

张弦梁拉索在发生断索后，张弦梁在荷载的作用下跨中最大竖向位移170 mm，为跨度的1/382，结构整体并没有发生较大的变形，断索的杆件及其相邻跨度构件荷载变化均在构件的承载能力范围内。即使张弦梁某根索发生突然断裂，屋盖结构整体也不会发生突然的坍塌。

5 稳定分析

张弦梁结构屋盖的稳定性可按考虑几何与材料非线性的有限元法进行计算。先进行线性屈曲分析，接续模拟施工后结构的整体刚度，在1.0 恒载+1.0 活载组合作用下，结构的第一阶模态为张弦梁的屈曲失稳如图6 所示，屈曲因子详见表4。

图6 第一阶屈曲模态

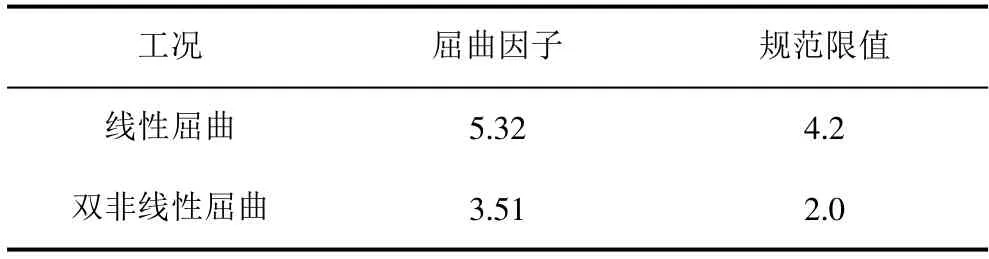
表4 屈曲因子

空间结构的整体稳定性能对初始缺陷非常敏感，存在初始缺陷的结构，其承载力会明显降低。结构整体稳定分析对初始缺陷的选取主要有两种分析方法：随机缺陷模态法和一致缺陷模态法。随机缺陷模态法虽然能够真实地反映实际结构，且所求得的临界荷载结果更能客观地反映所设计结构的情况，但由于需对不同缺陷分布进行多次非线性计算，更偏重于理论研究[4]。根据项目实际特点，本文采用一致缺陷模态法来设置模型的初始缺陷。

初始几何缺陷按最低阶屈曲模态分布时，求得的稳定性承载力是可能的最不利值。当缺陷大约达到跨度的1/300 时，其影响往往才充分展现。缺陷值为66.0（跨度）/300=0.22 m。在SAP 2000 中基于模态形状修改结构未变形的几何状态将第一阶屈曲模态的位移作为初始几何缺陷赋予结构。

材料非线性通过引入塑性铰来实现，塑性铰按照ASCE41-17—2017《既有建筑物的抗震评估与改造》中表9-7.1来定义。根据受力特点，张弦梁上弦采用P-M2-M3 铰，撑杆和索采用P 铰。

根据规范[5]第4.3 节内容，全过程分析的迭代方程如式（1）所示：

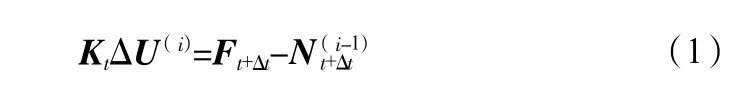
式中，Kt为t时刻结构的切线刚度矩阵；ΔU（i）为当前位移的迭代增量；Ft+Δt为t+Δt时刻外部所施加的节点荷载向量；为t+Δt时刻相应的杆件节点内力向量。

引入位移监测点，在1.0 恒载+1.0 活载组合作用下采用牛顿-拉夫森迭代法，得到荷载-位移曲线如图7 所示，屋盖结构达到极限承载历史的位移云图如图8 所示。塑性铰出现在上弦杆件上。

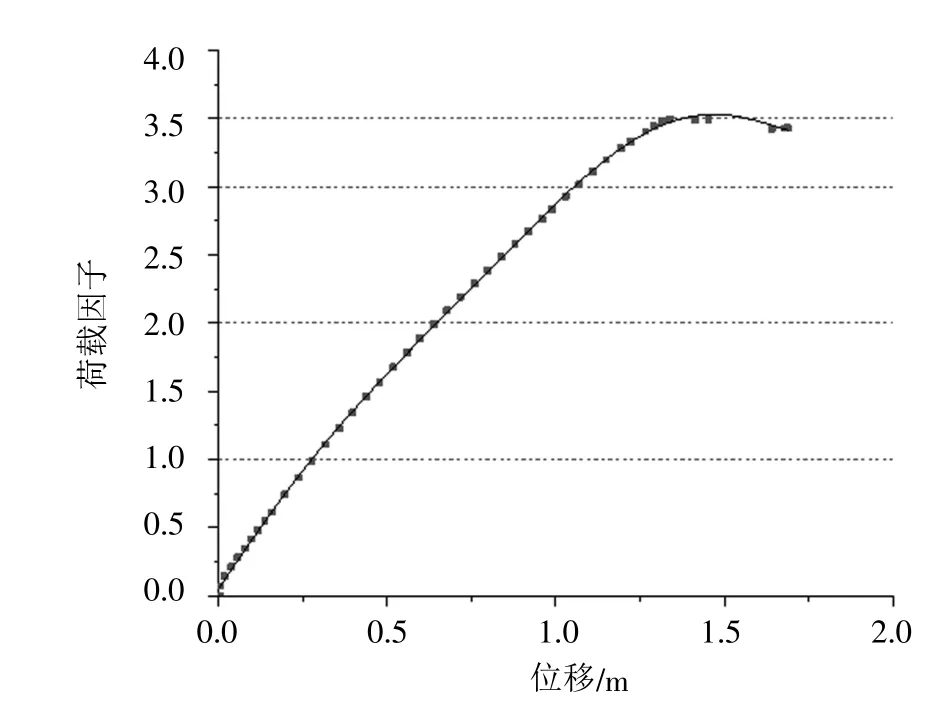
图7 双非线性荷载因子-位移曲线

图8 屋盖位移云图

结果表明：考虑初始缺陷的弹塑性全过程分析结构最大位移约为1.34 m，安全系数为3.51（见表4），结果均满足规范相关要求。

6 风洞试验

屋盖采用66 m 跨张弦梁结构，结构质量轻、刚度小，应当考虑风压脉动对结构产生风振的影响。屋盖结构的风振响应宜依据风洞试验结果按随机振动理论计算确定。

本工程风洞试验委托武汉大学结构风工程研究所完成，图9 为体育馆风洞试验模型。几何缩尺比为1∶100，试验风速为10 m/s，测点的采样频率为331 Hz，模型共布置了377 个测压点。同时，为了考虑邻近建筑物的影响，试验采用塑料泡沫及PVC 板复合制成模型对体育馆周围250 m 半径内的主要建筑物进行了模拟。

图9 体育馆风洞试验模型

试验通过旋转工作转盘，模拟0°～360°风向角的情况，其角度间隔为15°，测量24 个方向角下模型表面的风压力分布。通过对各测点脉动风压时程进行傅里叶变换，求得结构的风振响应和等效风荷载。

试验结果表明：

1）屋盖承受的风压主要以吸力（负压）为主，仅在局部位置有正压的情况出现。

2）100 a 重现期各风向作用下，极值风压最大值为1.31 kPa，极值风压最小值为-2.85 kPa，与选用规范方法计算结果基本一致。

3）体育馆顶部的等效静力风荷载较大，不仅由于强烈的流动分离引起较大的负压，亦因为较大的风振惯性力的组合作用使得局部节点产生较大的竖向等效静力风荷载。

7 结语

本文对江山虎山运动公园体育馆结构设计进行了介绍，阐述了项目的结构布置与结构体系，进行了屈曲分析、断索分析、稳定分析及风洞试验等。主要得出了以下结论：

1）将施工模拟数据与施工过程中的实测数据进行对比，模拟施工能够准确地反映结构在施工过程中的受力变化规律；

2）对体育馆结构进行断索分析表明，张弦梁下弦拉索发生突然断裂，屋盖结构整体也不会发生突然坍塌，结构设计较为合理；

3）根据空间网格结构技术规程，对屋盖进行了双非线性屈曲分析，能满足规范要求，结构具有较好的整体稳定性，承载能力较强；

4）本工程通过对体育馆模型进行风洞试验，得到了相应的风压数据，能够为相似的工程在进行结构设计时提供参考。