极端波浪条件下浅水系泊线张力陡增及应对方案
2022-08-11王德志王俊荣宮浩男朱魁星
王德志, 王俊荣,2*, 宮浩男, 朱魁星
(1. 中国海洋大学 工程学院, 山东 青岛 266100;2. 山东省海洋工程重点实验室, 山东 青岛 266100)
0 引 言
在海洋油气、海上风电等海上资源/能源开发中,浮式生产储卸装置(Floating Production Storage and Offloading,FPSO)、半潜式平台、Spar(单柱式平台)和张力腿平台(Tension Leg Platform,TLP)等浮式平台得到广泛的应用。系泊系统作为浮式平台常用的定位系统,关乎浮式结构系统的安全和相关作业的可靠性。系泊系统的设计需考虑系泊类型、锚泊半径、系泊线组成成分、安全准则等多方面因素。系泊方式有悬链线系泊和张紧式系泊:在水深小于1 000 m的情况下可采用悬链线系泊方式,特别在水深小于500 m的情况下,悬链线系泊方式成本更低;在水深大于1 000 m的情况下,张紧式系泊是更好的选择[1]。设计合理的系泊系统对浮式平台安全作业具有重要意义。
针对浮体系泊系统,国内外学者进行大量研究。ORMBERG等[2]提出浮体/系泊/立管系统的整体耦合动力分析方法,并指出非耦合分析可能会产生严重不准确的结果,特别是对于超深水。MA等[3]开发系泊浮体非线性耦合分析工具,研究Spar和TLP的运动响应。RAN[4]、GARRETT[5]、郑成荣[6]采用间接时域方法,应用细长杆理论对系泊浮体进行时域耦合动力分析。LOW等[7]提出一种频域/时域混合分析方法,其中,波频部分在频域中求解,低频部分在时域求解,与耦合时域分析方法相比,计算量低一个数量级,但是准确性相当。金瑞佳[8]、韩旭亮等[9]分别对系泊浮体进行全时域耦合分析,但是全时域方法仍在研究发展阶段。由上述文献不难发现,时域耦合动力分析已成为浮体系泊系统研究的主要分析方法,其中间接时域法在实际工程中得到广泛的应用。
目前,在浅水和中等水深海域一般使用悬链线系泊方式,但是在水深较浅的情况下,系泊线悬于水中的长度相对较短,较小的位移即引起系泊系统几何特性较大的变化,使系泊线容易进入张紧状态[10],由此容易出现张力陡增的现象。本文针对海洋平台在浅水恶劣海况下大幅运动时出现系泊线张力陡增的问题,以某半潜式平台为研究对象,采用数值分析方法建立平台湿表面模型,应用HydroD/Wadam软件,基于三维频域势流理论,得到平台频域水动力参数,通过DeepC/Simo/Riflex软件建立浮体-系泊系统模型,采用时域耦合动力分析方法得到浅水和中等水深情况下平台的运动响应和系泊线张力,研究系泊线张力陡增的成因,验证通过增加躺底段长度来优化系泊系统刚度,减小浅水系泊线张力陡增幅值的方法是有效可行的,并分析海床参数对系统响应特征的影响。
1 基本理论
1.1 系泊系统耦合分析方法
ORMBERG等[2]提出浮体/系泊/立管系统的整体耦合动力分析方法,空间离散系统的控制动态平衡方程可表示为
(1)
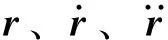
(2)
(3)
式中:M为系统的质量矩阵,包括结构质量、立管内部流体对整体质量的影响和水动力质量;C为系统的阻尼,包括结构内部阻尼、水动力阻尼和特定离散阻尼。内部相互作用力基于结构单元的瞬时应力状态得到,外力包括重力、浮力、平台运动产生的力、环境载荷和指定的节点集中力。
式(1)为非线性系统的微分方程,表示惯性力、阻尼力和外力矢量与结构位移、速度和加速度之间的关系,此外,内力与位移之间也存在着非线性关系。在计算求解时,浮体所受到的波浪激励力和势流阻尼由频域水动力分析得到的参数经过频转时的变换得到,细长构件所受的波浪载荷及其与浮体之间的相互作用则根据二者实时的位置状态进行计算,其耦合状态可采用Newmark-β方法和牛顿迭代法进行时域内的迭代求解。
1.2 系泊线刚度
系泊线刚度由几何刚度和弹性刚度组成。对于悬链线系泊,几何刚度由悬链线效应提供,弹性刚度由系泊线材料刚度EA和系泊线长度l决定,可表示为EA/l。系统刚度[1]可简单表示为
(4)
式中:kt为系泊线总刚度;ke为系泊线弹性刚度;kg为系泊线几何刚度。
1.3 系泊线与海床接触载荷
系泊线与海床的接触分为垂直于海床平面的接触和海床平面内的接触[11]。对于垂直于海床平面的接触,用弹簧刚度描述系泊线与海床的相互作用,该刚度给出系泊线每单位长度单位凹陷深度与海床的相互作用力。对于躺在海床上的系泊线单元,弹簧力与单元在水下的重量保持平衡,凹陷深度δ可表示为
(5)
式中:δ为凹陷深度;ws为系泊线单位长度的水下重量;kn为海床法向刚度参数。系泊线单元节点法向力可表示为
(6)
式中:Fn为节点法向力;Le为单元长度。
平行于海床平面的接触被建模为初始弹簧和滑动引起的摩擦力的组合。引入参考距离,表示节点沿系泊线轴向或横向的位移增量之和:当节点不发生滑动时,由参考距离和弹簧刚度参数计算相互作用力;当节点发生滑动时,由法向力和摩擦因数计算相互作用力。相互作用力可表示为
(7)
(8)
式中:Fa、Fl分别为节点受到的沿系泊线轴向和横向的作用力;ka、kl分别为海床平面内沿系泊线轴向和横向的刚度参数;δa、δl分别为沿系泊线轴向和横向的参考距离;μa、μl分别为沿系泊线轴向和横向的摩擦因数。
1.4 响应预报
时域耦合动力计算响应预报根据必维船级社(BV)规范[12]进行。计算时每个工况选取5个不同的随机种子,得到5个不同的时历结果,每个时历结果计算时长为3 h,时间步长取0.1 s。将各时历结果进行统计分析,得到该工况下的响应预报值,具体计算过程由以下公式给出:
SD=SM+aSS
(9)
(10)
(11)
式(9)~式(11)中:SD为响应预报值;SM为各随机种子下响应最值的平均;a为因数,当随机种子数n=5时,a取0.6;SS为各随机种子下响应最值的标准差;Sk为某随机种子下响应的最大值,k=1,2,…,n,此处取5。
2 数值模型
为研究浅水系泊系统在极端波浪作用下的张力陡增问题,采用间接时域法建立半潜式平台湿表面模型,对半潜式平台进行频域水动力分析,得到附加质量、辐射阻尼、一阶和二阶波浪激励力等水动力参数,由傅里叶变换将频域水动力参数转换为时域水动力载荷,建立平台/系泊系统时域耦合动力模型,模拟系泊系统力学响应行为。
2.1 平台主尺度
目标平台为双下浮体、四立柱的半潜式平台。平台生存工况吃水为16 m,排水量为48 083.1 t,其主尺度参数如表1所示。
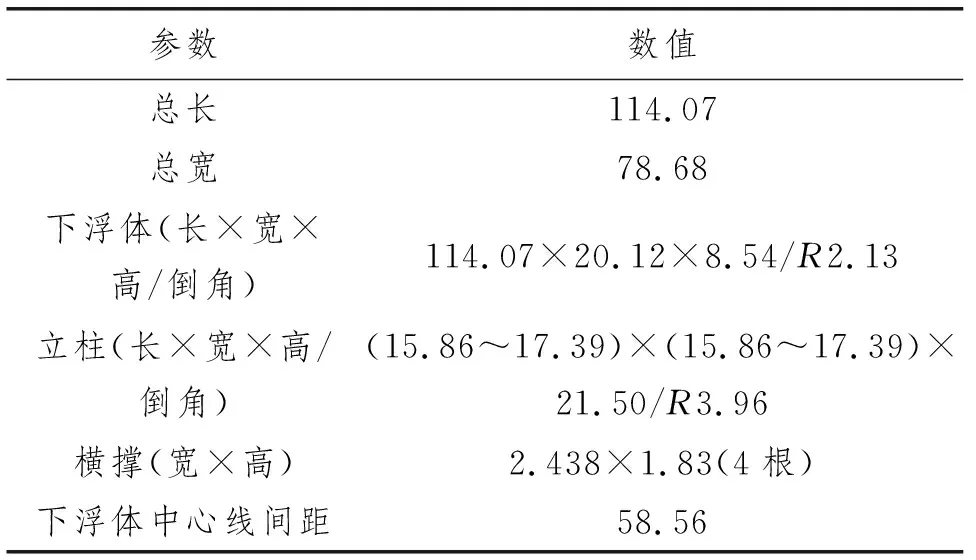
表1 半潜式平台主尺度 m
2.2 系泊系统参数
平台采用12点布锚悬链线系泊方式,系泊系统由4组成分相同的系泊线组成,每组包括3根系泊线,共12根,系泊线与xz平面的水平夹角为37°、40°、45°,导缆孔位于4根立柱的外侧,考虑平台作业水深为100 m和500 m两种情况。平台系泊系统布置如图1所示。
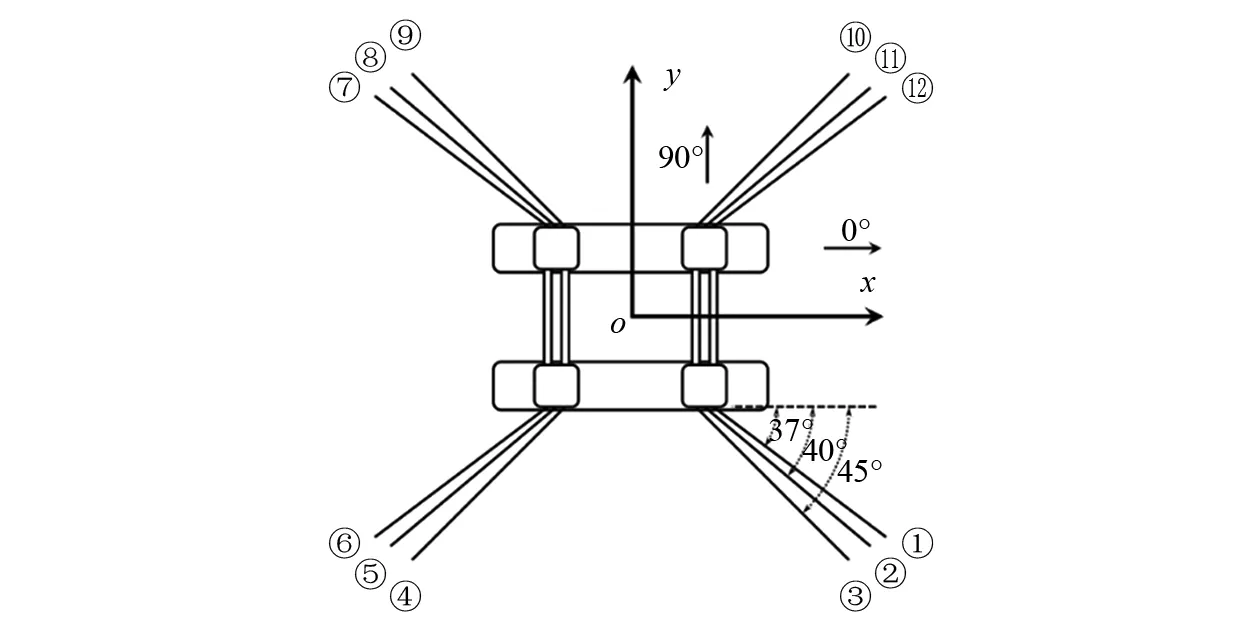
图1 系泊系统布置
通过DeepC软件建立数值模型,系泊线上部与平台导缆孔连接,下部与锚点连接,100 m水深系泊线采用全锚链形式,500 m水深采用锚链-钢缆-锚链的形式,系泊线基本参数如表2所示,DeepC数值模型如图2所示,静力状态下系泊线呈悬链线形状,构型如图3所示。

表2 系泊线参数
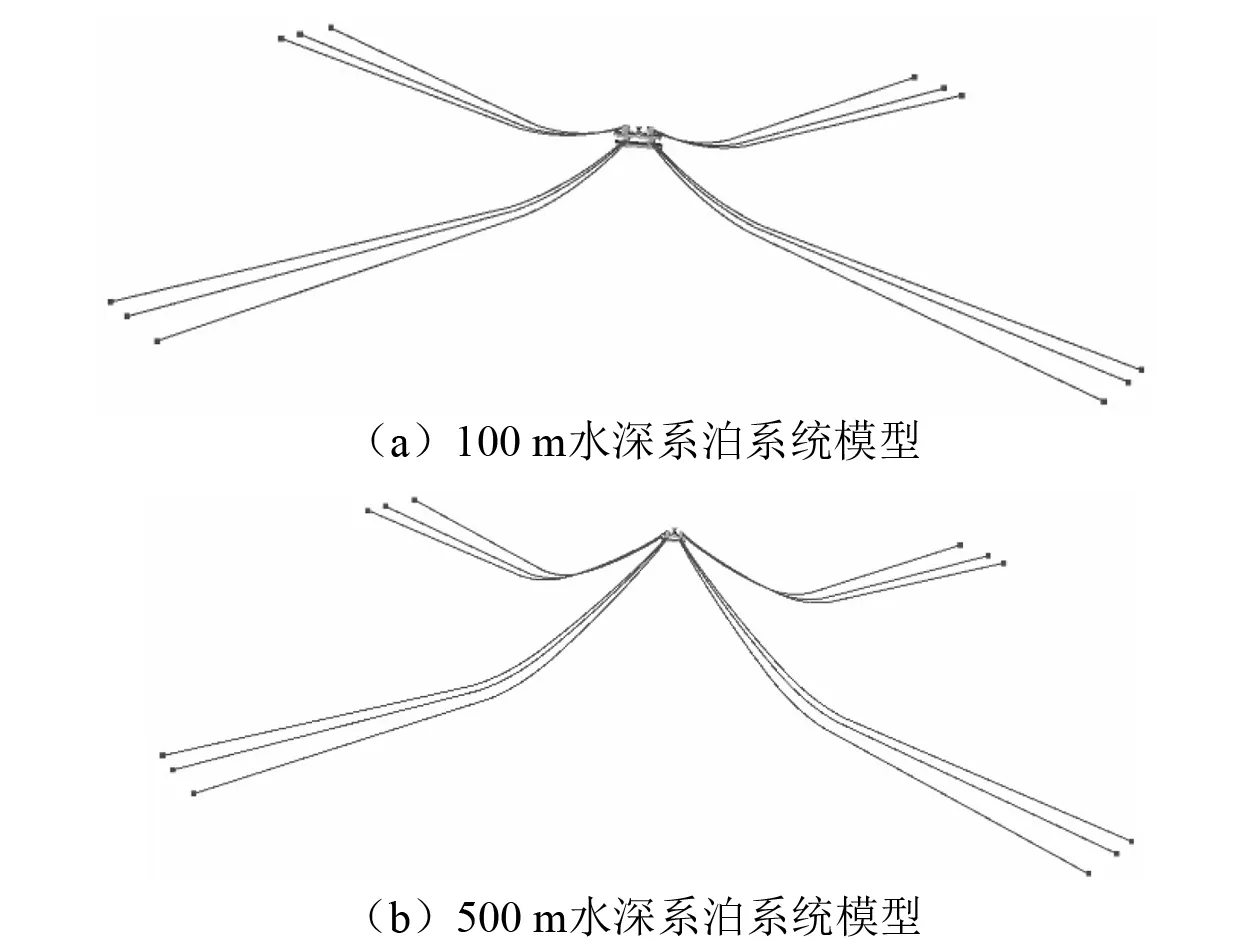
图2 DeepC系泊系统数值模型
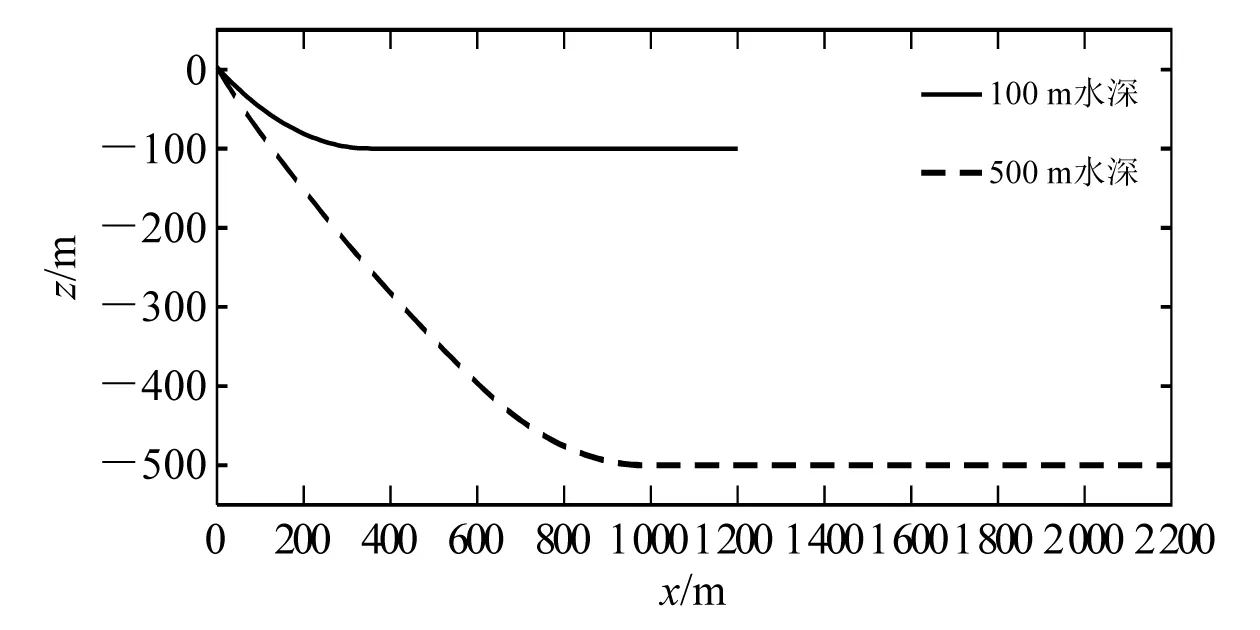
图3 系泊线构型
2.3 波浪条件
波浪为不规则波,采用JONSWAP谱,其参数如表3所示。由于在时域耦合分析过程中平台系泊系统的动力效应由波浪主导,仅研究极端波浪作用下的系统动力响应。

表3 波浪条件
3 系泊线张力陡增成因分析
3.1 系泊线张力陡增现象数值模拟
采用DeepC/Simo/Riflex软件进行浮体系泊系统时域耦合动力分析,在100 m和500 m水深某随机种子下得到的位移和张力时程曲线如图4和图5所示。由图4和图5可知:平台偏移和系泊线张力最大值均出现在6 600~6 800 s,而且在100 m 水深下出现显著的系泊线张力陡增现象。
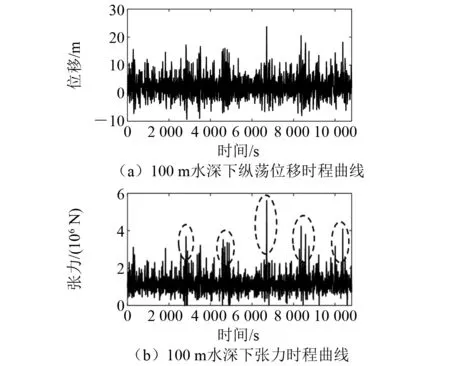
图4 100 m水深下平台偏移和系泊线张力时程曲线
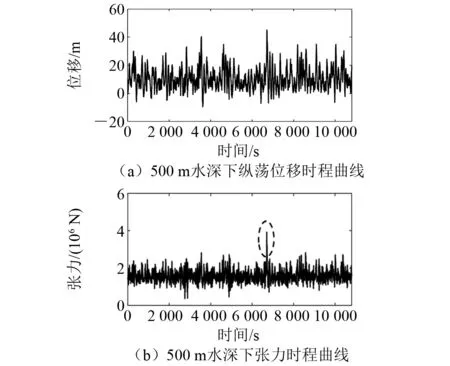
图5 500 m水深下平台偏移和系泊线张力时程曲线
表4给出5个随机种子结果的响应预报值。由表4可知,100 m水深下系泊线张力明显偏大,出现这一现象的原因可能如下:(1) 在浅水情况下波浪激励力较大;(2) 浅水悬链线系泊系统刚度大、几何非线性强,较小的位移即引起系泊系统几何特性较大的变化,使得系泊线容易进入张紧状态,产生较大的张力。

表4 2种水深下时域耦合分析结果响应预报
3.2 波浪力对张力陡增的影响
由时域耦合动力分析结果可知,在100 m水深下更容易出现系泊线张力陡增现象。为探究其原因,先对比2种水深下的波浪力结果。 图6为2种水深下平台纵荡运动方向一阶波浪激励力、平均波浪漂移力和二阶差频波浪激励力的频域水动力结果。由图6可知,2种水深下水动力参数整体相差较小:一阶波浪激励力在0.2~0.4 rad/s出现较小差异;二者平均波浪漂移力基本一致,仅在0.3 rad/s 附近有微小差异;二阶差频波浪激励力主要在0.2 rad/s≤(ω1,ω2)≤0.5 rad/s范围内有较小的差异。
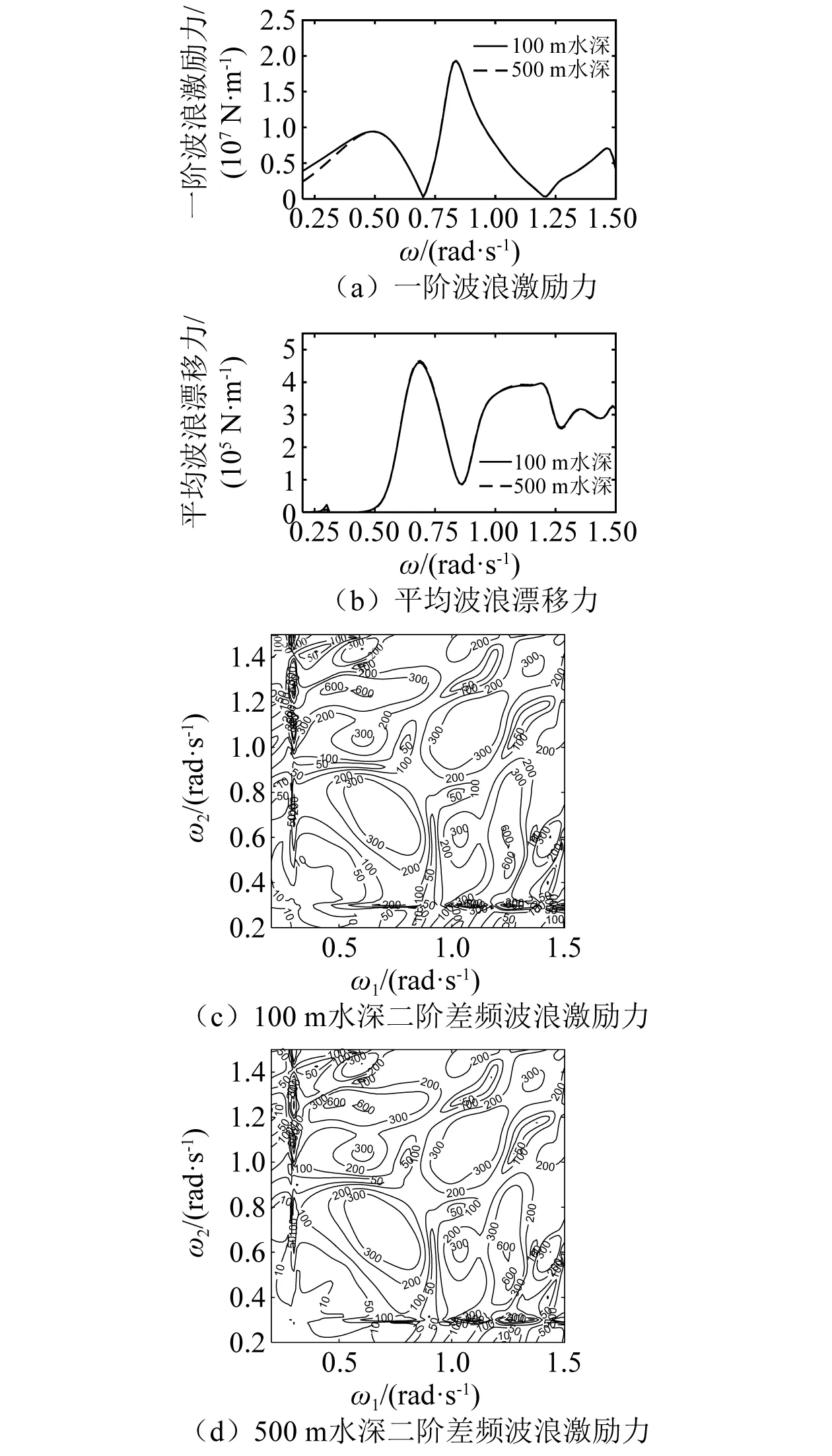
图6 2种水深下平台水动力参数对比
图7~图9给出了一阶、二阶波浪激励力的时程和能量谱,由图7和图8可知,2种水深的波浪激励力时程基本相同,而且一阶波浪激励力比二阶波浪激励力高一个数量级。由图9可知,2种水深下的波浪激励力谱几乎一致。上述结果可以说明,波浪激励力结果差异不是导致100 m水深下张力陡增现象显著的主要原因。
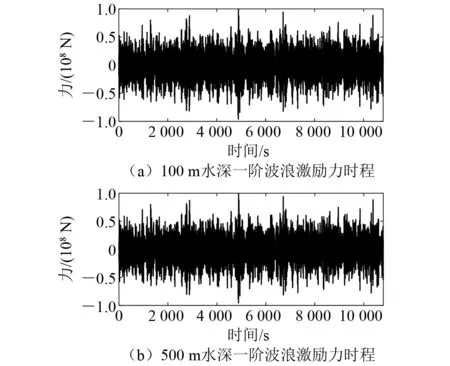
图7 2种水深下一阶波浪激励力时程
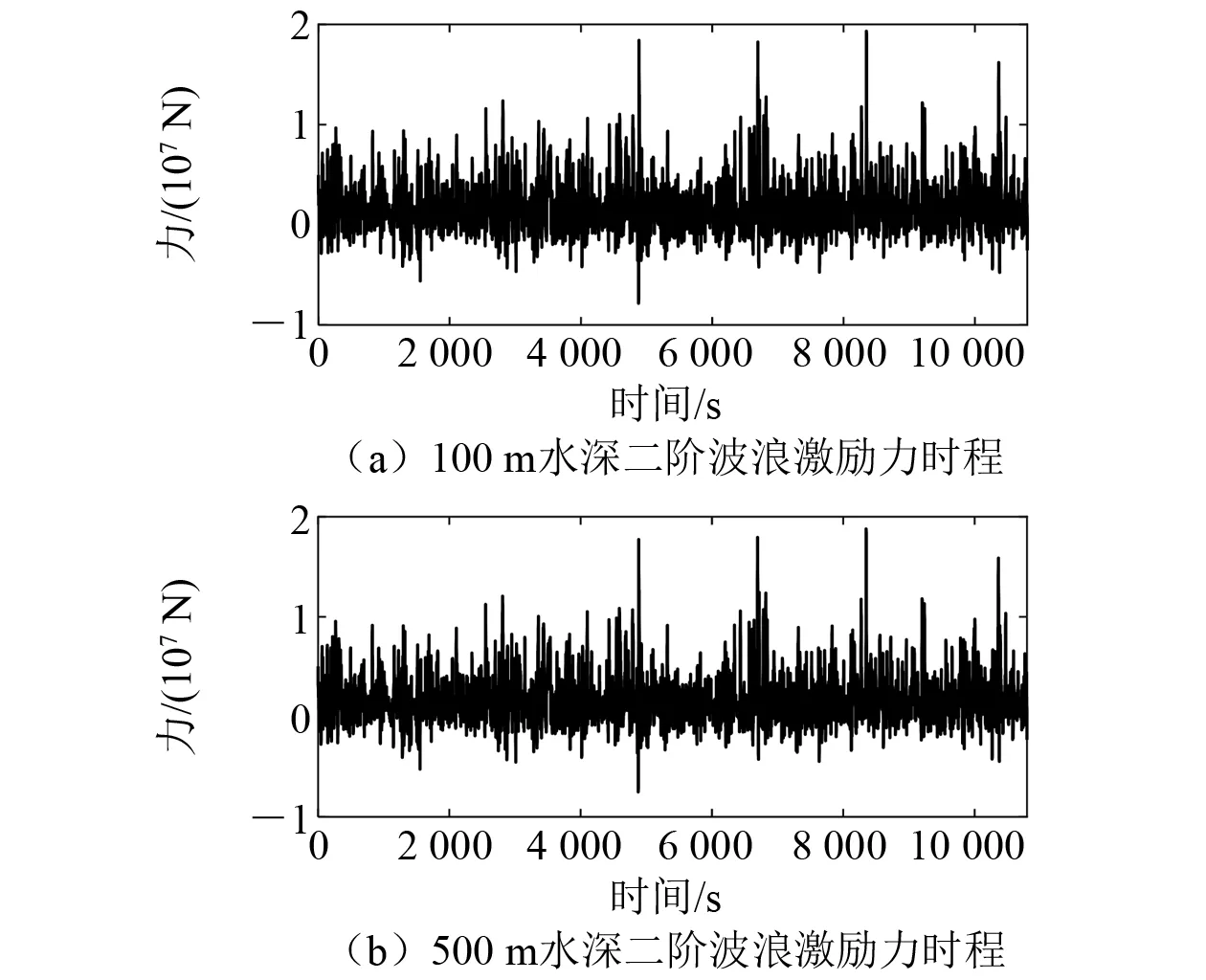
图8 2种水深下二阶波浪激励力时程
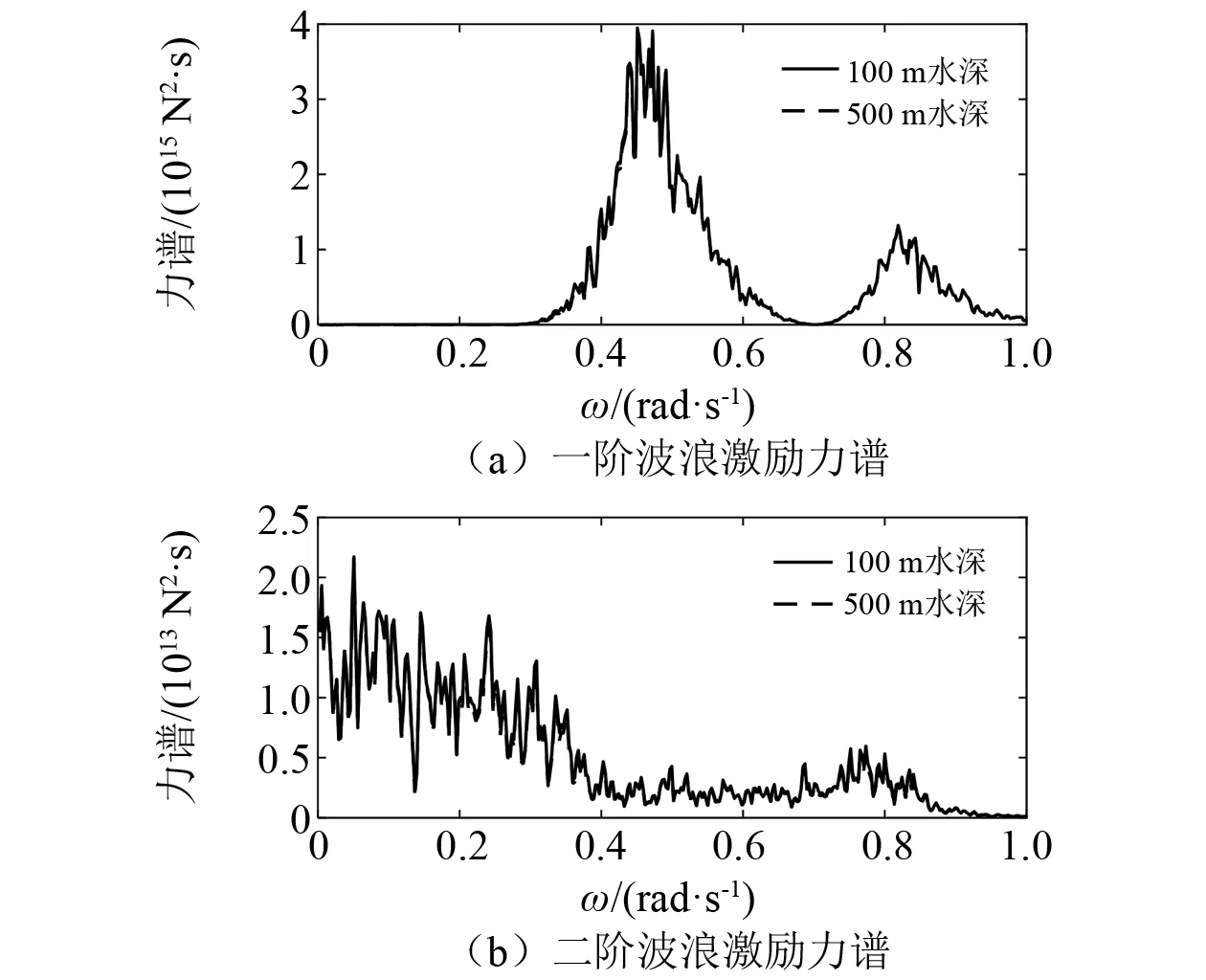
图9 2种水深下波浪激励力谱对比
3.3 系泊刚度对张力陡增的影响
为分析系泊刚度对张力陡增的影响,研究浅水和中等水深下的系泊系统刚度,以纵荡自由度为例,对所建立的半潜式平台/系泊系统施加一系列静载荷,得到系统位移-回复力曲线,即刚度曲线,如图10所示,可以发现,100 m水深下曲线更陡,系泊系统刚度更大,而刚度过大更容易使系泊线进入张紧状态,进而产生较大的张力。因此,在浅水情况下,系泊刚度过大及其强非线性特征是导致张力陡增现象出现的主要因素。
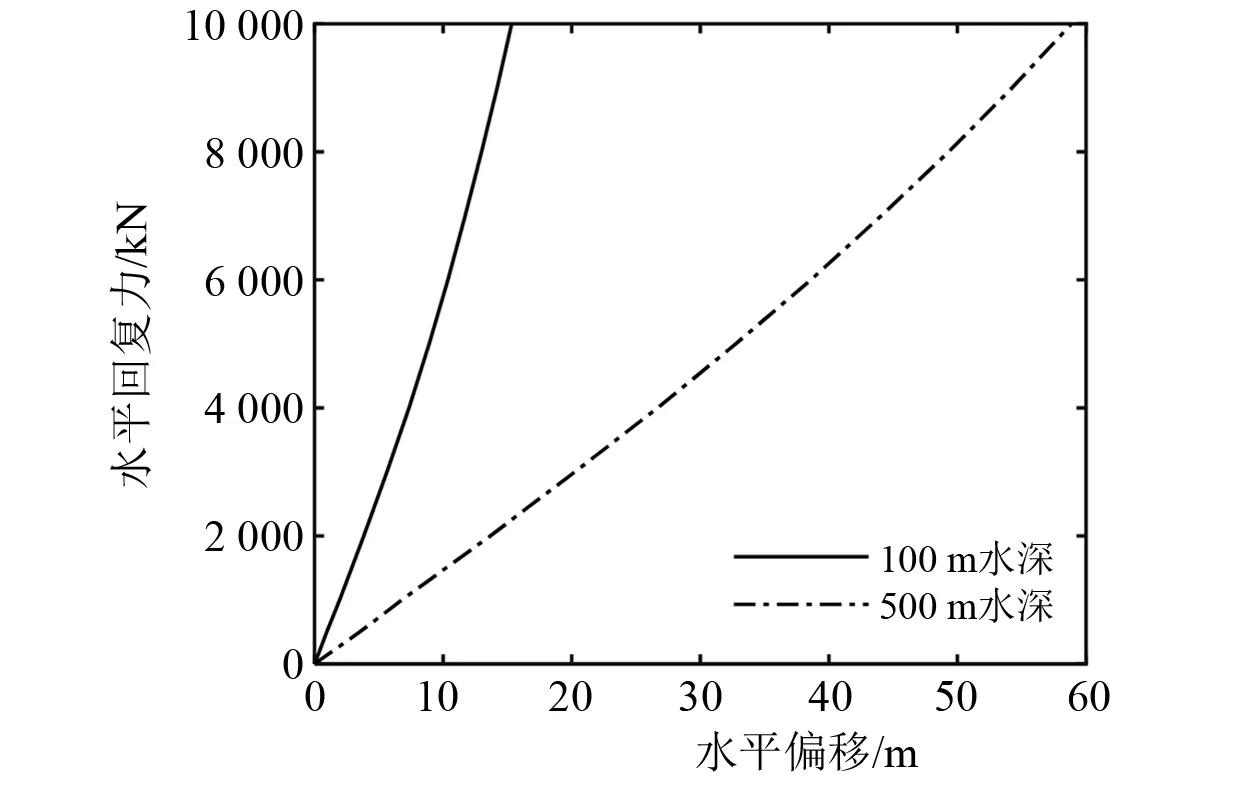
图10 2种水深下系泊系统位移-回复力曲线
4 浅水张力陡增应对方案研究及验证
2种水深下的波浪激励力相差较小,但系泊系统刚度有着显著差异,在浅水情况下,系泊刚度过大及其强非线性是导致张力陡增现象出现的主要原因。因此,从减小系泊线弹性刚度的角度出发,采取增加躺底段长度的措施,在同等水深下保持系泊线悬浮段长度和形态基本不变,进而使整体系泊系统刚度减小,以达到减小张力陡增幅值的目的,并以500 m水深情况作对比,分析增加躺底段长度的措施在中等水深是否仍能起到减小系泊线张力幅值的作用。计算工况如表5所示,图11给出了延长躺底段的示例。考虑到钢缆相较于锚链有更低的成本,工况9、10、11以工况2、3、4为基础,将躺底段延长部分用钢缆替换,替换长度分别为400 m、800 m、1 200 m,分析平台偏移和系泊线张力结果。
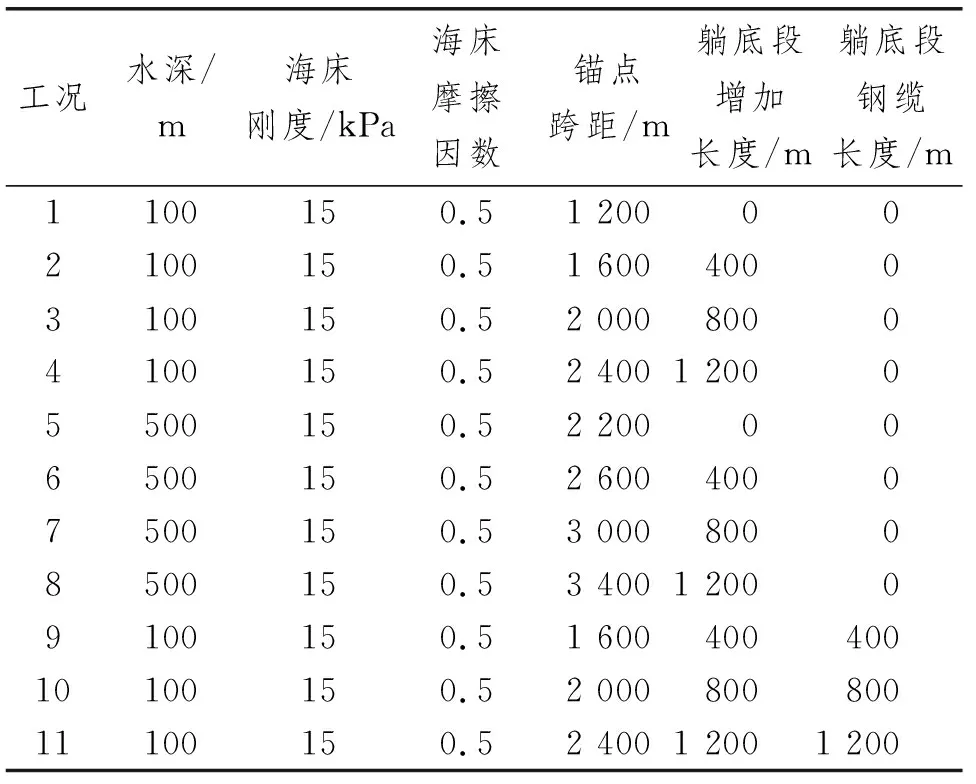
表5 系泊线躺底段长度影响计算工况
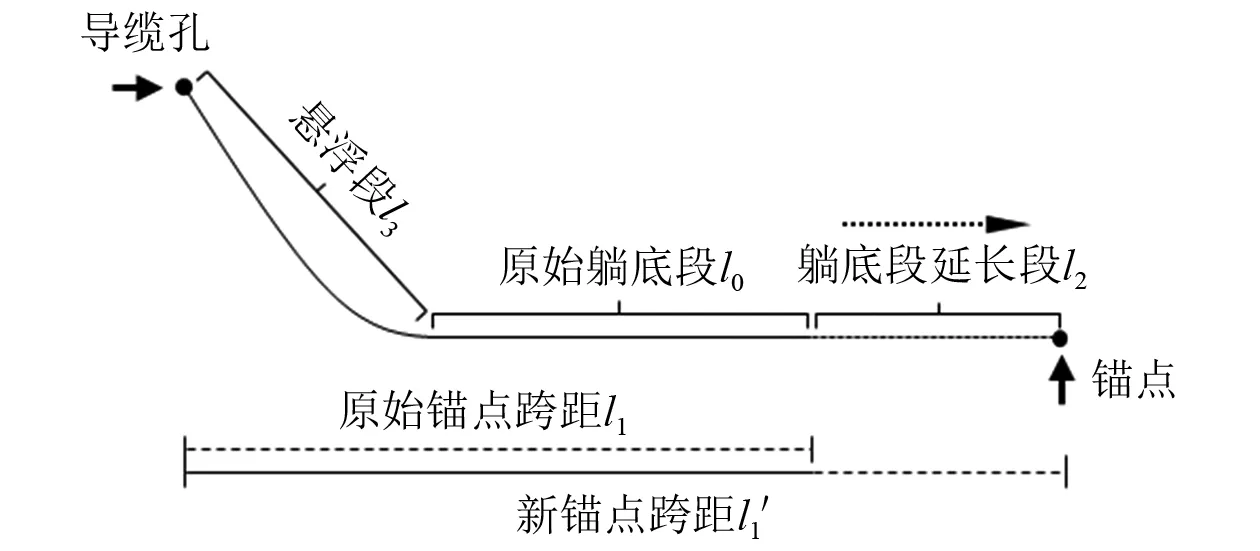
图11 系泊线躺底段延长示例
4.1 增加躺底段长度对位移-回复力曲线的影响
悬链线系泊系统的系泊刚度由几何刚度和弹性刚度组成,二者呈串联关系。当系泊线躺底段长度增加后,系泊线的弹性刚度减小,由于弹性刚度与几何刚度通过串联关系得到系统总刚度,因此系泊线躺底段长度增加会使系泊系统总刚度减小。位移-回复力曲线如图12所示(对应表5中工况1~工况8),可知:(1) 对于同一水深的系泊系统,随着躺底段长度增加,系泊刚度随之减小;(2) 当平台偏移距离较小时,系泊线躺底段长度变化对系泊系统刚度的影响较小,当平台偏移距离较大时,随着躺底段长度增加,系泊系统刚度显著降低;(3)随着躺底段长度增加,100 m水深下系泊刚度减小程度比500 m水深明显。
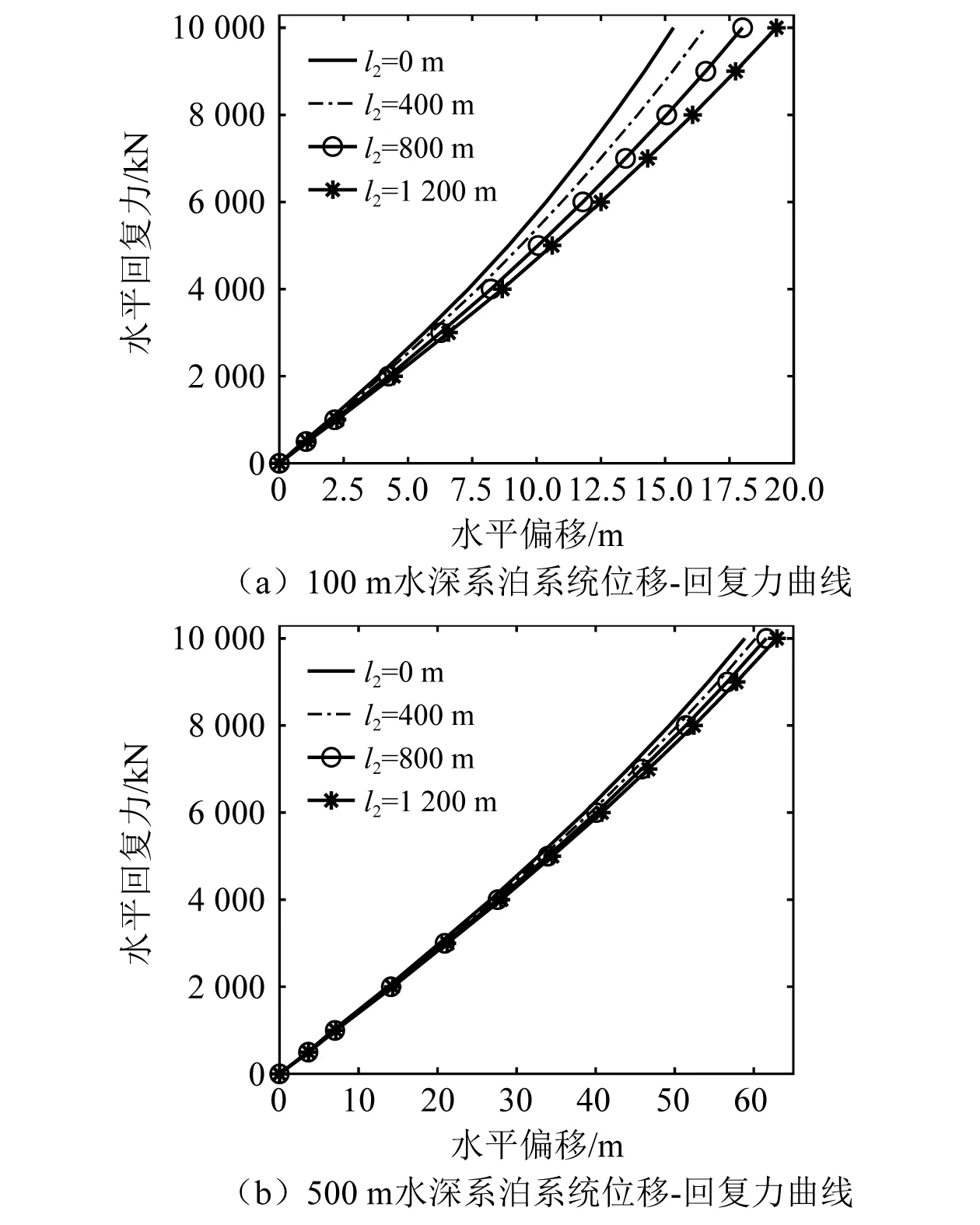
图12 2种水深下系泊系统位移-回复力曲线
4.2 躺底段长度变化对动力响应特征的影响
图13和图14分别对比100 m水深与500 m水深不同躺底段延伸长度下平台偏移和系泊线张力最大值附近的时程曲线,结果表明,随系泊线躺底段长度的增加,平台最大位移呈增大趋势,系泊线最大张力呈减小趋势,而且在100 m水深下更加显著。在浅水情况下,对系泊系统几何刚度产生贡献的悬链线效应较弱,使得系统弹性刚度占比增加,弹性刚度的变化对系统刚度的影响更加显著,而增加系泊线躺底段长度能够降低系泊线弹性刚度,因此在水深较浅的情况下,增加系泊线躺底段长度能更显著地降低系泊系统刚度,减小张力陡增幅值。
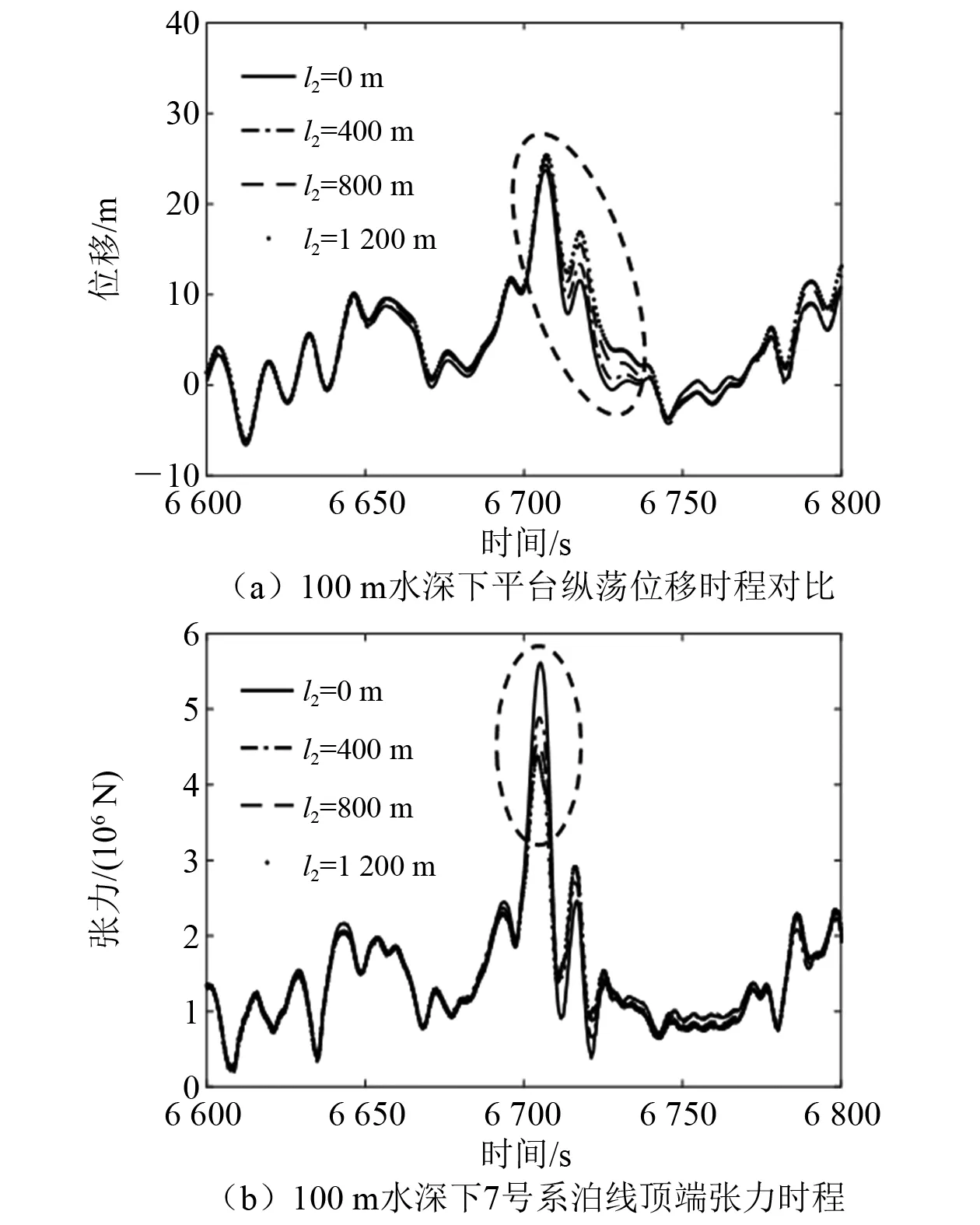
图13 100 m水深下平台偏移和系泊线张力时程曲线
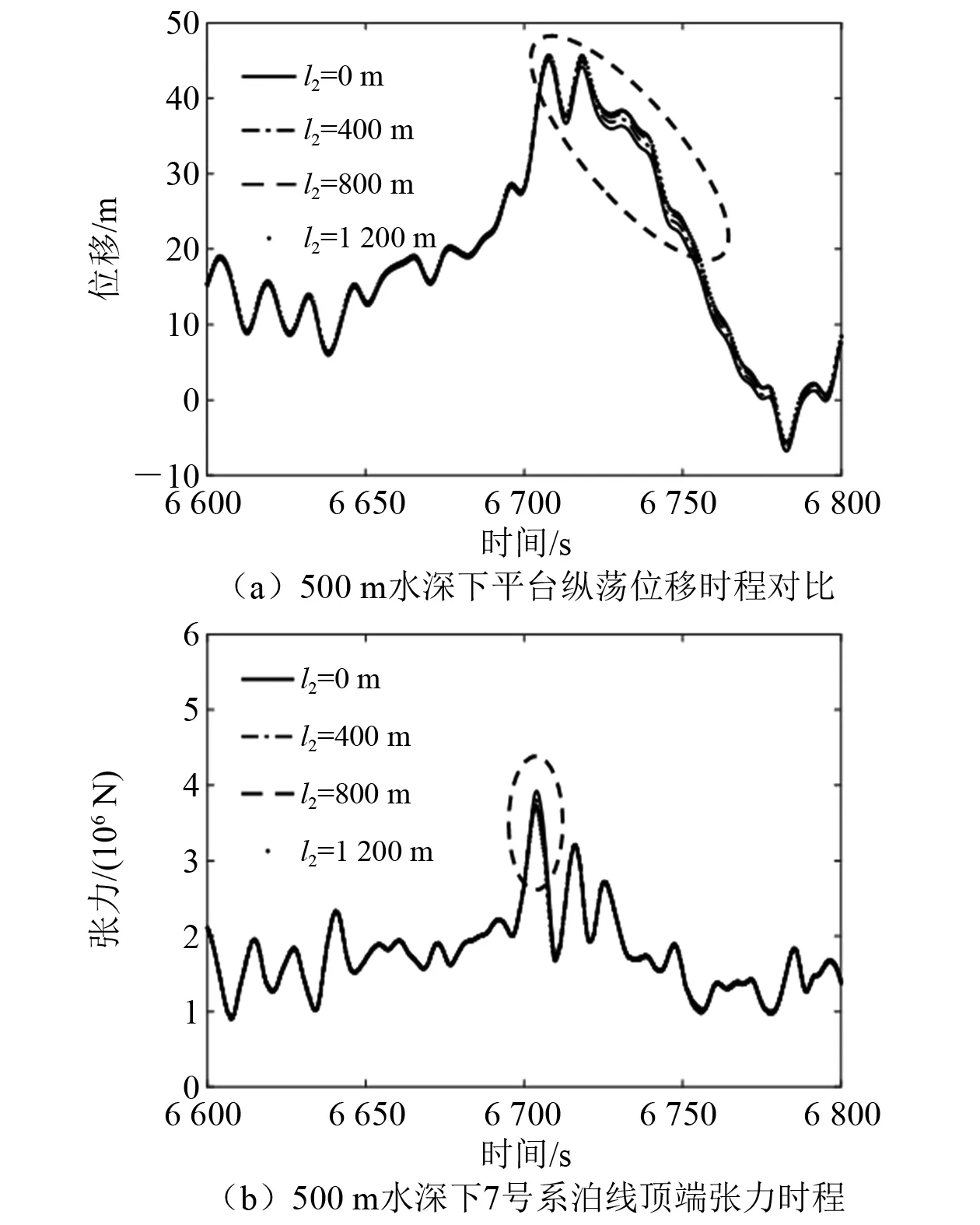
图14 500 m水深下平台偏移和系泊线张力时程曲线
图13和图14为某随机种子下的结果,能直观地给出系泊线躺底段长度变化对系统动力响应的影响。为进行定量分析,表6给出5个不同的随机种子下平台最大偏移和系泊线最大张力的响应预报值,2种水深分别以工况1和工况5为基准进行对比,结果表明:(1) 在100 m水深下,增加系泊线躺底段长度可有效减小最大张力幅值,当躺底段增加的长度达1 200 m时,最大张力可减小13.06%,此时平台偏移有所增加;(2) 在500 m水深下,增加系泊线躺底段长度仅能使最大张力幅值微幅减小,且对平台最大偏移的影响也较小。因此,通过增加系泊线躺底段长度来减小最大张力幅值的措施更适用于水深较浅的情况,但是需要综合考虑平台偏移和成本要求。
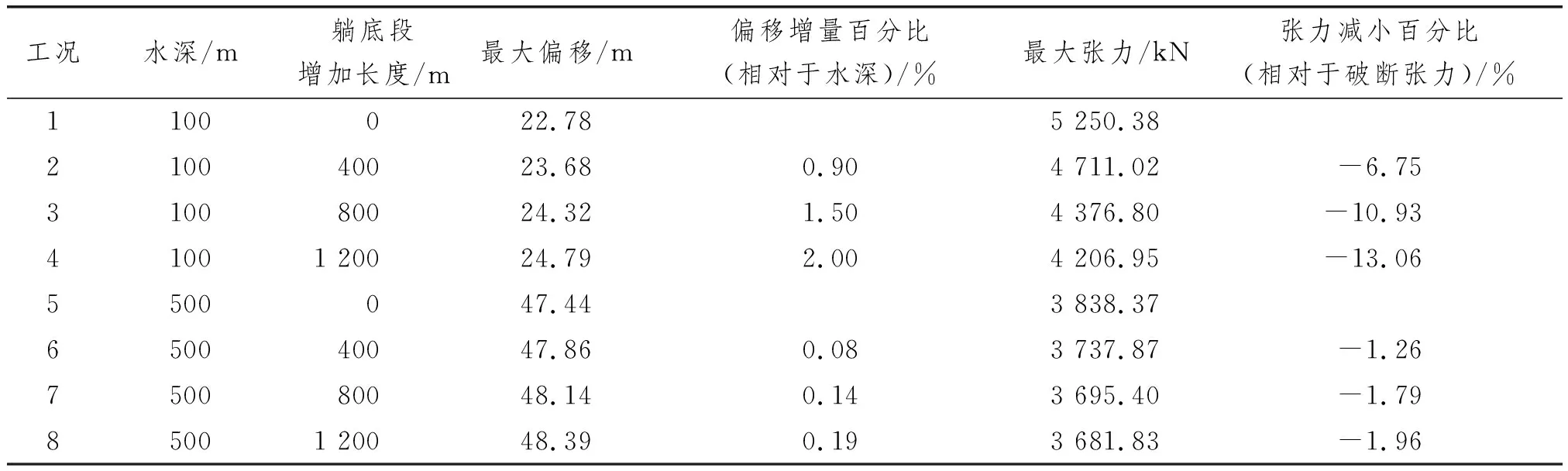
表6 不同躺底段长度下平台最大偏移和系泊线最大张力的响应预报值
4.3 躺底段部分替换为钢缆后系统动力响应特征
一般钢缆相较于锚链成本更低,考虑将躺底段延长部分用钢缆替换,平台最大偏移和系泊线最大张力的响应预报结果如表7所示,最大张力降幅百分比达11.99%。将躺底段延长部分用钢缆替换后同样具有降低系泊线张力幅值的效果,但是由于选用的钢缆轴向刚度大于锚链的轴向刚度,使得最大张力减小效果略有减弱,平台偏移的最大值增量也略有减小。因此,在采用增加系泊线躺底段长度来减小最大张力幅值的措施时,可以考虑用钢缆来延长躺底段以降低成本。

表7 躺底段用钢缆延长后平台最大偏移和系泊线最大张力响应预报
4.4 海床参数对系泊系统的影响
悬链线系泊有较长的躺底段,为了进一步研究海床对系泊系统的影响,针对100 m水深,以工况3的系泊系统布置为基础,考虑海床刚度和摩擦因数变化对系统动力响应特征的影响,计算得到的响应预报值如表8和表9所示。结果表明,海床刚度对平台最大水平偏移和系泊线最大张力的影响较小,最大影响程度分别为-0.03%和-0.13%,而海床摩擦因数增大会使平台最大水平偏移略微减小,使系泊线最大张力微幅增大,最大影响程度分别为-0.98%和1.15%。

表8 不同海床刚度下平台最大偏移和系泊线最大张力的响应预报

续表8 不同海床刚度下平台最大偏移和系泊线最大张力的响应预报
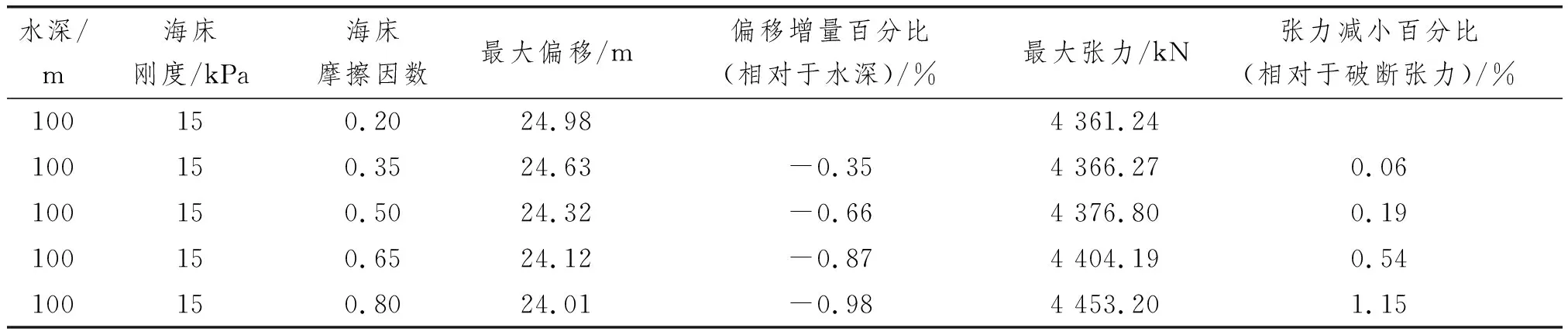
表9 不同海床摩擦因数下平台最大偏移和系泊线最大张力的响应预报
5 结 论
针对浅水条件下系泊刚度过大、在极端海况下出现系泊线张力陡增的问题,采用数值计算方法,研究系泊线张力陡增成因,分析2种水深下增加系泊线躺底段长度对平台最大水平偏移和系泊线最大张力的影响,考虑海床参数对系统响应特征的影响,得到如下结论:
(1) 100 m水深与500 m水深的波浪激励力相近,水动力随水深的变化不是张力陡增的主要原因;系泊线张力陡增主要由浅水系泊系统刚度大和强非线性导致。
(2) 增加系泊线躺底段长度能有效降低系泊系统刚度,在相同环境载荷作用下,使平台偏移微幅增大,但系泊线顶端张力大幅减小,而且这一现象在浅水情况下更加显著,说明在满足平台偏移要求的情况下,对于浅水悬链线系泊方式,通过增加系泊线躺底段长度来降低系泊线张力陡增幅值是有效可行的。为降低成本,可以采用钢缆延长系泊线躺底段。
(3) 对于采用线弹性地基模型的悬链线系泊系统:海床刚度对平台偏移和系泊线顶端张力的影响较小;海床摩擦因数增大会使平台最大偏移微幅减小,使系泊线顶端最大张力微幅增大。
