基于整机经济性的拖拉机HMCVT目标速比优化及控制仿真

黄薛凯,鲁植雄,陈雷,钱进,安宇辉

(南京农业大学工学院,江苏 南京 210031)

拖拉机田间作业时工况复杂,需要变速箱改变传动比,扩大发动机转矩转速的变化范围能适应经常变化的工作条件,同时也能使发动机在低油耗高功率的情况下工作。液压机械无级变速箱(hydro-mechanical continuously variable transmission,HMCVT)将发动机输入的功率进行分流,一路通过固定的齿轮传动,另一路通过泵控马达系统,利用行星排将2股功率进行汇流,通过结合不同的离合器实现不同段位的动力输出,是一种综合机械传动高效率与液压传动连续可调的变速箱[1-2]。

国内外学者对于无级变速箱的控制策略展开了相应的研究。Ahn等[3]针对变速箱效率在不同传动比下变化较大的情况,根据车辆需求功率反推发动机实际输出功率,建立了发动机与变速箱的最优经济性工作曲线。Lee等[4]考虑动力传动系统的响应延迟,提出一种新型速比优化算法实现对目标速比的修正,有效提高整机的燃油经济性。陆丽玲等[5]根据发动机万有特性曲线,制定了发动机最佳经济性、动力性速比,提出以发动机转速与变量泵排量比为控制量的控制策略。朱镇[6]针对基于发动机经济性、动力性的目标速比无法体现驾驶员操作意图的问题,运用加权的方法建立动力性与经济性综合的速比。张明柱等[7]以发动机转速、工作段位和实际速比作为控制参数,提出整机效率最大的HMCVT控制策略。滑杨莹[8]提出综合考虑考虑变速箱传动效率,建立以系统压力与车速为变量的最佳动力性速比。

本文在前人的研究基础上,综合考虑传动系统功率损失与速比的响应波动,对装备HMCVT的拖拉机整机的经济性进行研究。运用响应面法建立泵控马达系统效率的多项式回归模型,运用液压功率分流比的思想建立HMCVT传动效率模型。提出了整机经济性最佳的目标函数,设计了基于粒子群算法的遍历寻优算法,优化出任意车速与负载下的最优速比、发动机最优转速转矩,最后建立模糊PID控制器实现对目标速比的控制,通过仿真验证整机经济性最佳的控制策略的可行性。

1 HMCVT方案原理

液压机械无级变速箱的传动原理如图1所示,主要由变量泵控定量马达系统、行星排汇流机构与湿式离合器组成,具有3个前进液压机械段与3个倒退液压机械段。变速箱工作时,发动机功率一路直接流入P1行星排的齿圈,另一路经过定轴齿轮副i1流入泵控马达系统,调节变量泵的排量比改变马达的输出转速后,经齿轮副i2输出至P1行星排的太阳轮,结合不同的离合器实现不同段位的动力输出,利用变量泵排量的连续可调实现变速箱转速的连续变化[9]。

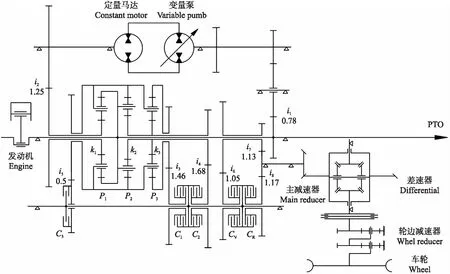
图1 液压机械无级变速器(HMCVT)传动原理图Fig.1 Hydro-mechanical continuously variable transmission(HMCVT)transmission diagram C1—C3为各段离合器;CV、CR为前进、倒退离合器;i1—i8为各齿轮副传动比;P1—P3为行星排;k1—k3为各行星排特性参数。C1-C3 represent wet clutches;CV and CR represent forward and reverse clutches;i1-i8 represent ratios of each gear pair;P1-P3 represent planetary rows;k1-k8 represent characteristic parameters of the planetary rows.

2 拖拉机整机经济性影响因素研究

2.1 拖拉机整机经济性评价指标

发动机的经济性评价指标是发动机燃油消耗率,通常以输出单位千瓦时有效功所消耗的燃料克数来表示,即发动机输出单位功率消耗的燃油量,如式(1)所示。

(1)

式中:ge为发动机燃油消耗率[g·(kW·h)-1];Be为耗油量(kg·h-1);Pe为发动机的输出功率(kW)。

以LR6105ZWT3型柴油发动机为研究对象,额定转速为2 200 r·min-1,额定功率为132 kW,参照文献[10]中的发动机试验数据进行多项式拟合[11],结果如图2所示,在不同的转速、转矩下发动机的燃油消耗率存在很大的差异。

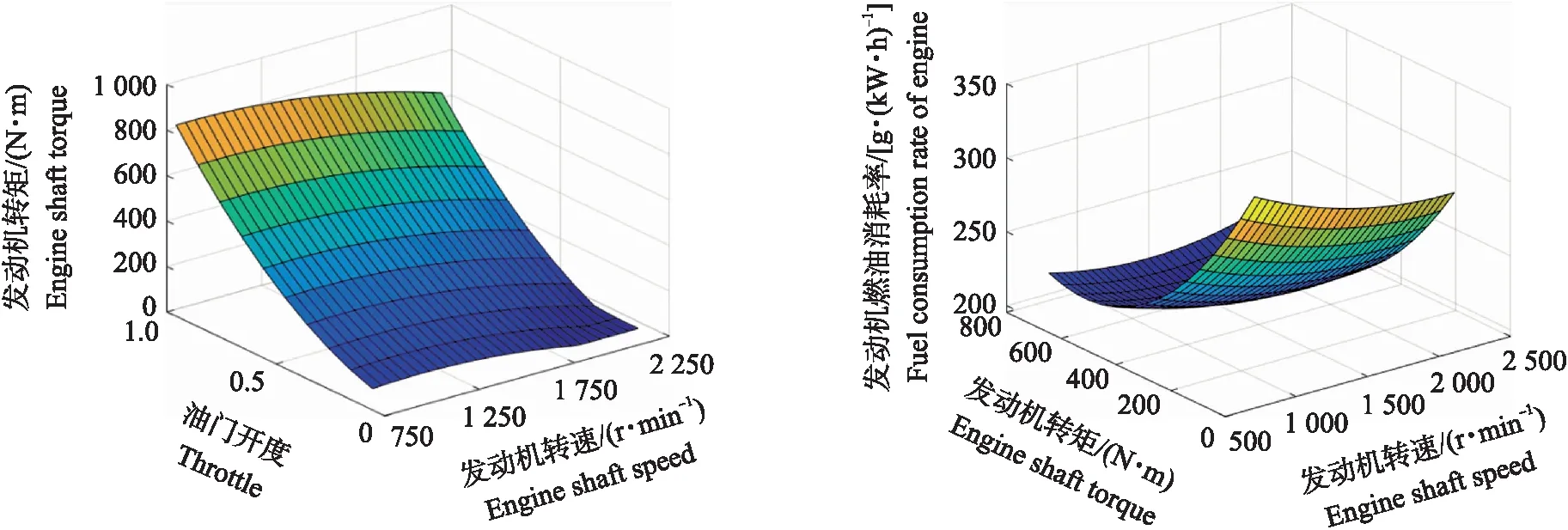
图2 发动机转矩输出与燃油消耗率模型Fig.2 Engine torque and fuel consumption rate model

拖拉机的经济性评价指标为拖拉机每小时耗油量BT(与发动机每小时耗油量相等)和拖拉机燃油消耗率gT,其中拖拉机燃油消耗率是指拖拉机在田间作业时在单位时间内完成单位工作量所消耗的燃油量。拖拉机在田间进行牵引作业时,可用牵引功率PT表示拖拉机的作业量,得:

(2)

式中:gT为拖拉机燃油消耗率[g·(kW·h)-1];BT为拖拉机耗油量(kg·h-1)。

上述分析可得拖拉机整机的经济性并不等于发动机的经济性,发动机输出的动力经过动力传动系统驱动车辆前进并进行牵引作业,在传动过程中必然存在着功率的损失,发动机输出功率并不等于拖拉机作业时的牵引功率,因此必须从整机出发来评价拖拉机的经济性。

2.2 影响拖拉机经济性的因素

发动机输出的动力经过变速箱、主减速器、轮边减速器后转化为驱动力,克服地面阻力以及牵引阻力进行牵引作业[12-13],根据传动路线得:

(3)

(4)

式中:ηT为传动系统的总效率;Pq为驱动功率(kW);ηb为变速箱效率;ηz中央传动效率;ηδ为滑转效率;ηf为滚动效率。

HMCVT包括液压与机械双流传动,传动效率受到负载转矩、传动比以及输入转速等多种因素的影响,在不同的工况下效率值存在较大的差别,因此不能将HMCVT的传动效率简单地认为是一个定值。

中央传动包括主减速器与轮边减速器,传动效率一般可认为是定值。车辆滚动效率与车辆自身质量、滚动阻力系数以及牵引阻力有关,如式(5)所示。滑转效率取决于地面与负载,视为车速的损失,在固定工况下无法通过调节变速箱传动比与发动机工作点进行改变,在下文的研究中取定值,如式(6)所示。

(5)

(6)

式中:Ff为滚动阻力(N);FT为牵引阻力(N);G为拖拉机自重(N);μ为滚动阻力系数;δ为滑转率;vr为实际车速;va为目标车速;Fq为驱动力(N)。

拖拉机在固定工况下进行作业时,地面与牵引负载不变,滚动效率、滑转效率以及中央传动效率都是定值,只有调节变速箱的传动比与发动机的工作点才能改变HMCVT的效率,实现整机燃油消耗率的最小化,变速箱传动效率对于整机经济性最佳速比的制定尤为重要。

3 目标速比的优化

3.1 HMCVT传动效率

HMCVT在工作时,液压路与机械路分别传递功率,液压路采用的是变量泵控定量马达系统,机械路是行星排与定轴齿轮副传动。为提高液压路效率模型的精度,运用泵控马达试验台架进行效率试验,对泵马达系统整体效率进行拟合。图3所示为泵马达试验台架,由发动机、转速转矩传感器、装有泵马达的变速箱以及电涡流测功机组成,上位机系统采用LABVIEW软件搭建监控界面。台架采用林德HPV55-02变量泵,最大排量55 cm3·r-1,最大连续工作转速3 700 r·min-1,最大工作压力420 bar;马达采用林德HMF55-02定量马达,额定排量为55 cm3·r-1,最大连续工作转速为4 400 r·min-1,最大工作压力420 bar。

图3 泵马达试验台Fig.3 Pump motor test bench 1. 液压控制台 Hydraulic console;2. 发动机 Engine;3、5. 转速、转矩传感器 Speed and torque sensor;4. 变速箱箱体 Transmission case;6. 电涡流测功机 Eddy current dynamometer;7. 转速转矩功率采集仪 Speed torque power collector;8. 电源 Power;9. 工控机 Industrial computer;10. 开关 Switch;11. 踏板 Accelerator pedal.

确定影响泵控马达系统效率的主要因素为系统输入转速、马达轴转矩与变量泵排量比,范围分别是500～3 000 r·min-1,50～500 N·m,0.17～1.00,其中正排量与负排量等效只是工作方向不同,因此只对正排量进行试验[14-16]。设计中心复合试验,在因子空间选择中心点、二水平析因点以及轴点这三类具有代表性的点,运用正交原理进行组合,利用较少的试验次数得到高精度的回归方程,因素水平编码如表1所示。

表1 效率试验因素水平Table 1 Factors and levels of efficiency test

试验时首先打开控制台电源,在上位机界面中输入变量泵的排量比,调节上位机界面的电流,控制测功机的负载进而调节马达轴的转矩,最后旋动踏板上的螺钉调节泵马达试验台的输入转速,根据试验台输入与输出的转速转矩传感器数据计算当前效率。按照试验方案进行20组试验,每组进行10次重复试验取平均值,试验结果如表2所示。

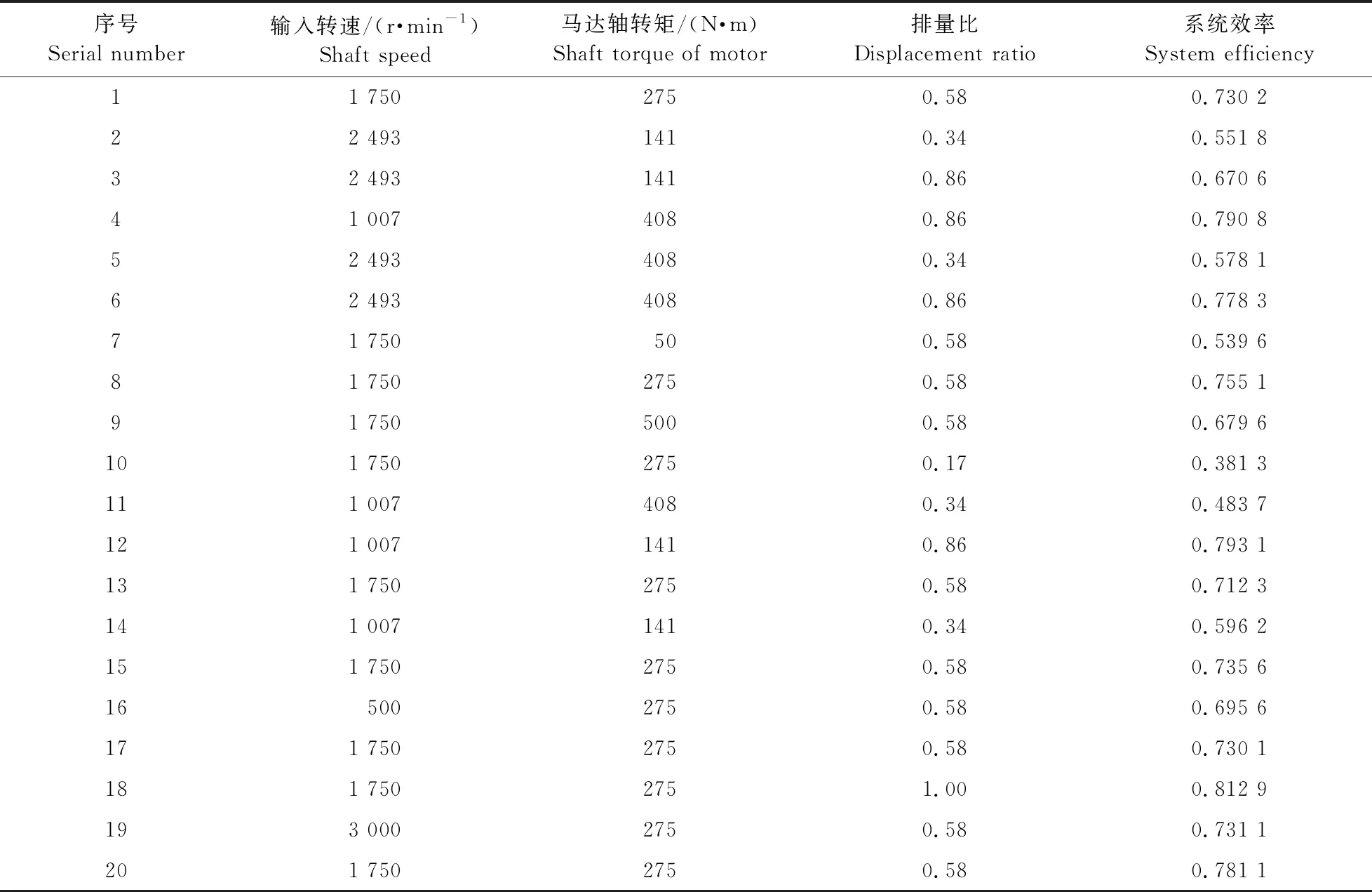
表2 效率试验数据Table 2 Data of efficiency test

运用响应面分析法对获取的效率试验数据进行处理,根据样本值构造多项式逼近函数,通过试验数据确定逼近函数的待定系数,进而建立泵控马达系统效率模型[17]。选用二次多项式作为响应面回归方程,建立以泵控马达系统效率为响应,变量泵排量比、马达轴转矩与系统输入转速为变量的回归方程,零水平下响应曲面如图4所示。从响应曲面分析可得排量比一定时,系统效率在中低转速、中高转矩下处于较高区域;马达轴转矩一定时,系统效率在中高排量比以及中低转速下处于较高区域;转速一定时,系统效率在大排量、中高转矩下处于较高区域。

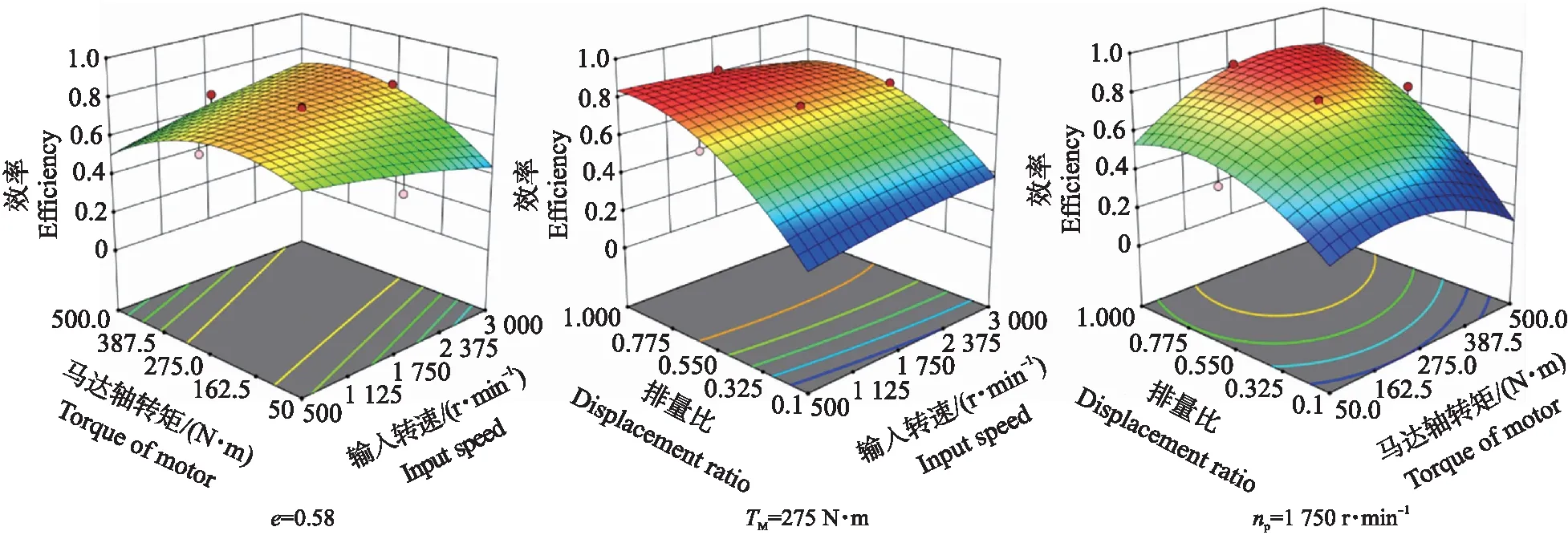
图4 液压系统传动效率Fig.4 Efficiency of hydraulic system

为计算HMCVT的整体传动效率,引入液压功率分流比的概念[18],即液压路传递的动力占整体输出动力的比值,如图5所示。液压路与机械路传递的功率分别乘液压与机械部分的传动效率便可计算得输出功率,进而计算HMCVT传动效率。对于定轴齿轮副传动效率取0.98,行星排功率损失系数取0.023,HMCVT传动效率如表3所示。

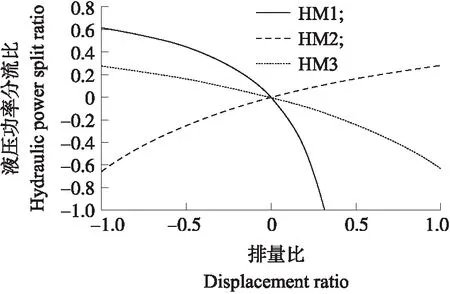
图5 液压功率分流比Fig.5 Hydraulic power split ratioHM1、HM2、HM3为HMCVT的3个工作段位。HM1,HM2 and HM3 are three working segments of HMCVT.

表3 HMCVT传动效率Table 3 Transmission efficiency of HMCVT

3.2 基于粒子群算法的速比优化

根据前文分析,在固定工况即牵引负载与目标车速一定的情况下,发动机燃油消耗率与HMCVT传动效率决定着拖拉机的经济性,参照文献[19]对于目标函数的设计,结合前文对于拖拉机经济性影响因素的分析,提出以下目标函数:

(7)

式中:ne为发动机转速(r·min-1);Tb为变速箱负载扭矩(N·m);ib为变速箱传动比。

牵引阻力与变速箱转矩以及拖拉机车速与发动机转速的关系如下:

(8)

(9)

式中:V为车速(km·h-1);rd为驱动轮半径(m)。

对于给定的地面负载以及目标车速,可以转换成变速箱负载转矩以及变速箱输出转速,目标函数可以看作是以变速箱负载转矩与变速箱输出转速为自变量,速比与发动机转速为优化变量。自变量的范围定为变速箱在当前段位内所能传递的最大、最小转矩转速。优化变量约束如下:

(10)

式中:ne为发动机输出转速(r·min-1);Te为发动机输出转矩(N·m);n为变速箱段位。

采用粒子群算法优化目标速比,优化变量可以当作搜索空间中的1个粒子,包含速度与位置2个特性,当前粒子的坐标作为适应度函数的评价,粒子通过跟踪个体最优解与当前全局最优解不断更新自己的位置。位置更新公式由3部分组成,分别是惯性部分、自身认知部分以及社会认知部分[20]。其中,惯性部分代表粒子保持前一时刻的速度大小和方向的影响;自身认知部分代表粒子逼近自身最佳位置的趋势,保证算法能够局部收敛;社会认知部分是一个从当前点指向种群最好点的矢量,反映粒子间的协同合作与知识共享。粒子位置、速度更新公式如下:

Vi+1=ωVi+C1rand1×(Pbesti-Xi)+C2rand2×(gbesti-Xi)

(11)

Xi+1=Xi+Vi

(12)

式中:ω为惯性因子;C1、C2为学习因子;rand1、rand2是0～1间的随机数;Pbesti为个体最优解;gbesti为全局最优解;xi为粒子位置;Vi为粒子速度;i为迭代次数。

惯性因子在较大时全局寻优能力较强,较小时局部寻优能力强,采用线性递减权值策略,对局部寻优性能和全局寻优性能进行调整,公式如下:

(13)

式中:Tmax表示最大迭代次数;t表示当前迭代次数;ωmin表示最小惯性权重;ωmax表示最大惯性权重。

设计基于粒子群算法的遍历寻优算法,优化出每一组变速箱输出转速与转矩对应的经济性目标速比以及发动机转速、转矩,计算流程如图6所示。

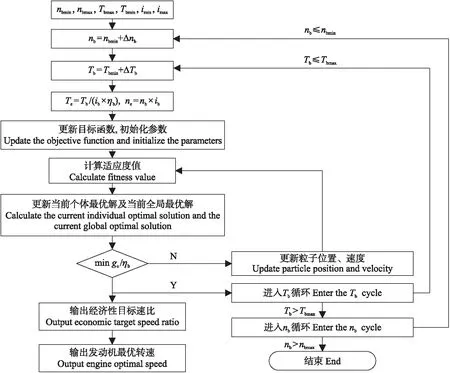
图6 基于粒子群算法的遍历寻优流程Fig.6 Traversal optimization process based on particle swarm optimization

拖拉机整机经济性最优的优化结果如图7所示。速比呈平台状分布,对应3个段位,在段位重叠区间算法优化出使目标函数更小的传动比。在高速低负载的工况下速比变化比较平稳,在低速大负载的情况下,速比变化比较大。为便于下文对拖拉机整机经济性的仿真验证,建立以发动机燃油消耗率为目标函数的发动机经济性最佳的目标速比、发动机转速、转矩三维图,如图8所示。两种经济性目标速比变化趋势相似,但是在低速大负载时,拖拉机整机经济性速比小于发动机经济性速比。

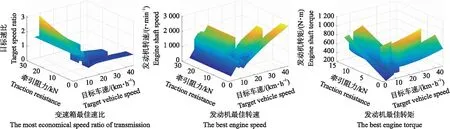
图7 整机经济性最佳的控制参数Fig.7 The control parameter of the best economical efficiency of the tractor

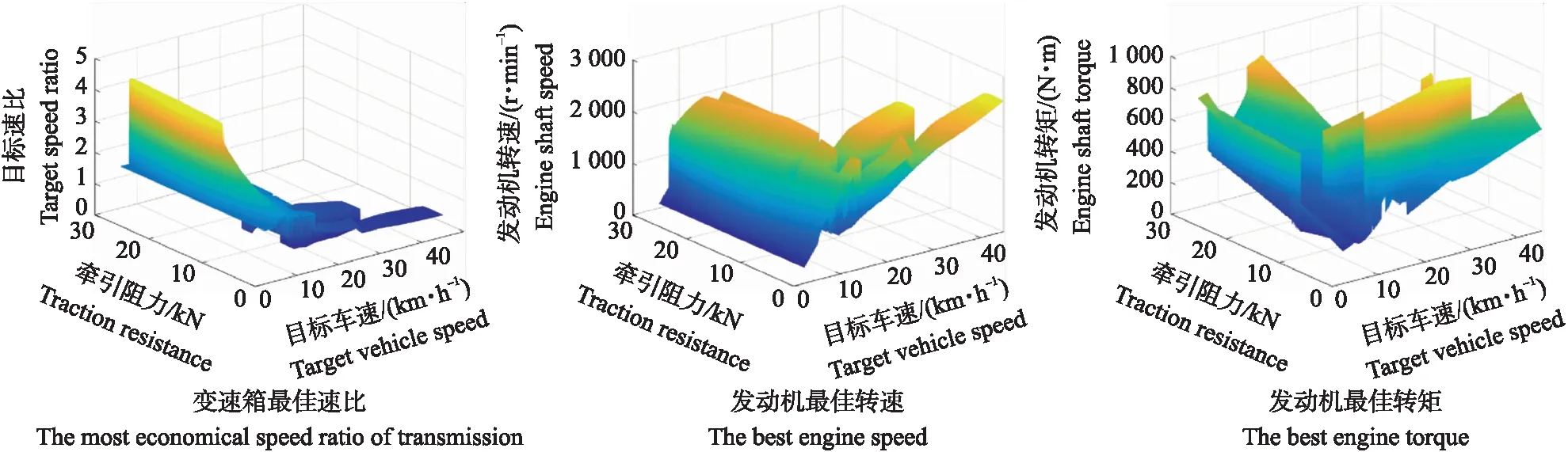
图8 发动机经济性最佳的控制参数Fig.8 The control parameter of the best economical efficiency of the engine

4 经济性控制策略的仿真分析

整机经济性最佳的控制策略如图9所示。以HMCVT的速比与发动机转速为控制参数,驾驶员设置目标车速,控制器接收目标车速与地面负载后,根据优化出的最优经济性控制参数输出变速箱目标速比与发动机目标转速,进而计算出变速箱的目标输出转速,通过控制变量泵的斜盘倾角调节定量马达的输出转速,实现对目标速比的响应[21]。

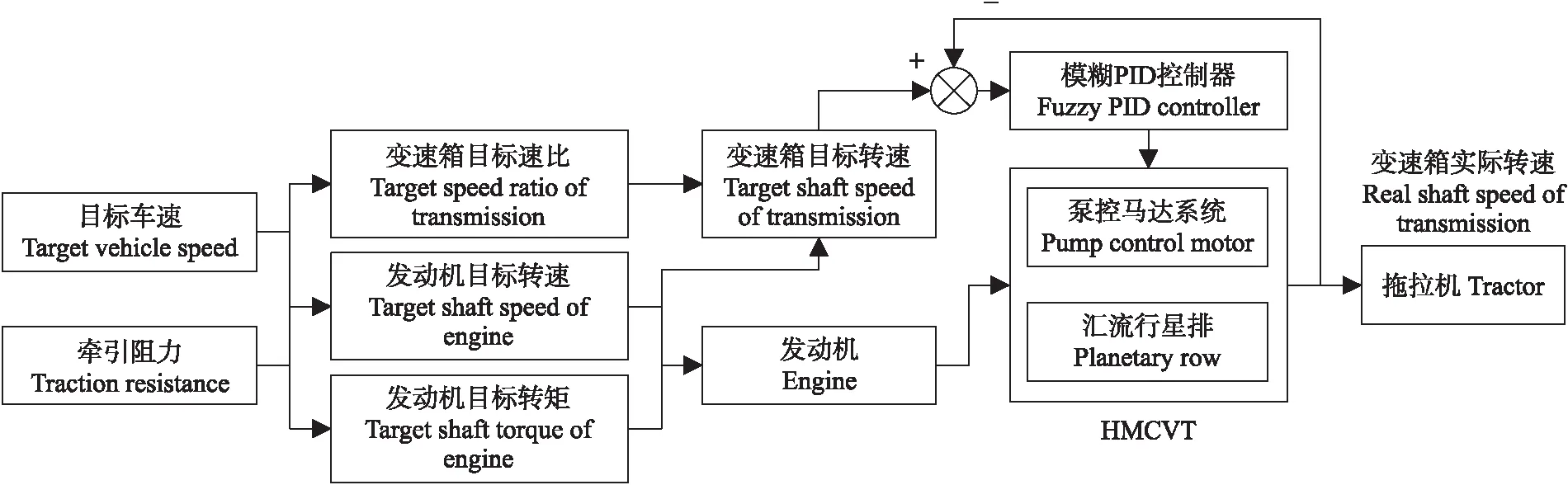
图9 整机经济性最佳的控制策略Fig.9 Control strategy with the best tractor economy

变速箱的泵控马达系统是一个高阶次非线性系统,存在着精度不高响应时间过长的问题,因此设计模糊PID控制器对变速箱进行控制,通过模糊规则输出一组PID参数的修正值,实现PID参数的实施修正。选择Mamdani型的模糊控制器,输入量为转速偏差e,偏差率ec,输出为Δkp、Δki、Δkd,论域分别取[-50,50],[-200,200],[-10,10],模糊集为{NB,NM,NS,ZO,PS,PM,PB},代表{负大,负中,负小,零,正小,正中,正大},模糊论域均为{-6,6}。采用三角形隶属度函数作为输出量的隶属度函数,利用三角形隶属度敏锐度高的特点提高控制效果[22]。模糊规则与参数输出曲面如图10所示。

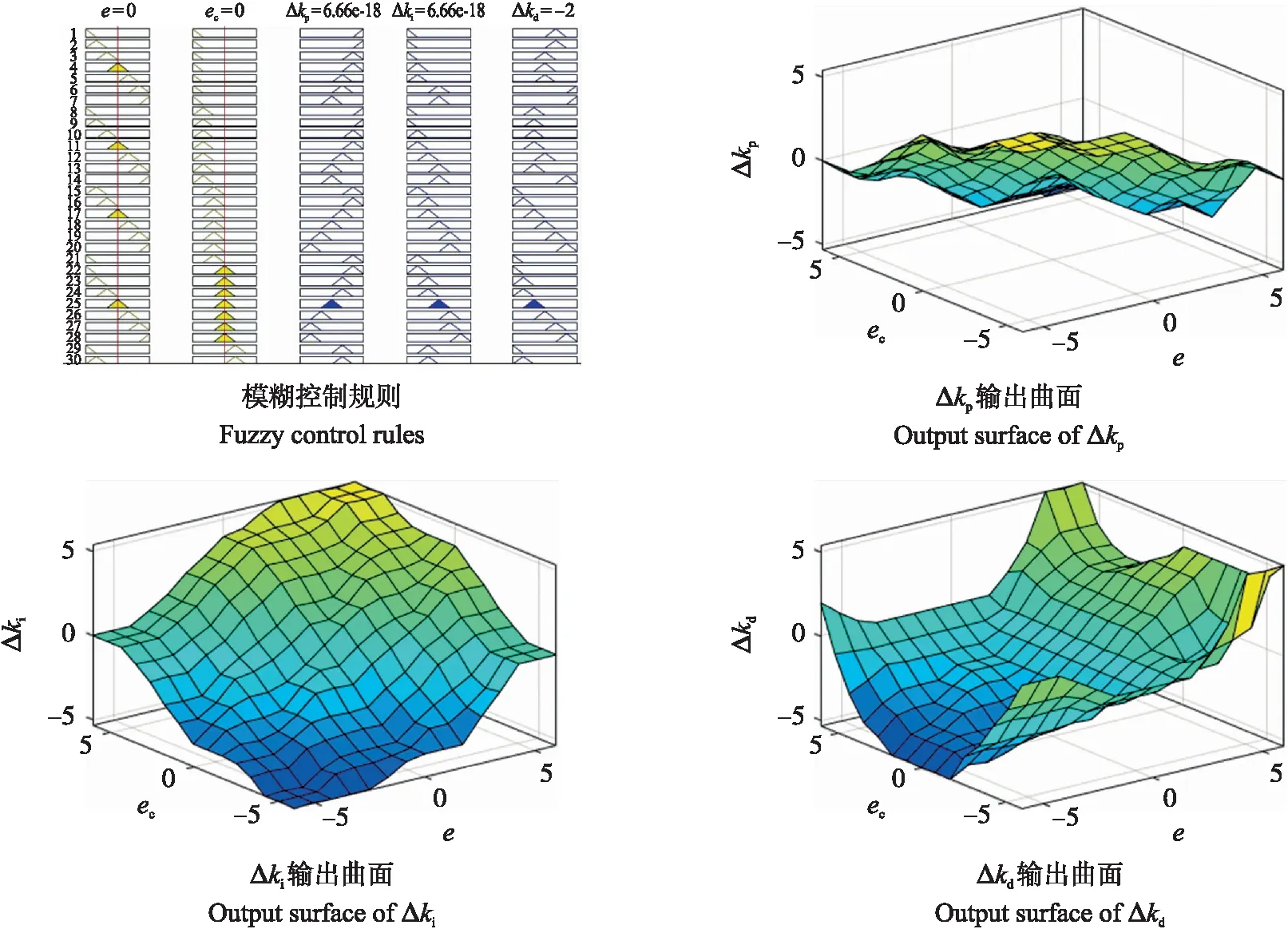
图10 模糊控制规则与输出曲面Fig.10 Fuzzy control rules and output surfaces

整机经济性最佳的仿真模型如图11所示,主要包括发动机模块、速比模块、效率模块、HMCVT模块以及负载模块[23]。仿真主要参数为:拖拉机整机质量7 500 kg,驱动轮半径0.9 m,主减速比3.8,轮边减速比7.07,滚动阻力系数0.12。通过临界比例法诊定PID参数为2.5、3、1。传动系统动力学方程与传递函数如下式所示:

(14)

(15)

(16)

式中:Je为发动机转动惯量(kg·m2);Td为变速箱输出轴等效阻力矩(N·m);Jω为驱动轮等效转动惯量(kg·m2);kp为变量泵流量增益;Dm为马达排量(cm3·r-1);ωn为液压固有频率(Hz);ξn为液压阻尼比;we为发动机角速度(rad·s-1);ib为变速箱传动比;V为拖拉机车速(m·s-1)。

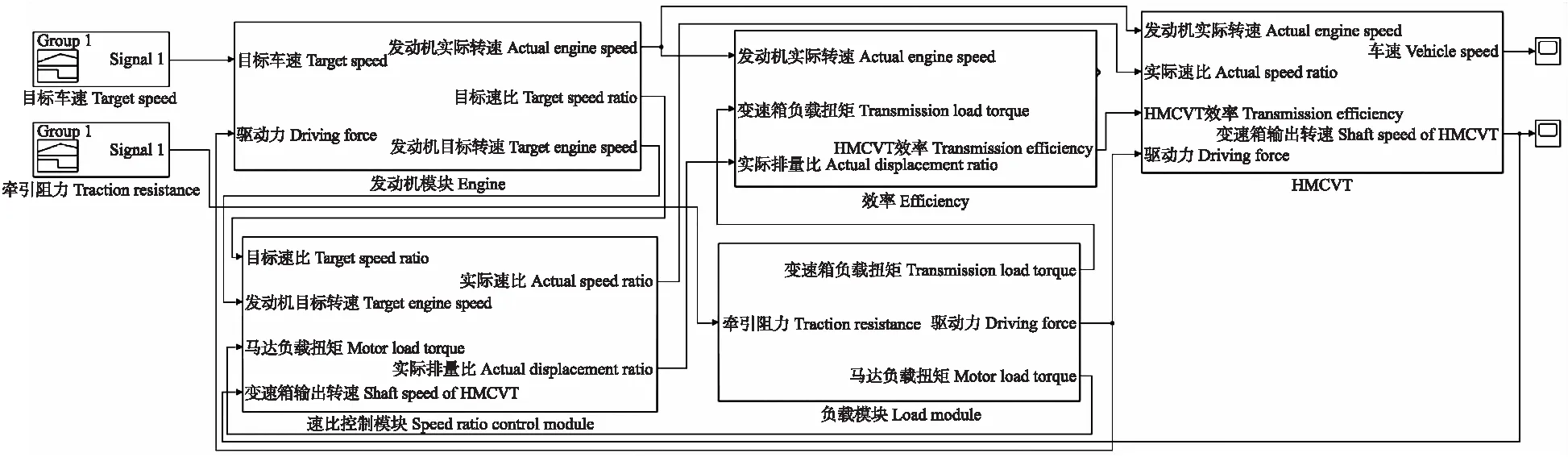
图11 整机经济性最佳的HMCVT仿真模型Fig.11 Simulation model with the best vehicle economy of HMCVT

拖拉机在田间作业时车速通常为5～15 km·h-1,仿真设置5 s时牵引负载由5 kN变为10 kN,目标车速不变为10 km·h-1。在10 s时,牵引负载保持不变为10 kN,目标车速由10 km·h-1变为5 km·h-1。分别模拟拖拉机在田间的正常作业、作业阻力突变以及作业时车速改变的情况,仿真结果如图12所示。

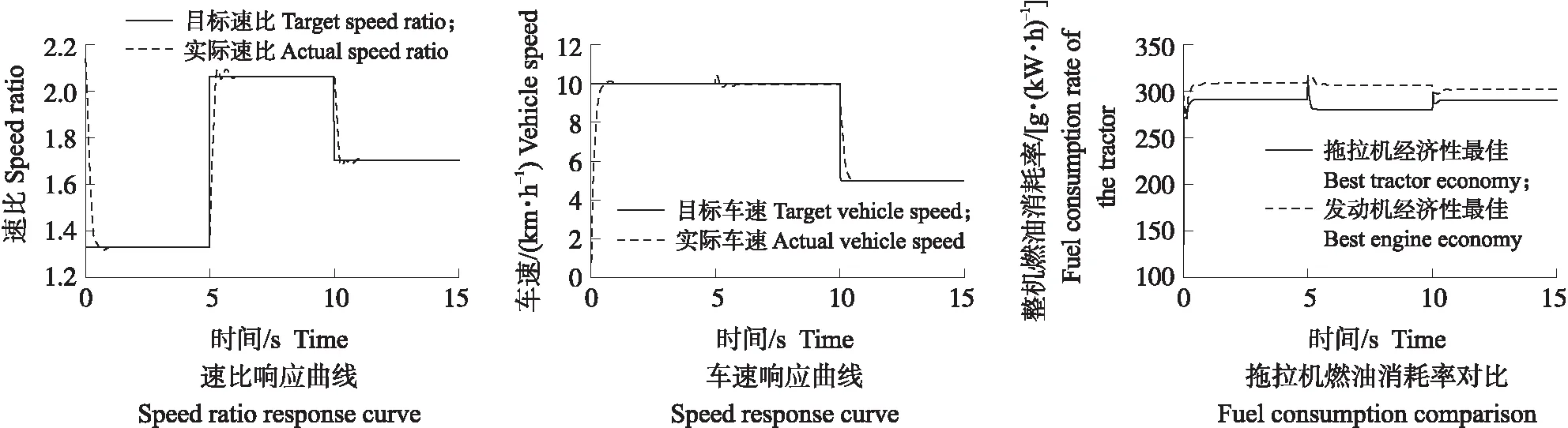
图12 整机最佳经济性控制策略仿真结果Fig.12 Simulation results of the optimal economic control strategy

在5 s时负载突变,系统最大超调量为1.41%,调节时间为1.143 s,在短暂的震荡后,拖拉机又恢复 10 km·h-1的速度进行作业。在10 s时目标车速由10 km·h-1变为5 km·h-1,系统最大超调量为1.23%,系统调节时间为1.08 s,拖拉机能稳定在新的目标车速。仿真表明模糊PID控制器能够实现对目标速比的跟踪,拖拉机能稳定在目标车速上。采用整机经济性最佳控制策略的拖拉机相对于常规基于发动机经济性最佳的拖拉机,在3种工况下整机燃油消耗率分别降低了5.73%、9.36%、3.97%,显著提高了拖拉机的经济性,提出的整机经济性最佳的控制策略具有可行性。

5 结论

1)分析发动机燃油经济性与整机燃油经济性的区别,提出影响拖拉机经济性的因素。设计了中心复合试验,对泵控马达系统进行效率试验,运用响应面法建立了泵控马达系统效率的回归方程,运用液压功率分流比法建立HMCVT的效率模型。

2)提出以发动机燃油消耗率与HMCVT效率之比最小作为目标函数,以拖拉机牵引阻力与拖拉机车速为自变量,变速箱速比与发动机转矩、转速为优化变量,运用粒子群算法进行遍历寻优,优化出整机经济性最佳的目标速比与发动机转速、转矩。

3)提出了整机经济性最佳的控制策略,以发动机转速与HMCVT速比为控制参数。建立了整机动力学模型,通过仿真验证了整机经济性控制策略的可行性。仿真结果显示模糊PID控制器可以实现速比的有效控制,拖拉机能稳定在目标车速上工作,采用整机经济性最佳的速比可以有效降低拖拉机的燃油消耗率,研究结果为装有HMCVT的拖拉机的智能化控制提供了理论参考。