应用CFD方法的舰载直升机舰面气弹响应计算与分析

2022-08-11张冉徐国华史勇杰王清

航空工程进展 2022年4期

张冉，徐国华，史勇杰，王清

（1.南京航空航天大学直升机旋翼动力学国家级重点实验室，南京 210016）

（2.兰州理工大学能源与动力工程学院，兰州 730050）

0 引言

舰载直升机执行侦察、救援、反潜反舰等作战任务的能力出众，世界各国在发展驱逐舰、护卫舰等舰船的同时，也在全力研发适应各种任务的舰载直升机。由于无规则的海风、甲板尺寸的限制、船体的不规则运动、旋翼/舰船流场耦合等因素的影响，舰载直升机旋翼所处环境恶劣程度与流场复杂程度要明显大于路基环境。直升机旋翼桨叶一般形态细长，质地较为柔软，对外部气流变化敏感，在此环境下旋转时，旋翼桨尖易产生过度挥舞位移，进而与机身发生碰撞等安全事故，因此开展旋翼舰面气弹响应研究十分必要。

目前对舰船流场研究主要包括试验方法与CFD数值模拟的理论分析。在实船试验领域，W.D.Jr Reddy通过对比激光测速装置等装置在舰船流场速度测量上的结果，研究了舰船尾流测量与流场可视化的方案选择；B.T.Cheney等对SFS2等舰船缩比模型进行多次风洞试验，所获得的流场速度与压力结果为后续CFD研究提供宝贵的验证数据。CFD数值模拟方面，D.M.Roper等通过商用CFD软件对SFS2舰船尾流流场开展了相应的数值计算，得出了与实际较吻合的结果。在舰载旋翼动力学研究方面，S.J.Newman先是推导桨叶的挥舞运动方程，再运用模态叠加等方法开展研究，在考虑了重力和离心力的作用下，使用准定常空气动力学理论计算桨叶气动力载荷，结果表明在风速为50 kn（1 kn=0.514 444 m/s）、垂向速度为15 kn时，桨叶超过了挥舞极限，会与机身发生碰撞。

在国内，曲飞等首先通过CFD软件模拟了LHA-2舰船模型流场，并将所得定常数据与风洞试验结果及实船测量数据进行对比，得到了较好的拟合度，证实CFD技术的可行性；陆超等更进一步，对不同风向角时的LHA流场数值计算结果进行了分析比较，发现风向角的变化对舰船附近空气流场有显著影响。但是这些研究并未考虑直升机桨叶在流场中所受的影响。郑兆昌等进行了直升机旋翼/机体耦合系统的气弹响应分析，采用中等变形梁模型，同时引入桨叶绕挥舞铰等的刚性运动计算旋翼/机体的耦合响应；杨卫东等以中等变形梁为基础研究了带后掠桨尖旋翼的气弹响应和稳定性分析。但上述研究并未考虑旋翼在舰船环境流场下的响应。康浩等完成舰面旋翼瞬态响应分析方法的建立，研究了舰面旋翼启动、停车过程中的气弹响应，但没有计入舰船非均匀尾流的影响。

鉴于以往研究的不足，本文应用CFD方法获得不同条件下更详细的舰面流场信息，根据尾流场信息运用桨叶动力学模型求解旋翼舰面气弹响应，进而提出旋翼舰面气弹响应分析方法，并通过与相关算例进行对比验证其正确性；通过改变流场来流速度、旋翼悬停位置与来流风向角等，分析不同参数对舰船流场与旋翼舰面气弹响应的影响与产生的原因，得到一些有意义的结论。

1 旋翼气弹响应计算分析方法

1.1 动力学建模

为了提高计算模拟效率，本文采用中等变形梁假设，将桨叶等效为一维梁与二维截面模型的组合，由位移应变关系可得桨叶展向应变为

式中：ε ，γ，γ分别为轴向应变，摆振、挥舞方向剪应变；，，为对应方向弹性位移；，为截面坐标；为应力函数。

桨叶运动方程可由广义Hamilton原理得出：

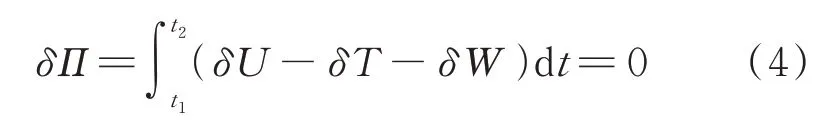
式中：，，分别为升机旋翼桨叶应变能、动能以及气动力等外力虚功的变分形式，具体表达式如式（5）所示。

式中：为拉伸弹性模量；为扭转弹性模量；为桨叶线密度；为重力加速度；δR ，F ，δφ，M 分别为广义位移，广义气动力，广义转角，广义力矩。

1.2 舰船流场CFD数值模拟与数据传输方法

由于本文研究的气体流动具有黏性，各区域间无能量交换，因此采用雷诺平均N-S方程作为控制方程。

连续方程：

动量方程：

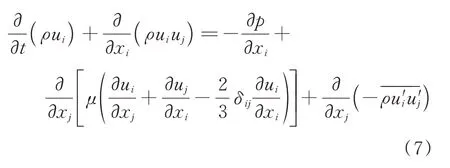
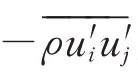
在考虑流体压缩性与流场模拟精度等因素后选择-两方程模型，该模型在反压力梯度下，边界层性能有所改进且此情况下无需计算壁面距离，可以更好模拟复杂的流动。

其湍流动能对应方程为

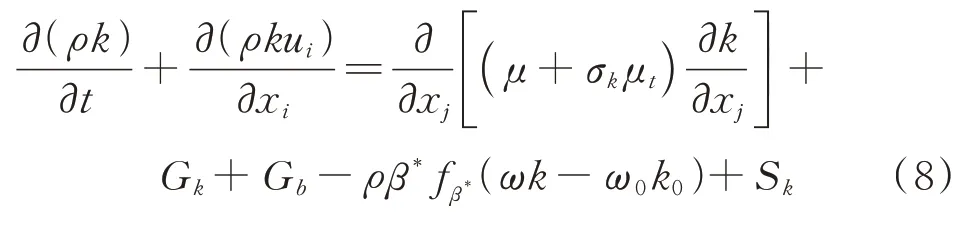
经模拟后的单位耗散率的传输方程为

式中：S 、S为指定源项；为湍动能；为单位耗散率；σ，σ分别为和的湍流普朗特数，σ=0.5，σ=0.5。

将式（8）和式（9）组合，即为标准-双方程湍流模型。

舰船模型选用国际通用的简化护卫舰模型SFS2。该模型结构外形简单，且有较为丰富的风洞试验数据用于对比验证，舰船建模如图1所示。

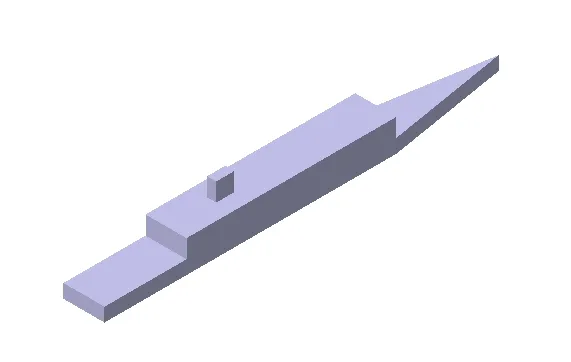
图1 SFS2舰船模型Fig.1 SFS2 ship model

本文采集CFD方法计算所得的流场信息，并通过旋翼附近探测点所获取的流场数据，组成流场速度数据库。然而在真实环境下舰面尾流场并不稳定，因此本文加入准定常湍流速度，尽可能模拟真实的舰船流场，则流场速度可表示为

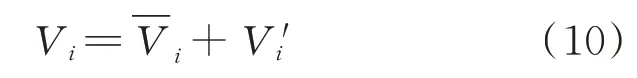
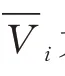
式中：σ为流场湍流系数；()为满足正态分布的随机数。

在计算旋翼气动力时，根据桨叶微段截面位置插入舰船流场速度信息，将CFD方法与桨叶动力学模型相结合，进而综合成本文使用的旋翼舰面气弹响应计算分析方法，让动力学模型求解结果计入舰船尾流场对直升机旋翼的影响，最终完成旋翼舰面气弹响应计算与分析。

2 旋翼气弹响应计算分析方法验证

2.1 模型气弹响应验证

为了验证模型气弹动力学分析的正确性与可靠性，选用文献［19］给出的前飞状态的旋翼为算例，旋翼具体参数如表1所示。

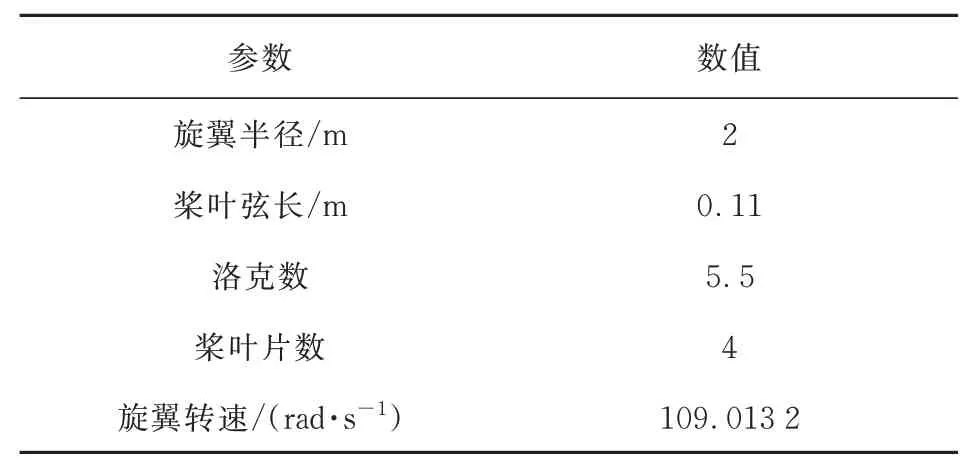
表1 算例旋翼参数Table 1 Example rotor parameters

计算可得算例旋翼在前进比为0.3时的桨尖气弹响应计算值，与文献［19］的对比结果如图2所示，其中桨尖响应位移为无量纲量。

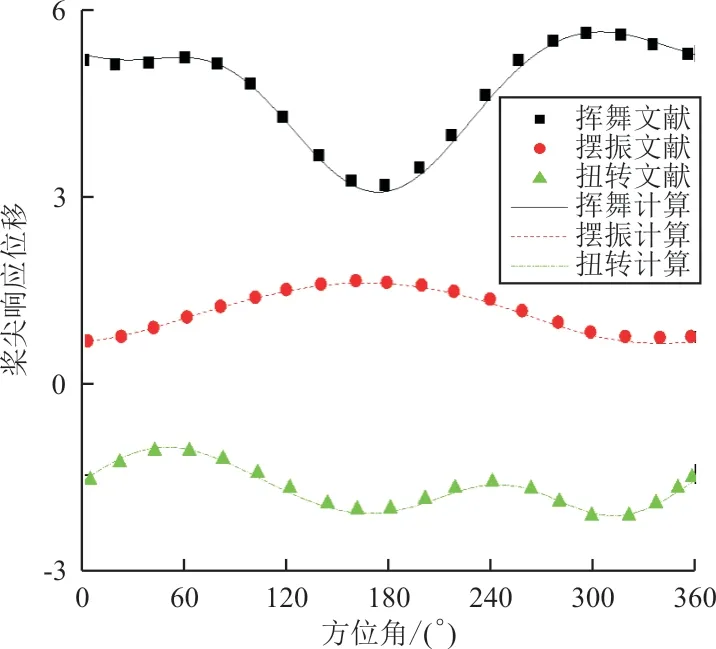
图2 旋翼桨尖响应曲线图Fig.2 Rotor tip response curve

从图2可以看出：桨尖响应在挥舞、摆振与扭转方向位移总体较小，其中挥舞位移占总位移比重最大，整体满足桨叶中等变形的条件。同时，计算所得的桨尖响应结果与文献值吻合较好，说明本文建立的桨叶动力学模型在计算旋翼气弹响应时的正确性与有效性。

2.2 CFD数值模拟方法验证

根据文献［3］的风洞试验，舰船来流速度为12 m/s，来流风向角为0°，设置计算域入口边界条件来流速度12 m/s，与舰船夹角为0°。在50%甲板位置，沿舰船甲板横向与机库等高，考虑此处流场的三方向速度分布，CFD计算结果与试验测量结果如图3所示，可以看出：CFD数值模拟计算结果与试验基本相同，虽有少许误差，数据大体上吻合较好，说明本文所使用数值模拟方法的正确性。

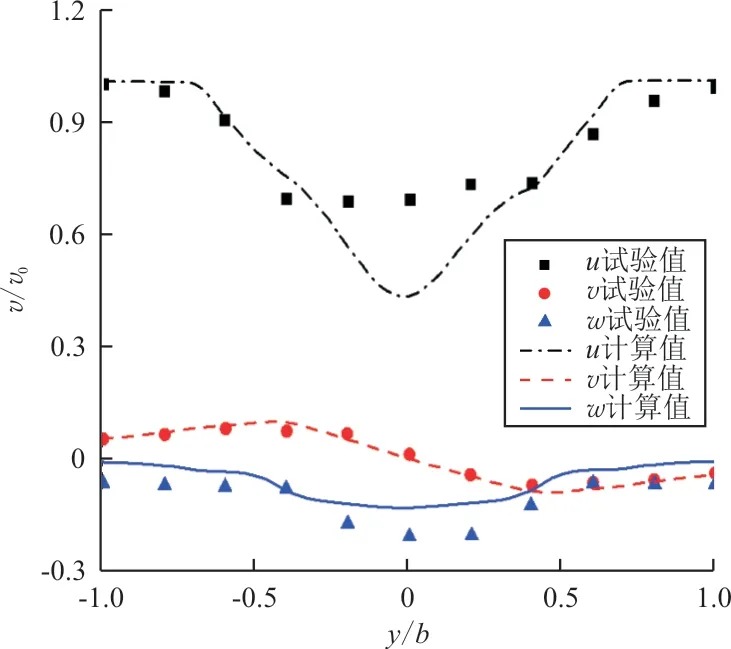
图3 速度分量计算值与试验值Fig.3 Calculated value and test value of velocity component

3 舰面气弹计算结果与分析

第2节完成了旋翼气弹响应计算与CFD数值模拟方法的建立，并通过与参考文献试验数据进行对比验证了研究方法的准确性。本节将运用这些方法，针对舰载直升机旋翼在舰面环境下进行流场分析与气弹响应研究，并分析来流速度、旋翼悬停位置和来流风向角等不同参数对旋翼气弹响应的影响。

3.1 旋翼舰面气弹模拟

选择“山猫”HMA.MK8直升机的简化旋翼为具体研究对象。“山猫”为英国海军型直升机，机身高度为3.67 m，无铰式旋翼且旋向为右旋，具体参数如表2所示。

表2“山猫”旋翼桨叶参数Table 2 Parameters of HMA.MK8 rotor blade

通过改变旋翼转速，计算桨叶在不同转速下的频率，可得桨叶共振图如图4所示，可以看出：在旋翼工作转速下，桨叶各低阶模态频率区别明显，此时桨叶各阶模态耦合情况较弱，不易发生共振现象，表明本文研究的旋翼对象结构设计较为合理，可以进行更为深入的气弹响应研究。

图4 桨叶共振示意图Fig.4 Schematic diagram of blade resonance

采用上述研究方法对舰船流场进行流场仿真并收集旋翼附近流场信息，调整舰船前方来流速度和旋翼位置等参数后再进行旋翼气弹模拟。

3.2 来流速度对旋翼气弹响应的影响

由于海上流动不规律的海风，舰船在现实中行驶会遇到不同海风天气的环境，而一般舰船航行速度为30 kn（约15.43 m/s），规定船尾至船首方向为0°风向角，选取来流速度20、30、40 m/s，风向角为0°，对不同来流速度下舰船流场进行数值计算，所得结果如图5所示，可以看出：在前方来流条件下，甲板区域分为靠近机库的前方低压区与甲板中后部靠近船尾的高压区；而由于靠近机库低压区的存在，流向甲板中后段的气流不会全部流出甲板区域，部分靠近低压区的气流会由于压力差改变流向，进而形成机库附近的气流回流区；甲板中后部的高压区域则是流过机库的气流改变流向后冲击到甲板壁面所致，随着来流速度的增加，甲板前后两区域的压力差逐渐增大。

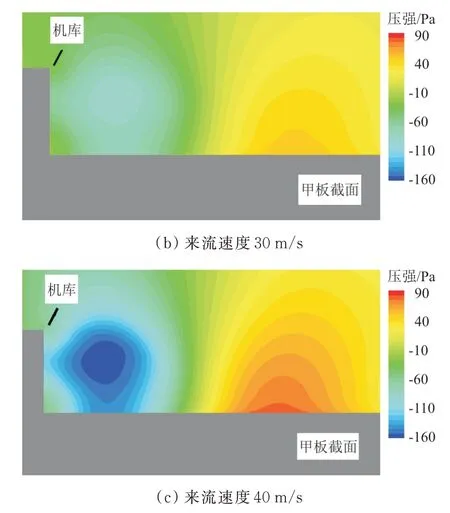
图5 不同来流速度下甲板区域压力云图Fig.5 Deck area pressure cloud at different inlet velocities

由于旋翼中心位于甲板纵向中轴线上，距离机库12 m且在甲板平面高度5 m，即0B、H5位置处，将旋翼附近的流场信息采集并计算不同来流速度下，旋翼桨叶的气弹响应，所得结果如图6所示，其中桨尖挥舞位移为无量纲量。从图6（a）可以看出：随着来流速度的增加，旋翼桨尖响应位移幅值逐渐增大，最大位移从8.50%（20 m/s）变化为9.21%（40 m/s），响应幅值增加了8.35%；桨尖位移变化沿方位角分布趋势一致，来流速度的改变对旋翼气弹响应的幅值影响更明显，远大于对幅值分布相位的影响。而在非定常流场下，桨叶在不同来流速度下的气弹响应响应最大值均有所增加，但波形趋势基本一致。因此可以得出，舰船流场来流速度对旋翼气弹响应影响较大，速度幅值越大，桨尖的挥舞位移最大值越大。

图6 不同来流速度下旋翼气弹响应Fig.6 Rotor aeroelastic response at different inlet velocities

3.3 悬停位置对旋翼气弹响应的影响

考虑到舰载直升机在着舰过程中，其旋翼所处位置并非一成不变，为了研究旋翼悬停位置对旋翼气弹的影响，选取旋翼四个不同位置状态（如图7所示），即位于距机库12 m，甲板中轴线高5 m（即图7中H5位置）、10 m（H10）两处以及距机库12 m，高5 m，左舷距甲板中轴6.858 m（即图中0.5B位置）与13.716 m（1B）两处。

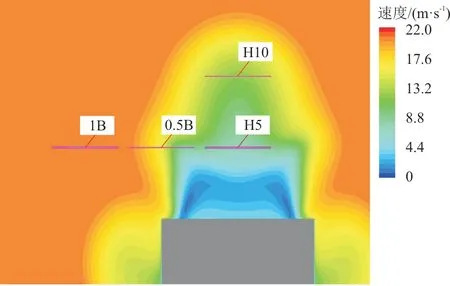
图7 旋翼中心截面速度云与位置示意图Fig.7 Rotor center section speed cloud and position diagram

图7中截面距机库12 m，为了清晰表示旋翼中心位置，图中旋翼尺寸并非真实计算尺寸。计算并分析在0°风向角，来流20 m/s条件下，旋翼在0B，5 m位置的气弹响应，计算结果如图6（b）所示。

不同悬停位置下旋翼瞬态气弹响应如图8所示，其中桨尖挥舞位移为无量纲量。

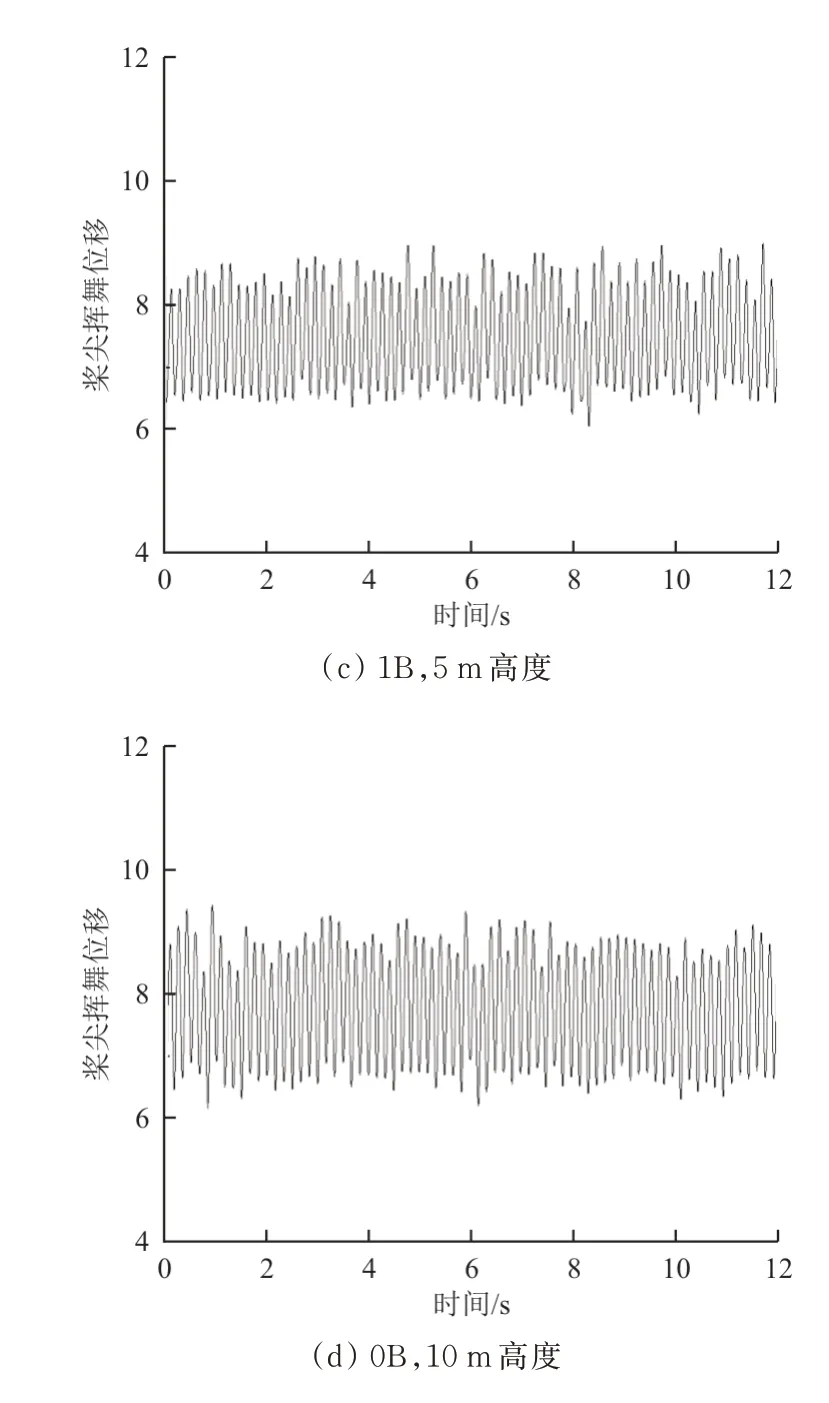
图8 不同悬停位置下旋翼瞬态气弹响应Fig.8 Rotor transient aeroelastic response at different hovering positions

从图8可以看出：当旋翼处于0B，5 m位置时，由于流场分布沿甲板中轴线对称，桨尖气弹响应沿180°方位角对称分布，且由于舰船尾流并不均匀，挥舞位移最大值与最小值过渡并不平缓；在0B，10 m位置处，前方来流没有机库等建筑的遮挡，速度幅值增大，但垂向速度分量有所减小，故气弹响应分布依旧沿180°方位角对称，挥舞位移最大值较0B，5 m位置几乎一致，最小值减小8.32%。同时由于该处流场分布较为均匀，位移最大值与最小值过渡更为平缓。

与0B，5 m位置相比，0.5B，5 m位置气弹响应位移最大值、最小值与其基本一致，只在响应方位角分布有明显区别，这是由于旋翼处于0.5B，5 m位置时，有一半旋翼在甲板外，因此该位置挥舞位移最大值出现在270°附近，并且位移响应分布更为集中；当旋翼位于1B，5 m位置时，由于此时旋翼已逐渐脱离舰船尾流场，左侧基本远离舰船流场，只在靠近甲板的旋翼右侧受舰船尾流影响，则此时旋翼气弹响应最大值与0B，5 m位置相比，减小4.5%，且出现在方位角230°附近。不难得知，旋翼悬停位置主要影响桨尖位移响应沿桨盘方位角的分布与最大值出现的桨盘方位角，对响应幅值影响不大。

3.4 风向角对旋翼气弹响应的影响

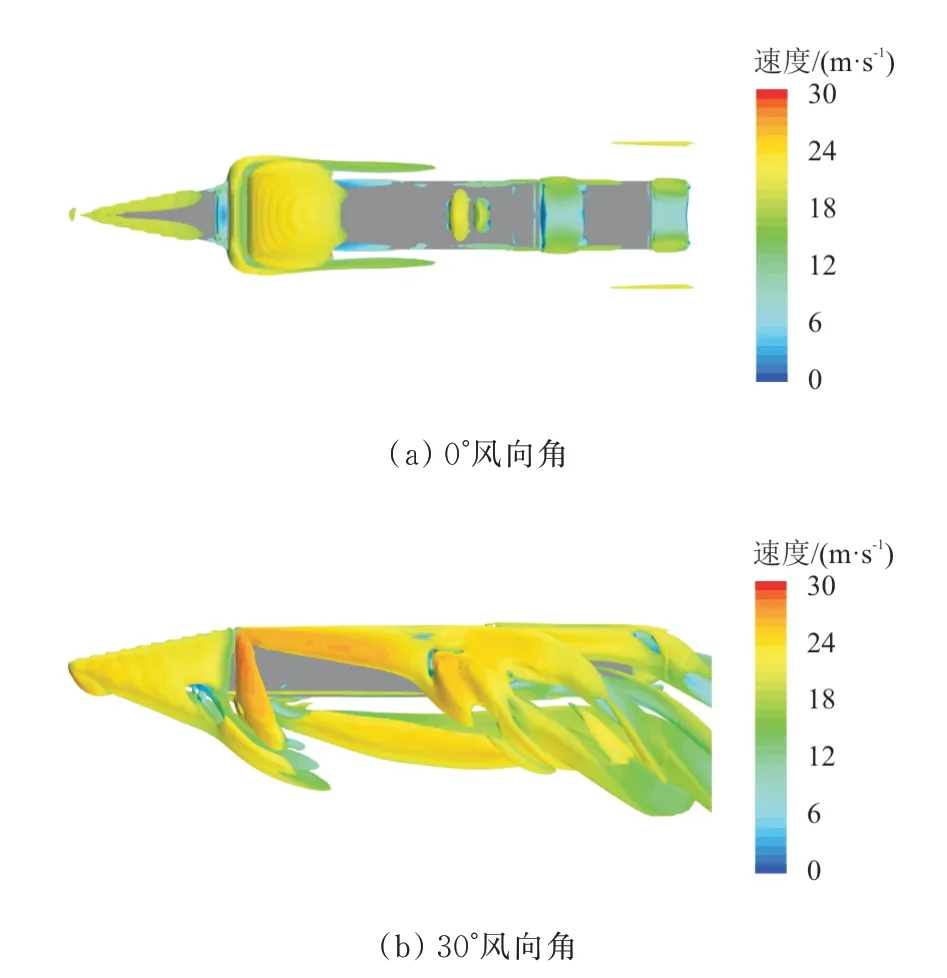
由于海上风向不固定，不同风向角下的甲板流场并不相同。选取舰船流场在0°风向角、右舷30°风向角、右舷60°风向角三种工况，来流速度20 m/s，旋翼在0B，5 m位置条件下，对舰船流场等值涡量进行仿真计算。

在=0.5的情况下，以速度幅值着色的舰船流场等值涡量图如图9所示。当来流为0°风向角时，流场中涡结构关于舰船首尾方向对称，并且主要集中与建筑形状改变较大，出现气流分离的位置，这与3.2节速度云图所得结论一致。而当来流角变为右舷30°时，流场漩涡结构向左倾斜，大量集中在船首与船尾部分位置。来流经过机库右侧后，向甲板区域发展出大量复杂的湍流涡，并向左后方继续发展逐渐远离甲板左侧。随着来流风向角继续增大，舰船上方区域逐渐被侧方来流在船体边缘气流分离产生的漩涡结构覆盖。此刻甲板区域受流经机库处的气流影响减小，虽然在侧方气流所形成的涡环境下，流场依旧较为复杂，但是在甲板右后区域漩涡结构数量有所降低，并且分布较风向角30°也更为均匀。

图9 不同风向角下舰船流场等值涡量图Fig.9 Equivalent vorticity diagram of ship flow field at different wind direction angles

为了对甲板区域流场进行更加细致的研究，本文于不同来流角度情况下，在50%甲板位置，机库高度处，检测流场垂向速度分布，所得结果如图10所示。

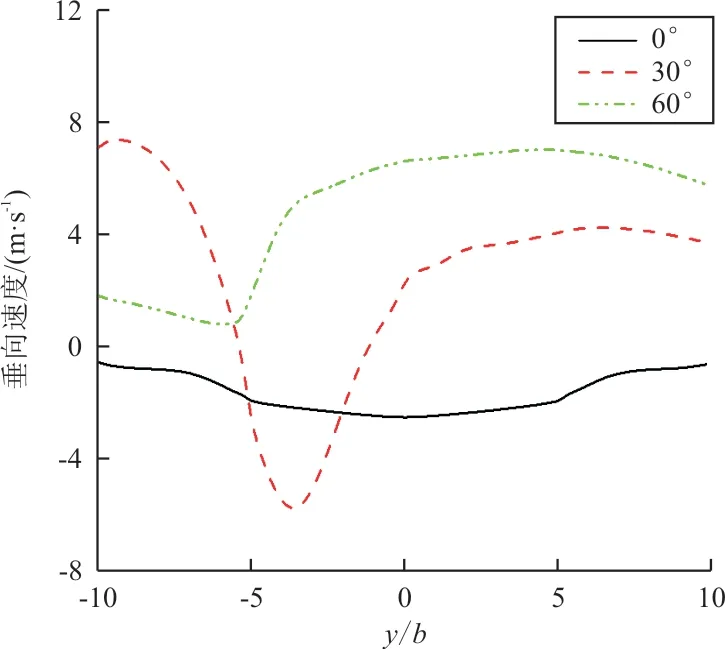
图10 不同风向角下垂向分速度分布曲线Fig.10 Vertical Velocity Distribution Curves at Different Wind Angles

从图10可以看出：随着来流角度的增大，甲板区域上方流场垂向速度分布不再对称，且与0°、60°来流角相比，30°来流角下垂向速度变化分布更陡峭，这与前面流场分析结果一致。

不同风向角下旋翼桨尖的挥舞位移响应曲线如图11所示，其中桨尖挥舞位移为无量纲量，可以看出：来流角度的增加对旋翼气弹响应变化有较大影响，与0°风向角8.50%最大桨尖位移相比，30°与60°风向角气弹响应位移最大值为11.44%、9.72%，分别增大了34.59%和14.35%，且最大值所在方位角变为140°附近。

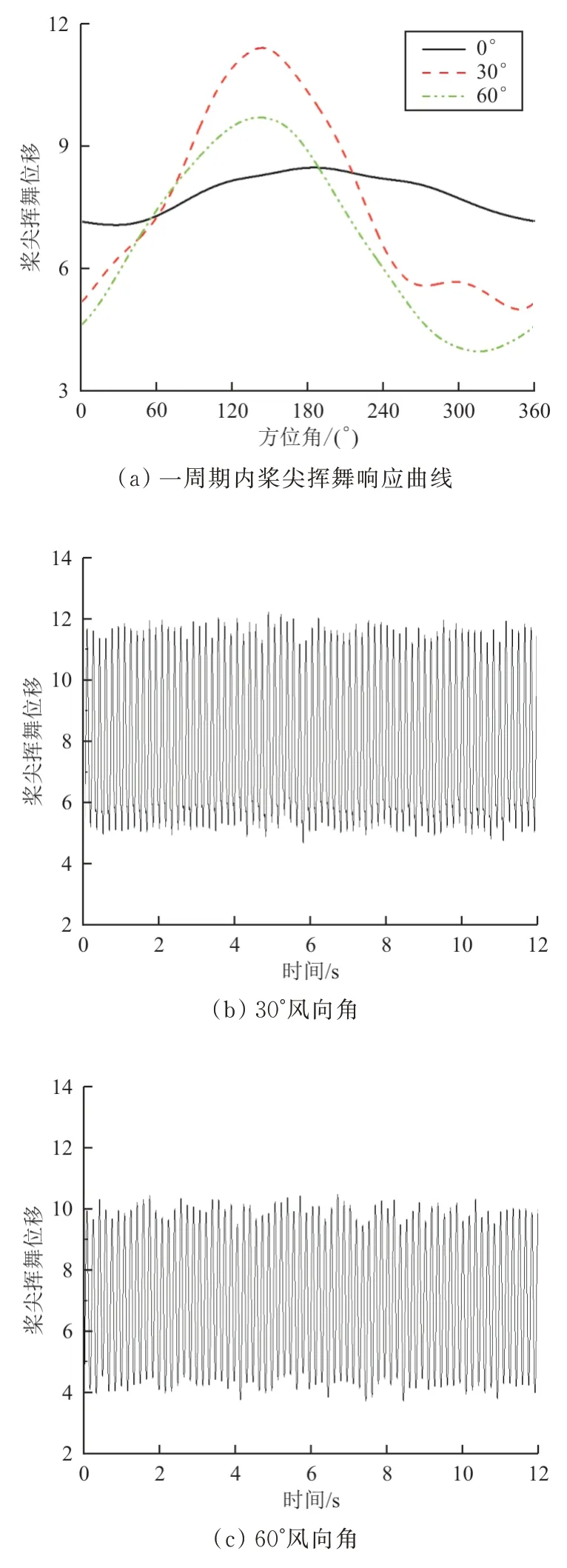
图11 不同风向角下旋翼气弹响应曲线Fig.11 Rotor aeroelastic response curves at different wind directions

30°风向角下计算所得气弹响应最大，峰值较60°风向角结果大17.70%左右，这是由于风向角30°时，旋翼所处位置垂向速度分布极不均匀，桨盘整体处于紊乱的舰船尾流中，导致旋翼气弹响应位移最大值变大。而当风向角为60°时，虽然垂向速度均值略有增大，但沿桨盘分布更均匀，故桨尖位移响应有所减小。不难得知，来流风向角对旋翼气弹响应的影响非线性变化，它与着舰域流场分布息息相关，因此需要将舰船尾流场与旋翼气弹响应分析相结合，才能为舰载直升机起降安全提供建议与保障。