大学物理实验成绩影响因素的形成性评价研究
2022-08-10钟志强张毅宁
钟志强,张毅宁
(鞍山师范学院 物理科学与技术学院,辽宁 鞍山 114007)
形成性评价是指在教学过程中为了解学生的学习情况,及时发现教和学中的问题而进行的评价.通过评估学生需求和监测学习进展,适当地设计学习顺序,调整教学策略,从而改良教学计划,以便有效地促进学习目标的完成[1].
追踪(纵向)数据是随着时间对每个个体进行重复测量得到的测量结果,其综合了截面数据和时间序列数据的所有特征[2],揭示了个体随时间的变化趋势、个体间差异和变量间因果关系.形成性评价的研究者利用追踪数据方法与工具,不仅可以关注某一特质随时间的发展趋势,而且可以进一步解释个体之间发展趋势的差异及其存在差异的原因,从而能够更加有效和精准地推动教学改革、提高教学质量.本文利用文献[3]得出的结论即以教师的教学投入和学生对教师反馈的利用是影响大学物理实验成绩的主要因素、教师投入具有跨层交互作用为立论基础,利用其中系列实验的考核与评价数据,借助Mplus 7.4统计分析软件,探索大学物理实验学习过程中的形成性评价的影响因素.
1 追踪模型的确立
追踪研究可分析个体心理与行为发展变化的一般趋势和个体间差异,探索变化规律和变量间的因果关系[4].前期研究方法主要有重复测量方差分析、多元回归分析、潜变量增长曲线模型(Latent Growth Curve Modeling,LGCM)及潜变量混合增长模型(Latent Growth Mixed Modeling,LGMM)[5].当前,潜类增长模型(Latent Categroical Growth Modeling,LCGM)与混合增长模型(Growth Mixture Modeling,GMM)成为常用处理群体异质增长的模型[6],这二者都是通过增长特征参数(截距和斜率)的均值来描述平均的增长趋势,通过增长特征参数(截距和斜率)的随机效应(方差)大小来描述个体之间增长趋势的差异,二者的区别主要在于类别组内的发展轨迹是否存在方差变异.
在实际应用中,由于个体之间发展趋势可能存在差异,而发展趋势上的差异可以通过潜在的变化类别,即分类潜变量来描述.混合增长模型可以帮助研究者探明潜在的不同变化类型,并检验不同类别中预测变量和结果变量之间的关系,这些成为实验模型确立的理论基础.参考相关研究[7-8],确定二者的基本公式为
yit=η0i+η1i×λt+εit,
η0i=α0+r0×wi+ζ0i,
η1i=α1+r1×wi+ζ1i,
其中,i=1,2,…,n,表示个体,n为样本量;t=1,2,…,T,表示测量时间点,T为测量总次数.yit表示个体i在时间点t时的得分;η0i为个体i轨迹的截距即初始水平;η1i为个体i成长轨迹的斜率;λt表示时间间隔值,如:0,1,2,3,…;εit为个体i在时间点t时的残差项;α0和α1分别表示全部个体截距和斜率的均值,由于假设每个个体具有相同的初始值,因此也称固定系数;wi为个体i的协变量,其与时间变化无关,但与yit有关;ζ0i和ζ1i分别表示个体截距和斜率与对应总均值间的差异,每个个体均有一个不同的值,所以也称作随机系数;r0和r1为协变量系数,也是斜率值.
2 基于追踪模型的形成性评价
2.1 潜类增长模型建立与分析
通过路径图可以更好地表达增长模型的特点,利用Mplus建模生成模型图.由于Mplus不能显示建模初始状态(如AMOS),只能将其运行结果(带拟合系数)一并展示,如图1所示.
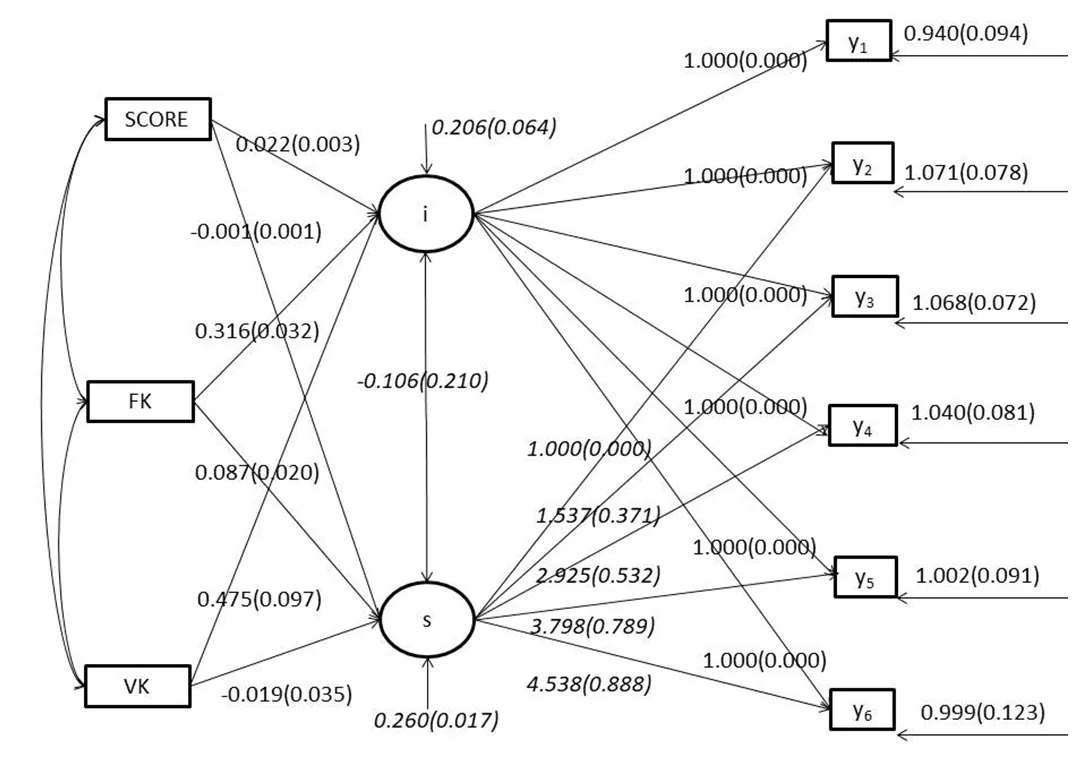
图1 带有协变量的学生成绩增长模型图
图1表示用6次重复测量的大学物理实验成绩作为观测指标(y1~y6)定义潜变量截距(intercept,i)和斜率(slope,s)两个因子.高考物理成绩(SCORE)、是否看微课(VK)、对教学反馈信息的利用程度(FK)3个变量,均值与方差有显著不同(见文献[3]中表1),因而可以将其作为协变量,用以分析是否对物理实验的初始成绩和发展变化有影响.
各截距(i)和斜率(s)的均值和方差参数表征组间和组内差异:对任何观测个体来说,截距是个常数,一般为1;斜率均值反映个体间增长,表示时间点间的平均增长率,斜率方差越大表明个体间发展轨迹差异越明显.本例中的时间测量点仅与测量的先后有关,与测量的间隔无关,因而采用自由估计.前2次载荷为固定值0和1,后4次为自由估计.不同的设定可以表示不同的时间函数或增长类型[9].两个潜在因子(i,s)可以共变,用双向箭头表示.
Mplus运行的模型拟合结果见表1.各项主要模型拟合指标均符合标准[10].近似误差均方根(RMSEA)受样本容量的影响较小,对错误模型比较敏感,是比较理想的指数;标准化残差均方根(SRMR)则是将此残差转换为Z分数.RMSEA与SRMR越小越好.比较拟合指数(CFI)是目前使用最广泛的指标之一,也是最稳健的指标之一,即使是对小样本模型拟合表现也很好,多用于嵌套模型比较;Tucker-Lewis指数(TLI)在最大似然估计时有较好稳定性.CFI与TLI越大越好.

表1 潜类增长模型图拟合指数
如图1,重复测量截距(i)的载荷固定为1,表示每次测量时的截距不变.斜率载荷表示时间效应,自由估计结果为:1,1.537,2.925,3.798,4.538,基本属于线性增长.这一点也能从文献[3]的图1中反映出来,6次实验成绩呈线性变化.截距和斜率的均值与方差见表2.
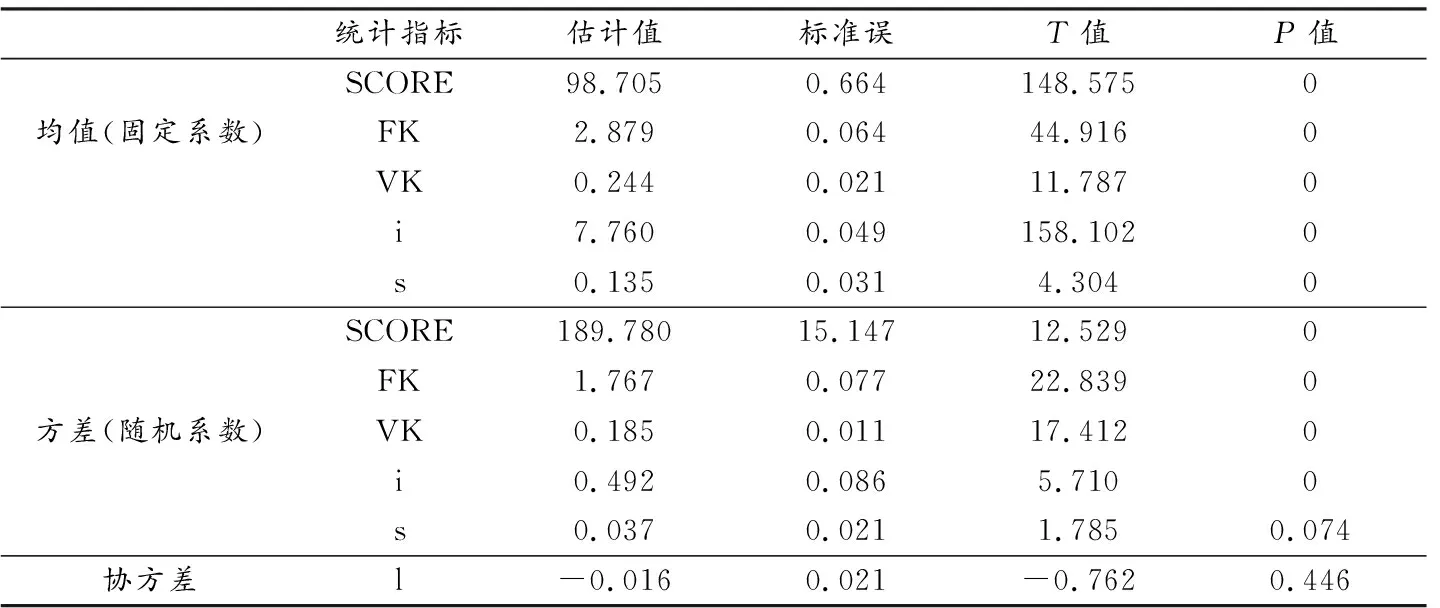
表2 截距、斜率等均值与方差表
表2中截距与斜率的均值均统计显著(P<0.05),说明测量的变化率和初始测量水平在测量个体间显著不同.具体包括:平均截距的估计值是7.760,说明第一次实验的平均分为7.760;平均斜率的估计值是0.135,说明平均斜率(6个时间点内)尽管增长不大,但却有增长趋势.截距与斜率的方差均统计显著(P<0.005),说明大学物理实验的个体间发展轨迹有区别.这一点也能从文献[3]的图1反映出,随机10人样本就有5个起点的变化趋势.截距和斜率之间的相关值(-0.016,P=0.446)表示平均截距与平均斜率的协方差统计不显著,说明实验分数的变化率与初始实验成绩无关.
高考物理成绩(SCORE)、是否看微课(VK)、对教学反馈信息的利用程度(FK)3个协变量,用以分析是否对物理实验的初始成绩和发展变化有影响.其对截距与斜率的影响见表3.

表3 学生高考物理成绩、微课、对教学反馈信息的利用程度对截距与斜率影响
从表3可知:学生高考物理成绩(SCORE)对物理实验初始成绩有微弱影响(0.022,P<0.05),对实验成绩增长没有直接统计意义(-0.001,P=0.231),可以认为高考物理成绩对实验成绩发展变化影响不大;微课(VK)对实验成绩有影响(0.475,P<0.05),对其成绩增长(-0.019,P=0.594)没有达到统计意义;教学反馈信息(FK)对学生的帮助程度、对实验初始成绩(0.316,P<0.05)及其增长(0.087,P<0.05)都有影响且影响显著.其直观表示见图1.
总之,通过数据分析得到如下结论:学生高考物理成绩对实验成绩的平均分有微弱影响;利用微课进行预习对实验成绩有影响;是否充分利用教学反馈信息对实验成绩影响相对较大.
2.2 混合增长模型分类的探索
尽管按学校类别分组已能够发现组间的差异,如文献[3]中图2所示,但是根据高考成绩进行学校类别分组却不能成为区分教学水平仅有的依据.高考成绩是入学的划分标准,如果仅以高考成绩判断教学效果,那么普通高校就会丧失教学改革的动力.对此,控制学校类别作为影响教学效果的因素,并对其做进一步探索.
从前面的分析得知:微课的预习和对教学反馈信息的利用能够实现学习成绩的提高,但二者变化程度有所不同.为进一步探索理论上教学成绩分类划分与归因,利用混合增长模型对学生成绩变化过程进行分类,探究是否有学习方式上差异,进而因材施教、调整教学.
实际上,潜类增长模型(LCGM)是混合增长模型(GMM)的特例,当潜类别变量只有一个类别时,GMM就成了LCGM[11].GMM模型的设定从基线模型开始,先设定单类别增长模型,然后逐渐增加类别个数.理想的研究情况是根据理论预测设定潜类别数目,但实际应用上多采用探索的思路,根据数据拟合结果选择模型.设定潜类别数目从1~7建立GMM模型,生成统计拟合系数,如表4所示.

表4 1~7种分类拟合系数汇总表
AIC、BIC和校正BIC(aBIC)是描述模型与数据拟合的指标,其值越小表示模型与数据的拟合越好;entropy值接近于1,表示有效清晰的分类;LMR与BLRT统计意义显著(P<0.05)[12].根据上述分类标准可知,6类是较好的分类,6个组别学习方式分组划分符合数据推演的理论结果.然而,在实际运用中,教师无法准备6套教学预案来实施教学改革,需要从其他角度对学习的状况再加以分类探索.
2.3 增长模型分组的再次确定
从文献[3]可知,教师投入具有跨层交互作用,学生对教学反馈的利用对各层级教学成绩都有较大的影响.从本文2.1潜类增长模型建立与分析中可知,是否充分利用反馈信息对实验成绩及其增长影响最大.由此,对数据再次处理,将反馈(FK)值大于3的值重置为1,小于等于3的值重置为0,以此作为分类标准建模,其执行结果见表5与图2.
从表5看出,模型拟合指数基本符合理论要求,少部分指标在参考边缘.从图2看出,在估计均值与样本均值中,不利用反馈组的两个曲线基本一致,利用反馈组的两个曲线也基本重合,两组曲线分布有明显组间差异,利用反馈组的平均成绩、初始成绩(截距)和成绩的增长(斜率)均高于不利用反馈组.

表5 利用反馈进行分组的增长模型拟合指数
在文献[3]的图2中,师范院校组成绩提高较快的原因在于师范院校的教师较多实践了教学反馈的环节.后经不完全调查,在3个师范院校实验报告的评阅中,除给出实验分数外,还针对分数较低的学生提出了不少改进意见,如明晰实验步骤、规范实验报告内容、深入实验原理思考、完善实验数据和具体指出实验错误等,从而提升了学生发现不足的积极性,及时改进了实验报告,落实了实验课程的形成性评价.

图2 利用反馈进行分组划分的增长模型图
此外,还利用了是否使用微课和高考物理成绩进行多次划分尝试,均未达到理想的模型拟合.
综合以上分析,得到如下结论:对教学反馈信息的有效利用是提高学生成绩、完善形成性评价的关键之处.从学生角度出发,学生接受反馈意见的程度是提高学生成绩的主要原因,只评价不反馈或者反馈却不能及时纠正学生错误与不足的教学行为对应着学习成绩的停滞不前;从教师的角度出发,应该做的是指出实验报告中的不足,提出报告改进意见,督促学生及时纠正.如此,形成性评价才能起到应有的作用.
3 研究结果与探讨
在文献[3]多层线性模型里的教师层面中,教师的教学投入(备课、实验器材准备和批改实验报告的时间)是决定学生成绩高低的关键因素,其他教师因素影响不具有统计学意义;在学生层面中,事先的预习和对教学反馈信息的利用对学习成绩的提高有正向影响.总之,教师的课前投入可以减少学生预习时间,从而提高学生学习效率和效果.
学生对反馈信息的利用掌握程度分散度较大,说明教师的反馈信息还不能成为全部学生提高学习效果的可利用因素,尚有很大改进空间.形成性评价研究表明,教学成绩的提高需要教师加大投入,主要是提高学生对批改信息的利用程度,应该让批改内容成为提高教学质量的可行措施.此外,教学的反馈信息也不是特指教师批改,优秀学生榜样的作用、学生之间的交流、正确信息的自主探究与获取等都是反馈信息获得的方式.这些引导学生利用反馈信息促进学习进步的方法,有待进一步尝试和实证.
教学反馈信息帮助学生理解学习目标,找出他们的实际学习水平与教学要求之间的差距,进而快速有效地提高教学效果.教师的教学反馈信息是否发挥作用关乎形成性评价的成败,形成性评价作用是否有效关乎学生成绩的提高.形成性评价不是一个个实验或作业的分数罗列,而是对学生错误问题的有效指导.
