季节变化下害虫综合治理切换模型的动力学性质研究

孙佳杰，刘 兵

(1.辽宁师范大学 数学学院,辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

庄稼地里过多的害虫会导致农作物品质下降、产量减少，使农业生产受到严重影响[1].为了减少害虫对作物的损害,最常见的是引进天敌和喷洒杀虫剂相结合的综合害虫控制方法[2-3].

目前,很多学者利用数学模型模拟综合害虫治理过程，如固定时刻脉冲的害虫综合治理模型、状态依赖脉冲的害虫综合治理模型、Filippov切换的害虫综合治理模型等[4-6].上述模型忽略了季节性变换过程中害虫休眠期与复苏期的种群变化率不同的问题[7].因此,利用脉冲切换模型模拟季节性变换下的害虫综合治理现象更加合理.本文考虑天敌在害虫休眠期以杂食为生、在害虫复苏期以害虫为食的天性,采用等周期喷洒农药和释放天敌的方式治理害虫,建立并研究季节变化下害虫综合治理的动力学模型,给出影响害虫灭绝与持续生存的关键参数.

1 模型建立

在季节变换下,把害虫种群的年度周期分成两个阶段：第一阶段为害虫休眠期.害虫种群由于外界因素影响线性率减少,此时天敌以杂食为生,假设其增长率为常数.第二阶段为害虫复苏期.假设害虫种群满足Logistic增长方式,天敌以害虫为食，在此期间,进行等周期喷洒杀虫剂和释放天敌,得到季节变化下的害虫综合治理动力学模型：

(1)

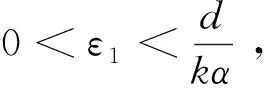
其中,x(t),y(t)分别表示t时刻害虫、天敌的种群密度;λ>0为t∈[nT,(n+l)T)时间段内,害虫种群休眠时的减少率;A>0为天敌种群在害虫种群休眠期[nT,(n+l)T)内以杂食为生的常数增长率;r>0,K>0分别为t∈[(n+l)T,(n+1)T)阶段害虫种群的内禀增长率和环境容纳量;α>0为t∈[(n+l)T,(n+1)T) 阶段天敌种群对害虫种群的捕食率;k>0为t∈[(n+l)T,(n+1)T)阶段天敌自身转化率;d>0为天敌种群的死亡率;T为年度周期;00为在t=(n+l)T+kTp,k=1,2,…,p时刻天敌的释放量.本文假设杀虫剂的喷洒和释放天敌周期为Tp,从而有(1-l)T=pTp.

2 害虫灭绝的阈值

首先,考虑当系统(1)害虫灭绝时，它的子系统的动力学性质：

(2)

定理1子系统(2)存在正周期解y*(t),并且对系统(2)的任何解y(t)都有：当t→∞时,y(t)→y*(t),其中,

(3)

证明系统(2)在脉冲区间nT≤t<(n+l)T的解为

在t=(n+l)T时刻害虫复苏,则有

当t∈((n+l)T,(n+l)T+Tp)时，

y(t)=y((n+l)T)e-d(t-(n+l)T),

在t=(n+l)T+Tp时喷洒杀虫剂和释放天敌,则有

y(((n+l)T+Tp)+)=(1-p2)y((n+l)T)e-dTp+μ,

当t∈((n+l)T+Tp,(n+l)T+2Tp)时，

y(t)=((1-p2)y((n+l)T)e-dTp+μ)e-d(t-((n+l)T+Tp)),

在t=(n+l)T+2Tp时刻喷洒杀虫剂和释放天敌,则有

y(((n+l)T+2Tp)+)=(1-p2)2y((n+l)T)e-2dTp+μ(1-p2)e-dTp+μ,

由数学归纳法可得,当t∈((n+l)T+(p-1)Tp,(n+1)T)时,

在t=(n+1)T喷洒杀虫剂和释放天敌,则

y(((n+1)T)+)=(1-p2)py((n+l)T)e-dTp+C,

把y((n+l)T)的值代入得

令

yn=y((nT)+),

则可得如下差分方程

(4)

由此差分方程存在唯一不动点

由于

且差分方程(4)是线性方程,因此y*是方程(4)的全局渐近稳定的正平衡点,从而系统(2)存在一个全局渐近稳定的正周期解y*(t),当t→∞时,系统(2)的任意解y(t)→y*(t),其表达式如(3)所示.证毕.

因此,由定理1知系统(1)存在害虫灭绝周期解(0,y*(t)),令

定理2如果R0<1,则系统(1)的害虫灭绝周期解(0,y*(t))是全局渐近稳定的.

证明设(x(t),y(t))是系统(1)以(x(0),y(0))为初始值的解,系统(1)的周期解(0,y*(t))的局部渐近稳定性可以利用系统的变分方程来确定,因此,作变换

x(t)=α(t),

y(t)=y*(t)+β(t),

则相应的线性方程的解为

其中,

是系统(1)的基础解矩阵,ψi(t)满足

其中,

ψ1(0)=ψi(0)=I

是单位矩阵,因此

在计算单值矩阵特征值的过程中,无须给出(*)的具体表达式.由Floquet理论知,如果单值矩阵

的两个特征值的模小于1,则害虫灭绝周期解(0,y*(t))是局部渐近稳定的.由M的表达式可以计算出其特征值分别为

从这则传说来看，腊八食粥习俗不一定始于宋时，恐怕要推至更远的年代。当然，在没有任何文字记载情况下，仅凭一则神话传说是不能断定某种习俗起源的。但是，这些目前还流传在豫东群众中的口碑资料，却为民俗学者，特别是饮食文化研究者提供了值得注意的线索。

λ2=(1-p2)pexp(-dT),

显然|λ2|<1,那么模型(1)的周期解是局部渐近稳定的充要条件是|λ1|<1,即R0<1.

下面证明系统(1)周期解的全局吸引性.因为R0<1,所以存在充分小的ε(ε>0),使得

成立.

由系统(1)的第2和第4个方程可得,

考虑如下脉冲微分方程

(5)

利用脉冲比较定理可知y(t)≥N(t), 当t→∞时，N(t)→y*(t).

y(t)≥N(t)>y*(t)-ε

(6)

成立.

假设(6)对∀t≥0成立,则有

由脉冲微分方程比较定理,当t∈[nT,(n+1)T)时,

x((n+l)T)=x((nT)+)exp(-λlT),

⋮

由于δ<1, 所以

x(nT)≤x(0+)δn,

且当n→∞,x(nT)→0,因此,当t→∞时,x(t)→0.

下面证明：当t→∞时,y(t)→y*(t).

由上面两个不等式的左端,可得

y(t)≥N(t),

并且

N(t)→y*(t),t→∞.

对于上面两个不等式的右端,考虑下面的微分方程：

当t→∞时,z(t)→z*(t), 其中,

因此,∀ε2>0,∃t2>0, 使得当t>t2时,有

y*(t)-ε2

令ε1→0,对t充分大时,有

y*(t)-ε2

从而,当t→∞时,y(t)→y*(t).

所以,当R0<1时,系统(1)的害虫灭绝周期解(0,y*(t))是全局渐近稳定的.证毕.

由定理2可知，当R0<1时，害虫种群必将灭绝.实际上，可以证明当R0>1时，害虫种群将会持续生存，因此，R0是害虫种群灭绝的阈值.

3 结论

本文建立了一个季节变换下害虫综合治理动力学模型,给出害虫灭绝的阈值R0.图1(a)和图1(b)分别给出了R0关于T与l的等高线、μ与p1的等高线,参数取值分别为：x0=0.5,y0=0.5,λ=0.2,A=1,d=0.3,r=0.5,K=1,α=0.5,p1=0.5,k=0.6,T=1,μ=0.4,p2=0.1.由图1(a)可知,害虫休眠时间l越长或者年度周期T越短,R0就越小,越有利于害虫治理.由图1(b)可知,随着杀虫剂p1对害虫瞬间杀死率的增加或者天敌释放量μ的增多,R0随之减小,这表明对害虫致死率较高的杀虫剂或者增加天敌释放量有利于控制害虫.

当T=1,l=0.25时,R0<1(见图1(a)),由定理2知,害虫灭绝周期解是全局渐近稳定的,而天敌是周期性震荡的.图2给出相应的时间序列图(参数取值同图1)，验证了理论结果的正确性.

图1 害虫灭绝的阈值等高线图

图2 害虫种群和天敌种群时间序列图