斜冲击下内凹六边形蜂窝结构的面内动态力学响应

刘 勇，苏步云，刘浩伟，树学峰

（太原理工大学机械与运载工程学院应用力学研究所, 山西 太原 030024）

负泊松比蜂窝结构作为一种可设计的人造结构[1]，具有正泊松比材料所不具备的力学性能，如抗剪切、抗断裂、吸能隔振等，因此引起了国内外学者的极大关注[2-3]，广泛应用于航空航天、医疗设备、缓冲保护装备等领域[4]。

已有研究表明，蜂窝结构的力学性能主要受几何拓扑结构与胞孔尺寸等因素的影响[5]。Ruan 等[6]分析了相对密度和冲击速度对正六边形蜂窝结构的变形模式和平台应力的影响，结果表明：随着胞元壁厚和冲击速度的改变，正六边形蜂窝结构会呈现出X、V 和I 形变形带。Li 等[7]对正六边形蜂窝结构在不同冲击方向下的临界损伤应力和能量吸收进行了研究。Hou 等[8]利用有限元模拟研究了不同胞壁厚度的内凹六边形蜂窝结构在不同冲击荷载下的变形模式和应力-应变曲线，并与正六边形蜂窝结构进行了对比分析。Hu 等[9]开展了内凹六边形蜂窝结构在不同内凹角度和不同冲击速度下的变形模式和泊松比效应的研究，指出蜂窝结构的承载能力与内凹角度和冲击速度相关，且负泊松比效应随着内凹角度的增大而增大。Liu 等[10]针对内凹六边形蜂窝和正六边形蜂窝结构在不同加载速度和不同相对密度下的变形模式和能量吸收进行了研究，结果表明，当应变相同时，内凹六边形蜂窝结构可产生更高的峰值应力以增强能量吸收。Li 等[11]对比了3 种蜂窝结构（正六边形、内凹六边形、混合结构）在不同冲击荷载下的变形模式和平台应力，结果表明：与单轴冲击相比，3 种结构在双轴冲击下的能量吸收能力和承载能力均增强；正六边形结构蜂窝在冲击荷载下的能量吸收与其他两种结构相比表现出明显的优异性。袁敏等[12]研究了具有梯度厚度的内凹六边形蜂窝结构的面内冲击力学特性，结果显示正向厚度梯度材料具有优良的吸能效果和抗冲击特性。

值得注意的是，实际应用中，蜂窝结构受到非理想加载的概率远大于理想加载。因此，对于材料在非理想条件下的动态力学性能研究十分必要。卫禹辰等[13]研究了内凹厚度梯度蜂窝在爆炸冲击荷载下的结构响应，得到了吸收冲击波的最佳尺寸梯度和角度梯度。Remennikov 等[14]采用实验和数值模拟方法研究了内凹六边形蜂窝结构在局部冲击荷载下的变形历程，结果表明，在局部荷载作用下，负泊松比蜂窝结构不仅表现出局部收缩特性，且在未承受荷载的区域呈现出膨胀现象。Wang 等[15]开展了三维正六边形蜂窝结构在不同倾斜荷载冲击下的动态力学响应研究，发现了I 形变形带伴随X 形变形带的新变形模式。马芳武等[16]研究了内凹三角形蜂窝结构在不同倾斜荷载冲击下的面内力学特性，并根据平台应力和能量吸收确定了最佳冲击倾角。Dhari 等[17-18]采用塑性铰追踪法提取了内凹六边形蜂窝结构在静态倾斜荷载下的微观变形机制，结果表明，在倾斜加载下，由于局部变形导致弹性段与平台段之间产生过渡阶段，导致能量吸收率峰值延迟。

综上所述，目前蜂窝结构的研究主要以理想加载为主，关于非理想加载的研究较少。然而，作为缓冲吸能材料，蜂窝结构在实际服役环境中普遍遭受斜向偏载，易诱发结构失稳，减损吸能能力，针对蜂窝结构在斜冲击下的动态响应研究是实际应用中的必要环节。因此，本研究通过建立内凹六边形蜂窝模型，采用ABAQUS 有限元软件研究其在不同斜冲击荷载下的面内动态力学响应。

1 计算模型

1.1 有限元模型

1.2 模型验证

为验证本研究所采用的有限元算法的有效性，按照文献[6]中的加载工况，进行了正六边形蜂窝结构的面内动态力学性能模拟，即约束试样左侧全部自由度，其他边缘未约束，冲击板以恒定速度碰撞试样。如图2 所示（ε 为应变），模拟结果与文献[6]中的研究成果基本一致，能够较好地再现正六边形蜂窝结构在动态冲击过程中双X 形变形带的形成，从而验证了本研究中建模及算法的可靠性。

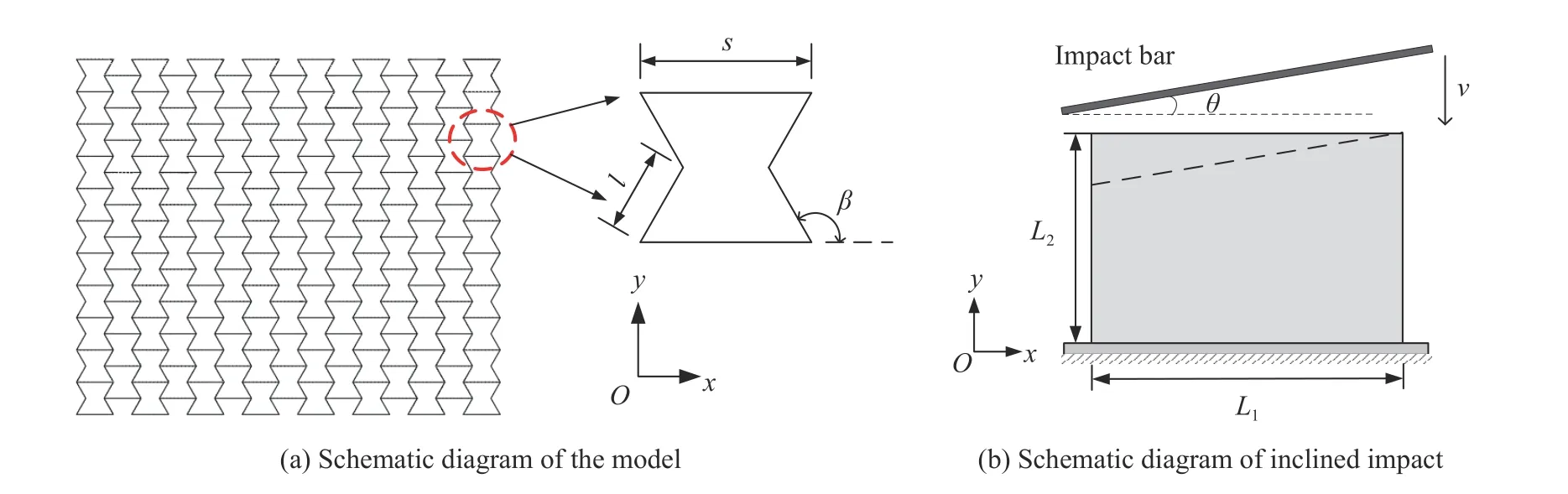
图1 内凹六边形蜂窝结构的斜冲击示意图Fig. 1 Schematic illustration of inclined impact of auxetic materials

图2 正六边形蜂窝结构沿 x方向面内冲击变形模式Fig. 2 In-plane impact deformation mode of regular hexagonal honeycomb materials along the x direction

2 计算结果与分析

本节从不同冲击速度和不同冲击倾角下内凹六边形蜂窝结构的变形机制、初始峰值应力和平台应力方面对其面内动态力学性能开展系统分析。

2.1 变形模式分析

由于斜冲击中无法按照应变定义进行量化分析，为了有效地对比材料在不同斜冲击程度下的变形模态，提出了无量纲时间参数t

式中：t为冲击时间。

图3 给出了不同斜冲击条件下内凹六边形蜂窝结构的面内变形过程。从图3(a)可以看出，低速冲击（v=6 m/s）、 θ=0°时，内凹六边形蜂窝结构发生整体变形，呈现出X 形变形带。随着冲击倾角的增大（ θ=2°），材料逐渐向右倾斜，形成X 形变形带；而当 θ≥4°时，材料在冲击端发生局部变形，随后逐层变形至材料底部。当冲击速度提升至30 m/s、 θ=0°时，如图3(b)所示，变形初期材料在冲击端产生局部I 形变形带，随后呈现出X 形变形带。与正冲击（ θ=0°）不同的是， θ>0°时，冲击端的I 形变形带产生的分层逐渐消失。出现这种现象的原因是斜冲击下材料左端先发生变形，形成变形带，导致两侧变形时间不同，形成分层。随着冲击速度不断提升至100 m/s、 θ=0°时，如图3(c)所示，材料逐层坍塌，形成I 形局部变形带，最终完全密实化。当冲击倾角发生变化（ θ>0°）时，仍呈现I 形变形带。

图3 内凹六边形蜂窝结构在不同倾斜角度和冲击速度下的变形过程Fig. 3 Deformation of auxetic materials under different inclination angles and impact speeds

对于上述3 种变形模式，可以使用图4 所示的分类图来总结。其中，局部变形是指内凹六边形蜂窝结构在斜冲击中部分发生变形，且局部变形部位没有明显的变形带堆积现象，无明显的负泊松比特征，主要发生在低速冲击且冲击倾角较大的工况；I 形变形带是指胞元从冲击端逐层坍塌，主要发生在高速冲击中；X 形变形带是指胞元在冲击中向内收缩形成变形带，且呈现出明显的负泊松比特征。从图4 中可以看出，当冲击速度较低时，冲击倾角的存在导致材料的变形模式从X 形变形带转为局部变形。然而在高速冲击时，冲击倾角对材料变形模式的影响逐渐减弱，均为I 形变形带。

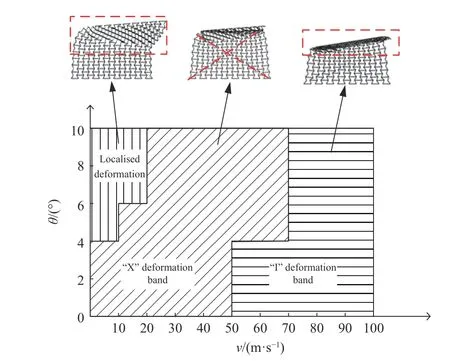
图4 变形模式分类Fig. 4 Classification of deformation modes

为分析负泊松比效应对蜂窝结构变形模式的影响，图5 对比分析了正六边形蜂窝结构与内凹六边形蜂窝结构在相同冲击工况下的变形模式。可以看出，在低速冲击（冲击速度为3 和10 m/s）时，正六边形蜂窝结构为整体变形，而内凹六边形蜂窝结构为局部变形。当冲击速度为30 m/s 时，正六边形蜂窝结构产生I 形变形带，而内凹六边形蜂窝结构处于过渡模态，X 形变形带伴随着局部变形产生。当冲击速度为50 m/s 时，二者均产生I 形变形带，但由于泊松比存在正负差异，正六边形蜂窝结构表现为向外膨胀，而内凹六边形蜂窝结构则表现为向内收缩。通过对比两种蜂窝结构的斜冲击变形模式可以发现，在相同工况下，内凹六边形蜂窝结构发生变形晚于正六边形蜂窝结构。观察可知，在斜向荷载作用下，内凹六边形蜂窝结构胞元仍向内收缩，产生负泊松比效应，但由于结构的不稳定性导致其倾倒，延缓了其变形模式的产生。因此，内凹六边形蜂窝结构由于受到负泊松比效应的影响，变形模式产生延迟。

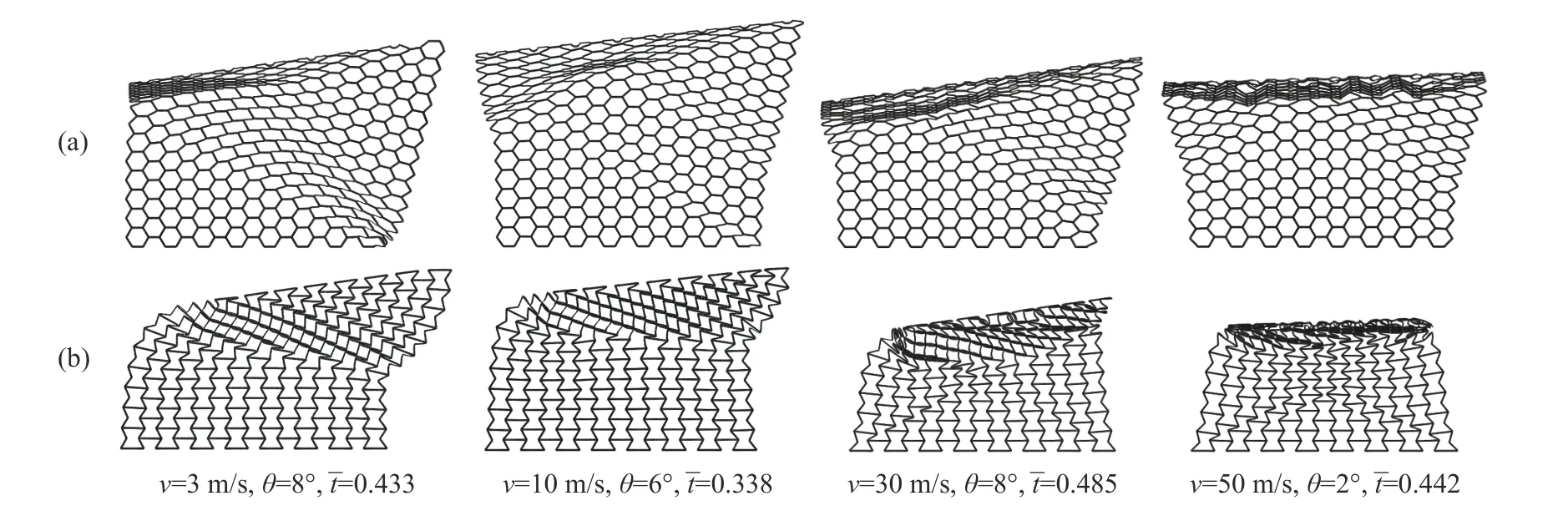
图5 正六边形蜂窝结构 (a) 与内凹六边形蜂窝结构 (b) 的变形对比Fig. 5 Comparison of deformation mode of regular hexagonal honeycomb (a) and auxetic materials (b)

2.2 应力时程分析

通常采用工程应力、工程应变的方法（方法1）来表征正冲击下的蜂窝结构，即

采用上述两种方法获得的应力-时程曲线如图6 所示。可以看出，两种方法的主要差别在于对变形初期的应力表征。由于在斜冲击变形初期，材料与冲击板的接触面积较小（见图3），接触力较小，因此采用方法1 得到的应力也相对较小。而采用方法2 得到的应力能够较好地描述材料局部应力的激增，更好地反映冲击应力从局部到整体的变化。此外，在变形中后期，接触面积保持恒定，尽管方法2 与方法1 相比横截面积较大，但由于引入了横向力Fx，两种方法得到的应力几乎没有差别。因此，当需要考虑材料的局部行为时，本研究提出的方法2 的处理方式更合理。

图6 两种方法得到的应力-时程曲线对比Fig. 6 Comparison of stress-time curves obtained by two method

如图7 所示，采用方法2 得到的斜冲击下蜂窝结构的应力-时程曲线与其在正冲击下的应力-时程曲线相似，具有3 个变形阶段，即弹性段、平台段和密实段。从图7 中可以看出，内凹六边形蜂窝结构在不同冲击倾角下具有不同的初始峰值应力，随着倾斜角的增大，平台段和密实段应力呈下降趋势。图8给出了不同冲击速度下的应力-时程曲线。结果表明，当倾斜角相同时，内凹六边形蜂窝结构的初始峰值应力随冲击速度的提升逐渐增大。通过图7、图8 的对比可知，不同冲击速度和冲击倾角下材料平台阶段的动力响应差别较大，因此需要对平台应力开展进一步分析。

图7 不同冲击倾角下的应力-时程曲线Fig. 7 Stress-time curves under different impact angles

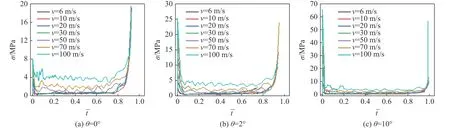
图8 不同冲击速度下的应力-时程曲线Fig. 8 Stress-time curves under different impact velocities

2.3 平台应力

图10 给出了不同倾斜荷载作用时的能量吸收曲线。从图10(a)中可以看出：当倾斜角θ=2°时，材料在达到密实段附近时的能量吸收（E）与θ=0°时相差不大；除此之外，材料的能量吸收随倾斜角增大逐渐降低。从图10(b)、图10(c)可以看出，当冲击速度达到30 m/s 时，在倾斜荷载的倾斜角较小时，材料的能量吸收差别不大，随着倾斜角的增加，吸能能力逐渐减弱；当冲击速度达到100 m/s 时，可以明显地看出材料的能量吸收随冲击倾角增大逐渐减小。图11 给出了同一倾斜角、不同冲击速度下的对比，可以看出：在低速冲击时蜂窝结构的能量吸收差别不大；但随着冲击速度的提升，蜂窝结构的能量吸收显著增加。这与图9(a)中得到的结论一致。此外还可得知，由于结构的不稳定性，在斜冲击下内凹六边形蜂窝结构发生倾倒将导致吸能能力减弱。

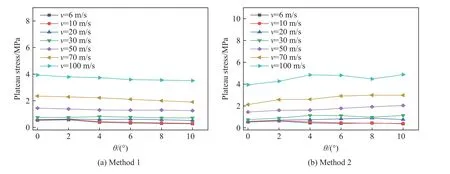
图9 两种方法表征的平台应力变化曲线Fig. 9 Plateau stress curves obtained by different methods

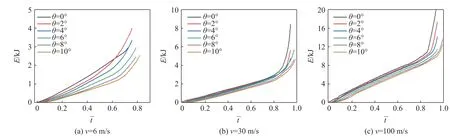
图10 冲击倾角对内凹六边形蜂窝结构能量吸收的影响Fig. 10 Influence of impact angle on energy absorption of auxetic materials

图11 冲击速度对内凹六边形蜂窝结构能量吸收的影响Fig. 11 Influence of impact velocity on energy absorption of auxetic materials

通过图10 与图11 的分析可知，与方法2 对比，方法1 得到的平台应力更符合材料在斜冲击下的能量吸收。从图3 中的变形后期可以看出，当存在冲击倾角时，材料达到密实段时，仍有部分材料处于非密实化，且随着倾斜角的增大，非密实化部分逐渐增加。这主要是由于材料左侧先发生变形，形成变形带，导致材料右侧在冲击结束时仍未密实化。因此，随着冲击板倾斜角的增大，材料的能量吸收逐渐减弱。而方法2 在变形初期反映的是局部应力的激增，与方法1 相比，在计算平台应力时得到了更高的数值。因此，使用方法2 得到的平台应力被高估。结合变形图与能量吸收曲线分析可知，方法1 得到的平台应力更适用于吸能工况。

3 结 论

采用有限元方法研究了内凹六边形蜂窝结构在斜冲击荷载下的动态力学响应，得到以下结论。

(1) 内凹六边形蜂窝结构在斜冲击与正冲击时的变形模式不同，在低速斜冲击下为局部变形，在中高速斜冲击下为整体变形，而在正冲击下均为整体变形。与正六边形蜂窝结构相比，内凹六边形蜂窝结构由于负泊松比效应的影响，变形模式产生延迟。在相同工况下，内凹六边形蜂窝结构的变形要晚于正六边形蜂窝结构。

(2) 基于无量纲时间参数t，提出了蜂窝结构在斜冲击下的应力时程表达式，该公式能够有效地反映蜂窝结构在冲击过程中从局部到整体的应力变化，可合理地反映蜂窝结构在斜冲击下的初始峰值应力，为蜂窝结构承载和稳定性的优化设计提供了理论依据。

(3) 结合变形图与能量吸收曲线，对比分析了两种方法得到的平台应力，结果表明，方法1 得到的平台应力更适用于吸能工况；方法2 在变形初期反映的是局部应力的激增，在计算平台应力中得到的数值更高。分析可知，当蜂窝结构在工程应用中首要考虑初始峰值应力时，方法2 更适用；但当首要考虑能量吸收时，方法1 更具有合理性。