基于改进蝴蝶算法和社会力模型的多出口疏散模型研究*

毛清华，余荣付，毛承成

(1.燕山大学 经济管理学院，河北 秦皇岛 066004;2.莫纳什大学 商学院，澳大利亚 墨尔本VIC 3145)

0 引言

随着经济发展，人们更加注重精神文化生活，每逢节假日，主要旅游景点及室内娱乐场所经常人满为患。即使受新冠肺炎疫情影响，2021年国庆出行人数也超过5亿人次[1]。在人群密集环境中，一旦出现紧急情况，无序疏散不仅会降低疏散效率，错失最佳疏散时间，还会导致碰撞和踩踏事件，造成二次伤害。如何在紧急情况发生后，提高疏散效率，并降低二次伤害发生率尤为重要。虽然疏散演习可提高行人对现场情况的熟悉程度，但需要投入大量人力物力财力，不能完全模拟突发情况下人群疏散真实效果。近年来,学者利用计算机建立不同需求场景进行仿真模拟，分析行人疏散的规律和状态，为疏散方案和建筑设计提供指导。

人群疏散模型[2]主要包括元胞自动机模型、社会力模型、格子气模型、流体动力学模型、Agent模型和排队论模型。其中，社会力模型应用最为广泛，其以连续运动方程为基础得到每个行人运动的连续动态坐标，不仅考虑行人与行人之间的作用力、行人与周围环境之间的作用力以及个体对于目标的自驱动力，并且重现疏散过程中“快即是慢”、“出口拱形”等现象[3]。随着疏散研究的不断深入，基本社会力模型不能精准描述实际疏散过程中行人的疏散行为。Liu等[4]考虑视角对个体运动的影响，在基本社会力模型中引入视觉影响因子;李昌华等[5]在基本社会力模型基础上,考虑行人疏散过程中运动方向及恐慌情绪和吸引力强度,再现行人疏散运动过程的自组织行为;Helbing等[6]指出行人运动过程中的期望速度会随其实现程度发生变化，反映行人紧张或不耐烦程度;Yang等[7]对于地铁站台的特定场景引入心理时间Ct，对行人期望速度变化进行修正。随着研究场景不断丰富，疏散情况越来越复杂，国内外学者开始在社会力模型中引入行人间聚合力[8]、危险源排斥力[9]、通风作用力[10]等参数，以精准描述行人的疏散运动行为。

上述研究为行人疏散提供有效的力学模型，但随着研究场景的不断变化，基本社会力模型对人群疏散的指导效率不断降低。为提高疏散仿真效率，可借助寻址优化算法实现疏散过程中的行人路径选择。Yang等[11]提出基于蚁群算法的客流分配建模方法，借用改进社会力模型预测候机区乘客的选择行为；韩雨烔等[12]结合遗传算法和社会力模型构建宏观-微观双层优化框架，分析出口宽度、疏散人员半径、疏散人员密度、出口布局对人群疏散效率的影响；李昌华等[13]利用粒子群优化算法建立多因子建筑疏散仿真模型，在基本PSO模型中引入正向驱动力、排斥驱动力、疏散人员恐慌程度等因子，改进局部寻优能力差和易过早收敛的问题；Zhao等[14]将改进动态路径规划人工蜂群算法与社会力模型结合，提出一种新的出口评估策略，在一定程度上平衡了距离和拥堵，成功模拟各种人群现象；Li等[15]针对大型多出口场馆的行人疏散问题，采用改进双策略自适应粒子群优化算法和亲和传播聚类算法进行行人疏散路径规划；魏娟等[16]改进基本社会力模型中影响行人运动的自驱力方向，结合粒子鸽群算法分析多出口环境下行人疏散问题；翟龙真等[17]在模型中引入模糊规则模拟行人运动速度，并结合广度优先搜索算法，建立基于排队理论的出口疏散机制，再现行人流自组织现象，提高疏散效率。

综上，随着疏散仿真研究不断深入，国内外学者对基本社会力模型做了部分改进，但忽略疏散过程中行人期望速度的变化，同时，在研究多出口疏散问题时，单独使用社会力模型对人群疏散的指导效率不断降低。蝴蝶算法[18]具有全局寻优能力强、原理简单、易于实现和鲁棒性强等优点，因此，本文提出融合社会力与蝴蝶算法模型，利用改进蝴蝶算法对行人进行路径规划，结合社会力模型将行人向出口驱动，该方法在多出口场景下能够有效地指导行人运动，真实模拟人群的疏散过程，提高疏散效率。

1 融合社会力与蝴蝶算法模型

1.1 社会力模型

1995年Helbing提出社会力模型，并基于牛顿第二定律构建社会力，把行人看作处于连续空间内的自驱动粒子，认为行人运动受自驱动力和与周边运动环境产生的物理力的共同作用。社会力模型如式(1)所示：

(1)

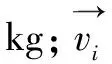
行人自驱动力如式(2)所示：

(2)

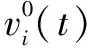
1.2 改进社会力模型

传统的社会力模型认为，人在疏散过程中期望速度不变，但实际情况中行人会根据距离目的地的远近以及当前所处位置的拥挤度产生焦急心理，进而想加快速度尽快摆脱现状，即当距离目的地较远时，行人会迫切到达疏散出口；当周围人数较多时，行人想尽快脱离拥挤人群，增加自己的期望速度。考虑到行人的焦急心理是累积过程，而Sigmoid函数与心理学中学习曲线类似[19]，因此，本文提出速度调节因子Pv，用以描述行人在疏散过程中期望速度的变化，如式(3)～(6)所示：

(3)

(4)

Pv(t)=(1+e-(δd(t)+γc(t)))-1

(5)

(6)

式中：(xi,yi)是行人i当前的位置坐标；(xj,yj)是目的地的位置坐标；d(t)是行人i在t时刻距离目的地的欧式距离，m；n是t时刻行人i附近的行人数量；s是行人i周围计算拥挤度面积，m2；c(t)是行人i在t时刻的拥挤度，人/m2；vmax是最大期望速率，m/s；δ和γ是取值[0,1]的调节系数。

改进的行人自驱动力如式(7)所示：

(7)

1.3 蝴蝶算法

蝴蝶算法是模拟蝴蝶觅食行为的自然启发算法，在蝴蝶群中散发低浓度香味的蝴蝶会被散发高浓度香味的蝴蝶吸引，并向高浓度蝴蝶移动。蝴蝶的香味取决于3个因素：感知形态、刺激强度、幂指数。蝴蝶香味浓度大小如式(8)所示：

f=cI∂

(8)

式中：f为香味大小，即香味被其他蝴蝶感知的强度；c是感觉模态；I是刺激强度，其值与蝴蝶适应度相关；∂是依赖于模态的幂指数。c和∂的取值范围为[0,1]。

蝴蝶算法包括2个关键步骤，即全局搜索阶段和局部搜索阶段。

1)全局搜索阶段：蝴蝶根据感觉到的其他蝴蝶香味浓度大小，选择向香味浓度高的蝴蝶移动。全局搜索如式(9)所示：

(9)

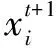
2)局部搜索阶段：当蝴蝶不能感知到其他蝴蝶散发的香味时，会选择随机移动。局部搜索公式如式(10)所示：

(10)

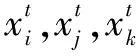
1.4 疏散场景下改进蝴蝶算法

本文利用蝴蝶算法进行行人路径规划，蝴蝶觅食行为与路径规划问题对应关系见表1。

表1 蝴蝶觅食行为与人群疏散参数关系

针对蝴蝶算法运算过程中容易产生搜索能力弱、寻优精度低以及易陷入局部最优等问题，本文提出自适应感知概率参数，以增强局部搜索和全局搜索间的平衡，并融合迭代局部搜索思想，在每轮迭代结束时引入迭代局部搜索策略，使算法快速跳出局部最优解，找到全局理论最优解。疏散场景下蝴蝶算法改进方法如下：

1)引入适应度函数

行人进行疏散时，高效利用多个出口可有效减少疏散时间。行人疏散过程中面临多出口选择时，一般选择离自己最近的出口进行疏散，但如果该出口处人数过多造成拥堵，行人会根据拥堵情况，判断是否应该选择其他出口尽快离开，即在最短时间内安全撤离是行人选择出口的首要因素。本文以疏散时间作为适应度函数的评价标准，即某个出口的适应度函数值越小，表示行人会以最短的时间完成疏散，则该行人就选择此出口进行疏散。适应度函数如式(11)所示：

(11)

式中：doornumi是选择i门行人的数量；doorout是出口的通行能力，人/s；disi是行人距离i门的距离，m；v0(t)是行人当前的期望速度，m/s；α，β是取值范围为[0,1]的调节系数。

蝴蝶算法中蝴蝶散发的香味与其适应度相关，即适应度值越小的位置，散发香味越大，表示该位置为最优点，容易吸引其他蝴蝶。香味公式改写为式(12)：

(12)

2)引入自适应感知概率

根据式(11)计算每个蝴蝶所在位置的适应度，再由式(12)得到每只蝴蝶散发的香味浓度，根据香味浓度从优到劣升序排序，根据式(13)给每只蝴蝶分配1个等级：

ranki=ii=1,2,3…,NP

(13)

式中：ranki为蝴蝶i解的排名；NP为种群大小。

散发香味浓度最高的蝴蝶(较好的解决方案)排序为1，散发香味浓度最低的蝴蝶(较坏的解决方案)排序最后。

分配给群体中每个个体的AP(感知概率)只取决于其在个体排名中的位置，与其散发香味的浓度值无关。对于每只蝴蝶，在APmin和APmax之间，根据其排列顺序选择AP值，如式(14)所示：

(14)

式中：APmin，APmax分别表示AP的最小值和最大值，本文设置APmin=0.1，APmax=0.8；DAPi为自适应感知概率。

由式(14)可知，AP值随蝴蝶个体排名上升而增加。散发香味浓度最高的蝴蝶个体排在第1位，其DAP值最小，散发香味浓度最低的蝴蝶排在最后一位，其DAP值最大。散发香味浓度高的蝴蝶高概率会进行局部搜索，而散发香味浓度低的蝴蝶进行全局搜索。对于每只蝴蝶，根据其DAP值，采用局部或全局搜索策略，如图1所示。

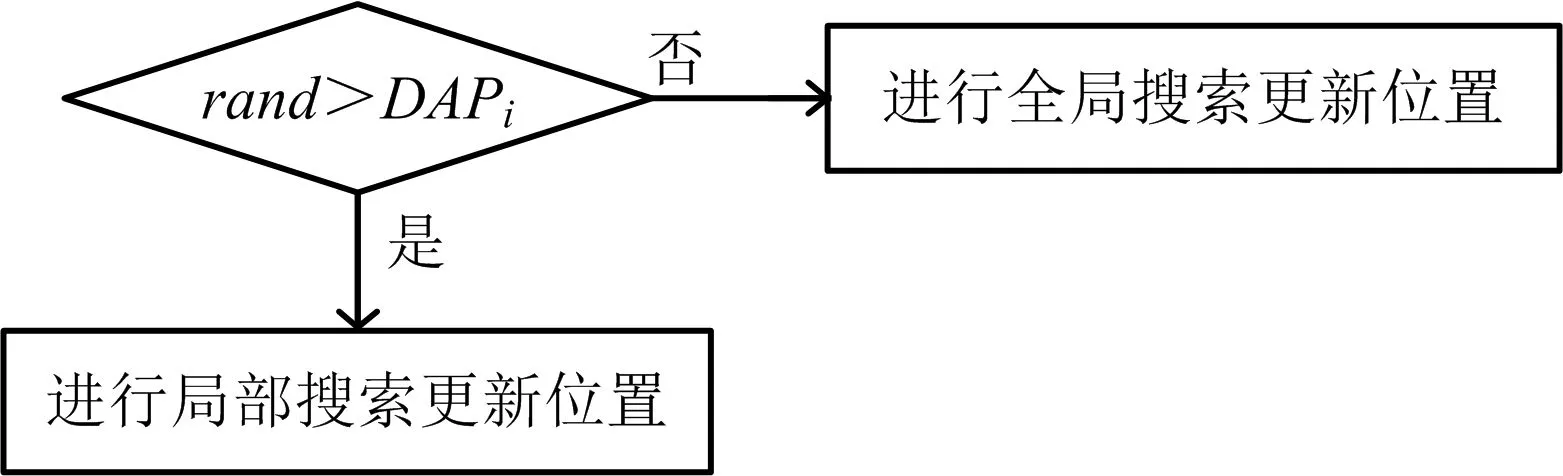
图1 判定搜索策略

3)融入迭代局部搜索算法

迭代局部搜索算法是一种简单有效的元启发式算法，原理是先扰动局部最优解以获得1个中间状态，然后重新搜索上述中间状态以获得全局最优解。该算法能快速跳出局部最优，找到全局理论最优解，因此，蝴蝶算法可以在每次迭代结束之前加入迭代局部搜索算法，提高跳出局部最优解的能力，并加快算法的收敛速度。基本求解步骤如下：

步骤1：对当前最优值x*进行扰动，得到中间状态x**，如式(15)所示：

x**=x*×rand()

(15)

式中：rand()为[0,1]之间的随机数。

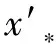
步骤4：输出最优解，结束算法。

1.5 模型求解步骤

根据上述描述，给出基于改进的社会力模型和蝴蝶算法求解多出口环境下的优化方法，具体包括以下7个步骤:

步骤1：初始化种群个数n、最大迭代次数N、个体位置xi以及相关参数，t为当前迭代次数。

步骤2：根据式(11)和式(12)，求出每只蝴蝶适应度值以及香味感知量函数值，根据蝴蝶发出香味大小按式(13)排序，并记录散发香味最浓的蝴蝶位置x*。

步骤3：判断个体搜索方式，按照式(14)计算每只蝴蝶的自适应感知概率DAPi，如果rand>DAPi，利用式(10)进行局部搜索计算，否则利用式(9)进行全局搜索计算。

步骤5：更新每只蝴蝶的位置xi，并计算新位置处蝴蝶散发香味和个体适应度值。

步骤6：如果当前迭代次数t

步骤7：利用改进社会力模型驱动个体向最优解运动。

2 仿真实验与分析

基于本文建立的人群疏散模型，得到2出口和4出口场景下仿真模拟示意如图2所示。疏散场景的疏散空间均为20 m×20 m，出口宽度为2 m，出口位置位于各边界中间位置。

图2 2出口和4出口场景下仿真模拟示意

仿真实验参数设置：行人半径r=0.25 m，行人质量m=65 kg,期望速度取值0.5～1.5 m/s，挤压力参数k=1.2×105kg/s2，摩擦力参数κ=2.4×105kg/(m·s)，行人之间以及行人与障碍物之间的作用力强度A=2 000 N，行人之间以及行人与障碍物之间的作用力范围B=0.08 m，出口处计算拥挤度的面积S=10 m2,出口通行能力dooroutmax=5人/s。

2.1 改进社会力与基本社会力模型仿真对比

为研究改进社会力模型与基本社会力模型的差异性，在图2(b)场景下进行模拟仿真，仿真结果如图3所示。由图3可知，改进社会力模型考虑距离出口的远近及行人所处位置拥挤度对期望速度的影响，行人在运动过程中会根据自身位置调整期望速度，相较于假设期望速度不变的基本社会力模型，疏散效率显著提高。

图3 改进社会力模型分析

2.2 不同初始人数的疏散仿真分析

为检验多出口场景下本文模型的行人疏散性能，分别在2种场景下针对不同数量的行人进行疏散仿真。不同出口条件下疏散人数随时间变化如图4所示。由图4可知，随疏散时间增加，2种场景的室内人数平滑下降，为避免行人大量集聚在某个出口造成堵塞而其他出口相对空闲，导致疏散人数激增或激减现象，应均衡地利用各个出口。说明本文模型在不同出口数量的疏散场所以及不同初始数量行人的疏散中起到指导作用。

图4 不同出口条件下疏散人数随时间变化

2.3 不同算法的疏散仿真对比分析

为验证本文算法的实用性，与广泛用于路径规划的PSO(粒子群优化算法)、ABC(人工蜂群算法)、GA(遗传算法)以及MBO(蝴蝶算法)进行仿真比较。基于图2场景参数，采用不同算法对不同出口场景下的疏散进行仿真模拟，假设2个场景容纳人数n=500，仿真结果如图5所示。

由于本文模型考虑行人疏散过程中期望速度的变化及添加出口选择策略，由图5可知，无论2出口还是4出口疏散场景，疏散时间均相对较短，在紧急情况下能够更好地模拟人群的真实疏散过程。随疏散出口数量增加，PSO、ABC、GA、MBO模型的疏散效率不断降低，在处理多出口疏散场景时，本文模型适用度较高。

图5 不同出口条件下各算法的疏散结果对比

2.4 疏散方法的对比实验

为验证本文模型的疏散效率，将其与文献[14]所提方法基于同一场景和相同参数进行仿真模拟。根据文献[14]得到3种算法在2，4出口场景下疏散不同人数所需时间，并将其与本文模型的疏散时间进行对比，如图6所示。由图6可知，在不同疏散场景下，疏散不同人数人群时，本文方法可为行人选择合理的路线，缩短疏散时间，这是因为本文模型优化了蝴蝶算法收敛速度慢、易陷于局部最优等缺陷，且在社会力模型中引入速度调节因子Pv以调节运动过程中的期望速度。文献[14]所提方法假设期望速度恒定，并未考虑行人处于不同位置状态导致期望速度发生变化，进而加快运动速度的实际情况。

图6 不同疏散场景下不同模型疏散结果对比

3 结论

1)在基本社会力模型中引入速度调节因子Pv，使行人在疏散过程中期望速度随疏散状态不断变化，使仿真更贴合实际疏散情况，提高行人疏散模拟精度。

2)采用蝴蝶算法，模拟行人在疏散过程中的路径选择，针对该算法后期收敛速度慢的缺点，引入自适应感知概率参数增强局部搜索和全局搜索之间的平衡，加快算法收敛速度；针对该算法易陷于局部最优的缺点，在每轮迭代结束时引入迭代局部搜索策略，扰动局部最优解获得中间状态，并重新搜索上述中间状态得到全局最优解，提高算法寻找最优解的精确性。

3)本文模型在不同出口数量的疏散场所以及不同数量行人的疏散场景中，能够起到有效的指导作用，且在多出口疏散场景下相比于其他典型的智能算法，能够更有效地模拟行人疏散过程，为疏散方案和建筑设计提供参考。