气相进料对隔板精馏塔优化设计的影响

2022-08-10刘会影贾胜坤罗祎青袁希钢

化工学报 2022年7期

刘会影，贾胜坤，2，罗祎青，2，袁希钢，2，3

（1 天津大学化工学院，天津 300354；2 天津大学化学工程研究所，天津 300354；3 化学工程联合国家重点实验室（天津大学），天津 300354）

引言

隔板精馏塔由完全热耦合塔发展而来[1]，将完全热耦合塔的两个塔整合在同一个塔中，中间以一块隔板隔开，将其分成预分馏塔和主塔，当忽略壁间传热时，隔板塔与完全热耦合塔热力学等效[2]。对于三组元精馏，隔板精馏塔减少了中间组分的返混，具有更高的热力学效率[3-7]，其次将预分馏塔和主塔整合在同一个塔壳中，减少了冷凝器或再沸器的数量，因而节约了设备费用。故相比传统流程，隔板塔能耗以及设备投资均可显著降低，是十分具有前景的精馏方式。

但由于隔板精馏塔采用了预分馏塔和主塔耦合结构，相比于传统精馏塔增加了液相分割比、气相分割比以及多个精馏塔段塔板数等决策变量[8]，因此最优化设计和操作控制变得更加复杂、困难[9-12]。研究表明，隔板精馏塔所具有的操作弹性可以适应进料流量和组成在一定范围内变化[13-15]。然而进料的热状态，即进料的气相分率会对塔内气、液两相流率有显著影响[16-17]，与通常的饱和液相进料相比，含有气相的进料会导致隔板精馏塔各个塔段的气、液相负荷显著不同，会远超出隔板精馏塔的弹性范围。然而考虑这一影响的隔板精馏塔优化设计方法研究尚未见报道，其主要原因在于问题的复杂性所导致的模型化及其求解上的困难。

在隔板塔优化设计中，液相分割比作为操作中可自由调节的变量加以优化，但气相分割比在操作中则由隔板两侧压降自发调整[18-19]，而这一调整不仅取决于隔板位置，还取决于隔板两侧的操作对气相的阻力[20]。这一操作阻力在塔内件确定后取决于塔内水力学条件，因此隔板最优位置的确定必须考虑水力学条件的影响。与此同时，在采用严格模型进行精馏过程最优化计算时，牛顿法计算的收敛性对初始点的苛刻要求是困扰这一类方法的主要问题，加之隔板精馏塔有众多整数变量(各塔段塔板数)以及水力学模型的加入，基于严格模型的隔板精馏塔最优化更加困难。

目前已将多种方法应用在隔板塔最优化计算中。有研究采用序贯优化法对隔板塔进行优化[21]，将离散变量与连续变量分开优化，这种方法忽略了变量间的相互作用，无法保证得到最优解；同时也有研究引入粒子群算法[22]、遗传算法[23]等随机优化算法来实现隔板塔所有变量的同时优化，但需要大量迭代从而导致计算瓶颈；接着有研究采用代理模型代替隔板塔严格机理模型解决优化问题[24]，缩短了优化时间，但对代理模型精度要求较高。

针对精馏过程最优化问题，本课题组前期研究[25-26]发展了一种基于虚拟瞬态延拓法的严格平衡级精馏模型，该模型引入动态方程和与之相关的虚拟持液量，得到较易于求解的微分代数方程组(DAE)，进而将牛顿法初始点问题转化为DAE求解中的初始条件问题，有效避免了牛顿法初始点收敛失败问题，提高了最优化计算收敛的稳健性。Li等[20]基于上述方法，实现了考虑塔板水力学的精馏塔结构变量和操作变量的同时优化。

本文采用上述虚拟瞬态延拓法的严格平衡级精馏模型[25]以及考虑塔板水力学的精馏塔结构变量和操作变量的同时优化方法[20]，建立针对具有不同气相分率进料的隔板精馏塔的最优化方法，并通过最优化计算考察进料中气相分率对隔板位置等结构参数的影响，通过严格模拟计算定量分析隔板不同位置的优势以及产生这种优势的原因。

1 模型和最优化方法

1.1 基于虚拟瞬态延拓法的严格平衡级精馏模型

平衡级模型方程主要由物料平衡方程(M)、相平衡方程(E)、归一化方程(S)和能量平衡方程(H)构成，简称MESH 方程。本课题组研究[26]提出的基于动态模拟和虚拟瞬态延拓法的严格精馏模型将质量平衡方程和能量平衡方程以微分方程形式表示，建立的MESH方程如下。

物料平衡方程(M)：

式中，CV、CL为常数，取值1800 h-1。

1.2 塔板水力学模型

本文以筛孔塔板为例建立隔板精馏塔水力学模型，对于其他形式的塔板或填料可参考本节的建模方法用相应的水力学公式加以替换。筛孔塔板压降计算采用Bennett 等[27]提出的筛板压降公式，其单板压降主要由三部分组成，即板上清液层高度引起的压降：

1.3 隔板位置参数模型

隔板塔中由于隔板的存在出现非圆形塔板，但由于缺乏非圆形塔板的水力学模型，本文采用Dejanović 等[28]的做法将非圆形塔板等效成圆形塔板，隔板左侧和右侧的塔截面积分别表示为：

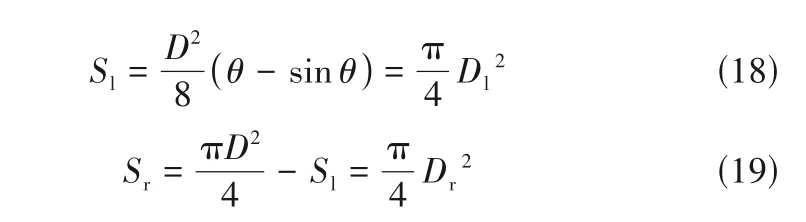
式中，Sl、Sr分别为隔板左、右两侧的面积；θ为隔板两端与圆心的夹角，其定义如图1 所示；Dl、Dr分别为隔板左、右两侧等效圆形塔板直径。

定义描述隔板位置的参数为β，表示预分馏塔一侧面积占全塔横截面积的比例。

当β=0.5 时代表隔板位于中间位置，否则偏向预分馏塔(0＜β＜0.5)，或主精馏塔(0.5＜β＜1)一侧。

1.4 最优化问题

本文应用到的隔板塔设计结构如图2所示。图中塔段Ⅱ、Ⅳ分别为预分馏塔的精馏段和提馏段；塔段Ⅰ为公共精馏段，Ⅵ为公共提馏段，二者与塔段Ⅲ和Ⅴ共同组成主塔。

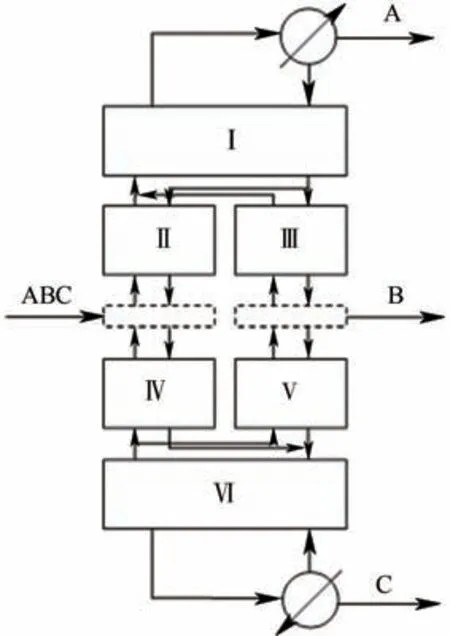
图2 隔板塔设计示意图Fig.2 Schematic diagram of the DWC model

本研究以年度总费用(TAC)为评价指标，优化变量包括隔板精馏塔的6 个塔段(图2)的塔板数Ni(各塔段塔板数确定即确定进料位置及侧采位置)、回流比(RR)、再沸比(BR)、侧采分率(侧线采出塔板上侧线采出液相流量占此板液相流量的比例Sf)、气相分割比(进入预分馏塔一侧的气量占总上升气量的比例RV)、液相分割比(进入预分馏塔一侧的液量占总下降液量的比例RL)、塔顶压力(P)、塔径(D)、隔板位置参数(β)。约束条件为：

(1)塔顶、塔底及侧采产品纯度要求；

(2)冷凝器和再沸器换热温差不小于10℃；

(3)隔板两侧的塔段压降相等，即

本文塔板数的优化采用Dowling 等[30-31]提出的绕流效率方法，以及Li等[20]的隔板精馏塔优化方法，采用绕流效率参数εj对任一预设的塔板j存在与否进行描述，即εj趋近于1或0分别表示该塔板趋于存在或不存在。塔段内绕流效率的加和即为该塔段塔板数。

隔板塔优化过程如图3所示。首先对各决策变量在其变化范围内给定初值；接着根据分离物系，确定适宜的塔板或填料形式，选择对应的水力学关联式及塔板或填料参数；然后基于考虑塔板水力学的精馏模型，采用虚拟瞬态模型辅助的稳态优化算法完成所有变量的同时优化，稳态优化使用Aspen Custom Modeler 中的Hypsqp求解器完成。为避免陷入局部最优解，可每次以不同的初值进行优化。最终在满足MESH 方程及上述约束的条件下，得到满足最小TAC的最优决策变量组合。

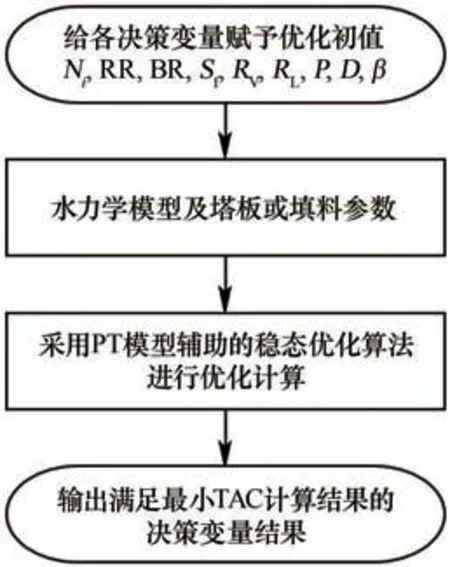
图3 隔板塔设计框图Fig.3 Design framework of a DWC

1.5 TAC计算模型

本研究优化目标采用年度总费用(TAC)，参考Douglas[32]提出的年度总费用评价方法，并做出部分修正，其主要包括两部分：设备费用和操作费用。设备偿还期选择3年。

2 结果与讨论

本研究选取苯(A)、甲苯(B)和对二甲苯(C)三元混合物进行隔板精馏塔设计，讨论进料中气相分率对隔板位置的影响。进料条件和产品要求见表1，物性、汽液平衡以及焓值的计算采用Chao-Seader热力学模型[33]，采用1.2节中的水力学模型计算塔板压降。

表1 进料状况和产品要求Table 1 Feed condition and product request

2.1 气相进料与液相进料优化结果比较

由于本文考虑在进料中含有气相时隔板位置变化规律及其对隔板塔的影响，故首先分析进料气相分率分别为0和1两种进料点下隔板塔的操作性能和结构设计。相应的进料状况和产品要求列于表1中。

首先对饱和液相进料情况(即γf=0)进行隔板精馏塔优化设计，得到的该进料条件下最优结构参数和操作参数如表2 中工况a 所示。如果将该隔板精馏塔用于气相进料操作，即结构参数不变，仅将进料气相分率γf由0 变为1，计算发现，如进料流量和产品要求以及操作压力不变，无论如何调节操作参数，塔段Ⅰ、Ⅱ、Ⅲ和Ⅴ无法满足水力学条件，即气、液相负荷超过了泛点上限。这是因为，表2中工况a的隔板精馏塔是考虑了塔板水力学的结构和操作参数的最优设计，因此进料中气相分率变化导致操作参数仅允许在设计裕度所允许的范围内变化，如超出该范围则会因液泛导致无法正常操作。图4(a)和(b)为两种进料条件下各个塔段压降变化情况，表明将工况a设计的精馏塔用于气相进料时塔段Ⅰ、Ⅱ、Ⅲ和Ⅴ由于发生液泛，其压降大幅增加[图4(b)]。

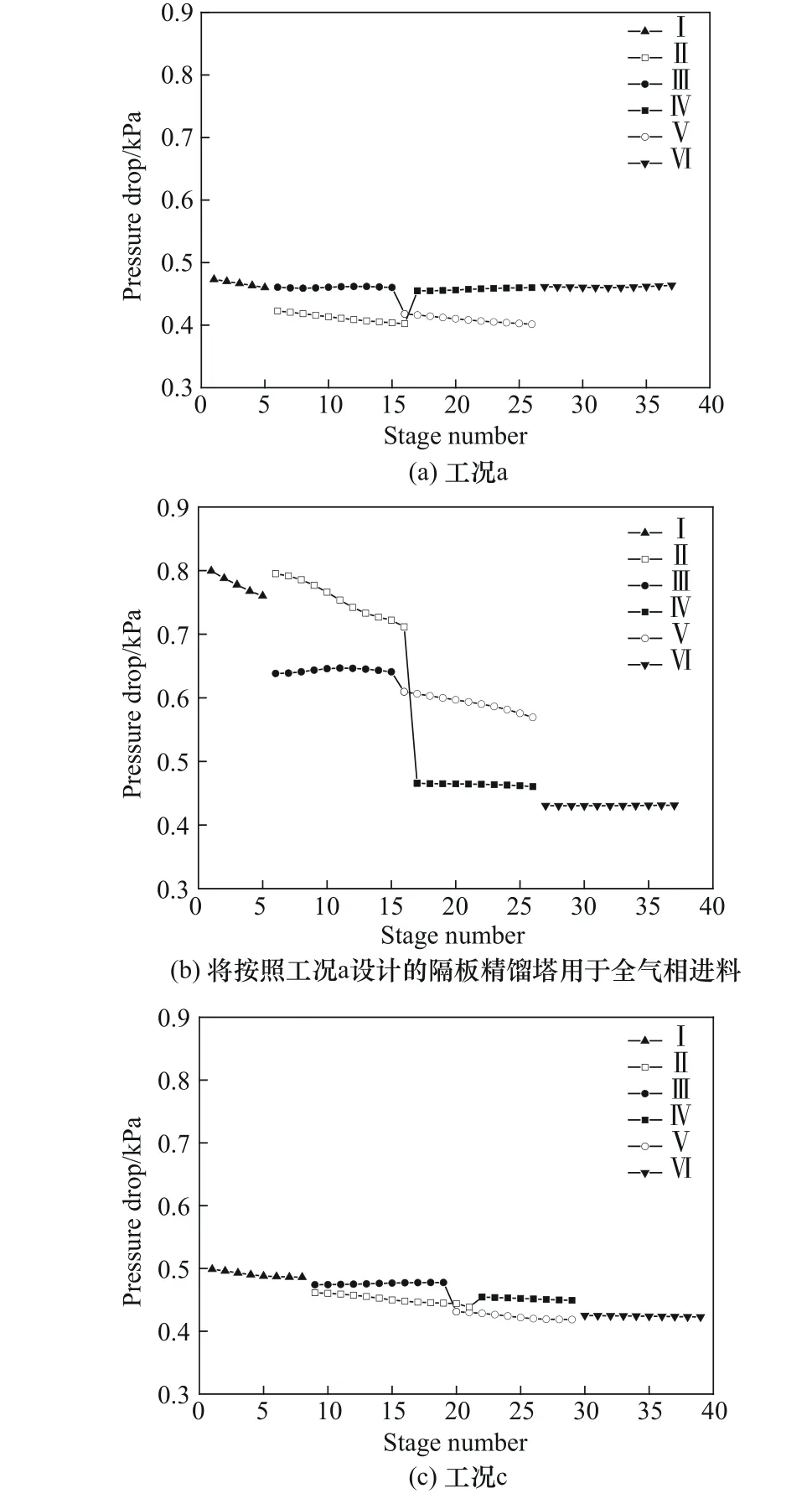
图4 隔板精馏塔塔板压降分布Fig.4 Tray pressure drop distribution of DWC

此时，为了避免液泛实现可行操作，必须降低处理量。故本文将进料流量与操作参数一同进行优化，获得可行的操作如表2 工况b 所示。比较表2中工况a和b表明，当使用全液相进料设计的隔板精馏塔处理全气相进料时，如产品要求和操作压力不变，则需要将进料流量由500 降为257 kmol/h。因此，虽然实现了可行操作，但如表2所示单位处理量的费用(TAC/F)显著增加。

表2 不同进料条件下的设计变量和相关费用Table 2 Design variables and related costs with different feed conditions

上述分析表明，对于本文给定的体系，将按照液相进料设计的隔板精馏塔直接用于全气相进料是不可行的，主要表现为多个塔段气液相负荷过大引发液泛。与传统精馏塔不同，隔板精馏塔内各个塔段的负荷与隔板的位置密切相关，因此本文将隔板塔中的隔板位置(β)作为优化变量是必要的。

为此针对全气相进料(γf=1)对隔板精馏塔，包括隔板位置等结构参数，重新进行最优设计，结果如表2 工况c 所示，其各塔段的压力降如图4(c)所示。比较表2 中的工况a 和c 可知，全气相进料的隔板精馏塔隔板位置等最优结构参数明显有别于全液相进料的情况，塔径略有增加，但隔板位置参数变化显著，β由原来的0.6376 增加到0.8221；同时因进料为气相，所需回流比以及塔段Ⅰ、Ⅱ和Ⅲ板数有所增加，塔段Ⅳ、Ⅴ和Ⅵ板数有所下降，冷凝器负荷增加，再沸器负荷减小。而总费用(TAC)和单位进料流量总费用(TAC/F)均略小于工况a。应指出，与液相进料相比，气相进料带有相变热因而焓值更高，如果不考虑进料相变所需能耗，气相进料的精馏过程能耗应明显低于液相进料。如表2 中工况a 和c 所示，气相进料精馏过程的操作费相较液相进料降低36.71%，导致TAC/F降低23.36%。比较表2 中工况b和c表明，如果用按照液相进料设计的隔板精馏塔处理气相进料，其处理单位进料的精馏塔总费用(即TAC/F)比最优设计(即工况c)高出60.87%。

若考虑单位进料由γf=0变为γf=1相变所需能耗，处理此部分能耗所需操作费为0.2301×104USD/kmol，将其加入TAC/F中，工况b和工况c结果变为0.6170×104和0.4706×104USD/kmol，工况b较工况c依然高出31.11%。由此说明采用液相进料设计的隔板精馏塔直接处理气相进料需要大幅降低进料量，同时十分不经济，故需要针对气相进料重新设计隔板精馏塔。

2.2 进料气相分率对总费用的影响

为研究进料气相分率的影响，将进料气相分率从0变化到1，以0.2为变化步长，在每一个进料气相分率下都对偏心直隔板结构的设备参数和操作参数进行同时优化，得到的最小TAC 以及设备费用和操作费用如图5所示。

图5显示，随着进料气相分率的增大，设备费增加不足10%，但操作费降低36.73%，导致TAC 降低23.33%。同时结合表2 数据，气相进料导致塔顶回流比增加，冷凝器负荷增加，同时塔段Ⅰ和Ⅱ所需板数有所增加，因而影响图5中的设备费用，这是由于随着进料气相分率的增加导致进入精馏段(即进料以上塔段)的气相中较重组分分率增加，因而需要更大的塔板数和较大的回流比。这虽然导致冷凝器公用工程费用的增加，但由于再沸器所用的公用工程价格显著高于冷凝器的价格，再沸器操作费用减小程度显著大于冷凝器增加程度，最终使得操作费用降低。故进料气相分率增加时，操作费用的减小是TAC 减小的主要原因。若考虑进料相变所需能耗，图5 中气相进料处TAC 与操作曲线上移，气相进料费用高于液相进料。此部分能耗若由热量回用等其他能量利用手段提供，气相进料依然为最经济的选择。

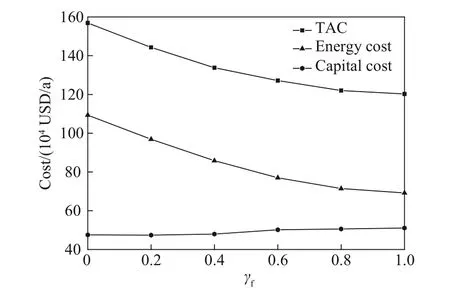
图5 不同进料气相分率下费用变化Fig.5 Costs with different feed vapor fraction

通过优化设计计算，随着进料气相分率的变化，隔板精馏塔的最佳隔板位置如图6 所示。可以看出随着进料气相分率不断增大，隔板位置参数β也不断增大，即隔板逐渐向主塔一侧移动。这是因为γf越大，进料点以上气相流量越大，隔板两侧气量差异越来越明显，如果隔板两侧对气相流动的阻力变化不大，则β随γf的增加而增加是隔板两侧达到压降相等的必然结果，即气量越大，所需塔截面越大。

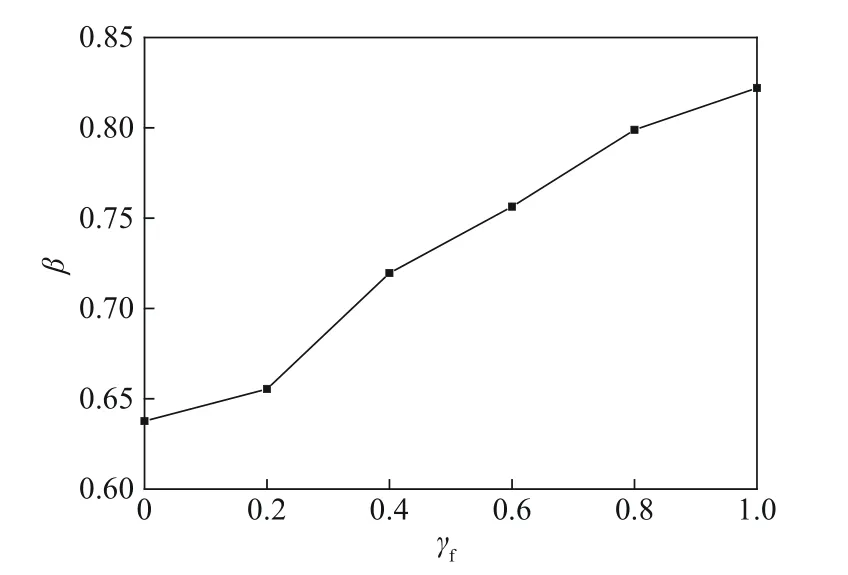
图6 不同进料气相流率下隔板塔隔板位置参数变化Fig.6 β value under different feed vapor flow rate

2.3 隔板位置对总费用的影响

Ge等[14]和敖琛等[15]研究表明，隔板精馏塔的气相分割比是决定总费用的重要参数，同时存在一个与最佳气相分割比唯一对应的最佳液相分割比。在隔板精馏塔的操作中，气相分割比直接受隔板位置参数β的影响。为了探明隔板位置对总费用的影响，本文选取表2 工况c 的塔板数和塔径以及γf=1 时的进料条件，针对工况c 的最优β值(即β=0.8221)邻域内多个不同的β值，仍以TAC最小为目标函数分别对其他操作参数进行优化，以考察隔板位置对TAC 影响的灵敏度，结果示于图7。图7表明，在给定的进料气相分率下，存在一个最优隔板位置使TAC 值最小。当β从最优位置减小时，也就是隔板向预分馏塔一侧移动，TAC变化较为平缓，当β从最优位置增大时，隔板向主塔一侧移动，TAC变化较为显著。图8描绘了隔板位置变化时最佳气相分割比以及与之对应的最佳液相分割比的变化情况。图中显示，随着隔板位置参数β值的增大，气、液相分割比逐步增大，但气相分割比的增幅较液相分割比剧烈，说明隔板位置对气相分割比较为敏感。同时发现随着β值的增大，气、液相分割比呈非线性增加，且增加率随β值的增大而增加，这解释了图7当β值大于其最优值时TAC的增加更为显著这一现象。

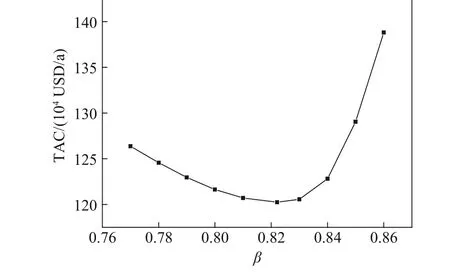
图7 TAC值随隔板位置变化Fig.7 TAC varied with position of the partition

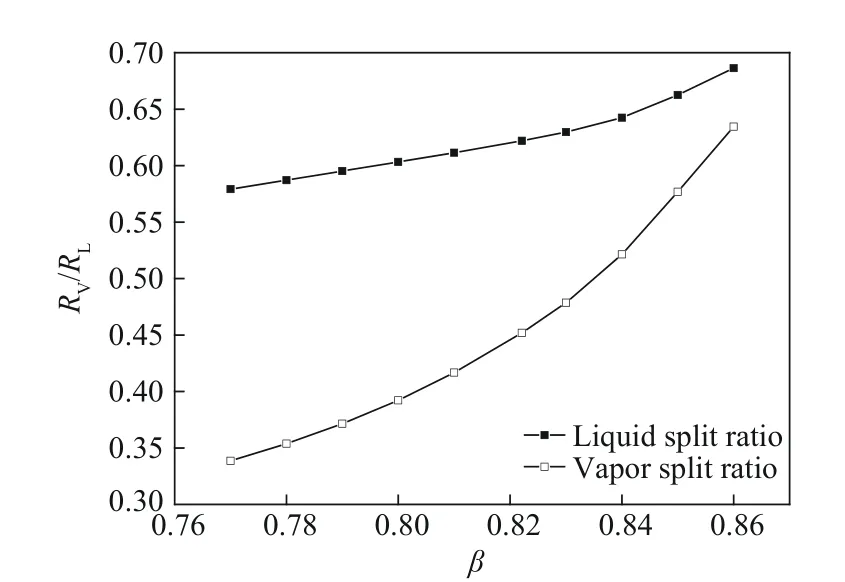
图8 气相/液相分割比随隔板位置变化Fig.8 Vapor/liquid split ratio varied with position of the partition

3 结论

本研究表明，对于隔板精馏塔，当进料由液相变为气相时，隔板精馏塔的最优结构具有显著差别，其中隔板在水平方向上的位置变化显著，对精馏过程的可操作性以及能耗具有重要影响。因此当进料热状况发生变化时，需要重新设计隔板精馏塔，其中隔板位置应相应改变。通过对不同进料条件进行优化可知，如不考虑进料相变所需要的能量，进料气相分率越大，精馏过程年度总费用会越小。若考虑进料相变所需能耗会使气相进料费用增加，为此可采用热量回用等手段降低能耗，这在实际工业应用中对于选择合适的进料条件具有重要的参考意义。

隔板精馏塔中隔板位置会影响关键设计变量，包括气、液相分割比。对于特定的气相进料，存在最优的隔板位置参数和气、液相分割比组合使得TAC最低。且随着进料气相分率从0变化到1，预分馏塔一侧气相流量增大，隔板逐渐向右侧移动保证隔板左侧有足够的空间容纳气液相进行传质传热，故对于进料条件的不同，要适当调整隔板位置以满足分离要求。

符号说明

A——换热面积，m2

C——与堰有关的系数

Cca——设备费用，USD

Cco——塔体设备费用，USD

Ccon——冷凝器设备费用，USD

Cep——公用工程单价，USD/GT

Cop——操作费用，USD

Creb——再沸器设备费用，USD

cV——孔口系数

Dmin——发生液泛的最小塔径，m

d——孔口直径，m