蒸汽冷凝近壁过渡区团簇演化特性

2022-08-10李雯兰忠强伟丽任文芝杜宾港马学虎

化工学报 2022年7期

李雯，兰忠，强伟丽，任文芝，杜宾港，马学虎

（1 大连理工大学化学工程研究所，辽宁大连 116024； 2 内蒙古北方重工业集团有限公司，内蒙古包头 014000）

引言

冷凝成核现象广泛存在于自然界及生产生活中，如车窗上的白雾，生物表面的结露[1-2]，以及工业领域中的热管理[3-4]、水汽捕集[5]、热电系统[6]、海水淡化[7-8]等。对成核过程的演化规律和机理的深入研究，不仅可以为冷凝过程的调控提供指导，还有助于完善蒸汽冷凝换热过程的基础理论。

关于成核过程的机制，1935 年，Tammann 等[9]提出固定成核中心假说，认为蒸汽在壁面冷凝时，气相中的水分子首先在壁面上的成核位点处核化。随后，研究者们通过大量的实验观察和理论分析[10-13]证明了该假说的合理性，但该假说并未描述蒸汽分子靠近壁面以及形成最小核化液滴之前所经历的物理过程，这也使得大部分针对凝结过程或核化过程的调控技术，主要关注在壁面微纳功能结构或成核位点的设计上。宋天一等[14]通过湿空气露点冷凝的可视化实验，发现冷凝表面上初始液滴尺寸分布符合对数正态分布，再结合分子团聚理论[15]，反演推知气相分子在壁面沉积之前已经在近壁空间中形成了团簇分布，从而提出了水分子在壁面上冷凝核化前会预先在近壁空间中团聚生成团簇的冷凝团聚物理模型。Lan 等[16]将上述冷凝团聚物理模型与滴状冷凝传热模型相联系，并分析了不凝性气体由于影响了团簇分布而极大影响了凝结换热效率的机制，通过将模型计算结果与文献中的实验数据对比进一步证实了模型的合理性。自此，近壁空间中的团簇作为成核前冷凝介质的存在状态开始进入研究者们的视野，对它的更为全面和深入的研究无疑是成核调控中的重要一环。

为了探究蒸汽冷凝核化前气相团簇的演化分布规律，并且考虑到传统的观测手段，如高速摄像和显微镜放大，难以观测发生在纳米和纳秒层面上的团簇演化，Lan等[17]利用瑞利散射原理，通过测量距离过冷壁面不同高度位置的散射光强来反映空间中团簇的分布，但鉴于瑞利散射光强受团簇尺寸与数密度的共同影响，更多的与空间团簇分布相关的细节，比如空间温度的变化以及团簇的形成机制还不清楚。近年来，越来越多的学者借助分子动力学（molecular dynamics,MD）模拟的手段来研究蒸汽在冷却表面上的成核物理过程，也鉴于对成核前近壁区分子团簇演化物理图景的缺乏，他们的工作也主要集中在壁面亲疏水性[18-20]，表面结构的形状、尺寸和排布[21-22]，壁面过冷度[22]，外场[23]，不凝气[24-25]等对壁面上的成核位置，团簇大小、数量、形状以及冷凝传热效果的影响。但不容忽视的是，对气相团簇分布演化的深入研究有望从“气液相变的初始状态”这个最早的阶段出发来完善成核过程的演化规律和理论，并为实际工程中的冷凝过程调控提供新的思路和指导。

分子模拟的尺度一般为纳米级，而从实验初步观测结果可以看出，近壁团簇演化分布范围为几百微米[17]，文献中常见的壁面-水冷凝的MD 模型无法直接用来研究整个近壁空间的团簇情况。因此，本文根据文献[17]中实验表明的冷凝达到稳态（定态）时，近壁空间形成一定团簇尺寸分布这一特点，从唯象角度，将处于近壁空间中某区域的近平衡态视为其中团簇处于热力学平衡状态，那么实际上该区域就处于一定的过饱和度，将相对宏观的近壁空间抽样成多个纳米尺度上的均相体系，并根据不同高度对应的团簇尺寸（也即过饱和度或蒸汽温度）不同，将近壁区团簇随离壁距离的分布曲线抽样成多个不同温度下的均相水体系冷凝模型，最后通过整合不同高度处的团簇演化特征，综合获得宏观近壁空间中的团簇演化构象和分布规律。在此基础上探究了蒸汽压力以及不凝气对近壁空间团簇分布的影响和作用机制。

1 近壁团簇分布规律MD 分析模型的构建

鉴于所研究物理问题是距离壁面几百微米的近壁空间中的团簇的演化分布，常规MD 方法很难实现。因此结合已有的理论和实验研究成果[17,26]，如图1所示，将近壁空间中团簇分布看作是唯象的，那么显然当冷凝过程达到稳态时，空间局部位置即可看成近平衡态，虽然团簇是可移动的，它可能会在壁面上徙动、分裂或蒸发，以及可能离开壁面或在近壁区扩散，但终将形成一个“稳定”分布，换句话说，近壁空间中某个位置对应一定尺寸及分布的团簇，而唯象角度可认为该位置的团簇处于热力学平衡。或者考虑这样的唯象分布状态，因为平衡态与过程无关，这样的团簇分布虽然可能是扩散等机制形成的，但也可以认为是水分子直接在近壁空间对应位置处于热力学平衡而得到的。再从另一个角度看，当冷凝过程处于定态时，壁面与体相间存在温差ΔT（即过冷度），但这种温差通常可理解为并非突变形成，而是在近壁较小空间中以某种渐变曲线方式形成。换句话说，近壁空间中有一个温度渐变的过程，因此与温度变化对应也将具有过饱和度变化的过程。特别要指出的是，通常在传热领域普遍接受近壁区（或者说边界层）温度是渐变的这个概念，但具体温度是如何渐变的，或者最需要强化的区域在哪里，并不清晰。因此可以将近壁区进行抽样分析，不同的过饱和度（用与蒸汽体相间的温差δT表示）代表不同的离开壁面的距离（但目前为止并不知道距离多远对应多大的过饱和度），通过分析不同δT（对应空间中不同高度位置）下团簇的演化分布特征来构建整个近壁空间的分布特征。这样一来，宏观尺度的过冷壁面上的非均相冷凝过程的近壁区，就可以借助分子动力学模拟通过均相体系在多个不同过冷温度δT下的演化来描述。

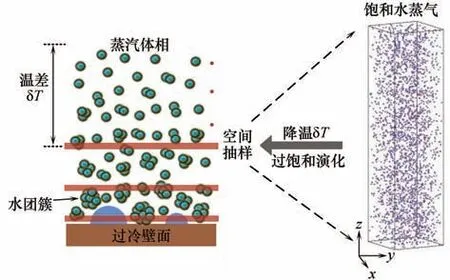
图1 近壁几百微米空间中团簇分布演化的研究方法的示意图和初始模拟体系的构建Fig.1 Schematic of research method for cluster distribution evolution in hundreds of microns space near subcooled wall and setup of the initial simulation system

根据上述分析来构建分子动力学模拟的具体模型，首先，选择TIP4P/2005模型[27]来表征水分子间的相互作用，它在描述与水冷凝相关的物性参数方面表现出较高的精度，在该模型中，H-O-H 平分线上距O 原子0.1546 Å(1 Å=0.1 nm)处设有一虚拟位点，带1.1128 e 的负电，两个氢原子分别带0.5564 e的正电，氢氧键长为0.9572 Å，键角为104.52°，相应的水分子间相互作用势的表达式如下：

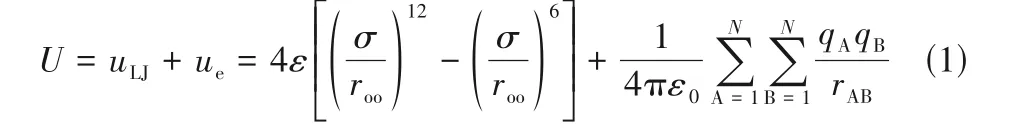
式中，U是水分子间的总势能，由两部分组成。第一部分的uLJ为短程范德华作用势，其中ε为势阱深度，代表两个原子间相互作用的强弱，σ为Lennard-Jones(LJ)势能等于0 时原子间的距离，对于氧原子有ε=0.1852 kcal/mol(1 kcal=4.18 kJ)，σ=3.1589 Å，roo为两个氧原子之间的距离。第二部分的ue为静电作用势，其中ε0为真空中的介电常数，qA为A 作用位点所带电量，qB为B 作用位点所带电量，rAB为A、B 两带电作用位点间的距离。因为水分子间的相互作用相比其他简单粒子多了静电力的影响，所以计算时更为复杂和费时，因此在构建初始模拟体系时，为了满足形成临界液核所需的分子数同时提高计算效率，选定初始温度T0为423 K的饱和水蒸气体系,且体系尺寸为lx×ly×lz=20 nm×20 nm×79 nm，再根据423 K下饱和水蒸气的密度为2.54 kg/m3，计算可得体系共包含2684个水分子，如图1所示。

2 模拟细节设置

选用大规模原子/分子并行模拟器（large-scale atomic/molecular massively parallel simulator,LAMMPS）进行分子动力学模拟，体系的x、y、z三个方向均设置周期性边界条件，运动方程的积分选用Velocity-Verlet算法，时间步长为1 fs。对LJ相互作用采取截断处理且截断半径设置为10 Å，长程静电力的处理选用PPPM (particle-particle-particle mesh)算法，模拟在NVT 系综下进行，使用Nose-Hoover 调温器来控制体系温度。

模拟具体分三个阶段进行，首先通过能量最小化对体系结构进行优化，防止在初始阶段局部受力过大而造成体系崩溃,优化的收敛标准根据文献[18]制定为直到体系中任何原子在任何方向上的受力小于1.0×10-6kcal/(mol·Å)。然后，进行第一次NVT系综下的模拟，控制体系温度为初始饱和水蒸气体系对应的饱和温度，即T0=423 K，弛豫总共150000时间步，即150 ps，让体系在初始温度下稍微平衡一下，形成一个初始饱和温度下正常的随机分布，温度的控制使用Nose-Hoover 控温方法。最后，进行第二次NVT 模拟，第一次NVT 模拟结束后，紧接着降低体系温度使Ti＜423 K，让水分子继续在Ti下演化直到平衡。为了对应距离壁面不同高度的位置，本文共模拟了九个体系，分别降低不同的温度δT=100,60,50,40,30,25,20,15,10 K，由于体系温度降低后水蒸气会进入过饱和状态，随着模拟的进行，体系中水分子团聚生成团簇，团簇不断生长、合并、分裂，直至达到对应温度下的平衡状态。使用Ovito、Vmd、Origin 以及Matlab 软件对模拟进行可视化观察以及数据的提取和分析。

3 结果与讨论

3.1 纯蒸汽条件下近壁空间中团簇的演化构象和分布规律

首先，以δT=50 K 体系的分子动力学模拟为例来进行简单说明，图2 显示了体系温度随模拟时间的变化，从图中可以看到体系初始温度和降低50 K后温度基本都在设置的温度值附近波动，表明模拟确实是按照所控制的温度进行的。图3(a)显示了随着时间的进行，体系能量E不断减小最终趋于稳定,这是因为随着模拟的进行，在过饱和的条件下，体系中的水分子逐渐凝结形成团簇并且团簇随时间在不断长大，期间也伴随团簇的合并与分裂,如图3(b)的模拟快照图所示。

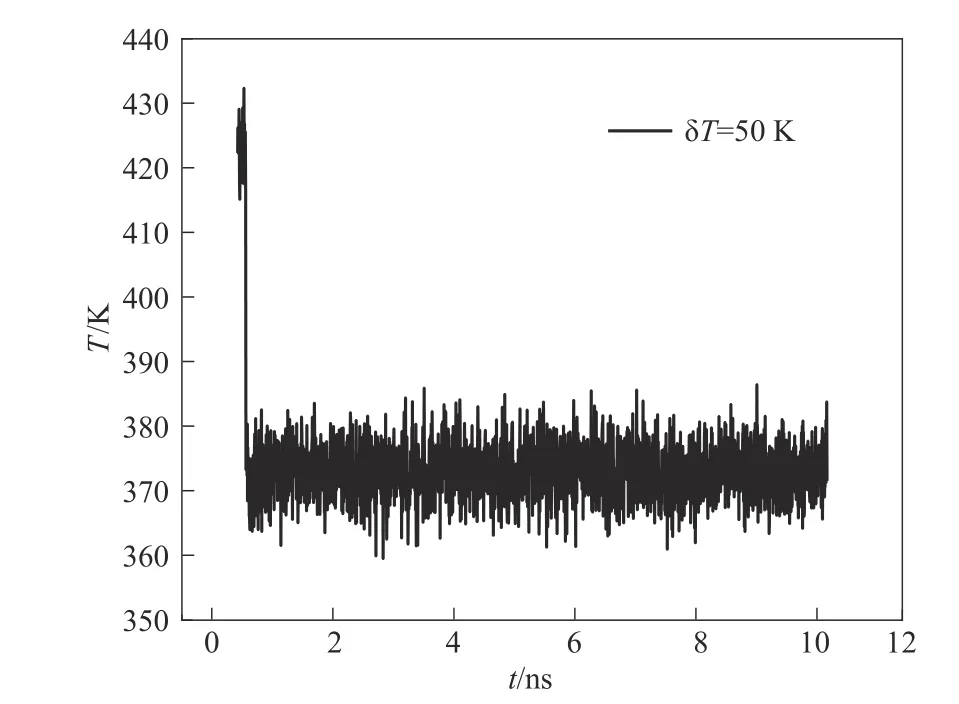
图2 δT=50 K体系的温度随模拟时间的变化Fig.2 Variation of system temperature with time for δT=50 K

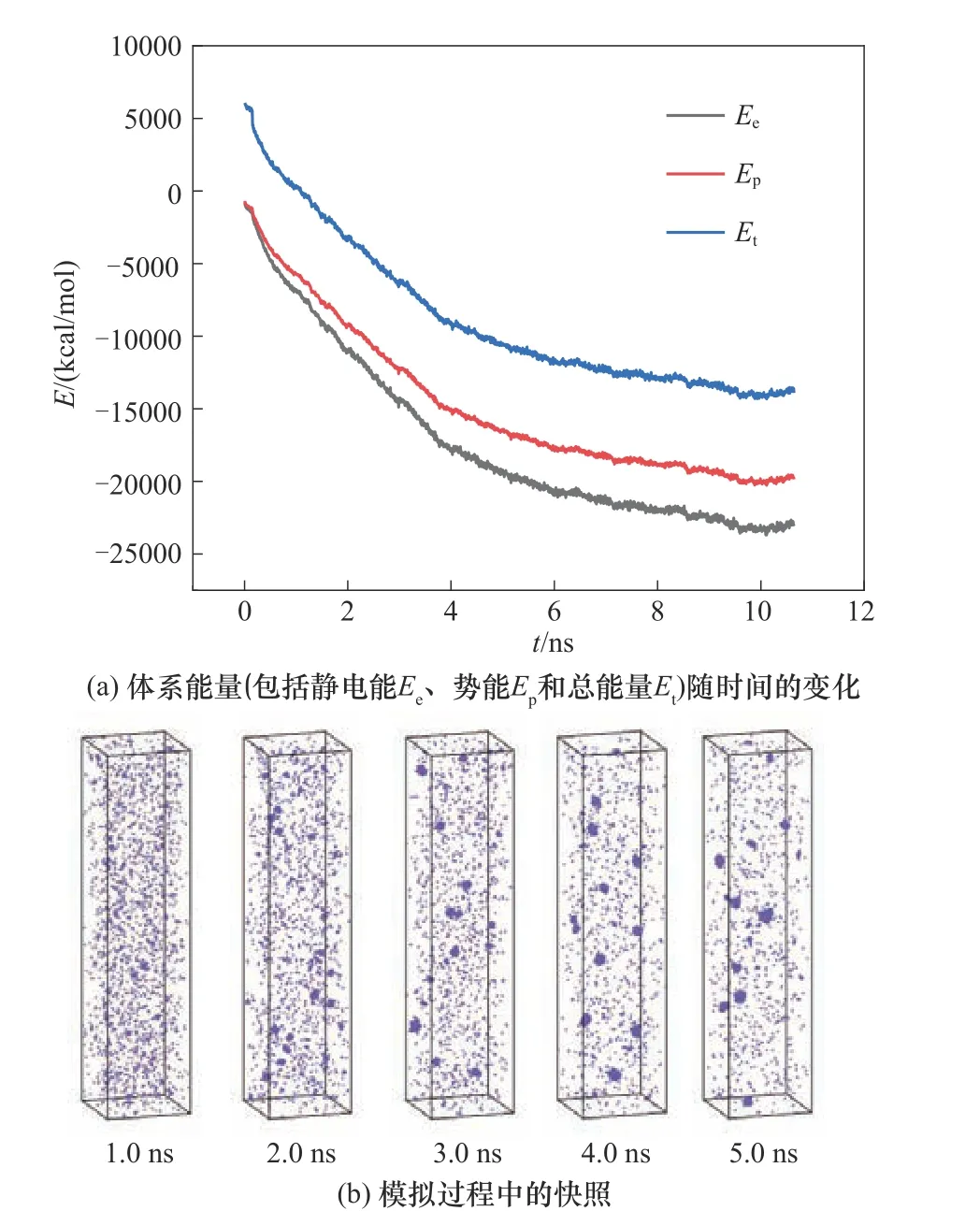
图3 δT=50 K时的模拟过程变化Fig.3 Variations during the simulation process for system of δT=50 K

为了比较不同δT体系中水分子的团聚情况，首先分析了不同δT体系的势能随时间的变化，如图4(a)所示，可以发现，对于所有的δT体系，由于水蒸气分子团聚形成团簇，体系势能值随时间不断减小，并最终达到稳定，势能曲线下降的快慢表明了团簇演化的快慢，可以看到δT越大，即距离过冷壁面越近，水分子团聚越快。随后，基于Stillinger距离判据[28]对体系中生成的团簇进行了识别和统计，当某个水分子中的氧原子与邻近团簇中的任何一个水分子中的氧原子之间的距离小于3.36 Å 时，认为该氧原子所在的水分子便属于该团簇，利用Matlab编程，通过读取模拟获得的轨迹文件，统计得到不同δT下不同时刻的团簇大小和数目信息，结果如图4(b)所示。从图中可以看到对于不同的δT总团簇分子数均随时间不断增大，最终稳定，并且δT越大，生成的团簇所包含的分子数越多。

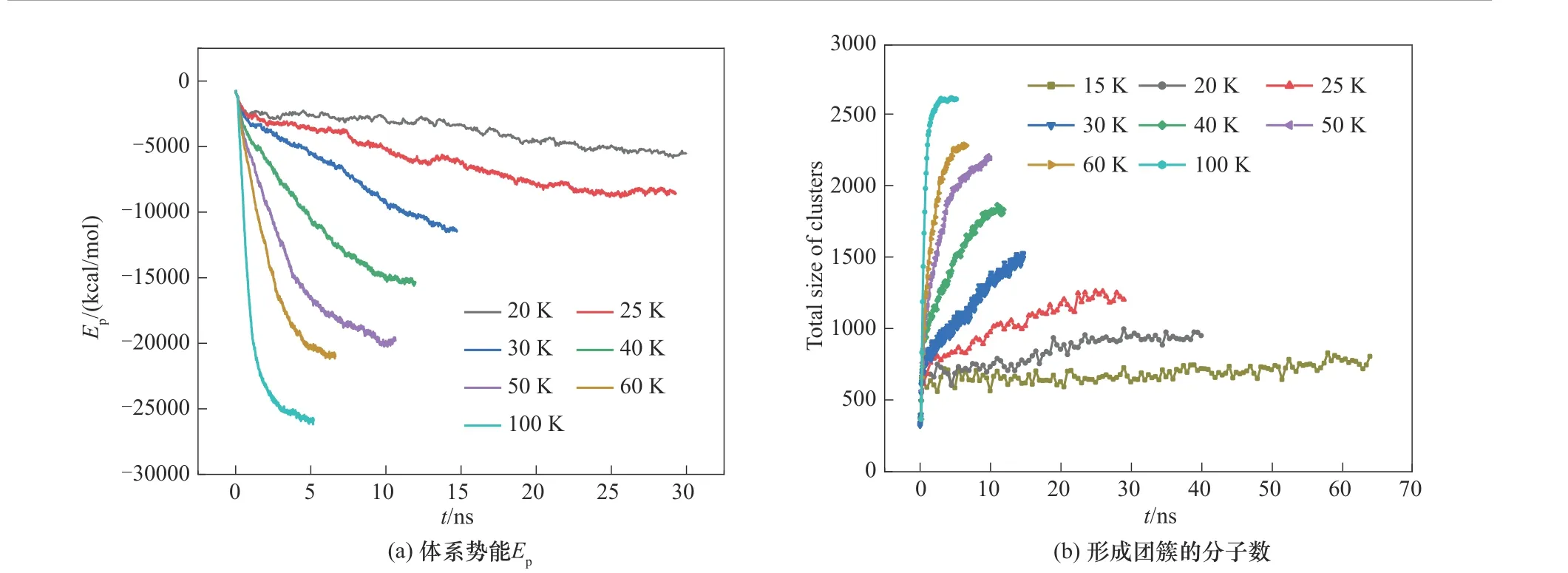
图4 不同δT体系中水分子的团聚演化Fig.4 Evolution of water molecules aggregation for different δT systems

采用Einstein 法[29]计算扩散系数，通过对粒子所走的路径进行一段时间的统计，计算得到相应的均方位移（mean square displacement, MSD），然后MSD对时间求导并除以6 得到扩散系数，其具体的计算过程如下：

式中，N为系统内总粒子数；ri(t)为第i个粒子在t时刻的位置矢量；D为扩散系数。通过模拟，统计得到MSD 随时间的变化曲线如图5 所示，从图中可以看到，δT越大，相应的扩散系数越小，δT为20、25 K体系的扩散系数相较其他δT更为接近。

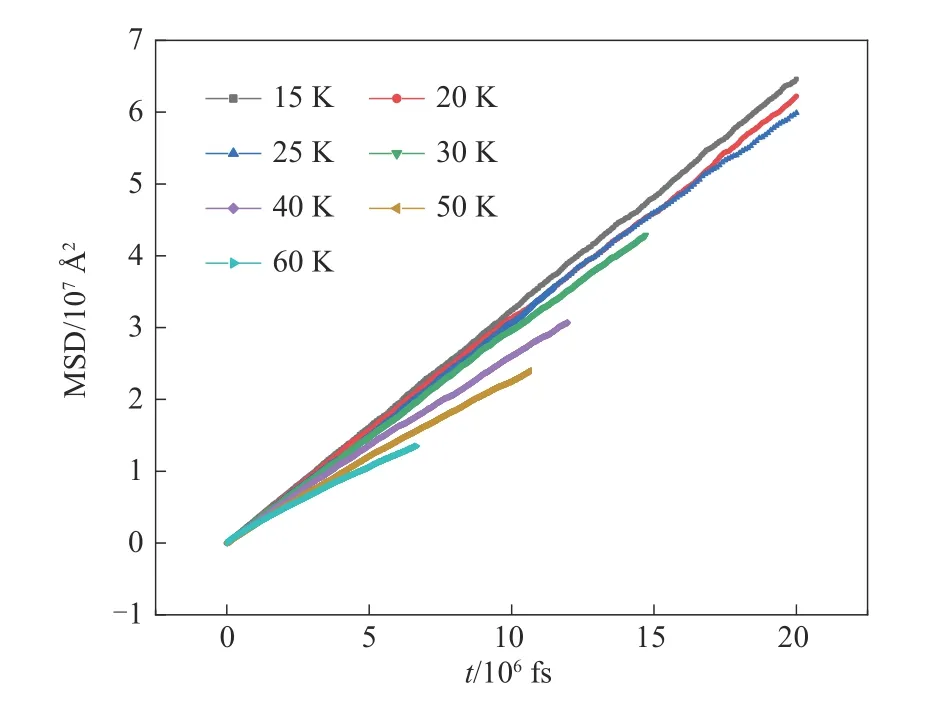
图5 不同δT体系的均方位移MSD随时间的变化Fig.5 Variation of mean square displacement with time for different δT systems

在以上对团簇分子数和扩散系数的统计结果的基础上，为了比较不同δT体系中的团簇分布演化的区别，需要找到某个时间节点或尺寸节点来作为比较基准，这里选取区域分布近平衡的时候，此时对于不同δT体系的“趋于平衡”的趋势与扩散趋势这两趋势的差值基本保持稳定，其中“趋于平衡”的趋势利用Boltzmann 分布，根据温度的分布来计算，扩散趋势则根据扩散系数来表征，据此经统计得到当最大团簇达到65 时，两趋势的差值基本一致，因此比较了最大团簇都为65 时各δT体系中的总团簇分子数以及扩散系数，结果如图6所示，从中可以看到对于初始饱和温度为423 K 的纯蒸汽冷凝，总团簇分子数和扩散系数均在δT=25 K 处出现一个明显的转折点，表明近壁空间温度从气相到壁面不是突变的，而是存在过渡的，且这个转折点正好反映了瑞利散射实验[17]中近壁平台区那个转折点，证实了团簇空间分布中一定存在特征转折点，由于δT的大小反映团簇尺寸变化的快慢，因此这个转折点恰恰就是近壁团簇分布的密集区的转折点，根据图6 的模拟结果，以转折点的δT=25 K（Ti=398 K）为界，δT＞25 K 的更靠近壁面的空间区域为团簇稠密分布的近壁区，对应文献[26]实验结果中距离壁面600 μm 以内的空间区域，δT＜25 K 的逐渐靠近气相主体的空间区域为扩散发展过渡区。

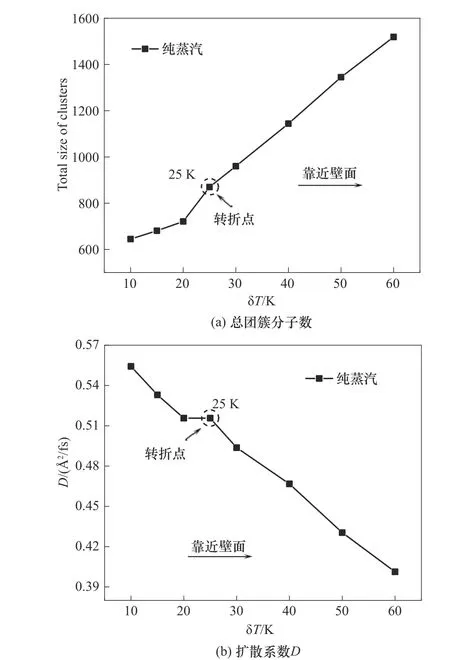
图6 近壁空间中的团簇分布演化的特点Fig.6 Characteristics of clusters distribution evolution in the near wall region

为了进一步探究近壁空间中团簇分布和过冷度的转折点的存在以及变化，模拟了不同体相蒸汽压力下的纯蒸汽冷凝过程，包括初始饱和温度为423 K(0.4760 MPa)，398 K(0.2321 MPa)和373 K(0.1013 MPa)的三个温度对应的不同压力体系，模拟结果如图7 所示，可以看到三个压力条件下均存在特征转折点，当水蒸气的初始饱和温度降低（压力降低）时，转折点对应的δT增大，这说明了团簇尺寸随着离壁距离快速下降，较大的团簇更靠近壁面，团簇分布的稠密区更薄，此外，还发现降低压力对靠近壁面和靠近气相主体区域的团簇的影响相对更大一些，且压力越低，这种影响越突出。

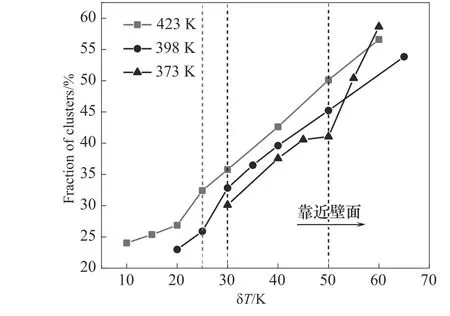
图7 蒸汽压力对近壁空间中的团簇分布的影响Fig.7 Effect of vapor pressure on cluster distribution in the near wall region

3.2 不凝气对近壁空间中团簇分布的影响

由于不凝气的存在对实际的冷凝过程影响非常大，本文进一步探究了相同初始气相温度下含10%氮气的水蒸气体系的冷凝过程。N2分子间作用势使用标准12/6 LJ势，表达式如下：

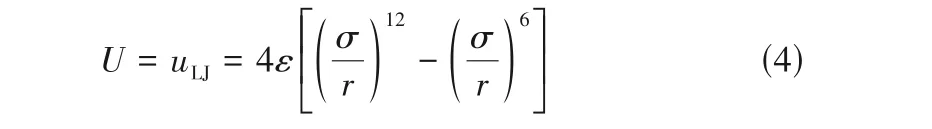
其中，εN-N=0.200527 kcal/mol，σN-N=3.623 Å，根据Lorentz-Berthelot 混合原则[30]有σN-O=(σN-N+σO-O)/2，εN-O=(εN-NεO-O)1/2，计算可得εN-O=0.19271 kcal/mol，σN-O=3.39095 Å。与纯蒸汽的模拟过程类似，首先对整个体系进行能量最小化，紧接着对水分子和氮分子分别进行NVT 系综下的弛豫，控制初始温度为423 K，模拟150 ps,稍微平衡一下，形成一个该温度下正常的随机分布，选用Nose-Hoover 控温方法进行温度控制，最后降低不同的温度δT进行NVT系综下的模拟直到平衡。使用Ovito、Vmd、Origin 和Matlab 软件对输出的结果文件进行数据提取和分析。

与纯蒸汽冷凝类似，在氮气存在的情况下，如图8(a)所示，体系势能随时间不断减小，并最终达到稳定，且δT越大，即距离过冷壁面越近，体系势能下降越快。从MSD 随时间的变化[图8(b)]中同样可以看到δT越大，相应的扩散系数越小。通过统计分析“趋于平衡”的趋势和扩散趋势两趋势的差值，得到对于含10%氮气的冷凝体系选体系中最大团簇都达到60左右的时刻作为比较基准，进一步统计了相应各δT体系中的总团簇分子数以及扩散系数，结果如图8(c)、(d)所示，可以看到对于含10%氮气的水蒸气冷凝，总团簇分子数和扩散系数均在δT=35 K 处出现特征转折点，δT＞35 K 对应稠密分布的近壁区，δT＜35 K为扩散发展过渡区。

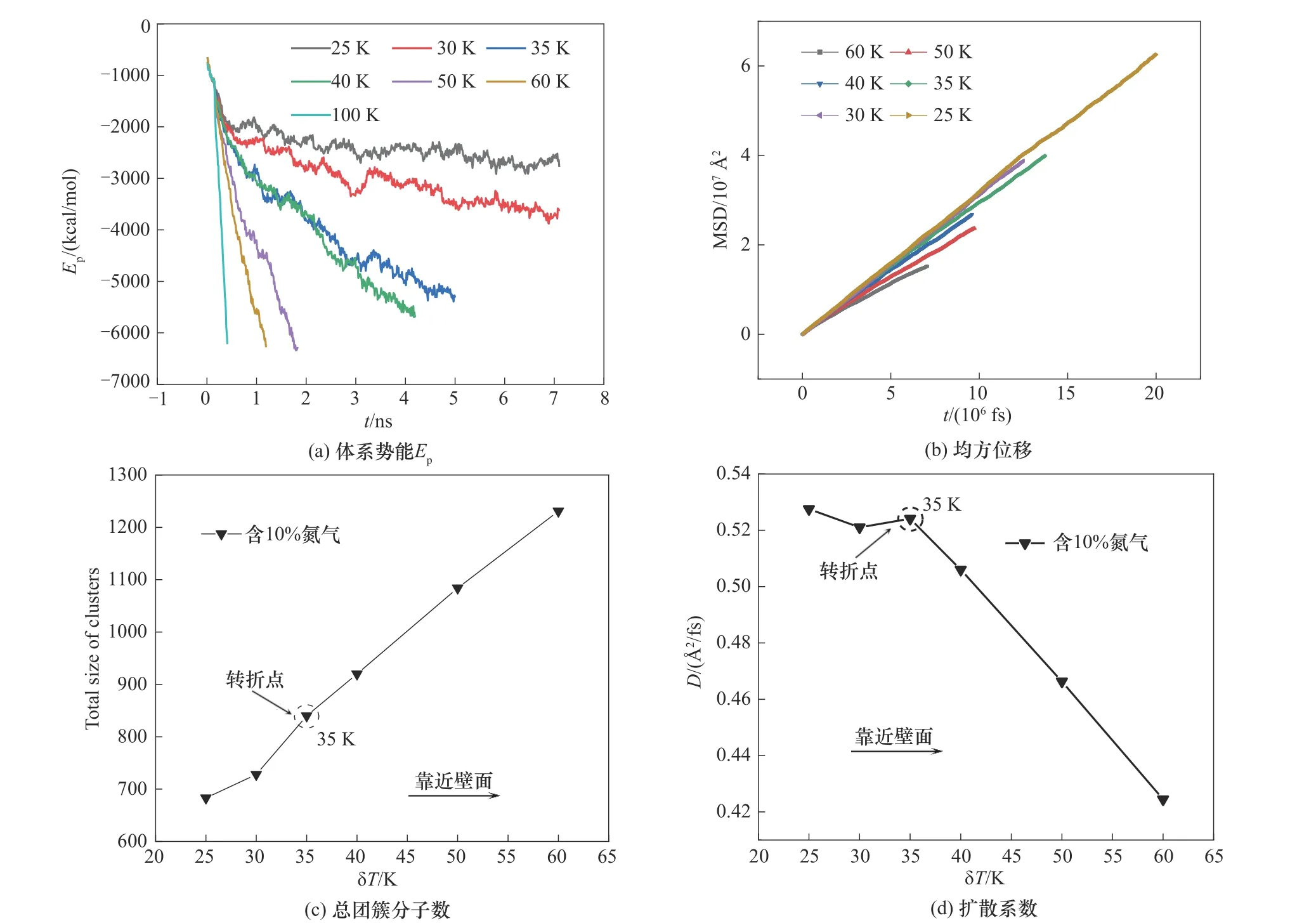
图8 氮气存在下近壁空间中水分子的团聚演化与团簇分布特点Fig.8 Evolution of water molecules aggregation and characteristics of clusters distribution in the near wall region with nitrogen

为了探究不凝气对转折点的影响，在添加10%氮气的基础上，继续增加氮气含量至20%，比较纯蒸汽和不同氮气含量下的团簇的分布演化，结果如图9 所示，发现纯蒸汽冷凝的近壁空间分布的转折点（δT=25 K）小于含10%不凝气（δT=35 K）和含20%不凝气（δT=45 K）冷凝的转折点，并且不凝气含量增加时，转折点δT值增大，说明纯蒸汽冷凝的转折点更靠近气相主体，也就是说纯蒸汽冷凝的团簇分布的稠密区更厚一些，而不凝气的存在使得扩散区变大，所以当体系含不凝气时，要达到与纯蒸汽条件相似厚度的稠密区，需要更高过冷。

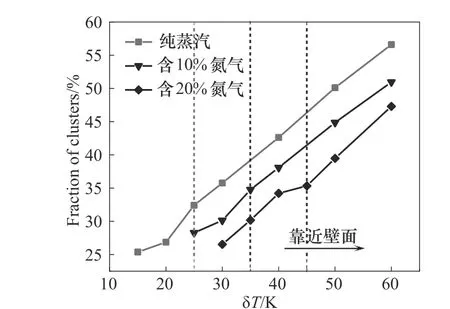
图9 不凝气对近壁空间中的团簇分布的影响Fig.9 Effect of noncondensable gas on cluster distribution in the near wall region

依据本文分析，蒸汽压力或不凝气含量等工艺参数将影响近壁团簇密集区的厚度，以至于最终影响冷凝效果。这个结果从一个新的角度揭示了目前一些冷凝强化效果的微观机理，例如提高过冷度的根本原因在于增加了团簇稠密区的厚度。在冷凝过程的强化结构设计上，也提出了新的设想，即不仅是壁面上的强化结构，强化结构可以拓展到近壁区的空间中去。从这个角度可以借鉴仙人掌刺、沙漠甲虫背部凸起、叶片表面纤毛等生物具有的用于集水的表面化学组成和特征高度结构[31-35]，说明可以通过在空间中加入固相介质来捕获气相团簇；强化结构还可以将团簇尽量控制在稠密区内，减少团簇向外扩散逃逸；甚至还可以通过特定的表面化学成分来限制氮气的运动，从而让水分子获得更大碰撞概率。总之，本文关于近壁团簇分布规律和机理的新发现对实际工程中有冷凝调控需求的表面的设计具有特殊的指导意义。