电场对竖直微槽润湿及毛细流动特性影响

董宜放，于樱迎，胡学功，裴刚

（1 中国科学技术大学热科学和能源工程系，安徽 合肥 230027； 2 中国科学院工程热物理研究所，北京 100190；3 中科南京未来能源系统研究院，江苏 南京 211135； 4 中国科学院大学，北京 100049）

引 言

为提高微槽毛细极限，研究人员采用了优化微槽尺寸[14-17]、表面处理[18-19]等方式以强化微槽内毛细润湿并取得了一定的效果，但增加了加工方式的复杂性和成本。电水动力学效应(electrohydrodynamic,EHD)因功耗小、可靠性强、强化换热效果显著等优势被认为是较为可行的主动强化换热方式[20]。研究发现，电场通过控制液体工质流动[21-22]、电润湿效应[23-32]、提升微槽毛细润湿性能[33-39]等机理可以强化微槽内液体换热。Yu 等[21]通过引入电场驱动微槽热管内工质从冷凝段流动到蒸发段，将微槽热管的最大热输运能力提高到了自然对流的6 倍。Lackowski 等[22]发现电介质液体在非均匀电场作用下受到介电电泳力而倾向于漂移/迁移到高电场强度区域，从而实现电场对微通道内液体流动的控制和驱动。电润湿通过施加电场引起固/液界面润湿性改变，其原理是通过电场将溶液中的电荷吸引到固-液界面，改变固-液界面张力特性，进而引起接触角的变化[23]，从而实现固体表面上的液滴驱动或操纵[24-25]。刘镇等[26]提出了一种以水为工质的电润湿方案，实现了液滴向一侧铺展，并指出场强越大，液滴接触角变化越大，铺展越远；当场强增大到一定值时，液滴出现整体移动趋势。研究人员还对不同润滑液[27]、不同电导率[28]、不同疏水性[29]条件下液滴的电润湿性能进行了研究。Chakraborty 等[30]发现脉动直流场引起液滴的快速振荡导致液滴内部混合，从而增加传热速率。Bahadur 等[31]指出外加电场使传热速率提高了30%，强调了电润湿现象增强传热速率的有效性。Izadi等[32]研究了电润湿驱动下液滴在微槽内的动力学和传热过程，发现在较大的微槽中，流体具有较高的Prandtl 数和平均Nusselt 数。Suman[33]、Saad等[20,34]均发现电场能减缓微槽内液体干涸，进而显著提高微槽热管的毛细极限。Chang等[35]发现平板电极和针状电极两种不同布置形式均强化了微槽热管毛细极限，且平板电极的强化效果好于针状电极。郭磊等[36]发现电场强化了微槽道结构换热表面蒸发/沸腾传热特性，并将其归结于电场对蒸发面的润湿优化和气泡的加速脱离。Yu 等对电场作用下竖直矩形微槽的最大毛细润湿高度进行了理论[37]和实验[38]研究，发现电场可以强化微槽润湿，进而强化微槽换热[39]。

迄今，电场作用下水平或倾斜角度较小的微槽道内的毛细流动、竖直微槽静态润湿特性等的相关研究较为充分，但电场作用下竖直微槽内液体润湿和流动特性的研究较少。因此，本文使用平板电极研究电场作用下竖直微槽内润湿高度、润湿速率随时间的变化情况，同时建立电场作用于微槽内毛细润湿流动的数学模型，探究电场作用下竖直矩形微槽内液体润湿和毛细流动特性，以期通过电场引导微槽内液体毛细流动，改善竖直微槽的毛细极限，对应用竖直微槽热沉的电力电子器件的散热强化提供理论依据。

1 实验系统和方法

1.1 实验测试单元与系统

由微槽群实验件、聚四氟乙烯板(polytetra fluoroethylene，PTFE)等组成的微槽群测试单元如图1 所示。微槽群实验件材质为硼硅玻璃，因具有较低的热膨胀系数和良好的电绝缘性在微槽轴向流动[9，13]和电场作用下微槽内换热特性研究中作为基底材料[37-40]；微槽截面为矩形，如图2 所示，尺寸为宽0.2 mm，深0.7 mm，槽间距0.44 mm。将微槽群实验件固定在PTFE 板上，可起到良好的固定作用。

图1 微槽群测试单元Fig.1 Microgrooves testing unit

图2 微槽群实验件截面图Fig.2 Cross section of microgrooves

采用平板电极为系统施加电场，如图3所示，一对平行板电极布置在微槽群实验件轴向两端，高压电极置于微槽群实验件正下方，与高压电源(B0HER 73030PA，不确定度＜0.1%)正极连接；负极(接地电极)置于微槽群实验件轴向上方并与正极平行，与高压电源负极共地。高压电极为长、宽、厚度分别为20 mm、20 mm、1 mm 的方形铜片，接地电极为宽5 mm、厚0.2 mm 的铜箔。正负平板电极存在蒸汽和液体两种不同介电常数的相态，当施加电场后，正负电极间产生电场，可对微槽群实验件内流体产生定向驱动力。

图3 电场布置情形1—负极(接地电极);2—高压电源;3—微槽群实验件;4—高压电极;5—微槽群固定装置Fig.3 Electric field arrangement

工质为去离子水，是一种电介质，具有稳定性好、无毒、便于制取等优势，在文献[40]中加以使用，其物性由表1给出。使用高速摄像机(Phantom V5.1)拍摄微槽内液体润湿情况，拍摄速度为10 帧/秒，分辨率1024 pixel×1024 pixel。实验在标准大气压下进行，环境温度为24.4℃，湿度为62.6%。

表1 工质物性Table 1 Physical properties

1.2 润湿高度数据处理

1.2.1 润湿高度测量方法 实验过程中，将微槽群热沉实验件洗净后固定，用高速摄像机拍摄无电场情形下微槽群热沉内的液体润湿情形；随后调节高压电源电压值，每次调节后，在高压电极处滴加工质拍摄润湿情况，工质沿微槽轴向润湿流动时会进行二次或多次补液，以保证高压电极处滴加工质的量足够完成润湿过程。PTFE 板上贴有标尺，如图4 所示，对比标尺读出竖直微槽热沉内液体润湿高度，具体过程以4.0 kV、10 s时的微槽润湿高度定格图像为例，使用Origin 绘图软件图像处理模块，将软件的轴线与刻度尺对齐作为基准，将其位置坐标输入到软件中，然后对微槽群热沉中液体的液柱干涸位置进行标记，即可得到微槽群内液体的润湿高度。值得注意的是，由于清洁以及加工误差等各种原因，微槽群实验件内不同微槽道里液体的润湿高度有差异，即润湿均匀度不一，因此在本文中将微槽群实验件各微槽道内液体润湿高度取平均值，即后续提到的“润湿高度”均为轴向平均润湿高度，以图4为例，4.0 kV、10 s时的平均润湿高度为28.64 mm。

图4 润湿高度数据处理Fig.4 Image processing of the wetting height

1.2.2 润湿高度测量误差 使用标尺测量润湿高度，其精度为±0.5 mm，人为操作误差控制在±1 mm，实测润湿高度范围是16～40 mm，所以得到润湿高度测量误差为

2 电场作用对微槽内液体流动特性影响的理论分析

2.1 无电场时微槽内液体流动特性理论分析

对模型进行了必要且合理的假设：(1)沿微槽一维轴向流动；(2)微槽轴向同一截面处曲率相同；(3)蒸汽侧压力恒定；(4)忽略了气液界面处的剪切力，原因是在开放性微槽群热沉中，蒸汽侧空间较大，蒸汽流速较弱；(5)忽略液体蒸发及界面效应；(6)液体的轴向流动为泊肃叶流，动量方程中的惯性力项可忽略[41]。因此，基于力的平衡式，无电场时，竖直矩形微槽内毛细力等于黏性摩擦力与重力之和[1,19]：

2.2 电场作用下微槽内液体流动特性理论分析

在电场作用下，除上述提到的毛细驱动力、黏性摩擦力以及重力外，微槽内液体还会受到电场力的作用，则式(2)可以扩展为电场作用下力的平衡式：

式中，等号右侧第一项为电场施加在自由电荷上的库仑力，qe是流体中的电荷密度，E是电场强度；第二项为介电电泳力，与介电常数的空间变化有关，其中ε为介电常数；第三项为电致伸缩力，和电场随空间位置变化以及介电常数的空间变化有关，当电场均匀时可以忽略[33]，通过计算发现，微槽轴向的电场强度近似均匀[39]，故在此忽略电致伸缩力，这种处理在文献[33-35]中也被采用，故电场体积力可以简化为：

Ce只与电场强度、气液介电常数有关，通过计算发现，微槽轴向的电场强度随润湿高度逐渐下降，但变化程度较小，可假设电场强度近似均匀[39]，故Ce可近似看成常数，则在电场作用下的毛细润湿初期，润湿高度和时间遵循h2-t关系。

在润湿流动后期，库仑力和重力不能忽略，在本文中，重力ρlg的数量级为105N/m3，由文献可知水滴的电荷密度可以达到101.12 nC/μl[43]，在电场强度为103V/m 数量级情况下[39]，可计算得到库仑力的数量级为105N/m3，而介电电泳力数量级仅为10-1N/m3，因此本实验中库仑力对液体流动的影响远远大于介电电泳力，文献[33]也得到了近似结论，基于此，本模型中介电电泳力可以忽略，此时电场作用下力的平衡式(11)可简化为：

3 实验结果与讨论

3.1 电场作用下微槽内液体润湿高度

3.1.1 电场作用下微槽内液体润湿高度随时间变化情况 图5 为电场电压为4.0 kV 时竖直矩形微槽内液体润湿高度随时间的变化情况，此时实验中正负电极间距为47 mm。由图5 可知，在电场作用下，从0 到2.5 s，润湿高度达到了20 mm 左右，是t=20 s时润湿高度34 mm 的59%。可见，在液体浸入微槽的初期，较短时间内润湿高度就达到了较为可观的水平，表明在润湿初期润湿速率较大，而润湿后期液体润湿速率变慢，因此需要较长时间达到最大润湿高度。

图5 4.0 kV时微槽润湿高度随时间的变化Fig.5 Wetting height variation with time under 4.0 kV

图6(a)为有无电场作用下竖直矩形微槽内液体润湿高度h在40 s内的整体变化情况，图6(b)为液体进入微槽初期5 s内，即润湿初期润湿高度随时间的变化。如图所示，微槽内液体润湿高度随时间呈现幂指数增长，液体工质润湿流动初期(0～5 s)，润湿高度急剧增加，且变化最快，也就是润湿速率较大；而润湿流动后期(10～40 s)润湿高度增加缓慢，并趋于平缓，这符合润湿初期h-t1/2和润湿中后期h-t1/3的幂函数增长规律。同时，可以看到，无论是在润湿初期还是中后期，电场均对微槽内液体润湿高度起到了提升作用，这表明电场对微槽内液体流动的影响是连续性的动态过程。

图6 不同电场作用下微槽内润湿高度随时间的变化Fig.6 Wetting height variation with time under different electric field

电场对微槽内液体润湿的原因有两个方面：一方面电场的引入增加了一个驱动液体向上流动润湿的力[式(8)]；另一方面是由于电润湿效应。本文中微槽基底材质为硼硅玻璃，其与工质水的接触角经测量为47°[38]。根据电润湿性原理，电场会影响工质与固体材料之间的接触角，Gao 等[44]发现接触角随着电场的增加而逐渐减小，即润湿性能增强。

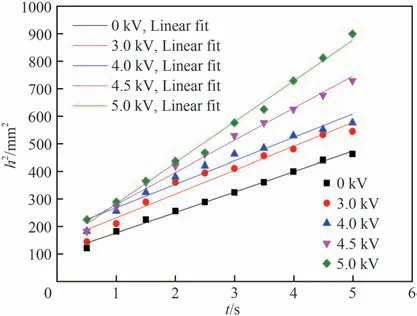
图7 有无电场作用时毛细流动初期h2-t曲线Fig.7 h2-t curve at the beginning of the capillary flow with or without electric field

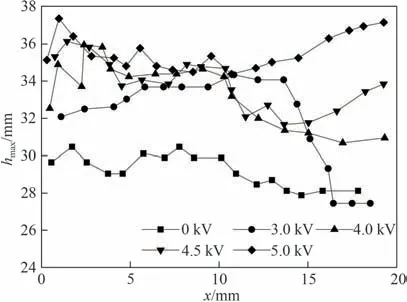
图8 不同电场下微槽最大润湿高度沿x方向分布Fig.8 Distribution of maximum wetting height along with x direction under different electric fields

可见，不同微槽道内因加工尺寸偏差引发电场力沿x方向分布也不均匀，这导致不同电压下最大润湿高度分布有交叉，但整体上来看最大润湿高度随电场电压的增加而逐渐增加，即电场能够提升微槽内液体润湿高度，这是因为电场力与毛细力一样，是驱动液体在微槽道内克服重力和黏性摩擦力向上爬升的力[式(8)]。

图9 不同电场下最大润湿高度强化比对比Fig.9 Comparison of EHD enhanced ratio of maximum wetting height under different electric fields

3.2 电场作用下微槽内液体润湿速率

3.2.1 电场作用下微槽内液体润湿速率变化情况图10(a)、(b)分别为电场作用下微槽内润湿速率随时间和润湿高度的变化情况。如图10(a)所示，在电场作用下，竖直微槽内液体润湿速率在液体进入微槽内的初期最高，然后在5 s 内急剧下降，到20 s 后基本趋于平缓。从图10(b)可以看出，液体润湿速率随润湿高度的增加也呈现逐渐下降趋势。同时，在同一时刻，随着电场电压的增加，润湿高度逐渐增加，润湿速率也逐渐增加，并且在整个流动过程中，电场对毛细润湿速率的影响是持续的。

图10 不同电场作用下微槽内液体润湿速率与时间(a)和润湿高度(b)的关系Fig.10 Wetting velocity variation with time(a)and wetting height(b)under different electric fields

由式(12)和式(14)可知，电场作用下润湿高度随时间分别呈现润湿初期h-t1/2和润湿中后期h-t1/3的关系，则理论上润湿速率也呈现分段效应：

图11 有无电场时微槽润湿初期和中后期v-1/h曲线Fig.11 v-1/h curve for the beginning and long-term period under different electric fields

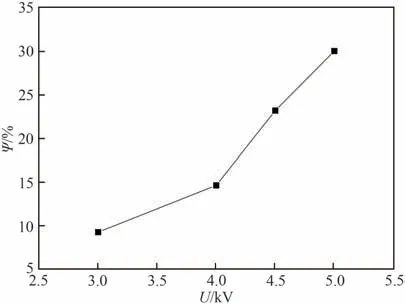
图12 不同电场下平均润湿速率强化比对比Fig.12 Comparison of EHD enhanced ratio of wetting velocity under different electric fields

4 结 论

对电场作用下竖直矩形微槽内液体润湿和毛细流动特性做了实验研究和理论分析，发现微槽内液体润湿高度、润湿速率在电场作用下有如下变化规律。

(1)电场作为一种主动式强化手段，对竖直毛细微槽内液体润湿高度和润湿速率均有强化作用，当电场为5.0 kV 时与无电场时相比，润湿高度强化比可达到30.0%；且电场越强，对润湿高度和润湿速率的强化提升越大。

(2)电场作用下流体在微槽道内的毛细润湿高度随时间的关系呈分段效应：液体在微槽内润湿流动初期，润湿高度的平方与时间呈线性关系，即h-t1/2；润湿流动中后期，润湿高度与时间的1/3 次方呈线性关系，即h-t1/3。这与无电场时毛细流动特性研究结果类似，原因是实验条件下电场强度近似不变，故电场力可近似为常量。(3)电场作用下流体在微槽道内的毛细润湿速率随润湿高度的关系也呈分段效应：在润湿流动初期，润湿速率与润湿高度的倒数呈线性关系，即v-1/h；在润湿流动中后期，润湿速率与润湿高度平方的倒数呈线性关系，即v-1/h2，且润湿速率随时间呈下降趋势。