基于新非线性多重网格法的图像去噪*
2022-08-10杨奋林
韩 粉,杨奋林
(吉首大学数学与统计学院,湖南 吉首 416000)
图像去噪是底层图像处理的重要内容之一.Rudin等设计的全变分(Total Variation,TV)[1]模型可以很好地保护图像边缘,但会使光滑过渡区域产生阶梯效应[2-5].为了避免阶梯效应,学者对TV模型作了改进,构造出在图像边缘正则项为L1范数、在图像平坦区域正则项为L2范数的TVP模型,如基于lp的Directional Total Variation(DTV)模型[3]、分数阶P-Laplace模型[4]、基于Lp伪范数的高阶Overlapping Group Sparsity(OGS)模型[5]等.这些模型均使用梯度模检测边缘,考虑到梯度模不能有效区分图像的边缘和陡峭的斜坡,Chen等[2]使用差分曲率检测边缘,设计了基于差分曲率的TVP模型,并采用最速下降法进行了求解.但最速下降法收敛速度缓慢[6],为了加快基于差分曲率的TVP模型的求解速度,笔者拟设计一种新的非线性多重网格(Nonlinear Multigrid,NM)法,即对差分曲率设置有效的限制算子和插值算子,以期避免网格变化对边缘检测算子灵敏性产生影响.
1 基于差分曲率的TVP模型
图像的差分曲率(D)在图像边缘处大,在图像的平坦、斜坡区域及孤立噪声点处小,它能有效区分图像的边缘和平坦的光滑过渡区域,以及边缘和陡峭的斜坡.基于差分曲率的TVP模型[2]如下:
(1)
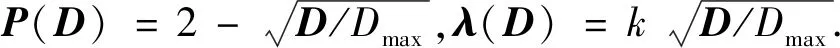
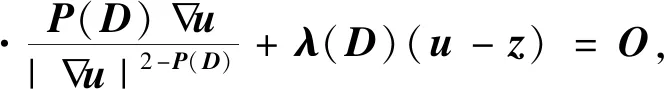
(2)
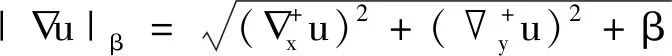
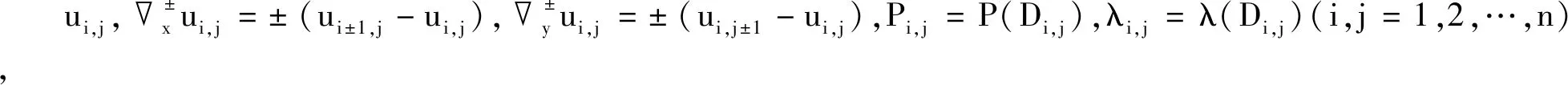
(3)
其中
(4)
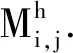
(5)
记非线性方程组(5)及其边界条件为
Nhu=λhz.
(6)
2 新的非线性多重网格法
NM法[6-9]是一种求解椭圆型偏微分方程的快速方法.其基本思想是先在细网格上通过前光滑求出近似解和误差,对误差和残量限制后进入套迭代;在最粗网格上求解残量方程得到误差,接着对误差进行插值,校正近似解并进行后光滑,从而得到最终解.值得注意的是,网格间的转移算子和光滑化方法在很大程度上会影响NM法的性能.
考虑到用NM法求解(6)式时,随着网格的变化,图像的边缘可能会变模糊,差分曲率检测边缘的灵敏性可能会受到影响,笔者将对差分曲率设置合适的限制算子与插值算子,设计出新的NM法.在描述网格间的限制算子和插值算子前,先对最细网格进行标准粗化,即令较细网格上的网格中心点为较粗网格上的节点,得到一系列粗网格上的图像域Ω2h,Ω4h,Ω8h,…,Ω2lh,其中h是网格步长,l≥1是网格重数.
对D进行限制时,令粗网格上每个节点的值等于其对应细网格上邻近9点的加权平均,即
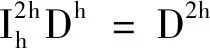
对D进行插值时,若细网格上的节点也是粗网格的节点,则细网格上该点的值等于其对应粗网格上的值;若细网格上的节点在粗网格上的2个节点之间,则该点的值等于其对应粗网格上邻近2点的均值;若细网格上的节点在粗网格上的4个节点之间,则该点的值等于其对应粗网格上邻近4点的均值,即
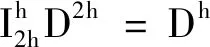
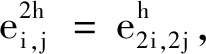
算法1uh←NMG(uh,zh,k,β,v1,v2).
Step1计算输入图像的差分曲率Dh,Ph,λh.若Ωh是最粗网格,则求解(6)式;否则,对uh进行v1次前光滑.
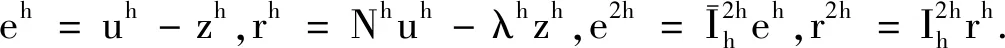
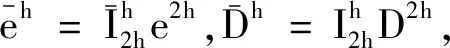
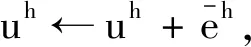
3 实验部分
为了验证新NM法的性能,用该方法和不动点迭代(Fixed Point,FP)法对3幅图像的噪声图进行去噪,并通过峰值信噪比(S)和迭代时间定量分析这2种方法的去噪效果和收敛速度.3幅图像分别是像素为256×256的Lena图、像素为512×512的Fighter图、像素为256×256的Cameraman图,3幅图像的原图及框形区域的放大效果如图1所示.对Lena,Fighter,Cameraman原图依次添加标准差为10,10,20的随机噪声后,图像的峰值信噪比依次为20.983 6,21.761 1,16.524 2.噪声图及框形区域的放大效果如图2所示.利用FP法和新NM法分别对3幅噪声图进行去噪,去噪效果如图3所示.

图1 原图Fig. 1 Original Diagram

图2 噪声图Fig. 2 Noise Diagram


图3 FP法和新NM法的去噪效果Fig. 3 Denoising Effect of FP Method and New NM Method
由图3可见,相比FP法,新NM法去除噪声更干净,去噪后的图像更光滑且没有产生阶梯效应,说明该方法的去噪效果更好.
表1示出了对3幅噪声图分别使用FP法和新NM法去噪后的峰值信噪比和迭代时间.

表1 FP法和新NM法去噪后的峰值信噪比和迭代时间Table 1 Peak Signal-to-Noise Ratio and Iteration Time in FP Method and New NM Method
由表1可知,新NM法的收敛速度是FP法的2~3倍,峰值信噪比比FP法的大0.941 8~1.883 2 dB.
4 结语
构造了一种新的NM法,该方法对差分曲率设置了有效的限制算子和插值算子.相比于FP法,用新NM法求解基于差分曲率的TVP模型,去噪效果更好且收敛速度更快.为了进一步提高峰值信噪比和加快收敛速度,未来考虑从光滑化方法的角度改进NM法,并将改进方法应用于基于差分曲率的TVP模型和高阶模型.
