一类考虑复吸的时滞戒烟模型*
2022-08-10张子振张伟诗
张子振,张伟诗
(安徽财经大学管理科学与工程学院,安徽 蚌埠 233030)
1 问题的提出
生物数学领域学者认为吸烟可以通过社交活动接触传播,因此,近年来他们一直努力基于传染病动力学原理,通过数学建模的方式向人类宣传控烟和戒烟的必要性.尤其是Garsow等[1]提出基本的戒烟模型以后,学者构建了各类戒烟模型,如考虑临时戒烟群体的戒烟模型[2]和考虑偶尔吸烟群体的戒烟模型[3].由于现实世界中多数问题具有一定的不确定性,因此学者进一步构建了具不确定性的戒烟模型,如随机戒烟模型[4]和具有非线性发生率的戒烟模型[5-6].Ullah等[7]在文献[3-4]的基础上,提出了如下考虑复吸的戒烟模型:
(1)
其中:P(t),O(t),S(t),Qt(t)和Qp(t)分别为潜在吸烟者、偶尔吸烟者、重度吸烟者、暂时戒烟者和永久戒烟者在时刻t的数量;Λ,β,μ,α1,α2,γ,δ为模型(1)的参数,Λ为潜在吸烟者的输入率,β为潜在吸烟者和重度吸烟者之间的有效接触率,μ为所有个体的自然死亡率,α1为偶尔吸烟者变为重度吸烟者的比例,α2为暂时戒烟者复吸的比例,γ为重度吸烟者戒烟的比例,δ为永久戒烟者在所有戒烟者中的占比,1-δ为暂时戒烟者在所有戒烟者中的占比.
显然,模型(1)假设偶尔吸烟者变为重度吸烟者是瞬时的,这与现实不相符,因为偶尔吸烟者需要经过一定的时间周期才会对尼古丁产生依赖而变为重度吸烟者.因此,笔者在模型(1)中引入偶尔吸烟者变为重度吸烟者需要经历的时间周期时滞τ:
(2)
2 基本再生数和吸烟平衡点
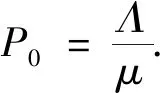
于是
进而有
这里S*是方程
(3)
的正根.这里:
l0=μ((μ+γ)(μ+α1)μ-α1βΛ);
l1=μ(μ+γ)(μ+α1)(α2+β)-α1α2βΛ-α2γμ(1-δ)(μ+α1);
l2=α2β(μ+α1)(μ+γδ).
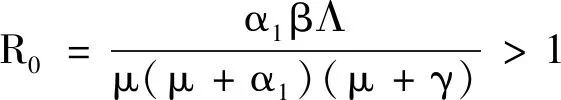
3 局部渐近稳定性和Hopf分岔的存在性
模型(2)在吸烟平衡点E*(P*,O*,S*,Qt*,Qp*)的雅克比矩阵
其中:
m11=-(βS*+μ);m13=-βP*;m21=βS*;m22=-μ;m23=βP*;
n22=-α1;m33=α2Qt*-(μ+γ);m34=α2S*;n32=α1;
m43=γ(1-δ)-α2Qt*;m44=-(α2S*+μ);m53=γδ;m55=-μ.
相应的特征方程为
λ5+Θ4λ4+Θ3λ3+Θ2λ2+Θ1λ+Θ0+(Ξ4λ4+Ξ3λ3+Ξ2λ2+Ξ1λ+Ξ0)e-λτ=0.
(4)
其中:
Θ0=-m11m22m55(m33m44+m34m43);
Θ1=m11m22(m33m44+m33m55+m44m55)+m33m44m55(m11+m22)+
m34m43(m11m22+m11m55+m22m55);
Θ2=-(m34m43(m11+m22+m55)+m11m22(m33+m44+m55))-
((m11+m22)(m33m44+m33m55+m44m55)+m33m44m55);
Θ3=(m11+m22)(m33+m44+m55)+m11m22+m33m44+m33m55+m44m55+m34m43;
Θ4=-(m11+m22+m33+m44+m55);
Ξ0=m11m44m55(m23n32-m33n22)-m55(m13m21m44n32+m11m34m43n22);
Ξ1=m34m43n22(m11+m55)+(m44+m55)(m11m33n22+m13m21n32)+
m44m55n22(m11+m33)-m23n32(m11m44+m11m55+m44m55);
Ξ2=m23n32(m11+m44+m55)-m13m21n32-(m11m33+m34m43)n22-
n22(m44m55+(m11+m33)(m44+m55));
Ξ3=n22(m11+m33+m44+m55)-m23n32;
Ξ4=-n22.
当τ=0时,方程(4)变为
λ5+Λ4λ4+Δ3λ3+Δ2λ2+Δ1λ+Δ0=0.
其中:
Δ0=Θ0+Ξ0;Δ1=Θ1+Ξ1;Δ2=Θ2+Ξ2;Δ3=Θ3+Ξ3;Δ4=Θ4+Ξ4.
根据Hurwitz稳定性判据,当如下方程成立且τ=0时,模型(2)是局部渐近稳定的:
L1=Δ4>0,

当τ>0时,假设λ=iϖ(ϖ>0)是方程(4)的根,那么
(5)
进而得到关于ϖ的代数方程
ϖ10+Κ4ϖ8+Κ3ϖ6+Κ2ϖ4+Κ1ϖ2+Κ0=0.
(6)
其中:
令ϖ2=χ,则方程(6)变为
χ5+Κ4χ4+Κ3χ3+Κ2χ2+Κ1χ+Κ0=0.
(7)
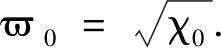
其中
对方程(4)左右两边同时求λ关于τ的导数,得到
于是
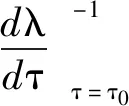
根据文献[10]中关于动力系统产生Hopf分岔的定理,可得如下结果:
定理1如果R0>1,那么当τ∈(0,τ0)时,模型(2)局部渐近稳定;当τ=τ0时,模型(2)在吸烟平衡点E*(P*,O*,S*,Qt*,Qp*)处产生Hopf分岔,并产生一簇分岔周期解.
4 仿真示例
参考文献[7]中的参数取值,同时考虑到模型(2)产生Hopf分岔的充分条件,定义Λ=1,β=0.14,μ=0.001,α1=0.05,α2=0.002 5,γ=0.8,δ=0.48,代入模型(2)可得
(8)
于是R0=1.713 5>1,方程(3)变为
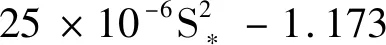
(9)
求解方程(9)得到唯一正根S*=2.173 1,由此可得模型(2)的唯一吸烟平衡点E*(3.276 2,19.543 6,2.173 1,140.532 4,834.470 4),进而得到ϖ0=1.605 6,τ0=25.270 9.当τ=23.379 2∈(0,τ0)时,模型(8)是局部渐近稳定的,此时模型(8)的状态轨迹和相图分别如图1和图2所示;当τ=29.903 9>τ0时,模型(8)失去稳定性,在E*(3.276 2,19.543 6,2.173 1,140.532 4,834.470 4)附近产生Hopf分岔和一簇分岔周期解,此时模型(8)的状态轨迹和相图分别如图3和图4所示.
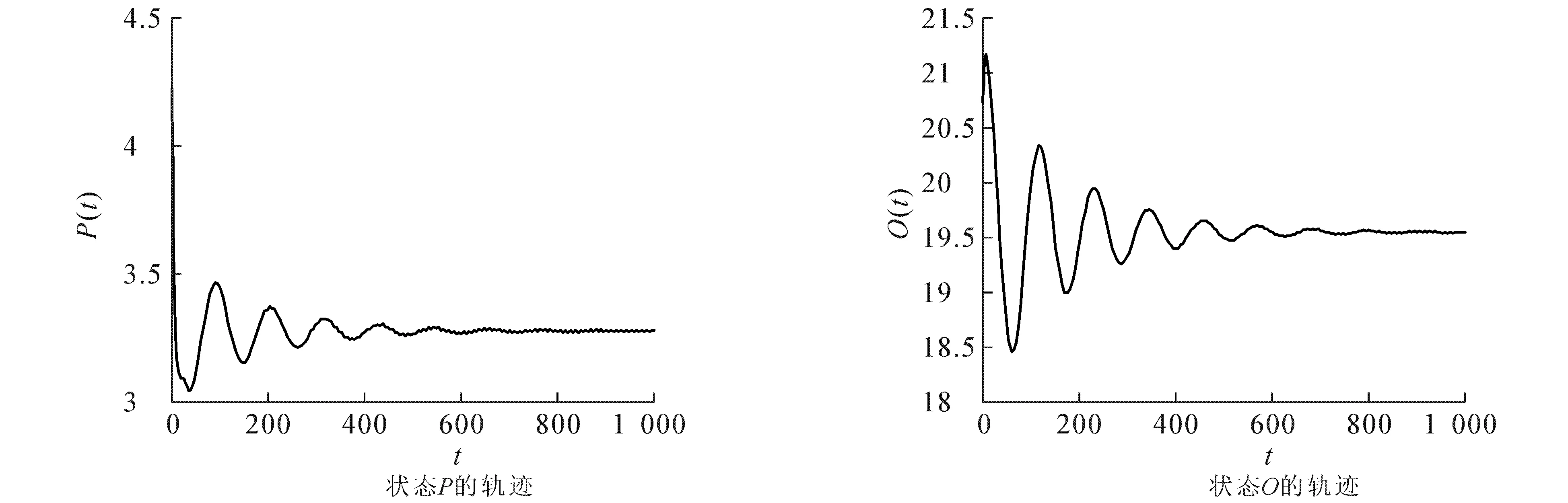
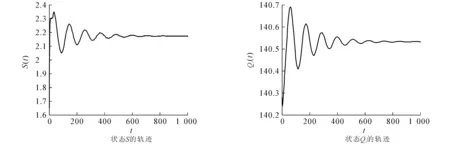
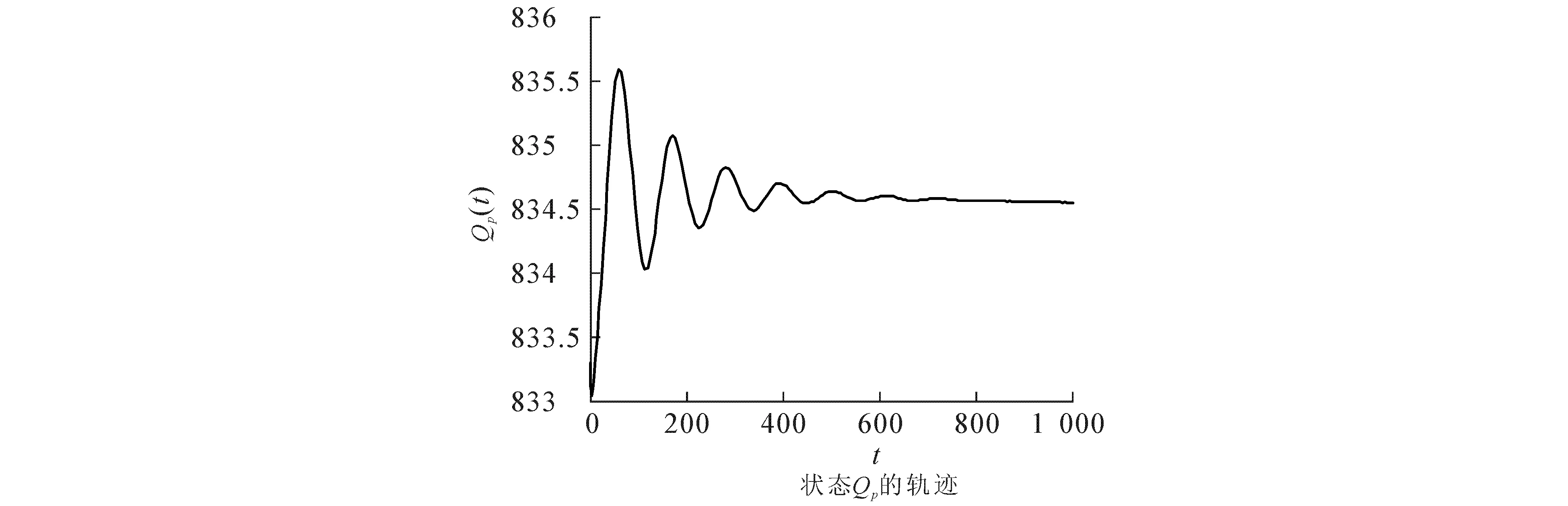
图1 当τ=23.379 2时,模型(8)的状态轨迹Fig. 1 State Trajectories of Model (8) When τ=23.379 2
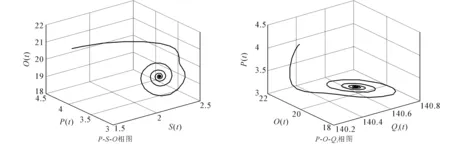
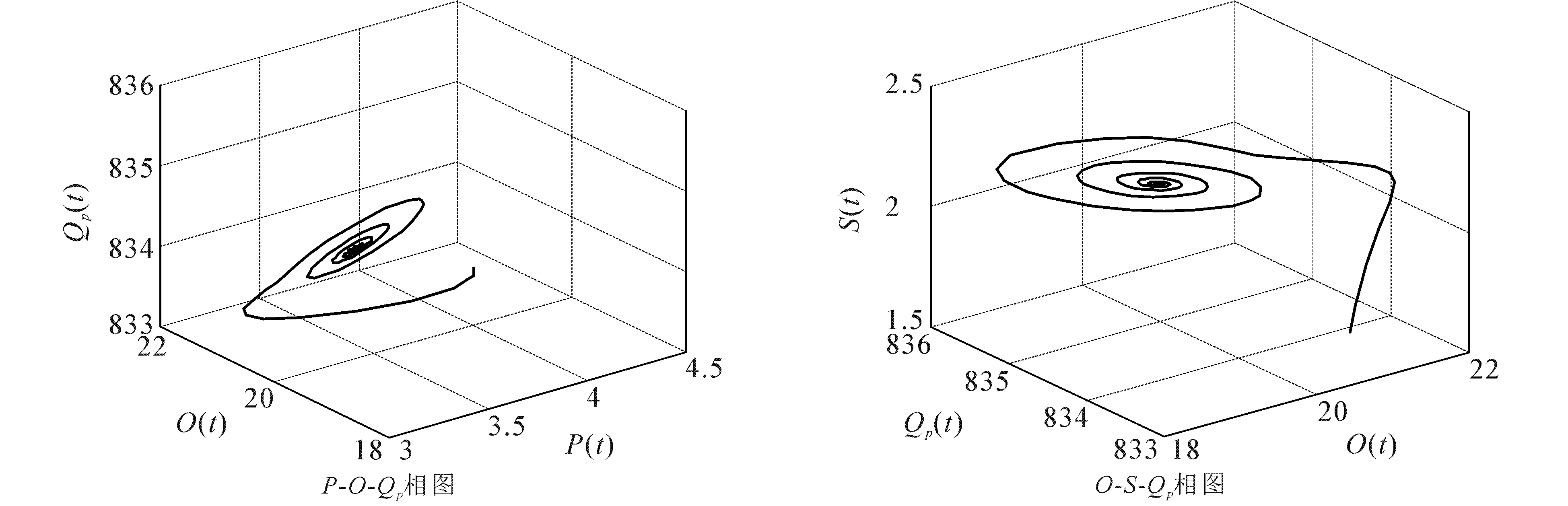
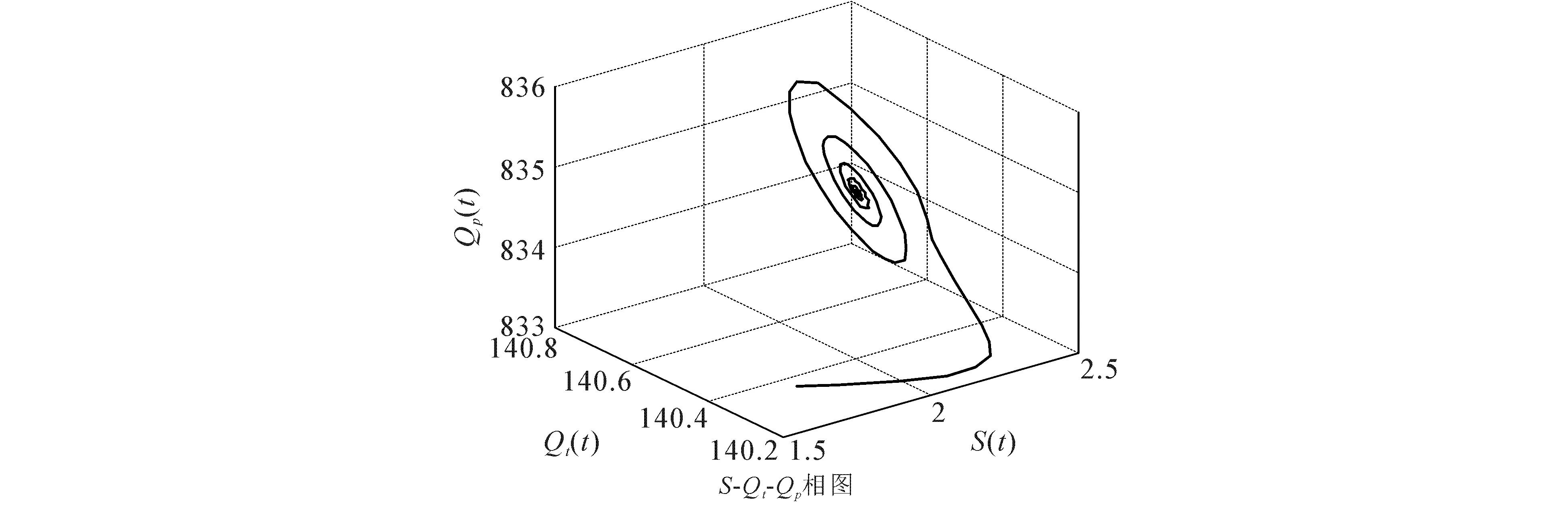
图2 当τ=23.379 2时,模型(8)的相图Fig. 2 Phase Plots of Model (8) When τ=23.379 2
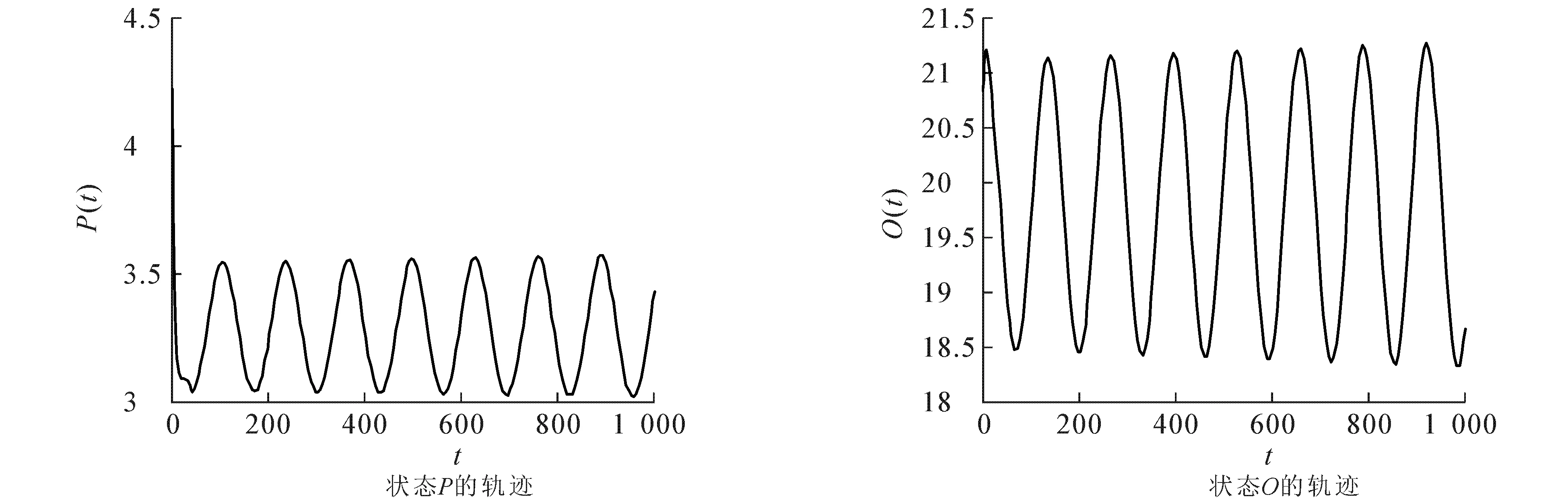

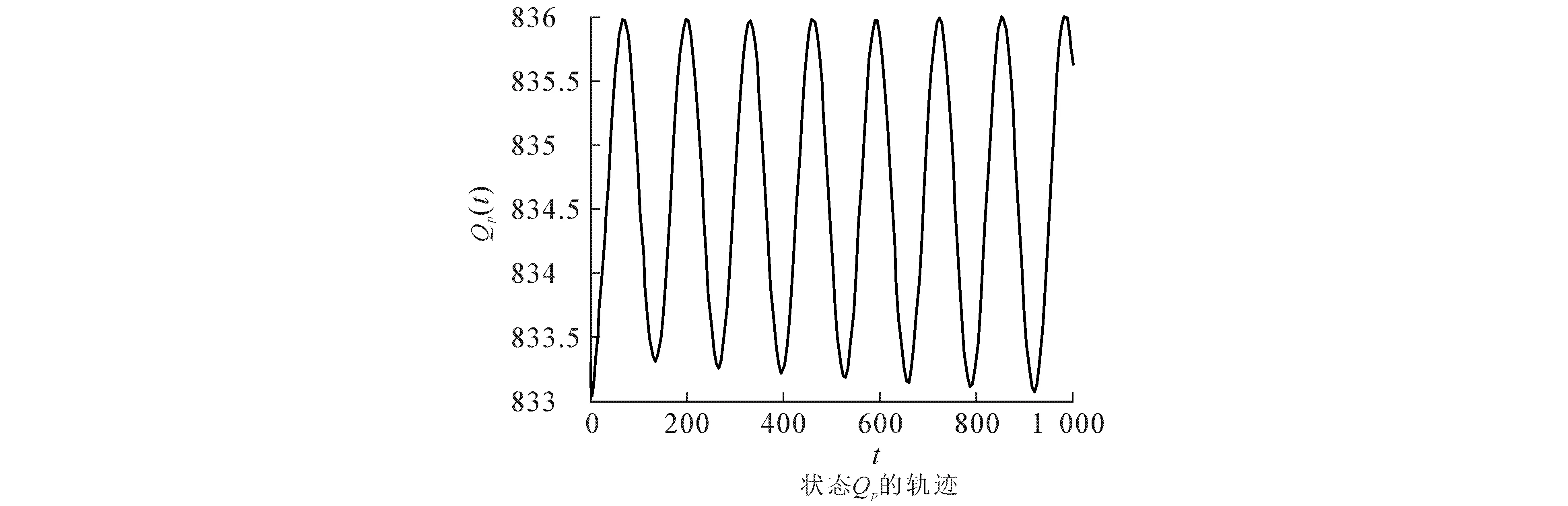
图3 当τ=29.903 9时,模型(8)的状态轨迹Fig. 3 State Trajectories of Model (8) When τ=29.903 9
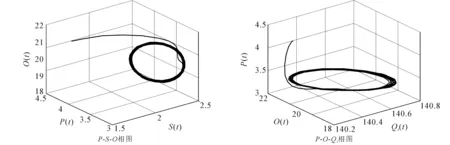
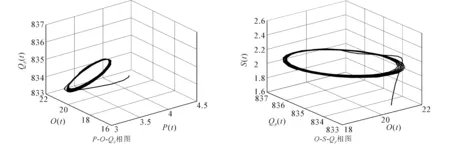
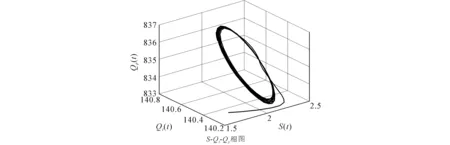
图4 当τ=29.903 9时,模型(8)的相图Fig. 4 Phase Plots of Model (8) When τ=29.903 9
5 结语
在文献[7]的基础上引入偶尔吸烟者变为重度吸烟者需要经历的时间周期时滞,研究了一类考虑复吸的时滞戒烟模型.首先计算出模型的基本再生数和吸烟平衡点,然后以偶尔吸烟者变为重度吸烟者需要经历的时间周期时滞为分岔参数,推导出模型的局部渐近稳定和产生Hopf分岔的充分条件,进而计算出模型产生Hopf分岔时滞的临界点.研究结果表明,时滞取值足够小时,模型处于理想的稳定状态,此时有利于控制吸烟的流行传播;时滞取值越过临界点τ0时,模型失去稳定,产生Hopf分岔,此时不利于控制吸烟的流行传播.值得注意的是,笔者只研究了模型(2)的局部稳定性和Hopf分岔的存在性,并未对Hopf分岔的方向及稳定性等展开讨论.下一步,笔者将深入研究Hopf分岔的性质.
