基于改进栈式降噪自编码器的控制系统故障诊断
2022-08-10赵聪杰武博翔
罗 毅 赵聪杰 武博翔
(华北电力大学控制与计算机工程学院 北京 102206)
0 引 言
随着自动化技术水平及计算机技术不断进步,现在工业系统规模逐步趋向于大型化和复杂化,结构越来越复杂。控制系统中的结构相互关联耦合,单一部件发生故障时,往往引起连锁反应,造成重大安全事故[1]。在当前工业系统中,控制系统主要由控制器、执行器、被控对象和传感器等组成。随着智能化程度的提高,控制器和被控对象设备的稳定性和可靠性有了显著的提高,传感器故障和执行器故障成为控制系统中主要故障,占系统故障的80%左右。传感器和执行器故障主要为恒增益故障、恒偏差故障、慢漂移故障和卡死等。传感器和执行器作为控制系统中基本设备,其分布面广,数量多,且其故障具有随机性和隐蔽性[2]。目前针对控制系统的故障诊断手段主要还是巡检等方法,浪费大量的人力和物力,难以及时有效地发现故障并修复故障。因此,建立快速高效的故障诊断系统及时发现故障、处理故障,对保障系统安全可靠的运行具有重要的意义。
目前,故障诊断方法主要为基于知识的方法、基于解析模型的方法和基于数据驱动的方法[3-4]。现阶段,人工智能技术在工业过程中大力发展,现场总线控制系统和分布式控制系统在工业控制系统中得到广泛应用。支持向量机(SVM)[5]、BP神经网络[6]等基于数据驱动的机器学习算法在故障诊断领域得到大量的应用。1986年,Rumelhar等[7]首次提出自动编码器(Auto-Encoder,AE)的概念,并将其用于处理高维复杂数据。Hinton等[8]在2006年提出了非监督逐层贪婪训练的算法,使得栈式自编码器成为可能。栈式自编码器在无监督学习中具有巨大优势,从较少的无标签数据中,通过自学习提取故障特征,使模型具有强大的表达能力和鲁棒性,广泛地应用于回归、分类领域。曲星宇等[9]提出Dropout降噪自编码器来解决数据线性不可分和高复杂度的问题,将该方法应用于磨矿系统故障诊断中,具有较高的分类准确率。洪骥宇等[10]将降噪自编码器与萤火虫径向网络相结合对航空发动机气路故障进行诊断,通过实例验证了算法的优势。陈仁祥等[11]建立栈式稀疏加噪自编码器进行滚动轴承损伤程度诊断。孙文珺等[12]提出稀疏自编码器深度神经网络实现感应的故障诊断。另外,栈式自编码器在图像识别[13]和情感识别[14]等领域也得到广泛的应用。
本文提出一种基于KPCA-SDAE神经网络模型的控制系统故障诊断方法。利用KPCA良好非线性数据处理能力和栈式降噪自编码器强大的故障特征提取能力,实现了控制系统中故障数据特征的有效提取,并通过Softmax分类器实现故障的分类,从而构建了完整的KPCA-SDAE神经网络故障诊断模型。KPCA-SDAE神经网络模型,通过较少的故障数据便能够实现故障数据的深度挖掘,对于控制系统中故障数据少和特征不明显的情况具有明显的优势,极大地提高了控制系统中慢漂移故障诊断的准确率。并通过人为对数据加入噪声,使网络模型对输入信号具有更强的鲁棒性。最后通过TE控制系统仿真实验验证了该算法的有效性。
1 KPCA-SDAE的基本原理
1.1 核主成分分析基本原理
核主成分分析是对主成分分析(Principal Component Analysis,PCA)的非线性扩展,PCA是线性的,但工业控制系统中的数据大多数为非线性数据,其对于非线性的数据往往显得无能为力。KPCA通过核映射的方法,运用非线性函数将数据映射到高维特征空间,再在特征空间中对数据进行线性操作,深度挖掘数据的非线性信息,提取更多特征[15]。
通过非线性映射函数φ(·)将原空间数据X=(x1,x2,…,xm)映射到高维空间得到特征样本数据Φ(X)=(φ(x1),φ(x2),…,φ(xm)),通过式(1)求得特征向量W=(w1,w2,…,wd):
Φ(X)Φ(X)TW=λW
(1)
式中:λ为特征向量W的特征值。
由式(1)得到式(2):
(2)
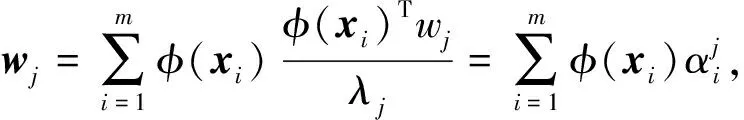
将式(2)代入到式(1)并左乘Φ(X)T得到:
Φ(X)TΦ(X)Φ(X)TΦ(X)A=λΦ(X)TΦ(X)A
(3)
令核矩阵K=Φ(X)TΦ(X)得到式(4):
KA=λA
(4)
通过式(4)求取高维空间下的特征值,将求得的特征值进行排序,得到:λ1≥λ2≥…≥λd,取K中最大的d个特征值对应的特征向量,得到核主成分分析后的降维数据,完成特征提取。
1.2 自编码器的基本原理
自编码器是一种无监督学习算法,多用于高维数据处理。自编码器分为两个部分:编码器和解码器[7]。单层自编码器是一种对称的三层网络结构,如图1所示。

图1 自编码器网络结构
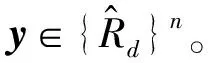
编码过程可表示为:
h=f(x)=Sf(Wx+b)
(5)
式中:Sf为编码器的激活函数;编码器的参数为θ={W,b},其中W为编码器权重矩阵,b为编码器偏置矩阵。
解码过程可表示为:
y=g(x)=Sg(W′x+b′)
(6)
式中:Sg为解码器的激活函数;解码器的参数为θ′={W′,b′},其中W′为解码器权重矩阵,b′为解码器偏置矩阵。
自编码器通过训练数据,不断修正重构误差,使得误差最小化,从而得到最优网络参数θ和θ′。重构误差函数表达式为:
J(W,b)=minL(x,y)=minL(s,g(f(x)))
(7)
式中:L(·)表示为损失函数。根据不同数据的形式,损失函数可用平方误差函数或者交叉熵损失函数,分别如式(8)和式(9)所示,本文模型选用交叉熵损失函数。
(8)

(9)
通过训练得到隐藏层编码矢量h,再经过解码得到重构数据y。如果损失函数与原始输入x误差较小,则认为经过自编码器训练,对数据实现了重构,学习到复现原始数据的能力,完成故障特征提取。
1.3 降噪自编码器的基本原理
降噪自编码器(Denoising Auto-Encoder,DAE)[16]通过在输入样本数据中添加噪声,使样本部分被破坏,将经过处理的数据作为自编码器训练数据,使输出数据尽可能地复现原始数据。DAE经过编码器和解码器的学习重构,使模型获得的数据特征更具鲁棒性,降低对微小扰动的敏感。降噪自编码器的基本原理如图2所示。

图2 降噪自编码器
2 KPCA-SDAE神经网络
2.1 SDAE神经网络结构
SDAE神经网络将前一层DAE的输出作为下一个DAE的输入,经过多层DAE的数据特征提取,能够有效地挖掘出故障数据之间的关系,使得SDAE具有更加强大的表达能力[11-12]。多层DAE网络为无监督学习,通过层层特征提取只能输出为原始数据的重构,为使SDAE具有分类识别的功能,在SDAE最后输出层加入Softmax分类器。Softmax分类器通过计算给出每个类别的概率,能够实现多个故障分类,在多分类问题上具有广泛的优势[17]。经SDAE提取的特征,作为Softmax的输入,输出为故障的类型,其中输出层中神经元的个数为故障种类数。SDAE神经网络结构如图3所示。

图3 SDAE网络结构
2.2 KPCA-SDAE算法实现
本文将KPCA与SDAE相结合,KPCA将故障数据映射到高维空间,对其进行主导成分特征提取,经处理后的数据,故障特征更加明显,输入到SDAE神经网络模型中。SDAE神经网络模型经过无监督训练获得隐藏层网络参数,实现故障特征的检测,并与Softmax级联作为整体网络模型进行有监督训练,实现系统故障的分类。将KPCA与SDAE相结合,通过KPCA高维映射处理和SDAE神经网络模型的网络训练两次数据分析处理,能够有效地提取控制系统非线性故障数据特征,极大地提高了模型对慢漂移故障数据变化的检测识别能力和故障诊断精度。
针对控制系统故障特性,构建4层神经网络。其中第1层为SDAE的输入层;第2层和第3层为隐藏层,通过无监督方式对数据逐层预训练,获得初始权重和偏置;第4层为分类层,通过带标签数据对整个神经网络进行有监督的微调,提升SDAE的性能表现。其算法实现流程如图4所示。
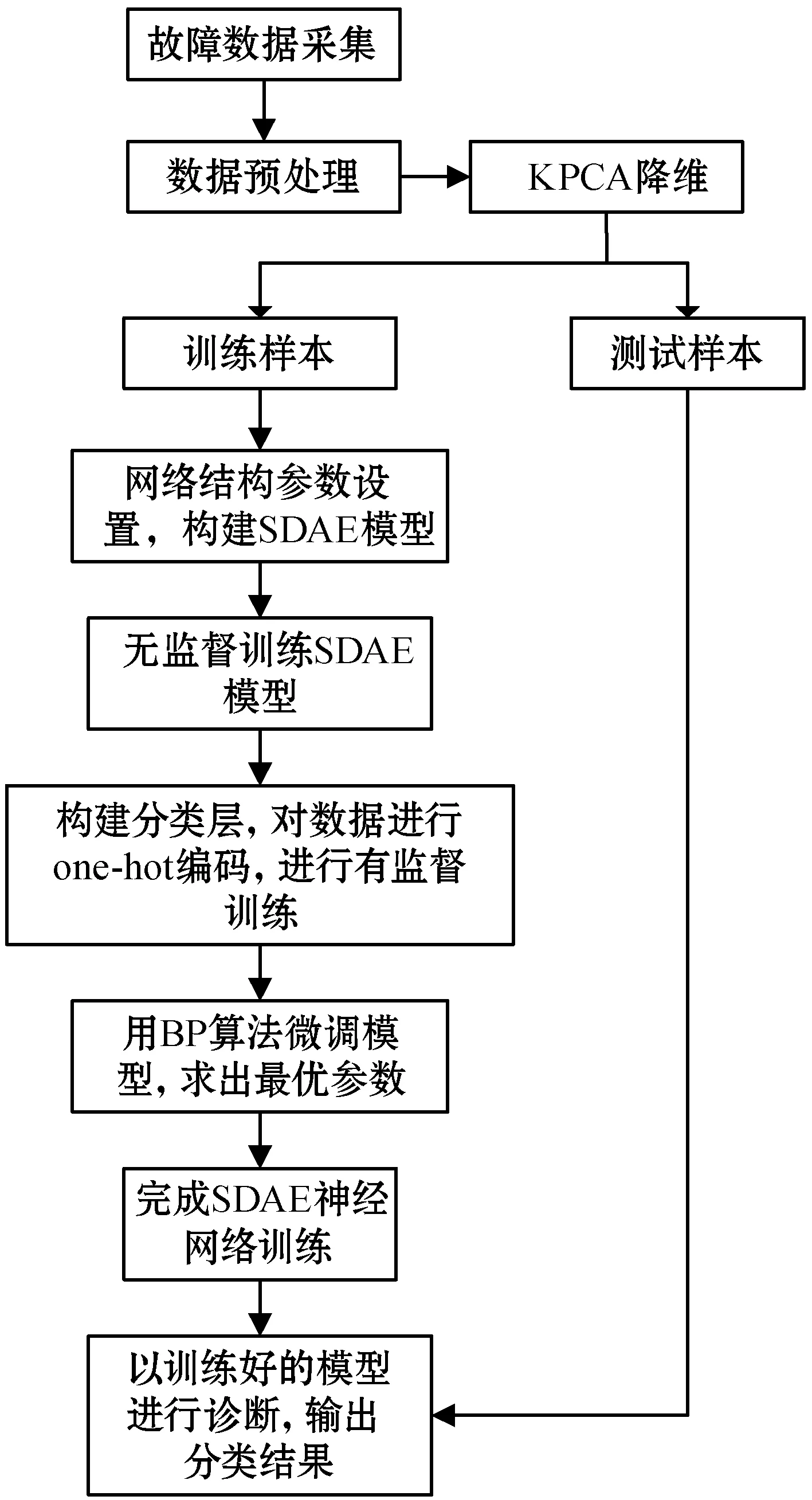
图4 KPCA-SDAE算法流程
该算法流程主要包括:
(1) 故障数据采集并对数据进行标准化和归一化预处理,将其值归一化到[-1,1]范围内。
(2) 将预处理后的数据进行KPCA处理,将非线性数据映射到高维空间进行主元分析,提取主导成分,实现数据的降维。将数据分为训练数据和测试数据,作为SDAE的输入数据。
(3) 设置神经元个数、加噪比例,初始化网络结构,进行无监督训练,每一层的输出作为下一层的输入,利用批量训练法随机选取批量数据进行迭代运算,获取最优权值W和偏置b。
(4) 以Softmax分类层作为输出层,根据故障个数确定输出神经元个数,对数据进行one-hot编码,通过有标签数据进行有监督训练,最后用BP算法对网络参数进行微调优化。
(5) 将测试样本输入到训练好的SDAE中,输出故障类型,实现对控制系统的故障诊断。
3 实验与结果分析
3.1 实验数据来源
本文选取TE(Tennessee Eastman)控制系统[18]模型为实验仿真模型,对控制系统进行故障诊断研究。TE过程是美国Eastman化学公司依据一个实际化工控制系统开发的化工模型仿真平台,TE过程产生的数据具有强耦合、非线性的特征,能够有效地测试控制系统故障诊断模型。
TE控制系统中共有53个变量,操作变量为12个,过程测量变量为41个。在41个测量变量中,过程变量为22个,成分变量为19个。TE仿真控制系统中共预设有21种不同的故障,其中故障1-7为阶跃故障,故障8-12为随机故障,故障13为慢漂移故障,故障14-15为控制阀粘住故障,故障16-21为未知故障[19]。每一种故障包含测试数据960组和训练数据480组。测试数据仿真时间为25 h,每3 min采集一次数据,故障发生在系统运行1 h后;训练数据仿真时间为48 h,故障发生在8 h后。
3.2 实验参数设置
本文选取故障1、故障4、故障6、故障10、故障13和故障14共6个故障进行实验研究。以上6种故障的具体描述见表1所示。
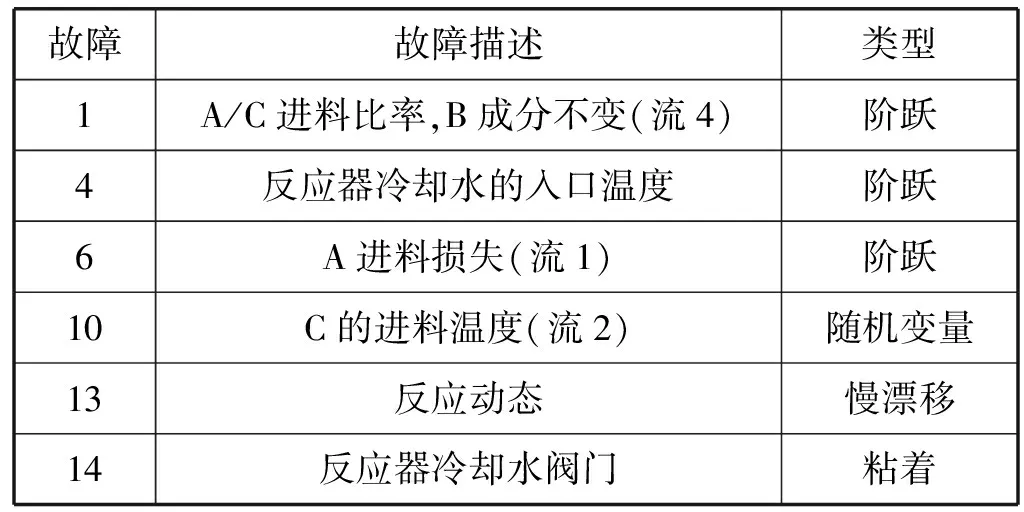
表1 TE过程故障描述
针对这6种故障,每个故障选取480个训练数据,200个测试数据。SDAE神经网络模型学习率设置为0.01,加噪比例设置为0.3,输出神经元为6,批量数据设置为128,每层训练迭代次数为500次。
激活函数选择tanh函数,其运算简单、收敛速度快,在神经网络中具有很好的拟合效果,其数学形式为:
(10)
损失函数选取交叉熵函数,交叉熵函数刻画的是真实概率与预测概率之间的距离,在分类问题上具有广泛的优势。
优化器选取自适应学习率优化器Adam算法,Adam算法依据训练次数而自动改变学习率,在实验中能够快速地实现梯度下降。
数据的标签选用one-hot编码为数据标签。本文共有6个故障,所以设置向量[1 0 0 0 0 0]表示故障1,向量[0 1 0 0 0 0]表示故障2,以此类推表示系统的故障。
首先对6个故障数据进行KPCA分析处理,提取故障数据的主导成分,故障数据维数降为37,经过处理的后的数据添加0.3倍高斯噪声作为SDAE网络模型的输入。SDAE神经网络模型每个隐藏层以重构输入数据为目标进行无监督学习,获得最优权值W和偏置b,完成故障特征提取。最后将第2层隐藏层输出数据作为Softmax分类器的输入数据,利用标签数据进行有监督训练。并通过BP神经网络对整个神经网络模型进行微调优化,完成模型训练,最后利用测试数据对训练好的KPCA-SDAE模型进行故障测试。
3.3 结果与分析
为检验故障诊断结果,选取BP神经网络和RBF神经网络、SDAE神经网络与KPCA-SDAE神经网络作对比。RBF神经网络分类结果如图5所示。
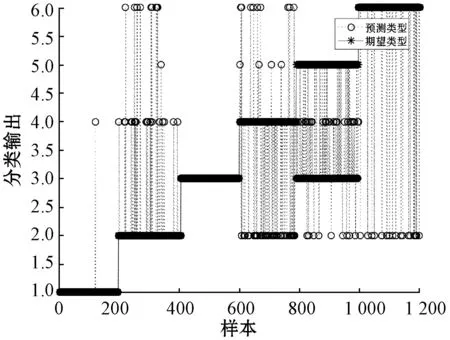
(a) RBF神经网络分类输出
BP神经网络分类结果如图6所示。

(a) BP神经网络分类输出
SDAE神经网络分类结果如图7所示。
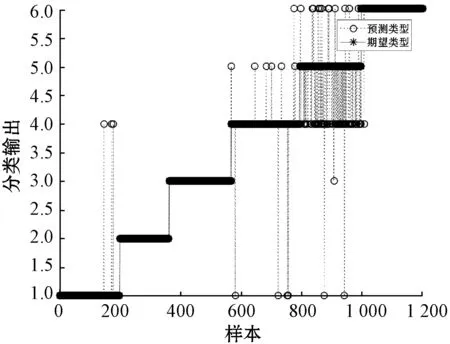
(a) SDAE神经网络分类输出
KPCA-SDAE神经网络分类结果如图8所示。

(a) KPCA-SDAE神经网络分类输出
通过四种神经网络分类结果图形对比,可以看出四种方法都能够准确分类故障1,对于故障4、故障10、故障14,RBF神经网络分类能力较弱。对于故障6,BP有较明显的错分情况,准确率较低。错误故障分类多集中在故障13上。对于故障分类误差,RBF的分类误差较大,多分布在两类误差之上;BP相对较小,差距在一类误差之间居多,SDAE的分类误差明显较小且多分布于一类误差之间,KPCA-SDAE分类误差个数较少,相对比较分散,相较于SDAE神经网络、BP神经网络和RBF神经网络具有一定的优势。故本文方法在控制系统故障分类中要优于其他三种方法。为更进一步地将KPCA-SDAE方法与另外三种神经网络模型进行比较,将三种方法的各故障分类准确率进行分析,如表2所示。

表2 故障分类准确率结果(%)
可以看出,对于故障1,四种算法基本都能准确分类,准确率都在95%以上。对于故障4、故障10、故障14三种故障,RBF神经网络故障诊断准确率较低,SDAE故障诊断效果较好,准确率最高,BP神经网络故障诊断准确率高于RBF神经网络,KPCA-SDAE模型准确率虽然不是最高,但依旧维持在一个较高的水平,能够准确地识别故障类型。而对故障6的诊断中BP神经网络准确率要低于RBF神经网络,RBF神经网络、SDAE和KPCA-SDAE均达到了100%的准确率,BP神经网络只有87.68%。针对故障13,三种算法准确率都比较低。故障13为慢漂移故障,特征不明显,SDAE神经网络模型难以完成其故障诊断,故障特征较为隐蔽。KPCA通过将故障数据映射到高维空间,在高维空间对其进行线性变换,有效地提取出故障13种故障特征,将处理后的数据输入到SDAE神经网络模型中,识别出其微小特征,解决了故障特征不明显导致故障诊断错误的问题。
综合分析,KPCA-SDAE神经网络故障诊断准确率优于BP神经网络、RBF神经网络和SDAE神经网络,尤其在控制系统慢漂移故障诊断中,其准确率要远高于其他三种故障诊断方法。因此,本文提出的KPCA-SDAE神经网络模型在控制系统中具有更强故障诊断能力和故障诊断精度。
4 结 语
本文提出的KPCA-SDAE模型在控制系统故障诊断中具有较好的性能并通过实验验证了该方法的有效性。KPCA具有强大的非线性非高斯数据处理能力,能够深度挖掘非线性数据的信息,降低数据的维数。经过 KPCA处理的数据故障特征更加明显,训练速度更快。SDAE神经网络方法通过数据降噪能力的学习,使得训练模型能有效地降低噪声数据的干扰,增强模型鲁棒性。通过实验结果证明在控制系统故障诊断中KPCA-SDAE神经网络故障诊断效果最优,虽然SDAE神经网络方法具有降维的功能,但是其在故障诊断效果并不好,尤其对于慢漂移故障诊断精度相较于SDAE模型有了显著提高,解决了控制系统中慢漂移故障诊断效果差的问题,验证了该模型的可行性和优势。但是KPCA-SDAE神经网络模型针对的只是已经发生过此类故障的诊断,对于新故障,难以及时有效地进行监测和诊断。如何使模型实现自我更新,提高网络自适应能力,实现故障的识别与分类,需要进行更深入研究。
