基于支持向量机模型的机场行李码放策略

洪振宇 张 聪

(中国民航大学 天津 300300)

0 引 言

目前全球机场旅客运输量超过7千万的机场达到11家，其中，亚特兰大国际机场和北京首都机场的旅客运输量已经超过1亿，平均每天运送行李超过20万件，并且从近几年的变化趋势来看，旅客运输量仍在持续增长，这对机场的高效、安全运营提出了挑战。旅客行李转运效率是衡量机场运行保障能力的关键指标。机场离港旅客行李转运过程包括两个阶段，第一阶段是在航站楼内从旅客值机到行李分拣口；第二阶段是在飞行区将行李从分拣口运送至预定航班上。目前，行李处理的第一阶段由自动化的行李处理系统完成，该系统技术比较成熟，已经实现了危险行李自动识别与分拣。而在行李转运过程的第二阶段，完全依靠人工，这也成为行李转运效率和安全的瓶颈。采用机械手代替人工搬运行李是提高机场行李转运效率的有效方法，而机械手的码放策略又直接影响机场行李的转运效率，所以对机械手的码放策略的研究是非常必要的。

机场行李转运要求机械手在无法提前预知行李尺寸的情况下，较短时间内根据行李车内布局给出行李的码放位置，并使行李车得到较高的空间利用率。因此机场行李转运问题不仅是三维装箱问题，而且还是一个复杂的在线决策问题。三维装箱问题按照货物的尺寸不同分为单构型装箱问题和异构型装箱问题，按照使用容器的不同分为单箱装箱和多箱装箱问题，对于异构型货物的装箱问题在数学上属于NP-hard[1]问题，很难得到精确解，目前对于NP-hard问题大多数学者采用的是启发式算法，George等[2]提出采用基于“层”或“墙”的构造性启发算法；Bischoff[3]在George的基础上提出了基于“完全层”的启发式算法，将二维装箱问题应用到三维空间；Fanslau等[4]进一步扩展了“块”的概念，提出复合块的思想，设计了一种有效的启发式算法；张德富等[5-6]提出一种混合模拟退火算法,随后又提出了三维装箱问题的组合启发式算法；刘胜等[7]提出求解三维装箱问题的启发式正交二叉树搜索算法,该算法装箱效率已有显著提高，但当箱子种类较少时，效果就会不理想。除此之外其他一些学者也取得了较好的研究成果[8-12]。

虽然启发式算法在解决三维装箱问题取得了显著成果，却不能解决码放过程中的在线决策问题，为了解决这一问题我们引入支持向量机模型(Support Vector Machine，SVM)，支持向量机是机器学习[14]重要算法之一，由Cortes等[13]于1995年提出，在解决样本数量少、非线性及高维度的分类问题[14-15]时表现出许多特有的优势，将稀疏化理论[16]与最小二乘支持向量机模型(Least Squares Support Vector Machine， LSSVM)结合的多层训练网络近年来也得到了广泛应用[17]。

为了同时解决机场行李转运过程中存在的NP-hard问题和在线码放问题，本文提出基于空间离散算法的机场行李码放策略，通过行李车与行李空间离散化，将行李车连续空间的无数个可码放位置转化为空间单元节点个数种有限个可码放位置，使系统的运算速度更快、效率更高。同时使用深度稀疏最小二乘支持向量机模型训练，学习工人的码放经验，使算法在最短的时间内计算出行李最佳码放位置，并且在码放结束时可以得到接近人工码放的空间利用率，满足机场的需求。

1 码放策略

在机场行李运输的过程中，行李由分拣系统传送带依次有序运送至分拣口，由机械手完成码放，行李按照先来先放的顺序进行码放，尽可能地实现使用行李车数量最少并且每个行李车的空间利用率达到最高，因此当一个行李进入码放区域时需要机械手在较短时间内给出合理的码放策略，决定行李码放位置，而且机场行李尺寸大小不一，无法提前获得，需要一个有效的评价方案用来评价该位置的优劣，为了便于对码放位置的评价，将行李车和行李空间离散化。

1.1 评价方法

公设行李车的长、宽、高分别为L、W、H；行李的长、宽、高分别为lj、wj、hj，(j表示第j种类型的行李)，采用笛卡尔坐标系将行李车的左下角设为坐标原点，行李车的长度方向为x轴，宽度方向为y轴，高度方向为z轴，本文提出的空间离散算法的概念，将机场行李车和行李离散为由各单元组成的计算模型，离散后的单元与单元之间采用单元节点连接如图1和图2所示，单元节点可以记录空间的状态信息。

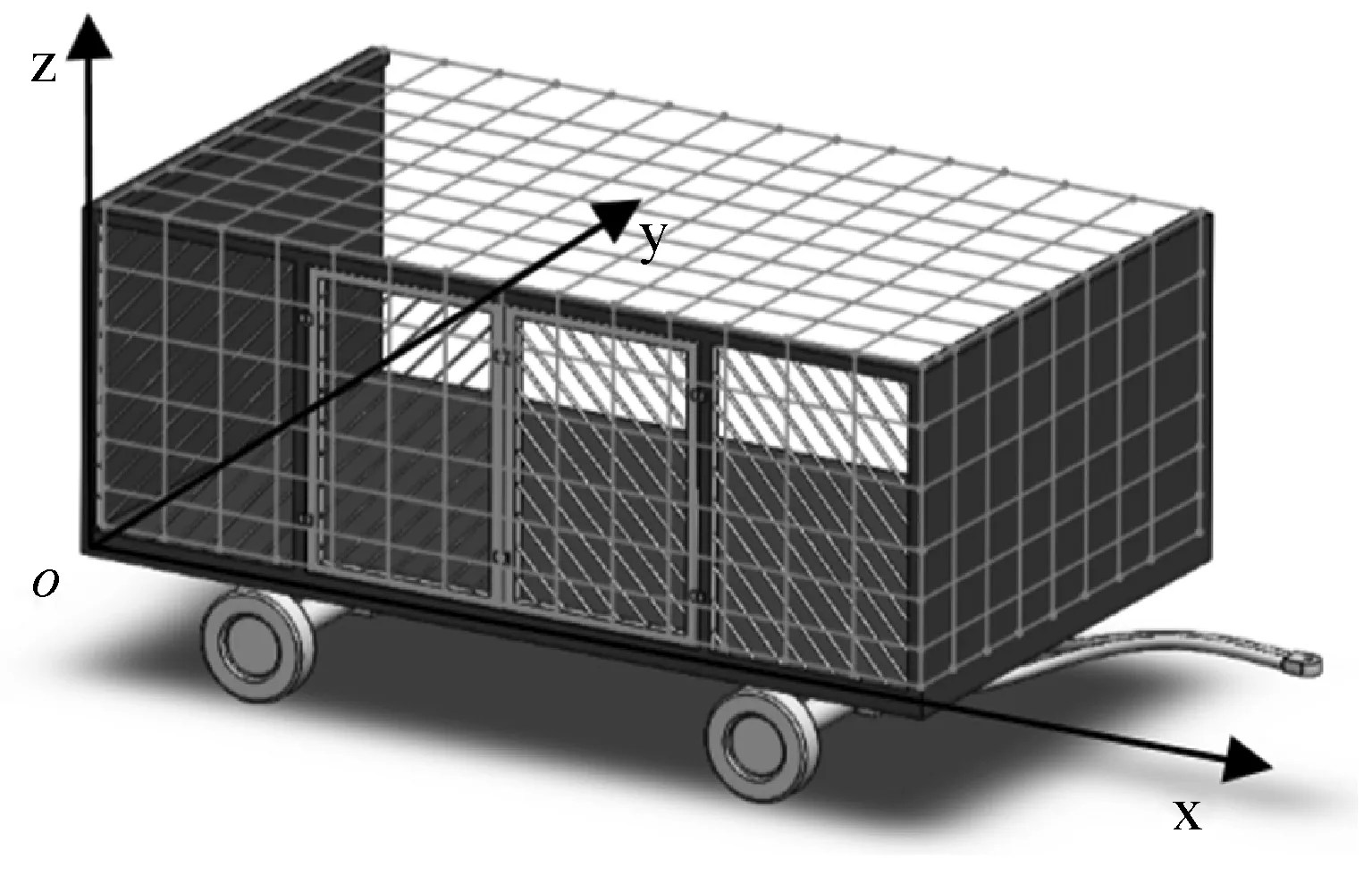
图1 行李车三维空间离散示意图

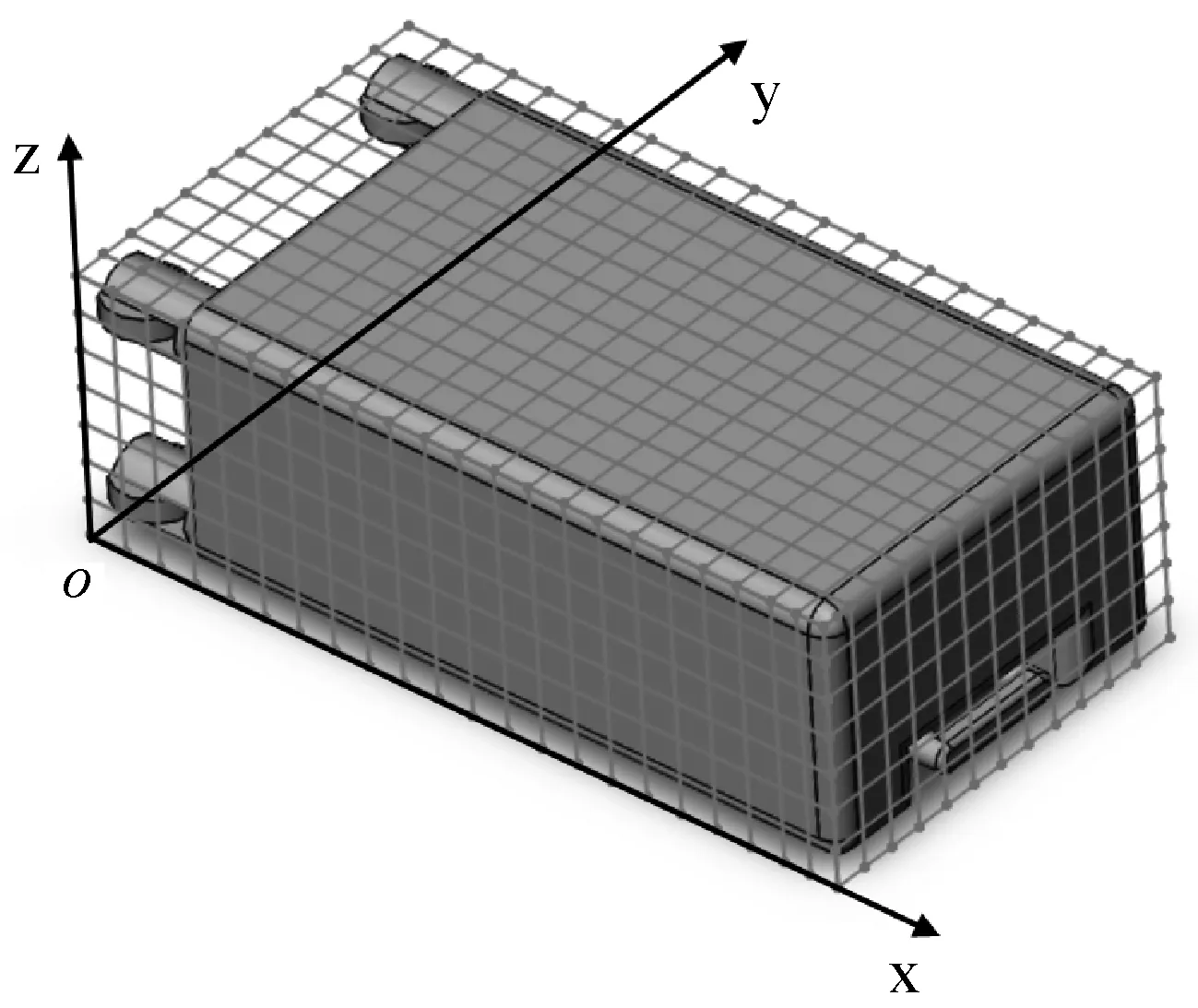
图2 行李三维空间离散示意图

考虑到三维装箱问题的复杂性，我们将三维装箱问题转化为二维平面问题，将行李车和行李的z轴忽略，将其转化为平面问题，如图3和图4所示。

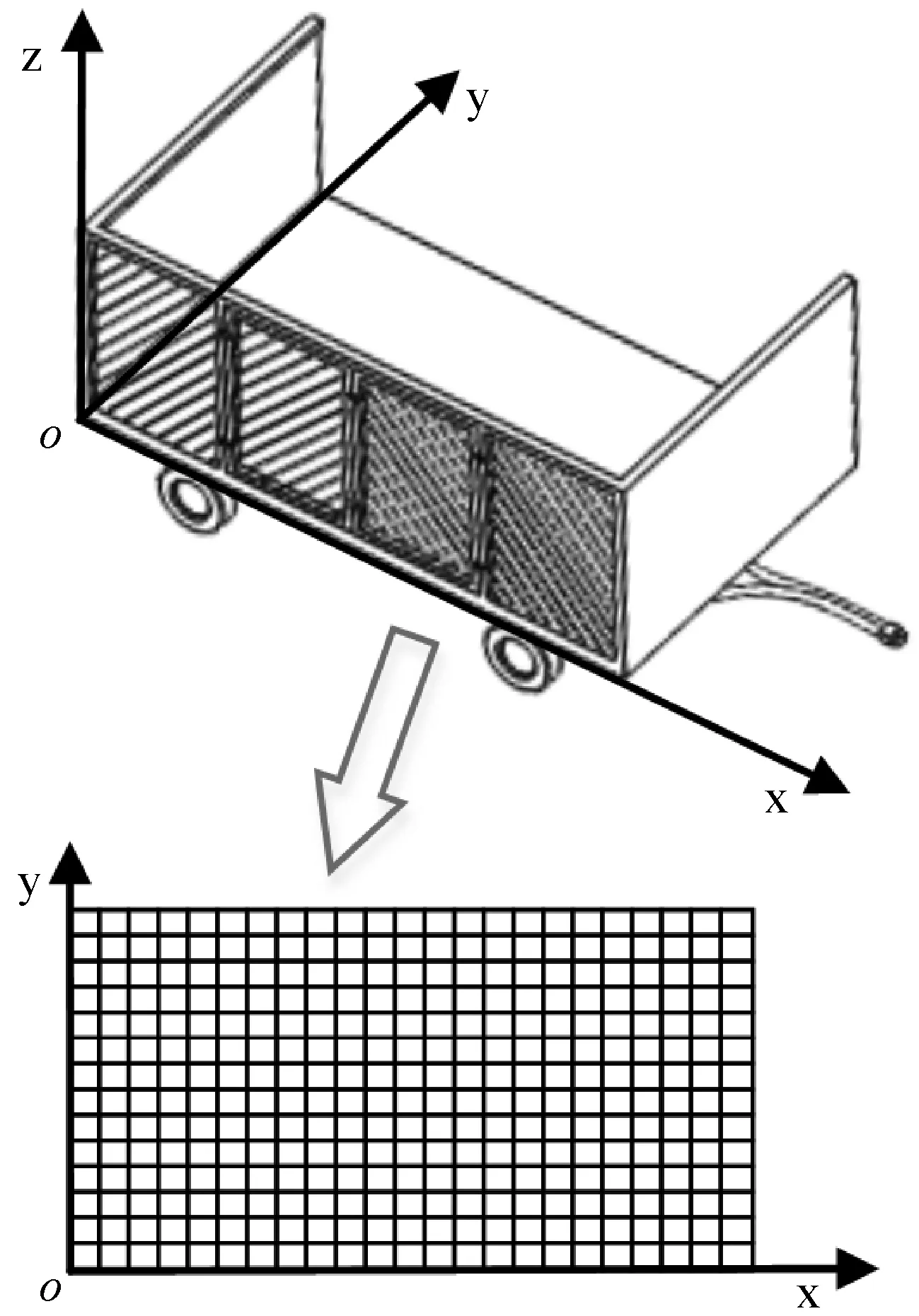
图3 行李车二维平面离散示意图

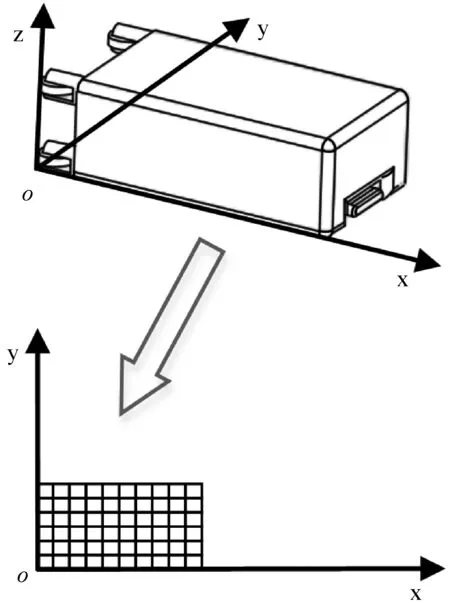
图4 行李二维平面离散示意图

在二维平面内，将行李车和行李空间离散化，沿长和宽方向等距划分为大小相等的单元网格，网格的交点为单元节点，在行李进行码放时，行李的单元网格必须与行李车的单元网格重合。行李可放位置由连续体内的无限种可能转换为单元节点个数种可能，降低了问题的复杂程度，使计算过程更加简单快速。

在行李进行码放时需要对当前所有可能码放的位置进行评价，根据评价的结果，选择最佳位置，评价方案的好坏直接影响码放结果和工作效率，因此针对行李码放策略，需要根据实际情况进行分析，确定评价方案。

(1) 当一个行李放入行李车时，该行李在二维平面内与行李车的边或者与其他行李之间接触越多，其剩余空间可能被利用的机会就会越大，这样的码放是对最终的空间利用率有利的。

(2) 当一个行李摆放后，最终整体的高度会有怎样的变化，显然高度越低，最终的效果越好，当有两个位置可选择摆放时，应该优先放置在比较低的位置上。

(3) 当一个行李摆放后，每一行的空的单元数量越多，对最终的空间利用率越不利。

(4) 行李车上摆放的行李个数越多则空间利用率越大。

以上是对评估局面需要考虑的参数的一般性描述，我们需要将其抽象为五个影响空间利用率结果的属性：

(1) 底边距：指行李在放置后，放置点距离行李车x轴垂直距离，用L表示。

(2) 行变换：对于离散后的行李车空间，在x轴方向上，从无行李放置区域到有行李放置区域是一种“变换”，从有行李放置区域到无行李放置区域也是一种“变换”，这个属性是各行中“变换”次数之和，用字母R表示。

(3) 列变换：对于离散后的行李车空间，在y轴方向上，从无行李放置区域到有行李放置区域是一种“变换”，从有行李放置区域到无行李放置区域也是一种“变换”，这个属性是各列中“变换”次数之和，用字母C表示。

(4) 空格：摆放后的空格数量之和用字母B表示，如图5所示。

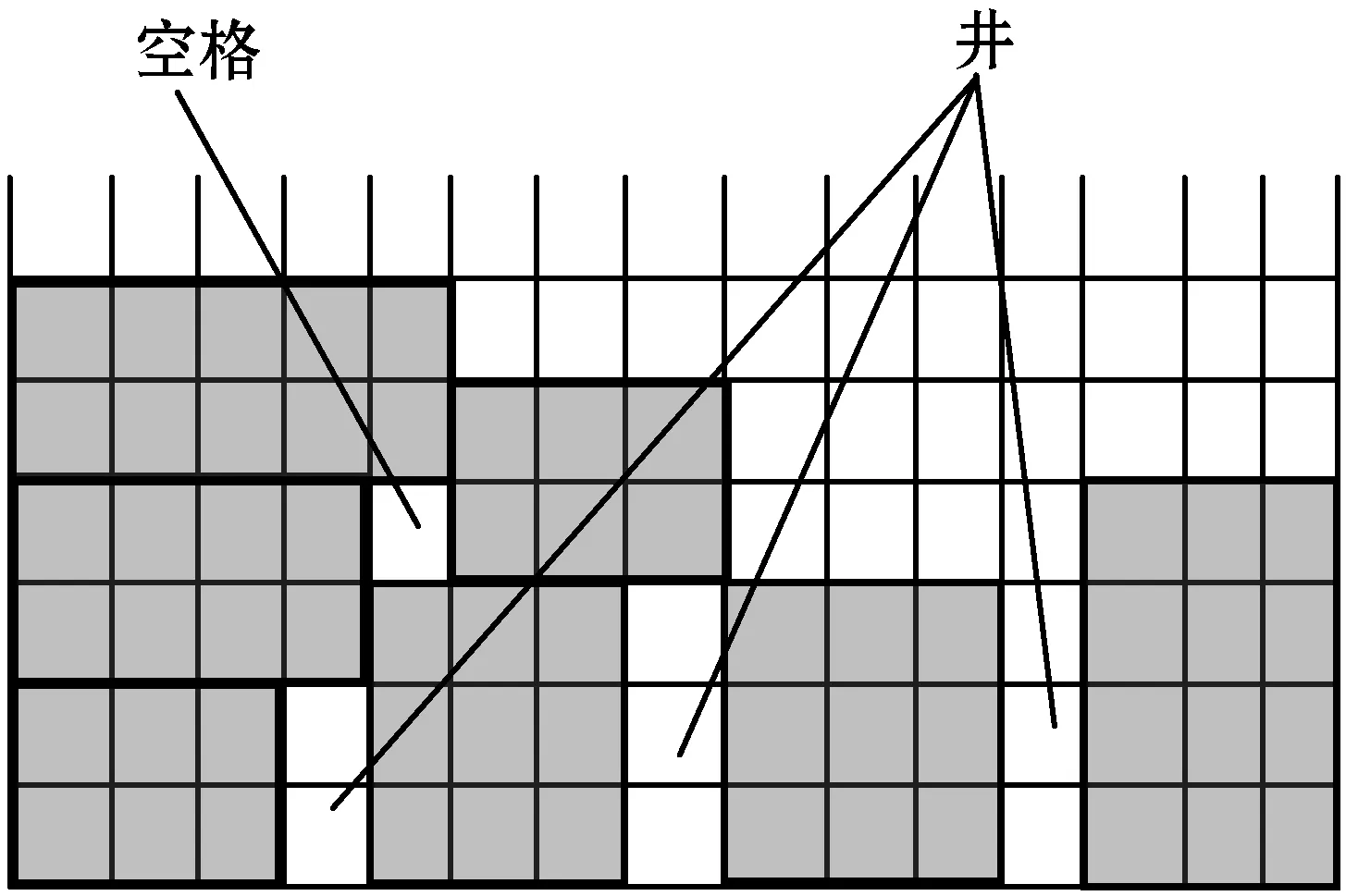
图5 “空格”与“井”示意图

(5) 井：在行李摆放后，两个行李中间，未被行李填充的单元格个数的连加和，用字母W表示。

1.2 决策过程

在行李装载过程中，需要根据实际情况考虑行李装载过程中的约束条件，根据机场的实际调研，引入以下五种约束条件：

(1) 行李方向约束：在实际装载的过程中，行李的方向约束一般分为三种，即任意方向旋转、水平旋转、不能旋转。根据行李的设计特点，行李只能沿水平方向旋转。

(2) 稳定性约束：行李在装载过程中必须得到行李车底部或者其他行李的完全支撑，不得悬空。

(3) 重心约束：在装载完毕后，行李车的重心应该在行李车的几何中心附近，有利于运输过程的稳定性。

(4) 行李最大码放层数约束：考虑运输过程中的稳定性以及最下端行李的承载能力，要对行李允许的最大码放层数限制，行李码放高度不应该超出行李车围栏的最高高度。

(5) 行李车最大载重、最大容积约束：行李车本身承载重量和最大容积的限制，已装行李的总重量不得超过行李车的最大载重量，总体积不得超过行李车的容积。

在码放过程中，在满足约束条件的情况下，第一个行李的码放通常按照“贴边”“占角”的规则进行码放，当第n个行李的位置确定后，第n+1个行李的可能码放位置就会有多种选择，在多个位置选择中选择最佳的一个位置作为行李的放置位置，这样将码放位置选择问题转换为二分类问题，即最佳码放位置为一类，其他位置为一类。在机场的实际工作过程中，一个有经验的装载工人会根据多年的工作经验合理选择下一个行李的码放位置，并且能得到较高空间利用率，因此在最佳位置选择时，根据装载工人的经验选择最佳位置，在不同布局的情况下每个可放位置的五个位置评价参数各不相同，而工人在选择最佳位置后将其单独作为最佳码放位置的类别，这样便将工人的经验映射到位置评价参数的分类选择中。例如：在图6所示情况下，深颜色为已放行李区域，浅颜色为可放位置，计算所有可放位置的评估参数，并将评估参数记录，如表1所示。根据装载工人的经验，选择最佳位置H将其标记为1，其他位置标记为-1。将其作为机器学习分类数据集进行训练，成功地将工人码放经验映射到行李参数中。

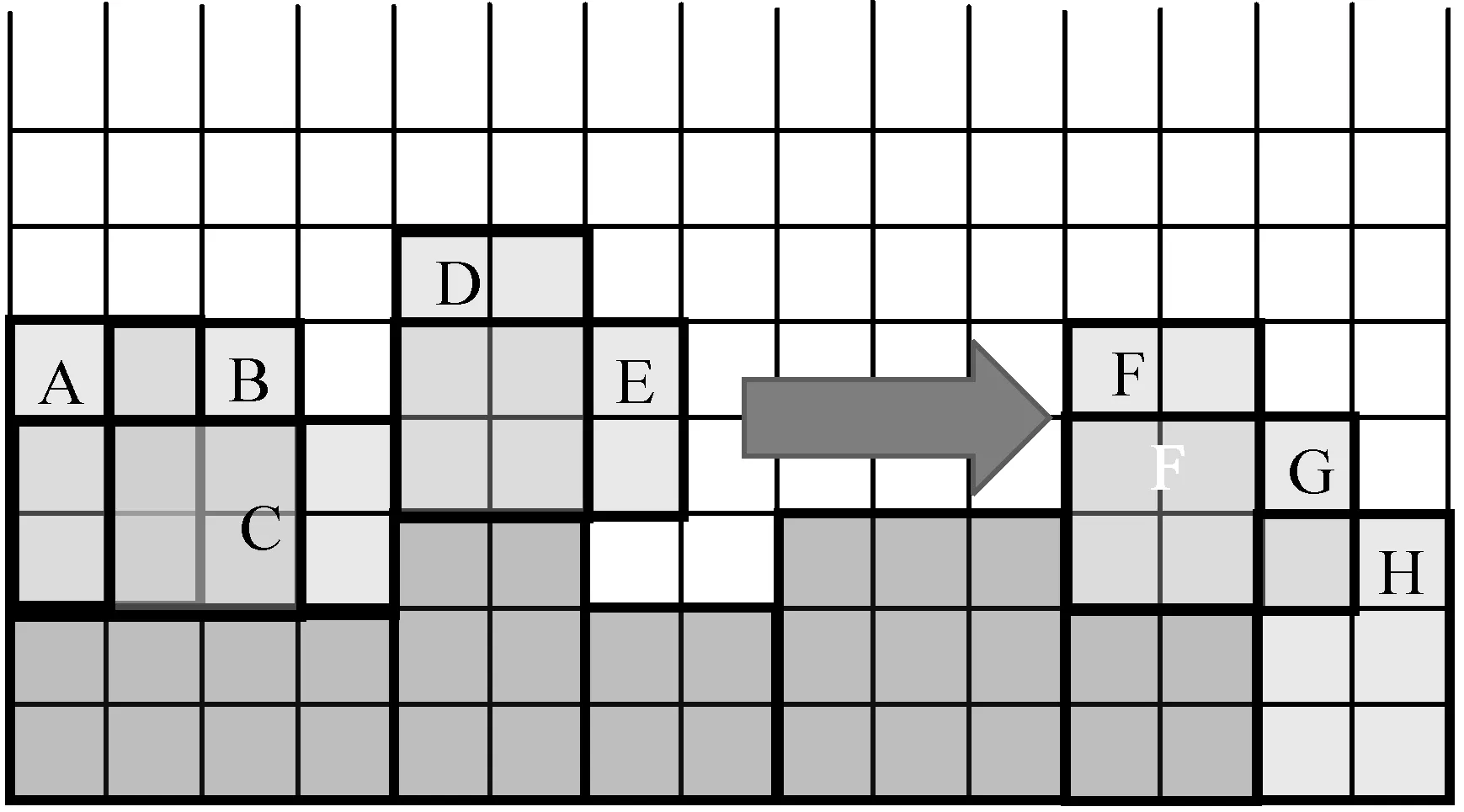
图6 第n+1个行李可放位置示意图

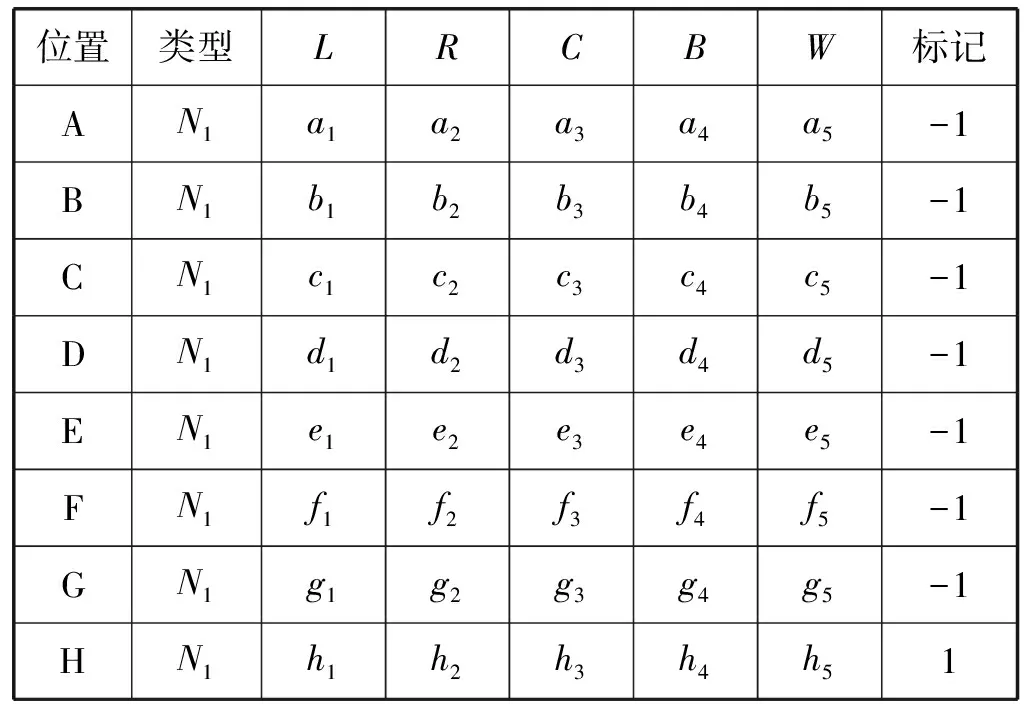
表1 不同码放位置各参数取值

2 学习算法

在模型训练过程中，根据装载工人的经验，对可放位置进行标记，将可放位置分为两类，将选择最佳位置作为机器学习的输出，这样行李位置的选择问题转化为二分类问题，针对二分类问题，支持向量机模型得到广泛应用，并且可以得到较高的分类准确率。

2.1 支持向量机模型

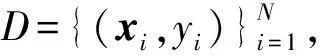
(1)

根据最小优化原则可以求得优化目标α，所以得到分类函数：

(2)

2.2 深度支持向量机模型

深度支持向量机(Deep Support Vector Machine， DSVM)由输入层、中间层和输出层组成，每层都是一个完整的支持向量机，其中间层的数量为l层，结构如图7所示。训练样本通过上一层的训练得到支持向量，并将每次训练结果经过处理作为下一层训练的输入，从而构建一层新的训练模型。

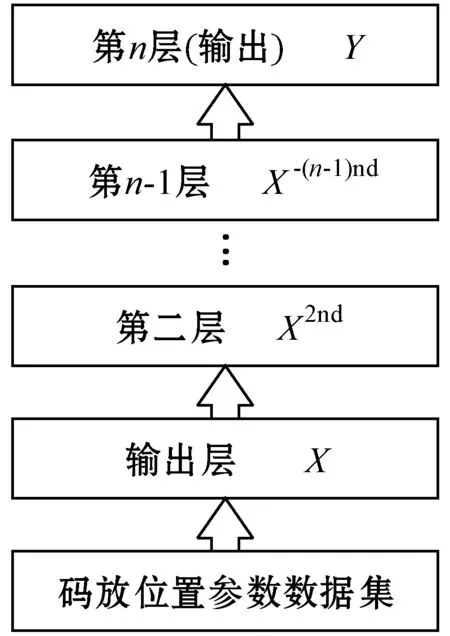
图7 深度支持向量机模型

g(i)=ysviaiκ(xvi,x)+bi=1,2,…,Q

(3)

式中：svi为支持向量；ai为对应的拉格朗日因子；ysvi为支持向量对应的标签；b为偏置。

在经过降维处理后可以得到的样本可以表示为：

ysvQaQκ(svQ,xi)+b}

(4)

对于测试样本集，也使用照降维公式逐层对其映射，其分类判别函数为：

(5)

2.3 深度稀疏最小二乘支持向量机

DSVM方法与传统SVM方法比较，在对码放行李参数训练时，虽然能够得到较高的准确率，但是随着训练层数的增加，训练过程中计算的复杂程度和训练时间也随之增加。最小二乘法支持向量机模型可以将不等式约束转换为等式约束，降低计算的复杂程度，但是在求解的过程中模型会对每个样本进行训练，缺少稀疏性，因此，提出深度稀疏最小二乘支持向量机模型来解决此问题。通过求解样本数据高维特征空间近似最大线性无关向量组的方法对其进行稀疏化处理，在保证分类准确率的同时，增加了训练样本的稀疏性，提高了计算效率。

在对最小二乘支持向量机稀疏化的过程中主要包括两个步骤。

(1) 寻找高维空间的一组近似线性无关向量，构造线性向量组，对位置参数样本进行稀疏表示。

首先寻找码放位置参数样本的特征子集B={(xj,yj)}j∈s⊂D,m=|S|≤N，使所有的样本可以表示成该特征子集在特征空间的线性组合：

(6)

所以可得：

(7)

因此，分类判别函数表示为：

(8)

通过选择参数v来去除特征空间中的近似相关向量，同时也可以控制子集B与样本的逼近程度，稀疏化的流程如图8所示。

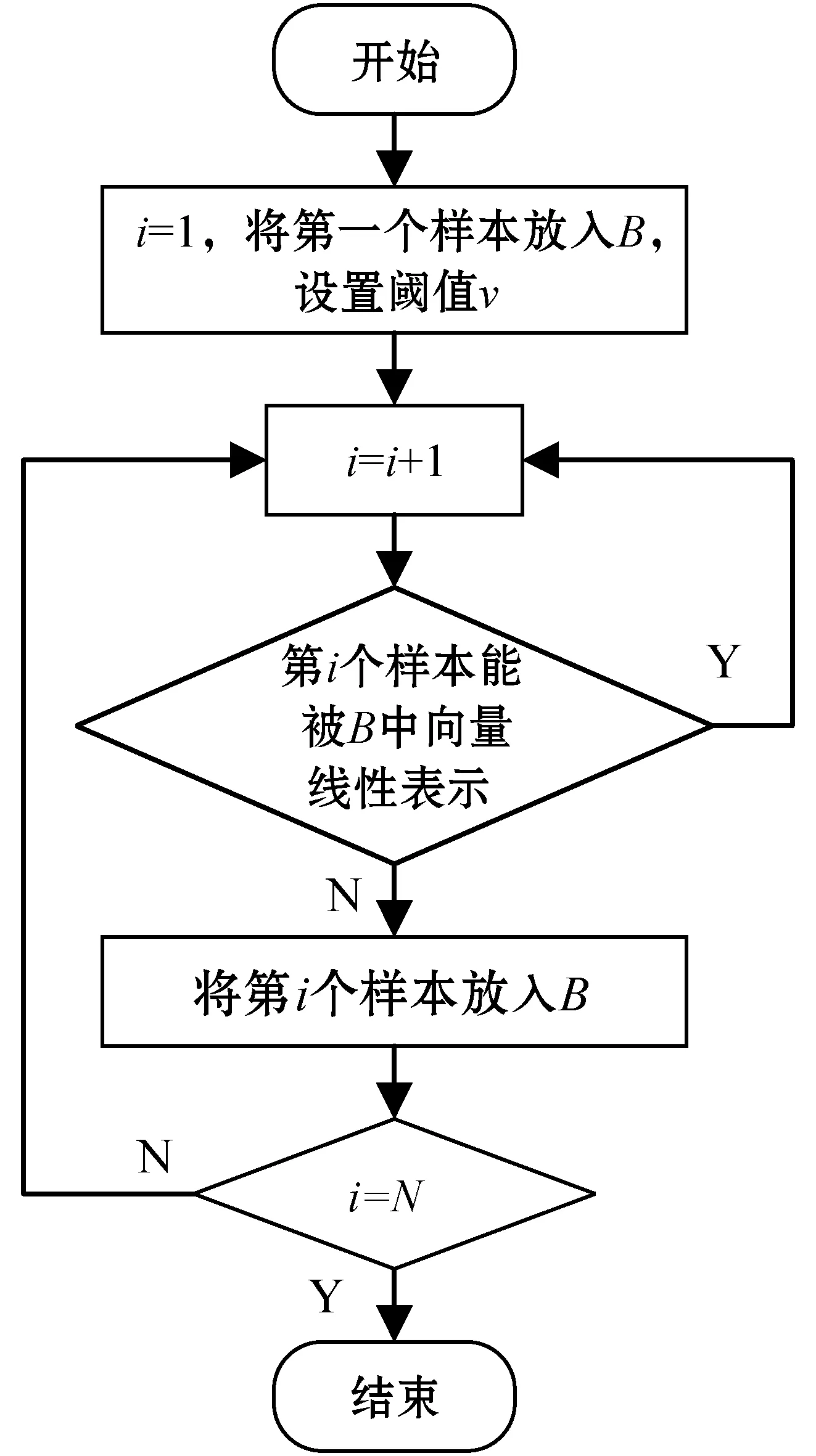
图8 稀疏化流程

(2) 利用稀疏样本求解最优分类判别函数。将式(7)、式(8)代入最小二乘支持向量优化目标函数中，可得：

(9)

式(9)是关于β和b的凸二次规划问题，其中：β=[βS1,βS2,…,βSm]；ym=[yS1,yS2,…,ySm]∈Rm；D(ym)为以ym元素为对角元素构成的对角矩阵；(Kmm)i,j∈S=κ(xi,xj)=Φ(xi)TΦ(xj)；yN=[y1,y2,…,yN]∈RN；D(yN)为以yN为对角元素构成的对角矩阵；KNm=[km(x1),km(x2),…,km(xN)]T；km(xj)=[κ(xi,xS1),κ(xi,xS2),…,κ(xi,xSm)]T；1为元素全为1的单位列向量。最优解可以通过以下条件求得：

(10)

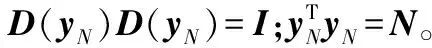
对其求解可得关于β和b的方程组：

(11)

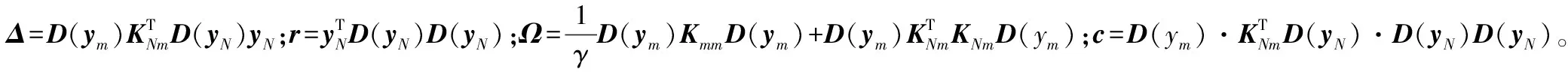
2.4 算法实现

在算法实现过程中，只需将深度支持向量机中的每一层替换为SLSSVM即可，实现多层最小二乘支持向量机的叠加，训练过程与DSVM相同，首先使用SLSSVM的输入层对初始样本进行训练，然后使用降维公式对输出层的结果进行处理，并将处理结果作为第二层的输入进行训练，而DSLSSVM利用SLSSVM的系数β与向量组B构造降维公式，这里降维公式可以表示为：

g(i)=ysvjβiκ(xj,x)+bj∈S

(12)

随后逐层训练，直至输出结果。通过DSLSSVM深层结构对细腻码放位置参数进行训练，对其内在规律进行学习，既可以得到较高的识别准确率，又可以减少运算时间。

3 仿真实验

3.1 实验配置

本实验使用计算机主要硬件配置如表2所示。

表2 计算机主要硬件配置

仿真实验使用计算机运行的操作系统为Microsoft Windows 7，本实验中的算法均使用Python语言进行编写，在机器学习方面使用scikit-learn模块来实现，使用pandas和numpy数据库对数据进行处理。

3.2 训练数据

根据国际航空运输协会(International Air Transport Association，IATA)规定，随身登机箱尺寸三边之和不得超过115 cm，托运行李箱尺寸不得超过158 cm，所以20英寸及以下的行李箱可以随身带入机舱，28英寸及以下的行李箱可以进行托运，现假设行李的类型为4种，分别为22英寸(60 cm×35 cm×22 cm)、24英寸(65 cm×40 cm×26 cm)、26英寸(70 cm×45 cm×28 cm)和28英寸(75 cm×50 cm×32 cm)；根据调研，目前机场采用的行李拖车大多数为三面护栏式行李拖车全车尺寸为300 cm×175 cm×100 cm。

在仿真实验中，我们将仿真过程分为两个阶段，即训练阶段和工作阶段。在训练阶段，数据集由计算机自动生成，首先系统会随机生成要码放行李类别，计算机根据当前行李车布局情况，沿x轴方向依次遍历所有可放位置并计算每个位置评估参数数值，每个位置生成一组数据，有经验的码放工人根据多年工作经验选择最佳位置进行码放，计算机将此位置进行标记，完成一个行李的码放，重复以上过程直至整个行李车被装满，生成训练数据集。

3.3 不同分类模型对比实验

为了验证本文使用的DSLSSVM分类模型优于其他模型分类准确率，分别使用DSLSSVM、SVM、决策树分类模型和朴素贝叶斯分类模型进行对比实验。使用三组不同的行李码放位置参数作为样本进行实验，每组实验包括5 000组数据，分别使用不同算法进行实验，实验结果如表3所示。

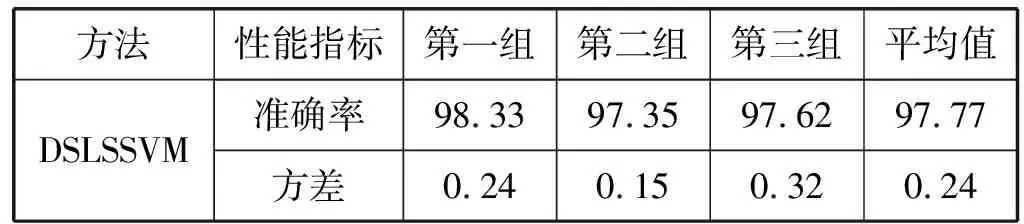
表3 准确率统计表(%)

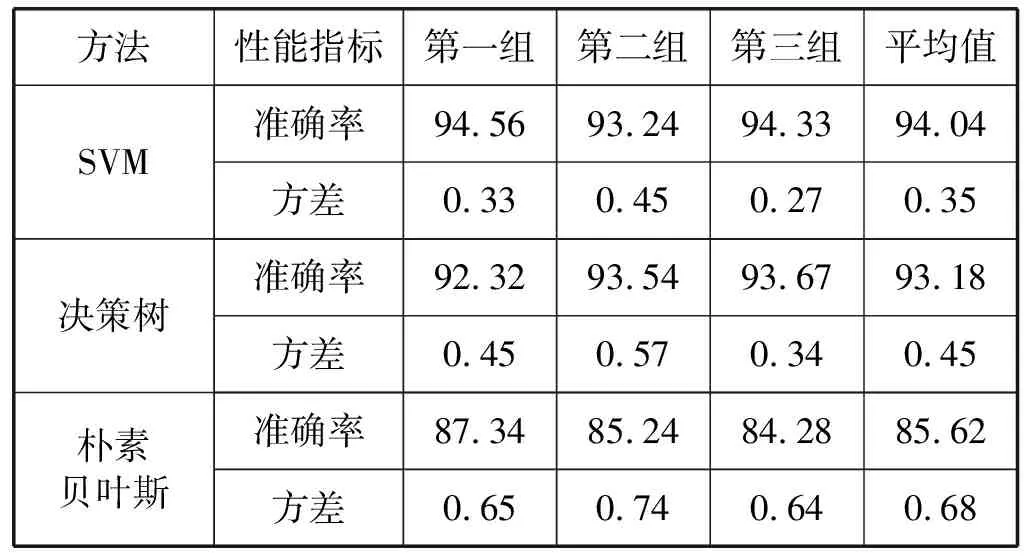
续表3

可以看出，在本文的分类实验中， DSLSSVM分类准确率最高，达到97.77%以上，比SVM分类模型的分类精度高3.73百分点，比朴树贝叶斯分类模型高12.15百分点，所以DSLSSVM分类算法模型适用于本文的空间离散算法，并且可以满足精度要求。

3.4 利用率对比实验

在确定了DSLSSVM分类模型的可行性后，将训练数据集定为8 000组，使用10折交叉验证法对DSLSSVM分类模型进行训练，并将训练好的模型保存。在利用率对比实验中，使用训练好的模型进行仿真实验，图9分别给出使用人工经验码放、基于机器学习的空间离散算法码放、依次横放、依次竖放和传统的启发式算法五种不同的码放方法下得到的二维装箱效果图。

(a) 人工经验码放仿真图

使用人工经验进行码放仿真时，通过Python语言进行编写程序，使用计算机输入设备键盘的方向键控制行李在行李车网格空间中的位置，模拟工人装载的过程，通过工人日常积累的经验根据行李的大小和行李车的布局情况调整行李码放位置，将行李放在当前布局情况下最佳码放位置，完成一次码放。

传统的启发式算法在解决装箱问题时大多采用“分层”和“分块”的概念，本文在进行仿真实验时根据文献[18]提出的基于“块”和“空间”的启发式算法，对其算法进行复现，作为对照进行仿真实验。

在实验过程中，分别使用人工经验码放、基于空间离散算法的码放策略、行李依次横放、行李依次竖放和传统启发式算法的方式进行码放实验，每种码放方式进行三组实验，每组实验各码放十次，统计其利用率如表4所示。

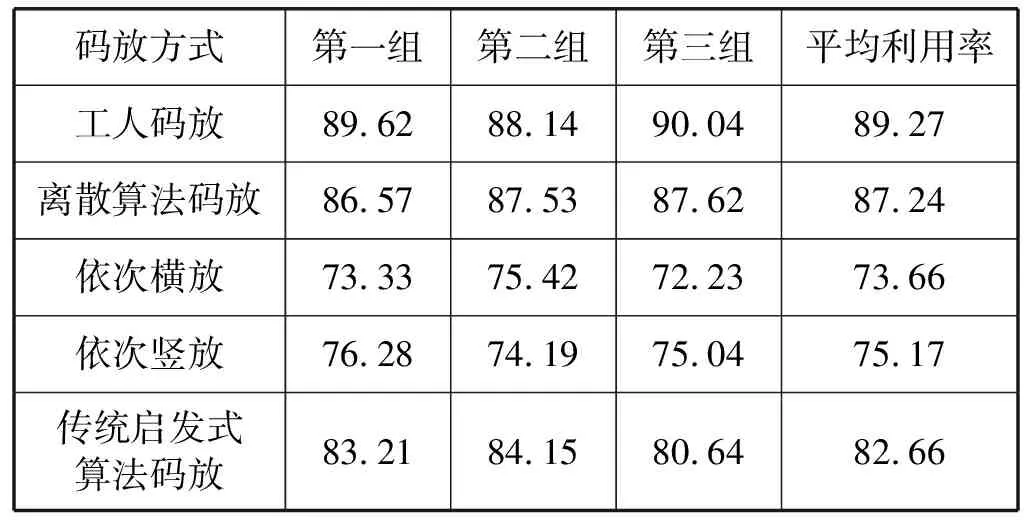
表4 利用率统计表(%)

通过与工人经验码放的对比实验可以看出，本文提出的空间离散的概念可以有效地将工人经验映射到评价参数中，同时证明了本文提出的基于深度稀疏最小二乘支持向量机分类模型可以实现对行李参数的准确分类，适用于空间离散算法。使用空间离散算法得到的空间利用率达到87.24%，接近有经验的工人的码放水平。与其他码放方式进行对比可以看出，比传统启发式算法得到的仿真结果高4.58百分比，比行李依次竖放利用率提高了12.07百分比，比依次横放利用率提高了13.58百分比。综上所述，该算法可以代替机场工人实现行李的自动化装载，并且可以达到与人工码放行李较为接近的水平，与其他码放方式相比可以得到较大的空间利用率，满足机场高效运输的基本要求。

3.5 运算时间对比实验

在机场实际装载的过程中，除了满足空间利用率最大原则外还要考虑算法计算速度尽可能快，满足在线码放的要求。传统的基于“块”和“空间”的启发式算法在进行码放位置的选择时，采用启发式搜索的方法遍历所有可能码放的位置，同时还将剩余的空间进行选择、划分、合并，更是增加了可放位置的选择，使得算法计算更加复杂，耗费大量时间。

使用本文提出的基于空间离散的机场行李码放策略与基于“块”和“空间”的启发式算法的码放方法在相同的情况下进行行李码放作业，统计两种不同算法装入行李个数如表5所示。

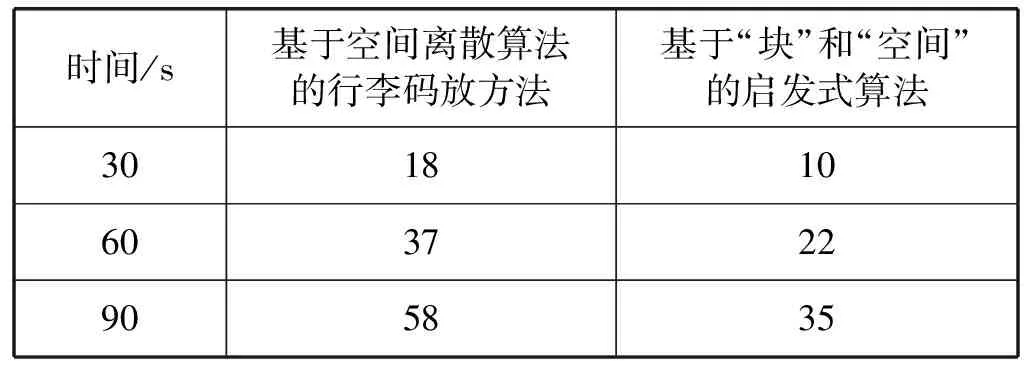
表5 相同时间下装入行李个数统计表

可以看出，在本文提出的基于空间离散算法的机场行李码放策略在相同时间码放行李个数远大于基于“块”和“空间”的启发式算法码放的行李个数，并且对行李车的空间利用率较高，所以与传统基于“块”和“空间”的启发式算法相比，本文算法更适合机场高速、高效率的要求。

4 结 语

为了解决机场行李在转运过程中存在的装箱问题，提出一种基于空间离散算法的机场行李码放方法。通过分析机场行李码放特点，定义行李码放位置的评价参数，模拟有经验工人的码放过程，构建训练样本，使用DSLSSVM模型学习工人经验，得到训练模型。在实际工作中，系统根据行里车内不同局面给出不同的码放方案，完成行李在线实时码放。

仿真实验结果表明，通过该方法码放的行李在空间利用率和效率方面可以达到与人工码放行李比较接近的水平，可以满足机场行李运输的要求。并且相比于基于“块”和“空间”的传统启发式算法，该方法在实现过程中减少了算法计算时间，提高了机场行李装载效率，具有较强的实用性。