基于SAE与CEEMDAN-BiLSTM组合模型的短期电力负荷预测

黄 炜 陈 田

(上海电机学院机械学院 上海 200120)

0 引 言

近年来，随着我国科技工业的高速发展，电能的需求量不断增大，对于电力负荷预测准确度的要求也在不断地提高。按照时间跨度的不同，负荷预测主要分为超短期、短期、中期和长期，其中短期负荷预测主要对未来24小时或者数天时间内的用电负荷进行预测[1]，它对于发电机的投切、机组的检修安排、电力营销等有着重要意义，精准的负荷预测有利于发电设备的充分利用，能有效降低电网的运营成本[2]。

国内外对于负荷预测算法的研究工作有许多，其中具有代表性的算法主要包括：支持向量[3]、随机森林[4]、卡尔曼滤波法[5]与人工神经网络[6]等。文献[7]使用粒子群算法对反向神经网络进行初始化，并且引入了遗传算法，优化网络初始权值，从而提高了模型的性能。文献[8]将深度信念网络模型(DBN)与支持向量机(SVR)相结合，使得模型具有更高的准确性。文献[9-10]探讨了BP神经网络在负荷预测中的应用，文献[11]使用了模糊神经网络进行负荷预测。文献[12]采用了EMD算法对负荷数据进行分解，然后对于分解得到的各个平稳分量建立预测模型，最终在更加平稳的分量中取得了更高的精度。文献[13]和文献[14]分别通过改进的果蝇算法和粒子群算法优化BP神经网络权值和阈值，从而提高预测精度。但是传统的神经网络没有考虑到负荷在时间序列上的关系，所以在一定程度上不能很好地拟合时间序列上的负荷曲线。

长短期记忆网络((Long Short-term Memory,LSTM)同时兼顾非线性与时序性，被广泛应用于语音识别、机器翻译等领域[15]。基于电力负荷在时间序列上的特性，文献[16]提出用LSTM神经网络进行负荷预测，最后经实验表明LSTM的预测精度比其他模型的精度高。文献[17]使用CNN对负荷数据进行降维，然后将降维后的数据作为LSTM的输入，这在一定程度上提高了LSTM的预测精度。

鉴于上述模型都无法对预测结果进行误差修正，本文提出SAE与CEEMDAN-BiLSTM组合的短期电力负荷预测模型，算法首先使用SAE模型学习负荷序列的主要特征，误差特征主要体现在SAE模型预测过程中所产生的误差序列中；然后使用CEEMDAN算法将误差序列分解为数个IMF分量与残余分量，建立BiLSTM模型学习每个误差分量的时序特征，将各个分量的BiLSTM模型的预测值相加得到误差的预测值；最后使两部分的预测值相加从而达到修正误差的效果。实验结果表明：SAE与CEEMDAN-BiLSTM的组合模型具有更好的预测精度，能够为电力系统的调度和生产计划提供更加有效的科学依据。

1 SAE与CEEMDAN-BiLSTM的组合模型

1.1 栈式自编码器

自编码器(autoencoder，AE)作为栈式自动编码器(Stacked AutoEncoder,SAE)的基本组成部分，其结构类似于三层神经网络，是一种无监督学习，主要由输入的编码器与输出的解码器构成，一般用于数据的降维与去噪，功能类似于主成分分析PCA。如果使用适当的维度和稀疏性约束，会得到比PCA更好的数据投影效果。自编码器的输入节点等于输出节点，通过一个恒等的函数，可以对数据进行重构。

对于输入的编码器，其计算公式如下：

y=f(Wx+b1)

(1)

式中：y表示编码器的输出；x表示解码器的输入；f表示激活函数，一般为Sigmoid函数；W和b1分别表示输入层到隐藏层的权重与偏置。

对于输出的解码器，其计算公式如下：

z=f(WTy+b2)

(2)

式中：z表示解码器的输出；WT和b2表示输入层到隐藏层的权重与偏置。这样通过调整网络的参数，可以使最终输出的z尽可能地接近于自编码器输入的x，从而达到重构输入数据的目的。

自编码器通过反向传播的方式使重构的误差最小，与传统神经网络一样，自编码器也是通过最小化损失函数来调整网络结构中的参数，损失函数的公式如下：

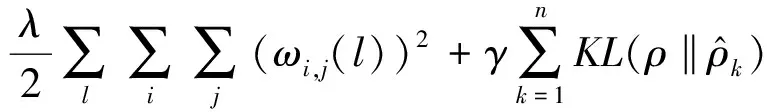
(3)

栈式自动编码器由多个自编码器堆叠而成，其训练过程一般分为无监督预训练阶段和有监督训练阶段。在无监督预训练阶段，它可以逐层提取数据的高阶特征，逐步降低数据的维度，将复杂的数据转化为简单的特征序列。在有监督训练阶段，栈式自动编码器将无监督训练过程中得到的特征序列输入到一个分离器中进行分类。SAE的训练过程主要分为以下三步，如图1所示。

图1 SAE的训练过程

(1) 首先使用自编码器训练从输入层X到隐藏层H之间的参数，训练结束后，去除自编码器的输出层x,接着将AE1的隐藏层H的输出作为AE2的输入,采用相同的办法训练自编码器AE2。

(2) 重复步骤(1)，直到初始化所有的自编码器参数。

(3) 将最后一个自编码器隐藏层的输出连接到分离器中，以有监督的方式进行训练。

1.2 CEEMDAN原理

CEEMDAN在EEMD分解的过程中添加自适应的白噪声并且计算唯一的余量信号以获取IMF分量，可以在较少的实验次数中对信号进行序列重构，消除了EEMD分解过程产生的残余信号中由于添加自适应白噪声所产生的误差。

定义计算符Ei()表示使用EMD分解产生的第i个IMF分量，CEEMDAN算法的计算步骤如下。

(1) 在k次实验中，对原始信号xt+δ0ωj进行分解，其中：δ0表示高斯白噪声的标准差；ωj表示高斯白噪声。通过EMD分解得到第一个IMF分量并获取唯一的余量信号r1(t)。

(4)

r1(t)=x(t)-IMF1(t)

(5)

(2) 继续获取第二个IMF分量：

(6)

(3) 重复以上步骤，计算第n个余量信号：

rn(t)=rn-1(t)-IMFk(t)

(7)

则第n+1个IMF分量为：

(8)

(4) 重复步骤(3)，直到余量信号呈单调趋势，分解停止原始信号x(t)被分解为：

(9)

式中：N为最终模态分量的个数；r(t)为最终单调的余量信号。

1.3 LSTM循环网络

图2 LSTM结构

LSTM在每个隐藏层内都接收上一时刻的输出和当前时刻的输入及当前的隐藏层状态，并且通过输入门、遗忘门、输出门来控制和更新当前隐藏层的状态，最后将更新结果输出。计算公式如式(10)-式(15)所示。

ft=σ(Wf·[ht-1,xt]+bf)

(10)

it=σ(Wi·[ht-1,xt]+bi)

(11)

(12)

(13)

ot=σ(Wo·[ht-1,xt]+bo)

(14)

ht=ot*tanh(ct)

(15)

式中：Wf、Wi、Wc和Wo分别表示遗忘门、输出门、记忆状态和输出门的权重矩阵；bf、bi、bc和bo分别表示对应的偏置向量；σ为激活函数Sigmoid；*表示点乘。

1.4 BiLSTM算法

首先使用EMD算法将负荷数据分解为数个本征模态函数(IMF)与残余分量r(t)，然后对于每个分量建立BiLSTM模型。BiLSTM是由前向LSTM网络与后向LSTM网络构成，其结构如图3所示。

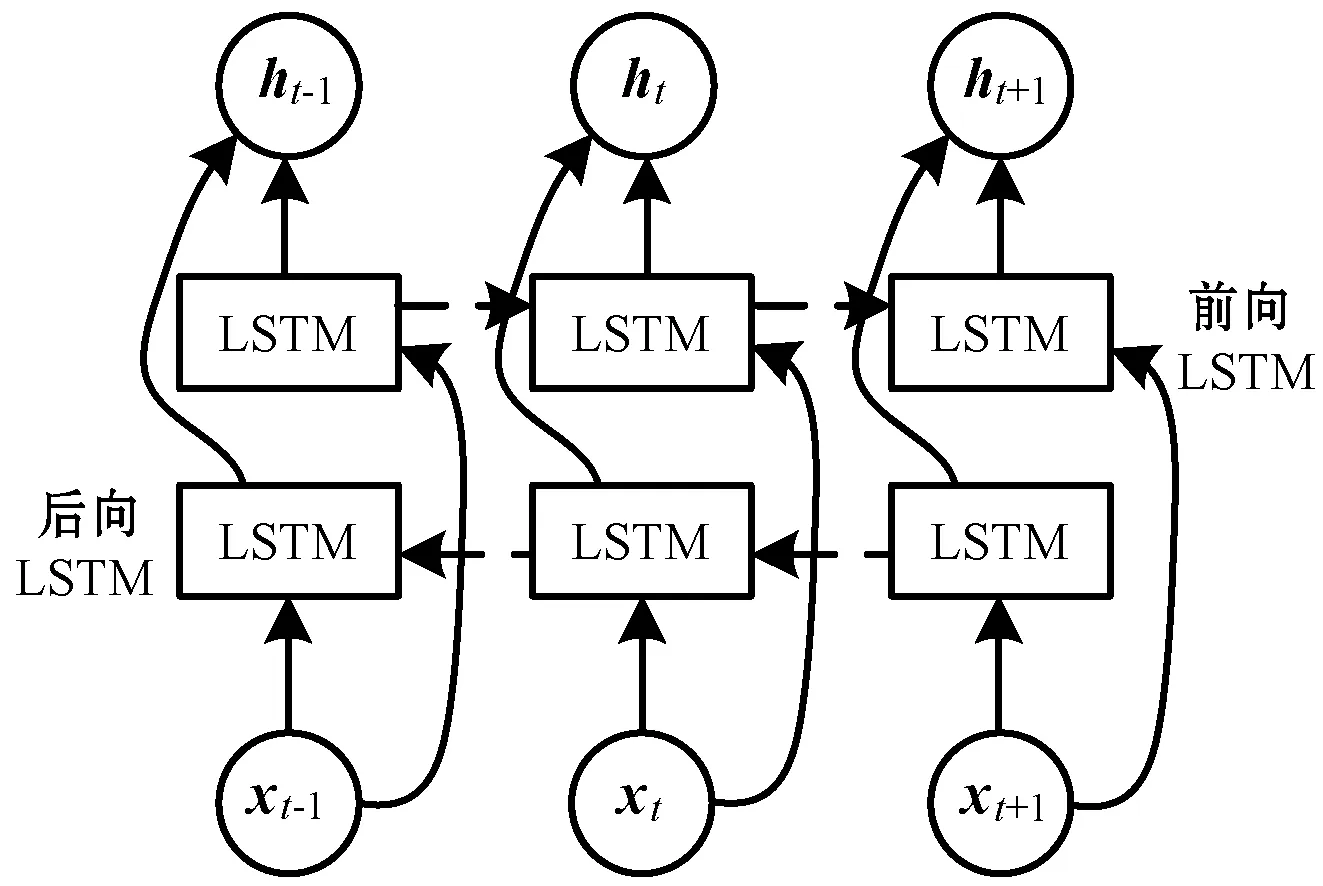
图3 BiLSTM结构

BiLSTM神经网络会基于整个时间序列作出预测，它将隐藏层划分为前向与后向两个对立的部分，分别读取过去与未来时刻的信息。第一层前向LSTM计算当前时刻序列的顺序信息，第二层后向LSTM计算相同时刻序列的逆序信息，最后BiLSTM在t时刻的隐藏层状态由前向隐藏层状态和后向隐藏层状态加权得到。其计算公式如下：

(16)

(17)

(18)

2 实验数据

现有美国某电力市场2015年的样本数据集，数据集的采样周期为30 min。实验所用特征包括：负荷值、气象因素、节假日类型和气温。实验数据如表1所示。

表1 实验数据

部分数据用虚拟编码模式表示，以{0，1，2}表示{工作日，休息日，节假日}。降雨{有，无}表示为{0，1}。

实验采用全年数据集6月至8月共计92天的数据作为训练集，以9月1日至9月11日的数据共计11天的数据作为测试集，以历史48个时刻点的数据预测未来48个时刻点的负荷数据。

将93天的训练集转化为的三维矩阵，三维矩阵的维度信息为：

{D1D2…D92}×{L1L2…L48}×{X1X2…X8}

(19)

式中：{D1D2…D92}表示数据集长度为92天；{L1L2…L48}表示每天所包含的48个时刻的数据；{X1X2…X8}表示数据集的8维特征。

同理，测试集的维度信息为：

{D1D2…D11}×{L1L2…L48}×{X1X2…X8}

(20)

同时BiLSTM与其他机器学习预测方法一样，对数据的尺度比较敏感，所以这里采用MaxMin的方法对数据进行归一化处理，将所有数据的值域归一化到[0,1]范围内，然后将归一化的数据传入到模型中，最后将模型的输出结果进行反归一化，计算的公式如下：

(21)

3 算例分析

3.1 SAE-CEEMDAN-BiLSTM模型计算流程

(1) 负荷预测。使用包含气象因素、工作日类型的训练集对SAE模型进行有监督训练，待模型收敛后对训练集与测试集进行预测，得到测试集的预测值Pb，并且根据下式得到SAE训练过程中产生的误差序列Pe：

Pe=Pbtrain-Ttrain

(22)

式中：Pbtrain为训练集的预测值；Ttrain为训练集的真实值。

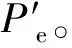
(3) 计算组合模型的预测值。SAE-CEEMDAN-BiLSTM模型的预测结果P为测试集的预测值与误差的预测值之和，即：

(23)

SAE与CEEMDAN-BiLSTM组合模型的预测流程如图4所示。

图4 预测流程

3.2 模型训练方法

模型的训练过程采用Adam优化算法。Adam结合了RMSprop善于处理非平稳目标与Adagrad善于处理稀疏梯度的优点，其计算公式如下：

mt=μ*mt-1+(1-μ)*gt

(24)

(25)

(26)

(27)

(28)

式中：gt表示梯度；为平滑指数，主要用于防止分母为零；μ与v表示动量因子；mt与nt是对梯度的一阶矩阵估计，可以看作是对期望E|gt|和的估计；与是对mt与nt的修正，这样就可以对期望进行近似的无偏估计。

3.3 模型的评价指标

模型的评价指标通常采用平均绝对百分误差(Mean Absolute Percentage Error,MAPE)，其计算的公式如下：

(29)

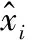
3.4 SAE模型训练与预测

实验在Ubuntu 18.04系统下利用Pytorch1.10完成，实验PC的处理器为Inter Core i5- 8300H，内存为16 GB，显卡为NVIDIA GeForce GTX 1050TI。

在无监督训练阶段，将SAE中的自编码器基本单元个数设置为3，每个自编码器输入节点个数为48，隐藏节点为16，激活函数设置为ReLU，设定学习率η=0.1，最大迭代次数n=40 000。在有监督训练阶段，将分离器的输出节点设置为48,以梯度下降的方法对网络参数进行优化。

SAE模型收敛后，将训练集中的数据按照时间先后顺序依次输入至训练完毕的模型中，得到训练集的预测结果Pbtrain，如图5所示。同时根据式(22)可以求得SAE模型在预测过程中产生的误差序列Pe，如图6所示。

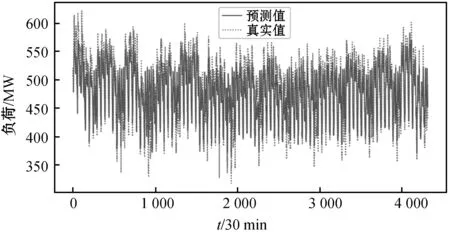
图5 SAE模型的预测结果

3.5 CEEMDAN误差序列分解

设定CEEMDAN算法的总体集成次数为400，加入白噪声标准差为0.2，利用CEEMDAN算法将Pe分为9个IMF分量与1个残余分量，实验仿真结果如图7所示。

图7 CEEMDAN分解结果

可以看出，IMF1-IMF4分量的频率较高且周期性不明显，可以看作负荷序列的高频分量。IMF5-IMF7分量的周期性明显，可以看作负荷序列的周期分量。IMF8、IMF9分量的频率较低且周期性不明显，可以看作负荷序列的低频分量。Residual为序列的残余分量。

3.6 BiLSTM网络结构设计

将CEEMDAN算法分解得到的9个IMF分量与1个残余分量分别建立BiLSTM模型，将前向LSTM与后向LSTM输入节点设置为1，表示每次读取一个时刻点的负荷数据，将隐藏层节点设置为12，分别为当前时间点前后12个时刻的误差信息。将输出节点设置为1，为第13个时间点的误差预测值。设置学习率为0.001，同时为BiLSTM网络的输出层再加上一层线性全连接层，激活函数设置为tanh。

设定BiLSTM模型的训练方式为：通过历史48个时刻点的误差序列预测未来48个时刻点的误差序列，因此以6月1日至8月30日的误差序列作为网络的输入，以6月2日至8月31日的误差序列作为网络的输出，以Adam算法训练网络。BiLSTM网络参数如图8所示，以BiLSTM层的输入层为例，{91,48,1}={输入数据集长度为91天，每日包含的48个时刻点，当前时刻的误差值}。

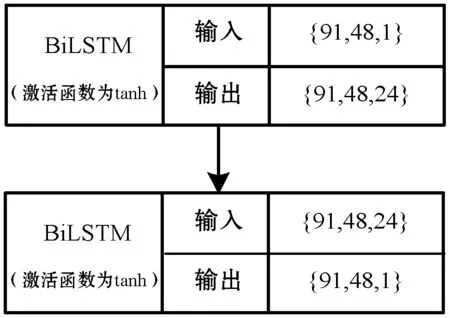
图8 BiLSTM网络结构

3.7 预测分量重构

将各个IMF分量ci(t)以及残差分量rn(t)的预测值进行累加得到误差的预测值,如式(30)所示。

(30)

式中：p(t)为重构后的误差数据。

3.8 实验过程及结果分析

实验首先通过9月2日的48个时刻点的数据预测9月3日48个时刻点的负荷数据。

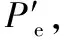
图9 9月3日预测曲线

为了进一步验证本文组合模型的有效性，以同样的方法对测试集中其余日期的数据进行预测，日均误差曲线如图10所示。

图10 三种模型日误差对比

图10中9月4日至5日为双休日，9月7日为美国劳动节。由图9与图10可以看出，SAE-CEEMDAN-BILSTM模型对负荷序列的拟合程度最高，具有很好的预测精度，即使在双休日、劳动节期间该模型的误差率也是最低；SAE-BiLSTM模型以BiLSTM作为误差修正模型也取得了不错的预测精度，但整体上还是比SAE-CEEMDAN-BILSTM模型的预测精度低；而SAE模型由于没有进行误差修正，所以在3种模型中表现最差。取平均绝对百分误差(MAPE)、最大绝对百分误差(Max)和最小绝对百分误差(Min)三种指标进行比较，结果如表2所示。

表2 性能对比(%)

综合上述实验结果，可以得出以下结论：

(1) 由图9、图10可知SAE模型由于没有进行误差修正，所预测精度相对较低，在测试集中平均准确率为93.92%。SAE-BiLSTM模型使用BiLSTM作为误差修正模型，所以预测精度高于SAE模型，测试集中平均准确率为96.52%。而SAE-CEEMDAN-BILSTM模型所使用的误差修正模型可以在不同时间尺度上计算误差序列，提高了预测精度，所以日均准确率在3种模型中最优，测试集中平均准确率达到了97.91%。

(2) 由表2可知，SAE-CEEMDAN-BILSTM模型的三种评价指标均优于其余两种模型，说明该组合模型的预测效果最好；两种组合模型的三种评价指标均优于传统的SAE模型，说明引入误差修正模型能提高模型的预测精度。

(3) 由图10可知，SAE-CEEMDAN-BILSTM模型并不是在每一日的预测精度都达到最优，比如在9月10日其预测精度低于SAE-BiLSTM模型，但从总体上看，SAE-CEEMDAN-BILSTM模型相比其他两种模型具有更好的准确性与稳定性。

4 结 语

本文分析了SAE模型以及CEEMDAN-BILSTM模型的原理，将两种模型进行组合，提出了SAE与CEEMDAN-BILSTM的组合模型，并且将这种组合模型应用到电力系统负荷预测中。经过多次实验以及反复验证，通过对比SAE-BiLSTM模型以及单一的SAE模型可以得出结论：SAE与CEEMDAN-BiLSTM的组合模型应用在电力系统负荷预测具有更好的准确性与稳定性。但随着预测步长的增加，模型的预测精度可能会随之降低，下一步将考虑更多影响负荷序列的因素以增加数据集的特征维度。