应用技术型大学材料力学课程教学改革与实践——以北部湾大学为例

孙 腾 何永玲 鲁 娟＊ 潘宇晨 吴 飞

（北部湾大学机械与船舶海洋工程学院，广西 钦州 535000）

0 引言

材料力学是工程类学科极为重要的一门基础课，是研究材料在各种外力作用下产生的应变、应力、强度、刚度、稳定和导致各种材料破坏的极限。在大学四年的本科教学中，主要涉及的课程包括高等数学、概率统计、材料科学基础以及计算机仿真技术等内容。在我国由制造大国向高端装备转型的大背景下，培养具有坚实力学基础的工程技术人才，对研发高端科技装备的稳定性与可靠性具有重要意义。在材料力学的教学改革过程中，如何提高学生对该课程的学习兴趣，调动学生主动学习的积极性，提高他们的分析问题、解决问题的能力，是应用技术型本科教育亟待解决的重要问题。本文以北部湾大学机械与船舶海洋工程学院的材料力学课程改革为例，详细阐述了材料力学课程中存在的问题和教学改革措施。

1 材料力学课程教学中存在的问题

材料力学课程在教学过程中还是存在着很多问题的。首先，就材料力学课程而言，具有课程涵盖科目广；力学基础概念、公式较多，难以记忆；书本内容抽象，学生理解困难；面对实际工程问题，学生很难应用书本内容对问题简化，建立准确的力学模型。以北部湾大学机械与船舶海洋工程学院的学生为例，在学习材料力学课程授课前，笔者初步统计，还有30%学生在理论力学、材料工程、高等数学等基础课程中挂科，导致后续授课过程中涉及到前面所学习的概念和知识点时，部分原本就未理解的学生学习起来更为困难，进而影响后续内容的深入学习。其次，就任课教师而言，材料力学作为一门传统工科类基础课程，需要应对学科枯燥、学生基础参差不齐、力学理论过于抽象等困难，在教学实践中，教学手段较为单一，通常按照“制订教学计划—利用多媒体讲解教材内容—安排课后作业巩固”的传统模式进行教学，遵循这种标准流程虽然能够按时完成教学任务，却很难做到理论联系实际。此外，对于学生的学习效果的评定也严重依赖平时作业和期末考试分数。除此之外，由于学生数量较多，而专业的材料实验设备较少，导致学生实验动手能力偏弱。最后，就学生而言，虽然能够利用材料力学书本中的计算公式完成教师布置的作业，但并没有对公式进行理解和拓展，导致学生简单地将材料力学课程认为是一门“背公式课程”，严重影响学生在将来的实际工作中，将知识活学活用的能力。综上所述，可将材料力学课程教学中存在的问题归纳为四点：（1）学生基础偏弱，教学内容和教学进程需要调整；（2）教学方式传统，未能迎合时代潮流；（3）实验内容不够丰富，学生动手能力偏弱；（4）评价标准过于单一，缺乏全面完善的考核模式。

2 材料力学教学改革措施

2.1 进一步明确培养人才的目标

2.1.1 应用型人才培养

目前，我国制造业正处在快速发展阶段，急需大量的专业技术人才，而培养这些专业人才的任务主要集中在高校身上。在这些高校中，绝大多数都是以培养应用技术型人才为主。以笔者所在的北部湾大学为例，学校的定位是建设一所高水平的应用技术型大学。在现阶段中国教育的背景下，应用技术型大学是区别于研究型大学以及当前高职院校的一种办学类型。应用型大学培养的学生，动手能力强于研究型，理论基础和专业能力又强于高职院校。在材料力学授课过程中，应侧重三个“用”的能力，即学生的动手测试材料力学行为的能力，面对实际工程问题应用力学原理进行分析的能力和给出最终解决方案的能力。

2.1.2 科研型人才培养

在北部湾大学的施教过程中，虽然绝大多数同学都会进入生产或设计一线岗位，但也有一部分同学希望进一步深造，增强自己的科学研究能力。不同于应用型人才的培养方案，科研型人才的培养则更侧重于“这个公式是如何提出的，公式的计算原理是什么，是否能够根据具体的工况进行改进，并提出新的公式”。同时，在具体的教学过程中，也更侧重于问题的本质，即“为什么会存在这样的问题”“这个问题到底是哪一类问题”“这类问题会产生什么样的结果”。在教学中明确了科研型人才的培养目标，从而合理组织开展教学互动环节，激发他们的创造性思维。

2.2 丰富教学手段

2.2.1 加深基本概念理解、明确公式应用范围

笔者发现，在材料力学的授课过程中，通过将材料力学中的重点概念集中讲解，有利于学生对后续公式的理解。强调公式中各变量的关系及各材料参数的物理意义可以有效加深学生对公式的理解。材料力学中涉及很多复杂公式，以往学生大都是对公式生搬硬套，并不理解实际公式的前提条件和所应用的具体范围。大多数学生往往在考试前通过“连夜突袭”的方式对考试中重点涉及的公式进行记忆，这导致“考完即忘”的不利后果，严重影响后续课程的学习。因此，通过分组讨论公式的具体含义，引导学生独立思考，有利于减少学生对复杂公式的恐惧，对激发学生的创新思维和独立思考能力有着重要作用。在与学生的活动环节中，将布置的课后作业与实际的工程案例相结合，通过“提问+讨论”的方式，将所学的基本概念、计算原理与实际工程中失效零部件相融合。学生在互相提问“是什么原因导致的零部件失效”“涉及了哪些材料力学中的概念”“针对这种工况应选用何种计算公式来评估材料的失效原因”等具有启发式的问题，夯实了材料力学课程所涉及的基本概念，为以后的课程学习打下了坚实的基础。

2.2.2 计算机仿真技术与材料力学相结合

随着计算机仿真技术的飞速发展，利用计算机对实际工程问题进行力学仿真，已成为解决工程实际问题的有效途径之一。常用的力学分析软件如ANAYS，ABAQUS，MATLAB已成为应用较为广泛的有限元分析和数值求解软件。这些软件中兼容了大量的材料力学数学模型，这些模型可以为工程实际生产中，产生的材料失效行为做出预判。在材料力学授课前，可先将本节课涉及到的重点概念与目前当下主流的有限元仿真软件相结合，通过对力学模型的提炼（如图1所示），对简化后的力学模型进行有限元分析，可以得到应力、应变、MISES应力等力学量的分布云图（如图2所示），将复杂抽象的力学量以计算机图形的方式展现给每一位学生。同时，软件的二次开发也为学生提供了一个平台，通过对现有公式的理解，可以将自己提出改进的公式编程，并验证自己的想法是否合理。在材料力学的教学工程中，应充分利用学生对计算机软件的兴趣，合理的利用计算机与网络多媒体资源，将材料力学中的概念可视化、工程化。这极大地提升了学生工程分析能力和科学研究能力。

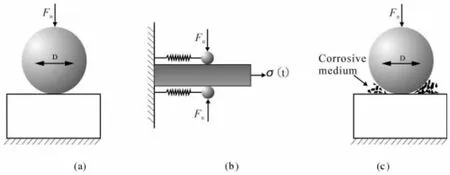
图1 力学模型的简化

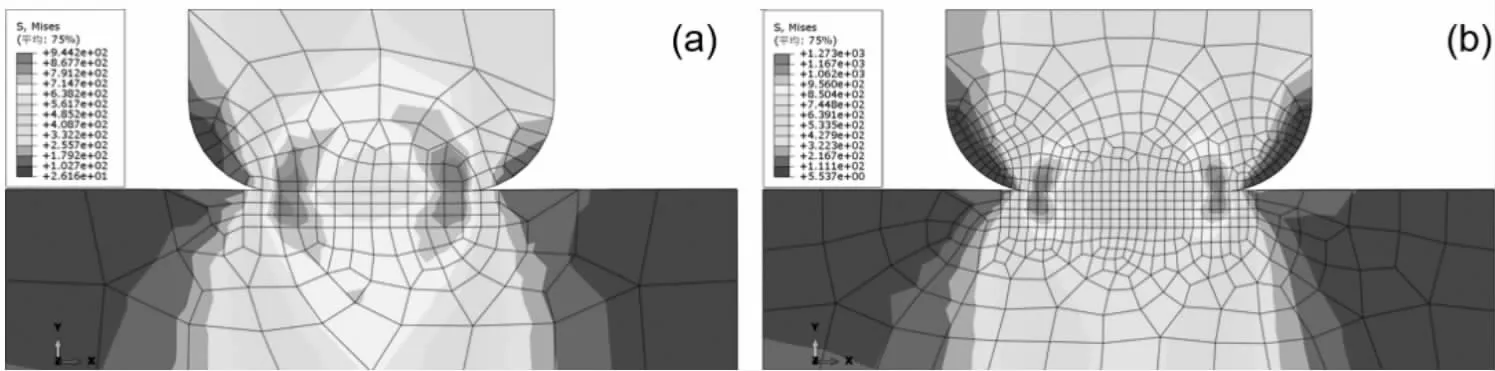
图2 有限元模拟仿真结果-Mises应力云图

2.3 依据材料力学知识，探讨实际工程问题

2.3.1 充分利用中、外数据库进行调研

传统式的以教材为中心的授课模式，很难满足学校对应用技术大学的要求，尤其是以教师为中心的“一言之堂”的授课模式很难培养学生独立思考和创新能力。常见的课堂讨论与分组汇报的模式，虽然能够带动课堂气氛，促使学生主动思考问题，但如何引入一种以实际工程问题为依托的教学模式急需在应用技术大学的课堂上有效展开。对教师而言，在实际备课的过程中，教师可以通过文献查阅，如知网、万方、Web of Science和Elsevier Science等中英文数据库中搜集有关材料力学在实际应用场景中的大量图片来引导学生解决实际问题的能力。对学生而言，学生需要对教师在课堂上提出的工程问题，从材料制造工艺、材料力学、数学建模的角度进行全面阐述，这有利于学生对所学过内容进行全面梳理，也能增强学生对力学、材料、数学、有限元等方面的兴趣与探索欲，由被动接受知识转变为主动学习的良好循环教学模式。

2.3.2 丰富实验内容，提高学生动手能力

在注重工程背景的同时，也需要重视增加材料力学的基本实验，培养学生的动手能力。如材料力学中低碳钢和铸铁试件的力学测试实验，两种不同材料展示出了不同的断裂失效形式。通过让学生比较两种材料的断口形貌，回顾金属工艺学、材料科学基础等相关知识，并提出如何从材料的宏微观角度，解释低碳钢和铸铁试件不同的失效原因。通过矩形截面梁在纯弯曲状态下横截面上的正应力实验，能够观察到梁在纯弯曲时横截面正应力的大小以及分布规律。学生通过材料力学数值估算和有限元软件建模分析，检验计算结果与实验结论是否一致，这一过程很大程度上增强了学生理论联系实际的能力。在动手操控实验设备的过程中，掌握拉伸实验机、材料的疲劳性能测试、扭矩实验、引伸计、电阻应变仪等设备的基本工作原理及使用方法。通过对这些实验设备的使用，有利于培养学生的动手能力，掌握基本的材料性能测试原理，有利于学生奠定坚实的材料力学测试基础。

2.3.3 构建科学、多样化的评价体系

丰富教育教学方式，合理调整考核体系是调动学生积极性的有效手段之一。不同于传统的课程考核形式，笔者将材料力学的教学成果评价体系分为了三大部分：（1）平时成绩分数主要包括学生能够按照自己的理解阐述材料力学中的基本概念。在同学之间的互动环节中，能否从材料力学的角度解释材料及结构失效的原因并举出教材中力学公式的局限性；（2）课后作业包括两部分，一部分是数值理论计算，另一部分是通过有限元计算得出结构的受力云图，并结合有限元的分析结果写出分析报告，详细阐述力学模型的构建、材料力学本构模型的选取以及结构的危险截面的优化方案。（3）笔试在原有考试内容的基础上，增加了实际工程案例论述题。学生需要通过材料力学的原理，从工程案例中提炼出力学模型，阐述结构失效的原因，通过课堂上讲授的材料力学公式，估算出结构关键部位的受力情况。

3 结语

通过以上“明确培养目标+基本概念与计算机仿真技术相融合+针对实际问题提问与讨论+多样化的评价体系”的一套教学流程，可以大幅提高学生对材料力学知识的理解。笔者通过收集实际机械工程零部件失效案例，学生试着通过对零部件实际工况进行力学模型提炼，利用材料力学中的计算公式进行试算并通过有限元分析来解决实际的工程问题。整个过程活跃了学生的课堂气氛，调动了学生的积极性，培养了学生独立思考敢于挑战现有结论并给出合理解释的能力，提高了学生对复杂公式的理解。