基于小尺度网格层析速度反演的孔隙压力预测方法

王智瑞

(中海油田服务股份有限公司 物探事业部，天津 300451)

1 引 言

在油气勘探过程中，地层孔隙压力是油气聚集，分布及运移至关重要的参数之一，孔隙压力的准确预测能够有效提高探井的成功率。在钻井工程当中，泥浆比重以孔隙压力系数作为重要的参考依据，因此能否准确预测地层孔隙压力，直接影响到钻井全程，甚至能够决定钻井的成败。随着勘探目标由浅层向深层扩展，在钻井过程中遇到异常高压的风险事件越来越多，很多石油勘探学者也开始更加重视地层孔隙压力预测方法的开发和利用。

在20世纪初期，已经开始有学者提出异常地层压力是导致井眼垮塌，井漏及井喷等钻井事故的主要因素之一，甚至危及到生命财产安全，但是当时几乎没有相关工作的开展和研究。Hottman等(1965)提出利用地层类比法进行正常压实趋势线的拟合，即著名的等效深度法。该方法适用于构造简单的地层，对于复杂构造地层，例如横向速度剧烈变化的地层，该方法无法进行压力外推反演，从而降低孔隙压力预测的精度[1]。在1968年，Pennebaker等提出利用叠后地震资料来计算地层孔隙压力，该方法在墨西哥湾地区得到了良好的应用效果[2]。Eaton(1975)提出非常著名的伊顿法。该方法利用统计目标工区的已钻井信息来确定伊顿指数，虽然这种方法仍然有一些问题。例如，层速度场无法准确求取；由于测井曲线资料缺失，无法得到准确的正常压实趋势线等。但是这种方法需要的参数较少，所以具有非常高的应用价值[3]。在1980年，Fillippone将钻井资料，地震资料与测井资料联合起来进行应用，提出一种利用单一地层参数计算孔隙压力的方法。该方法无需进行正常压实曲线的求取，进而避免了正常压实速度求取不准带来的误差[4,5]。1987年，Foster等提出利用经验公式建立垂直应力场，进而利用求取的垂直应力反演孔隙压力。该方法在经验公式建立过程当中加入了异常压力成因机制的影响因素分析步骤，进一步提高了压力预测方法的普适性[6]。

刘震(1990)发现地层压力与速度的关系并不是简单的线性关系，利用该理论对Fillippone公式进行了修改，大幅度提高了孔隙压力预测的精度[7，8]。2003年，樊洪海等提出利用层析反演方法优化地震波层速度场模型，进而应用于孔隙压力预测当中，提高了孔隙压力预测精度[9-12]。2018年，徐嘉亮由正常压实情况下的背景速度场出发结合Eaton公式推导了角道集剩余曲率与孔隙压力系数之间的函数关系，消除了层速度参数对压力预测的影响[13,14]。

常规层析成像方法能够对较厚(大于1/4波长)的低速泥岩层进行精确的建模，但是对于(小于1/4波长)厚度较小的泥岩层段，常规层析成像方法的分辨率及精度无法满足速度建模的精度需求。

本文提出针对薄层具有较好反演效果的小尺度网格层析方法进行速度场模型的建立，进而进行孔隙压力预测的策略在渤海A油田得到较好的应用，计算得到的孔隙压力系数与实测压力系数吻合度较高，该方法有望在实际生产当中得到广泛的应用[15-17]。

2 小尺度网格层析层速度建立

目前，异常超压包括多种类型，例如热传导超压，生烃超压，泥岩欠压实超压等。其中泥岩欠压实主导的孔隙压力异常表现为低电阻率、低速的特点。一般情况下，层速度随着埋藏深度的增加而增大，但在部分泥岩层段，由于地层挤压作用，孔隙水不能有效排出，而是保留在泥岩孔隙当中，该部分孔隙水会导致异常高压的产生，而且该层段由于存在地层水而表现为低速的特点[18]。

对于厚度较大的泥岩欠压实地层，常规速度建模方法能够对低速泥岩层段速度进行校正优化。但是当低速泥岩厚度较小时，由于常规层析速度建模方法分辨率的限制，无法准确反演低速泥岩层段的速度，从而导致孔隙压力预测产生较大误差[19,20]。

图1 复杂构造薄泥岩欠压实地层剖面

偏移速度场中，微小的速度扰动都会带来偏移道集动校正量的改变，即

(1)

式(1)中，Δt为i点的到时剩余时差(s)，Δt的大小取决于Δz和Δvi的变化量；Δz为偏移深度与聚焦深度的垂直距离(m)；v表示平均速度(m/s)；Δvi为剩余速度(m/s)；i表示速度模型被网格离散化任意一点；θ为反射角；φ为地层倾角；vi为任意一点的层速度(m/s)。

为使偏移道集同相轴拉平，需要对网格剖面的剖分点速度值进行速度校正，即

(2)

式(2)中，Z′为地层真实深度(m)；Z1为中远偏移距的深度(m)。为了得到真实地层层速度，需要使Δz≈0，即

(3)

式(3)中，v0为初始速度(m/s)；v′为真实速度(m/s)；t0为旅行时(s)。当进行速度校正时，利用式(3)逐点校正网格点的速度值[21]。

本文方法沿用全局速度场迭代优化思路，其具体实现步骤包括：①拾取偏移道集剩余曲率；②利用拾取的剩余曲率建立剩余旅行时矩阵；③采用共轭梯度算法求解剩余旅行时矩阵，得到剩余速度体；④利用HRS软件对叠前及叠后地震数据进行扫描，以提取地层倾角及方位角；⑤利用剩余速度体修正速度场模型，完成一次速度校正；⑥重复①至④步骤，通过偏移道集是否存在剩余曲率作为迭代是否终止的判别依据。利用网格层析速度建模方法进行孔隙压力预测流程图如图2所示。

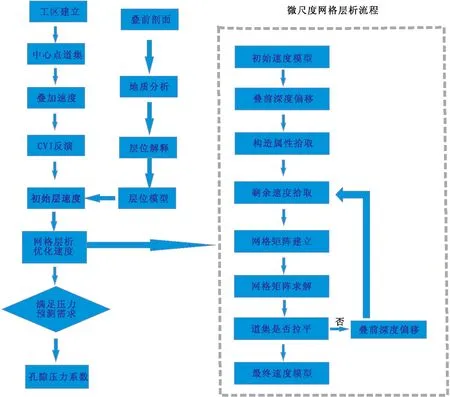
图2 孔隙压力预测流程

3 目标实际数据应用

A油田存在多发欠压实薄泥岩层段，如图3所示，该区存在高压甚至是超高压风险，为后续钻井带来非常不利的影响。

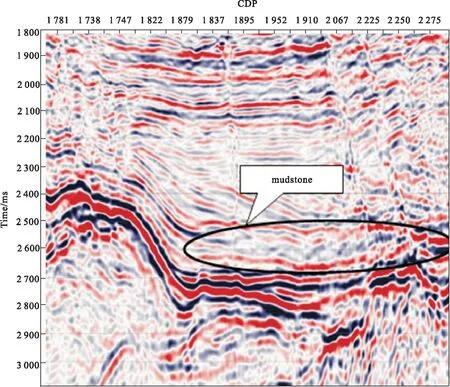
图3 薄泥岩欠压实地层

分别利用常规层析方法和小尺度网格层析速度建模方法进行三维速度场模型的建立，本文采用10 m×10 m的网格步长进行网格剖分，并且抽取1井Inline线进行方法对比，如图4所示。常规层析方法由于速度场分辨率低，对于小于1/4波长厚度的地层没有响应，所以无法对泥岩欠压实低速层进行速度校正，利用该速度模型进行孔隙压力预测显然是不正确的。利用本文提出的小尺度网格层析方法进行速度建模能够对小于1/4波长的低速层进行精确的速度校正，进而提高速度场建模精度及压力预测精度。

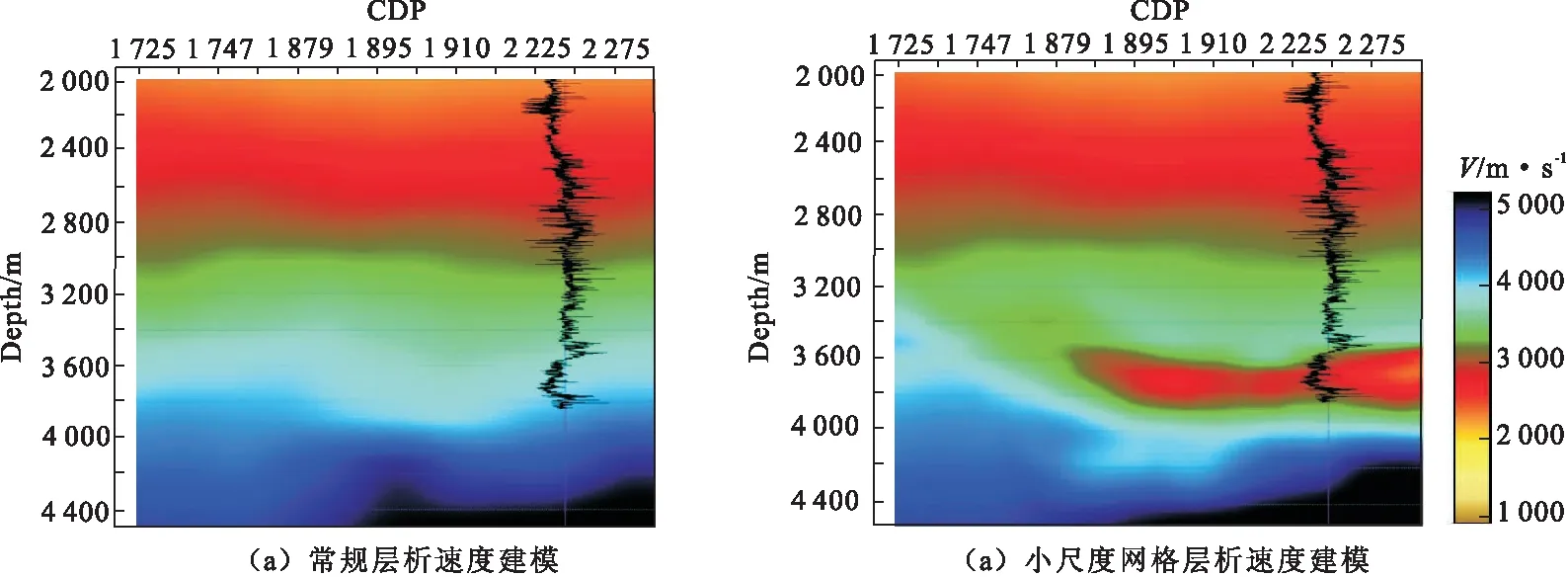
图4 速度模型

图5所示为抽取的单道速度曲线与实钻井声波速度曲线的比较。常规层析成像方法建立的速度在中浅层与声波速度吻合程度较高，在泥岩欠压实层段存在较大的误差。小尺度网格层析速度建模方法建立的速度模型与声波速度在浅中深层段吻合程度均较高，从而说明本文方法对于低速泥岩速度场建模更为适用。

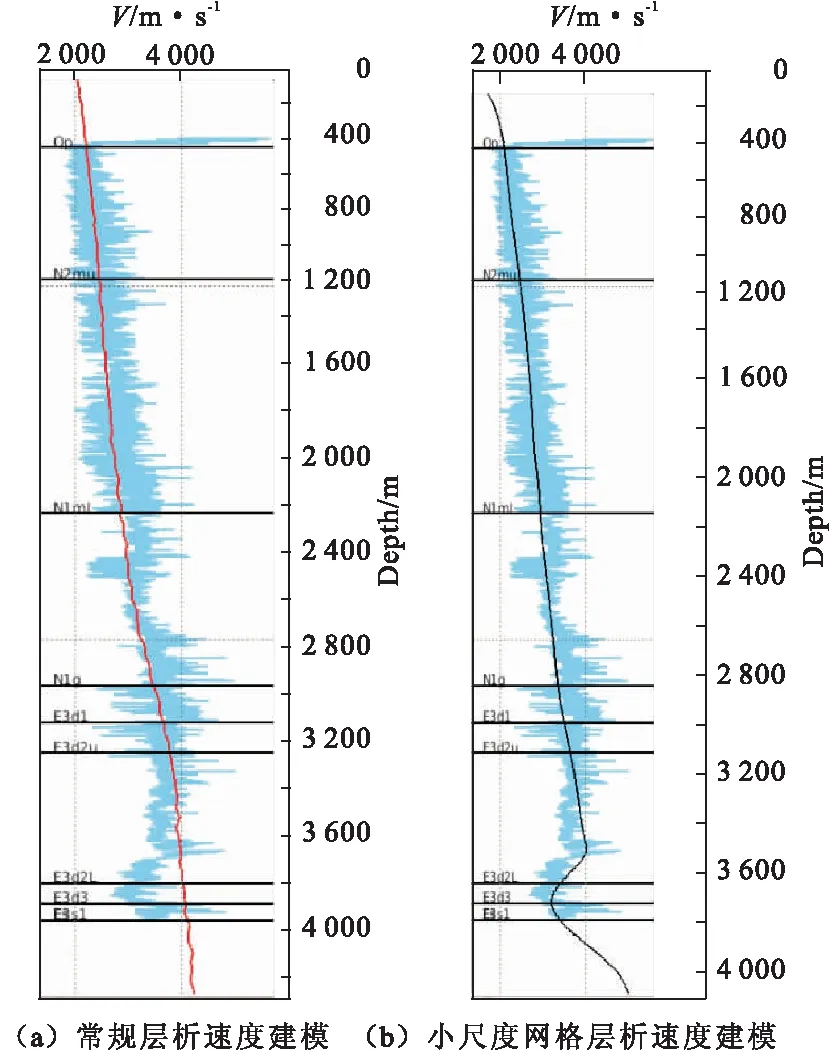
图5 速度曲线

孔隙压力系数为真实地层实测压力与正常压实情况下的压力比值，它用来表征地层压力的异常情况。分别应用图4所示的速度场进行孔隙压力系数计算，预测结果如图6所示。常规方法计算得到的孔隙压力系数与实测压力系数值吻合度较差，误差为0.3 P/Mpa，利用本文方法预测的孔隙压力系数与实测压力系数吻合程度较好，误差仅为0.01 P/Mpa。

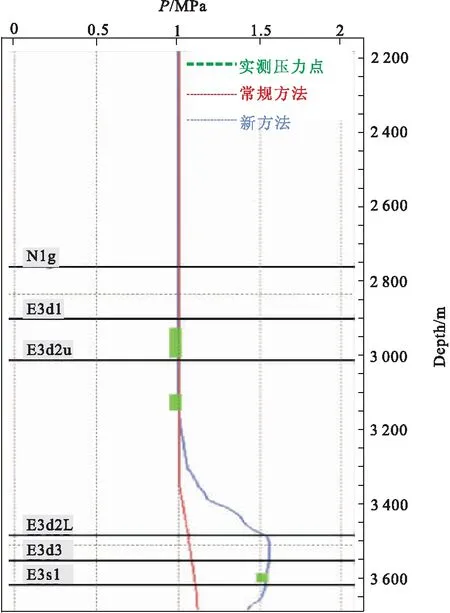
图6 实测压力系数与本文方法测量结果比较

4 结 论

常规层析成像方法能够对初始层速度模型进行速度校正，以得到更为精准的层速度，但是该方法受地震资料品质的限制，其精度及分辨率均难以得到有效保障。本文针对渤海A油田中深层广泛发育低速泥岩，且存在较大超高压风险的实际情况，提出利用小尺度网格层析成像方法进行速度场模型建立，进而计算孔隙压力值。由本文方法与常规方法比较中可得出以下结论：

1)常规层速度建模方法对于地震资料品质的依赖程度较高，且对于小尺度构造或较薄地层无法获得准确速度场，小尺度网格层析速度建模方法针对局部构造进行网络剖分，通过校正网格点速度值以优化速度场模型，该方法对于目标层位的速度优化更为适用，且精度更高。

2)小尺度网格层析方法计算效率由网格步长大小决定，减小网格步长能够提高速度反演精度，但是同时降低了计算效率；相反，增大网格步长能够提高计算效率，但计算精度有所下降。

3)层析成像方法对于地震资料品质的依赖程度较高，应用低信噪比和低分辨率的地震数据无法获得高精度的速度场模型。所以在进行本文方法前，应对叠前数据进行去噪处理，以满足层析速度建模需求。