基于深度学习的地面拖曳式瞬变电磁快速成像方法

冼锦炽，蔡红柱,2，熊咏春，何子昂, 胡祥云,2

(1.中国地质大学 地球物理与空间信息学院，湖北 武汉 430074;2.中国地质大学 地质过程与矿产资源国家重点实验室，湖北 武汉 430074)

1 引 言

瞬变电磁法(Transient Electromagnetic Method, TEM)作为一种有效的地球物理观测方法，被大量应用于矿产勘查[1-3]、水文地质调查[4, 5]、工程地质勘探[6-8]等领域中。该方法利用激励源向地下发射一次脉冲磁场，通过观测由地下介质产生的随时间变化的二次场，获取地下电导率分布信息。

由于瞬变电磁法采集方式灵活，探测装置可以搭载于各类快速移动平台上，主要方法包括采用直升机、固定翼的航空瞬变电磁(Airborne TEM)[9, 10]，采用无人飞艇，无人机作为载体的半航空瞬变电磁(Semi-airborne TEM)[11, 12]以及由陆地车辆牵引的地面拖曳式瞬变电磁(Ground-based towed TEM, tTEM)等[13]。上述方法使瞬变电磁法可以适用于不同的应用场景，克服复杂地形的限制，从而实现大规模数据的高效采集。在实际应用中，航空瞬变电磁与半航空瞬变电磁测线距离一般在200 m以上，使得横向分辨率有所限制。此外，较高的仪器设备调动成本也制约了航空与半航空瞬变电磁的应用。相较于航空与半航空瞬变电磁观测系统，地面拖曳式瞬变电磁装置在浅地表0～70 m范围内具有更高的分辨率，而且相较于空中飞行的观测方式，需要校正的误差源更少，数据信噪比更高[13]。传统地面电磁探测方法,如直流电法[14]和回线源瞬变电磁法[15]，虽然也可以在浅地表提供可观的勘探分辨率，但设备移动速度慢，数据采集效率较低，很难满足大区域地质调查的需求。地面拖曳式瞬变电磁法弥补了传统地面电磁方法的部分缺点，结合牵引车辆装配的高效收发装置，可以快速获取大区域浅层地下信息。

地面拖曳式瞬变电磁装置测量灵活，工作效率较高，在相对平坦的地形进行数据采集，一天工作量能覆盖数十公顷范围[16]。由于该方法在时间和空间上的高密度采样会产生大量的数据，三维瞬变电磁反演需要付出高额的计算成本，因此常采用一维反演方法对地下空间进行电阻率成像。传统一维反演技术通过迭代求解，最小化正演数据与观测数据之差的目标函数，从而反演获得地下层状电阻率模型[17, 18]。但地球物理反演问题往往是非线性的，线性迭代反演方法依赖于初始模型与正则化参数的选择，容易陷入局部最小值中而无法收敛至全局最小值[19]。因此，一些完全非线性算法被引入到瞬变电磁反演中，包括模拟退火法[20, 21]，粒子群优化算法[22]，跨维贝叶斯算法[23]等。非线性反演算法能有效结合先验信息，避免反演问题线性化，但随着模型空间的增加，反演参数会呈现指数性的增长，导致计算成本大幅升高，难以解决大规模数据处理的问题。

随着硬件计算能力的发展，基于神经网络的深度学习技术在图像处理，自然语言处理等多个领域中实现了大规模的商业应用，也逐渐引入到地球物理领域中，其应用场景包括勘探地震数据反演与解释[24-26]，重磁数据反演成像[27, 28]，电磁数据反演[29, 30]。在瞬变电磁反演应用上，Li等[31](2020)通过卷积神经网络与长短记忆层组合的网络架构实现了考虑飞行高度的航空瞬变电磁一维快速成像。Wu等[32](2021)利用卷积神经网络方法对航空电磁数据进行了反演。Bang 等(2021)[33]基于循环神经网络技术对多条测线的航空电磁数据进行了二维电阻率成像。目前深度学习方法在航空瞬变电磁中应用较多，但在地面拖曳式瞬变电磁法应用上尚未有深入的研究。

本文基于卷积神经网络与双向长短期记忆网络的深度学习框架，开发了面向地面拖曳式瞬变电磁系统的快速成像方法。通过B样条插值方式来描述地下电阻率的变化，生成用于网络训练的数据集。在网络训练的损失函数中引入光滑约束与灵敏度加权，增强网络反演对浅层电阻率的识别能力，避免反演出虚假异常。通过测试理论模型验证了算法的可靠性与鲁棒性，证明本文开发的算法可以快速处理大规模的地面拖曳式瞬变电磁数据，并保证反演的准确度。

2 地面拖曳式瞬变电磁法

地面拖曳式瞬变电磁法最早由丹麦Aarhus大学于2000年提出，到2019年逐步发展为成熟的商用瞬变电磁法系统，并在丹麦国家地下水调查项目中得到大规模的应用[13]。地面拖曳式瞬变电磁牵引车辆携带供电装置，拖曳带底座的水平发射线圈与接收线圈。装置的发射线圈大小为2 m×4 m，接收线圈大小为0.56 m×0.56 m，两个线圈中心的偏移距为9 m，如图1所示。线圈搭载于非金属材质的滑橇上，滑橇在地面上滑动引发线圈振动所产生的噪声可以通过系统滤波以及高重复频率的发射电流消除。牵引车辆一般以15～20 km/h的速度行驶，并采集数据，测点位置通过安装在发射线圈与接收线圈的GPS进行记录。类似航空瞬变电磁法，地面拖曳式瞬变电磁法一般采用双发射机产生激励电流。低发射磁矩(Low Moment)的发射电流为2.8 A，避免接收装置由于过大的一次场达到饱和而无法接收二次场信号。高发射磁矩(High Moment)的发射电流为30 A，从而获得更大的勘探深度。低发射磁矩接收的时间道一般为4～15个，对应早期数据，高发射磁矩接收的时间道一般为14～23个，对应晚期数据。双发射机的设计可以使勘探深度达到地下80 m附近。为保证勘探的分辨率，行驶速度最好限制在10～20 km/h，沿测线方向的测点距离在2～10 m。

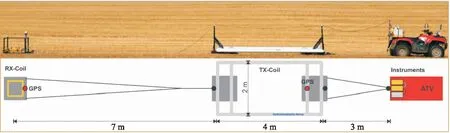
图1 地面拖曳式瞬变电磁装置示意图[13]

对于搭载在快速移动平台的瞬变电磁系统，在正演时必须考虑其完整的系统效应来减少误差源对数据的影响。主要的系统响应因素包括发射电流波形，时间门宽度，接收装置的低通滤波效应，发射线圈与接收线圈高度等。

3 基于深度学习的反演方法

3.1 网络结构

本文所采用的深度学习方法主要包括卷积神经网络(Convolutional Neural Network, CNN)与双向长短时记忆网络(Bi-directional Long Short-term Memory, Bi-LSTM)。将二者组合搭建的网络框架“喂入”数据集训练网络，使其可以直接表达电磁数据输入与电阻率模型输出之间的映射关系。在“端到端”思想的指导下，训练好的网络可以被用于快速实现地面拖曳式瞬变电磁的一维反演。

CNN与LSTM在处理时序数据上有独特的优势[34]，CNN-LSTM组合网络框架能很好地适用于按时间顺序采样的瞬变电磁数据。CNN-LSTM框架主要由卷积层(Convolution Layer)，LSTM层与全连接层(Dense Layer)组成，下面将简述卷积层与LSTM层的具体操作。

卷积层的核心作用是对输入的时序数据进行卷积操作，提取输入数据的特征，其数学形式表达如下：

(1)

LSTM层附加于卷积层之后，用于学习卷积层提取特征中重要的时序信息。LSTM结构主要包含遗忘门ft，输入门gt，输出门qt，以及状态单元ct。通过三个门组成的系统控制信息流动，可以不断更新每个独立的状态单元，学习不同时步上的数值关系。在门计算完毕后，状态单元将整合各个门所包含的信息，更新状态单元ct，再通过输出门获得单个LSTM单元的输出。每个时步t更新过程如公式(2)～公式(6)所示：

其中，∘为哈达玛积(Hadamard Product);b为对应门的偏置项;U为对应门的循环权重;W为对应门的输入权重;xt为输入向量在t时步上的值;yt为t时步的输出;σs为sigmoid激活函数;σa为tanh激活函数。传统的LSTM只考虑了t时步之前的信息，而Bi-LSTM能同时获取t时步前后的信息。Bi-LSTM模块首先将输入序列正序输入，再将输入序列倒序输入，再对Bi-LSTM单元进行更新与输出。理论上，电磁反演成像需要同时考虑早期与晚期瞬变电磁响应，Bi-LSTM层处理更符合实际反演所表达的物理规律。

本文采用的网络框架如图2所示，网络结构由3个用于特征提取的卷积层、1个Bi-LSTM层以及2个全连接层组成。卷积层的卷积核大小为(2×1)，卷积核移动步长为1，卷积核个数为256。每个卷积层之间由激活函数连接，激活函数为ReLU函数[35]。通过卷积层提取的数据特征被输入到Bi-LSTM层中，Bi-LSTM层的输出则进一步作为全连接层的输入。全连接层总共2层，每层有512个神经元，随机失活(Dropout)比例为0.2。随机失活是在网络训练中的一种有效的正则化策略，随机使选中神经元的输出为0，减弱神经元之间的依赖性，防止网络训练过拟合。全连接层(包括输出层)也附加了ReLU激活函数层，使网络输出的对数电阻率不会小于0。

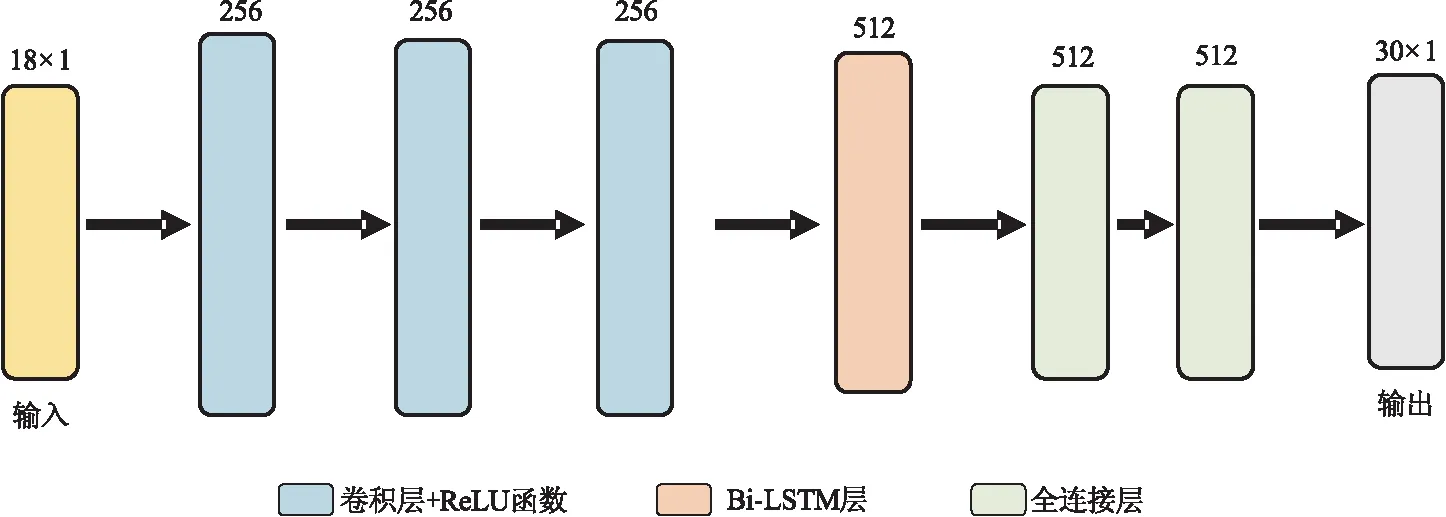
图2 网络框架示意图

3.2 训练集生成

考虑地面拖曳式瞬变电磁装置的主要探测范围集中于浅地表，在这个深度范围上多为较连续分布的第四纪覆盖层，一般采用光滑反演方法进行处理[36]。基于上述经验，本文基于B样条插值构建了相对光滑且纵向连续的层状电阻率模型，如图3所示。首先设定反演深度为120 m，然后确定6个控制点，控制点对应的x坐标为电阻率，y坐标为深度。所有控制点的电阻率在5～500 Ω·m范围内进行超立方采样，2个控制点的深度分别固定在0 m与130 m处，其余4个控制点的深度随机确定，但控制点之间的间隔不小于10 m。在确定好控制点之后，将模型按对数递增的方式剖分为30层，依据6个控制点使用B样条插值对层状模型插值，可产生含30个电阻率且固定层厚的模型。

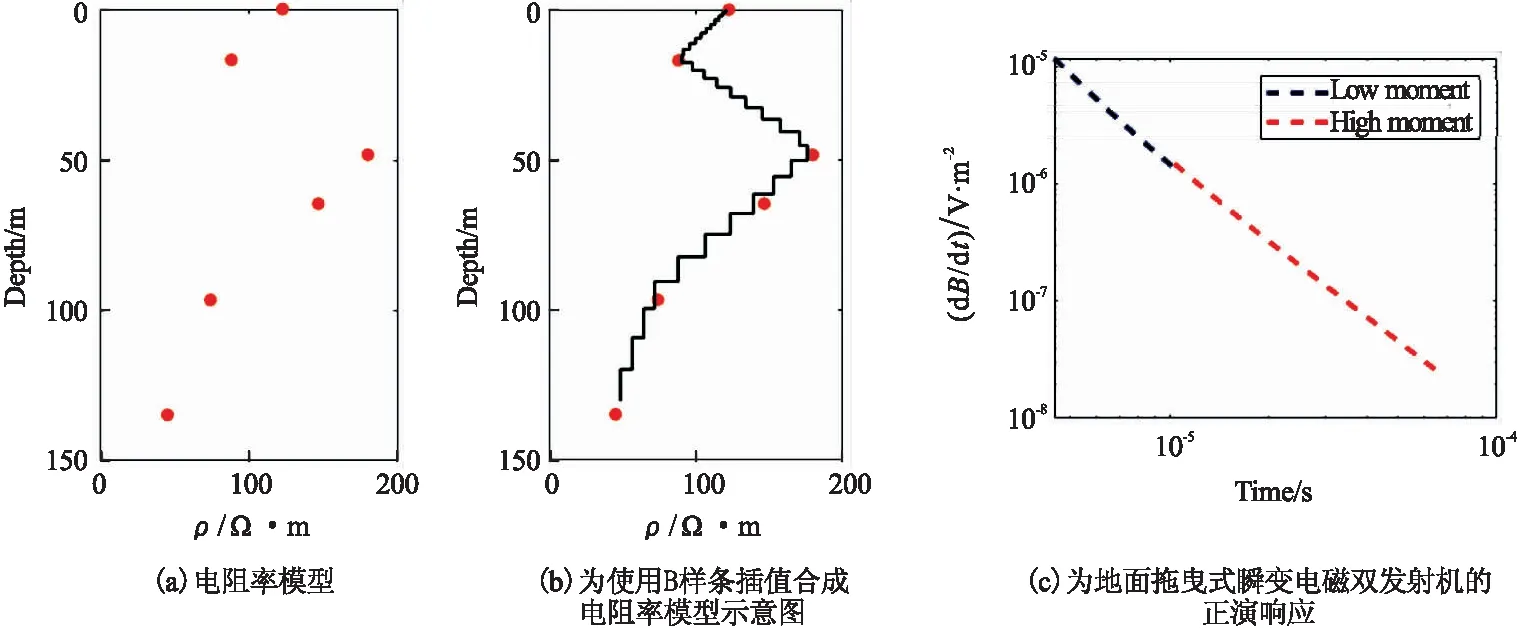
图3 训练集样本生成示意图

在获得相应模型后，采用Auken等人[37]提出的算法正演计算电磁响应。由于发射系统采用双发射机采集序列来分别获取瞬变电磁法的早期与晚期时刻的数据，正演时需要分别考虑两个发射机的发射波形，时间门宽度，接收装置的低通滤波效应，前门效应。低发射磁矩对应的接收时间道为4个，高发射磁矩对应的接收时间道为14个。本文将两次正演响应dBz/dt拼接为单个18×1向量作为网络输入，30层电阻率的一维模型作为网络输出，确定电磁响应-电阻率的数据-标签关系。正演算法基于OpenMP并行计算，单个样本计算时间为0.24 s。

3.3 损失函数

神经网络的基本思想是通过网络来构建输入与输出之间的映射关系。网络输入为瞬变电磁数据d，网络输出为电阻率模型m，则映射关系可以表示为：

m=F(d;θ)

(7)

其中,θ为网络参数;函数F表示电阻率模型m与瞬变电磁数据d的映射关系。网络通过训练学习，可以获得表征高度非线性函数F的能力。网络的训练本质上是最优化问题，目标是使损失函数最小化。损失函数常定义为数据标签与网络预测值之间的平均绝对误差：

(8)

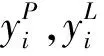
基于DOI理论，一维电阻率模型的雅克比矩阵计算如下：

(9)

其中,Jij表示第j个模型参数mj对第i个数据响应的灵敏度，归一化对应数据点上的噪声Δdi并对矩阵J进行列方向的求和：

(10)

其中,sj为对应层电阻率的累加灵敏度。对sj做归一化处理后，将其作为损失函数的约束项。

在传统电磁反演方法中，常采用基于最小偏差模型约束或最大光滑稳定泛函的平滑反演方法，在反演中施加光滑约束可以有效解决反演的多解性与不稳定性问题[39]。基于B样条插值的样本生成方法使电阻率深度上更连续，因此加入光滑约束可以避免相邻层电阻率的突变，并使网络训练更稳定。将网络预测的各层电阻率值进行错位相减，取其平均相对误差作为光滑约束项：

(11)

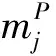
(12)

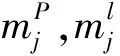
4 理论模型研究

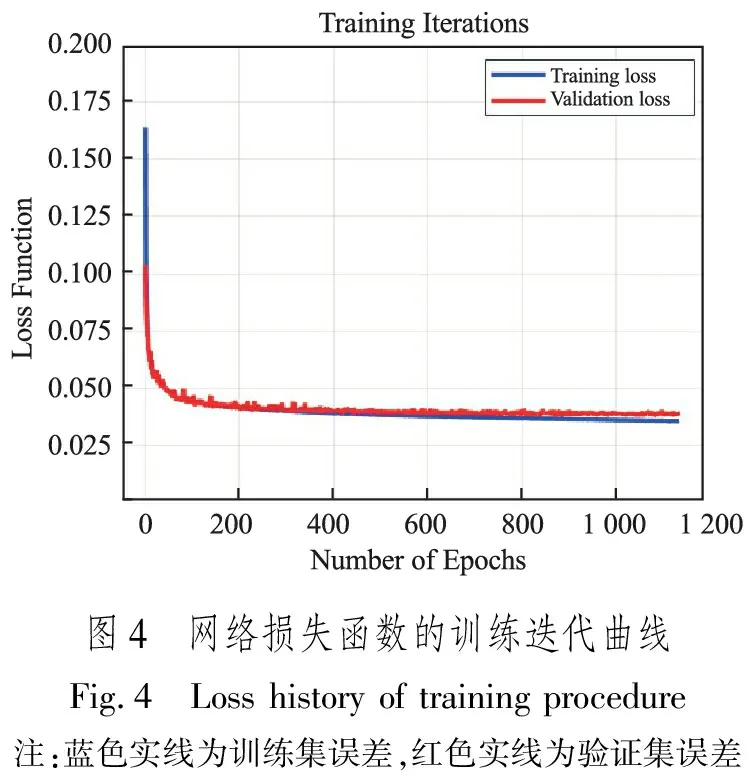
按照前文所述的数据集产生方法，初始训练样本集为10万个，按7∶1.5∶1.5将数据集划分为训练集，验证集，测试集。算法基于开源代码库tensorflow2.1实现，在搭载GTX 1080Ti的工作站上训练时间为2.5小时。图4展示了网络训练损失函数随网络迭代次数的变化，根据早停策略，本文选择在第1 150次迭代后更新的模型作为网络训练的最终结果。为了验证算法的有效性，在测试集和多个典型的地电模型上进行了反演测试。

4.1 算法鲁棒性分析

在对测试集的评价中，本文向测试集的数据加入了3%的随机噪声，以测试算法的鲁棒性。通过以下方式来评价测试集中的模型误差与数据误差：

(13)

式中，upred为网络的预测值;ulabel为测试集的数据标签。

通过对测试集进行误差分析，绘制了反演结果的模型拟合差和数据拟合差的关系分布。图5(a)为测试集反演结果对应的模型误差与数据误差交会图，图5(b)～图5(e)为4个随机从测试集中挑选的反演结果。如图5(a)所示，网络预测结果对应的数据拟合差基本都在10 %以内，绝大部分数据拟合差低于5 %。而由于一维电阻率模型存在较多的等效模型，可以发现即使在测试集中的模型拟合差较大，但其正演的电磁数据拟合差仍相对较小。图5(b)～图5(d)展示了部分测试集样本的反演结果，图示表明数据噪声主要对深部电阻率的影响较大，对浅层电阻率的影响较小。由于瞬变电磁法的勘探分辨率会随着地下深度的增加而下降，算法反演结果基本符合电磁勘探规律。

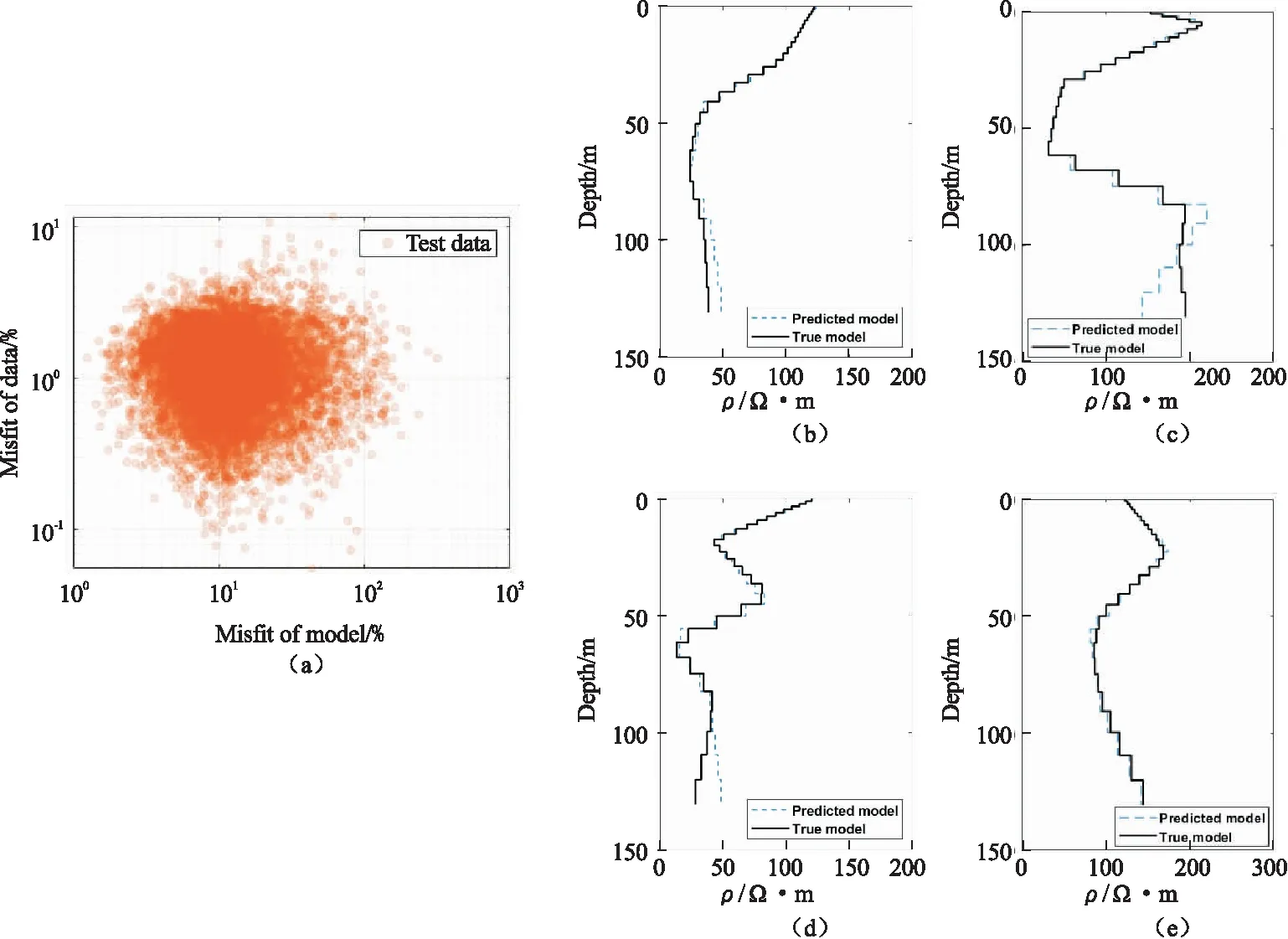
图5 测试集模型误差与数据误差分布

4.2 层状理论模型测试

由于测试集的样本生成方式与训练集相同，网络的泛化能力往往可以覆盖与其有着相似分布的数据[36]，为了进一步验证网络的反演能力，需要测试有别于当前模型生成方式的样本。图6(a)～图6(d)分别为典型的四层电阻率模型，其电阻率并不具备类似训练集中的纵向连续性。在模型测试时，均在电磁响应数据中加入了1 %的随机噪声。对于图6(a)和图6(b)的模型，反演结果可以较好地描述电阻率模型逐渐递减或逐渐递增的形态。对于图6(c)和图6(d)的模型，反演结果能较清晰地区分主要层位电阻率分布，反映模型的高阻层与低阻层。图6展示了上述4个模型的正演电磁响应曲线和实际电磁响应曲线的拟合结果，电磁响应曲线拟合差较小。由于在模型产生时，采用较密的层数来离散一维空间，基于B样条插值的方法也使层位电阻率变化更连续。因此反演结果在电阻率突变界面上表现得更为光滑，层与层的分界并不足够明显。虽然反演结果相对光滑，但在实际反演解释中，光滑模型仍可以根据经验有效地确认实际的电阻率层位。

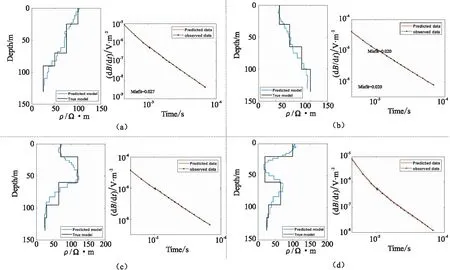
图6 不同理论模型的测试结果

为了进一步验证网络反演算法的可靠性，本文在层电阻率变化更大的理论模型上进行了反演测试，对比了CNN-LSTM反演方法和传统Marquart反演结果。理论模型参数如表1所示，所测试模型的正演数据中均加入了1 %的随机噪声。Marquart反演方法的初始模型设置为100 Ω·m，模型层数为30层。如图7所示，在模型A的测试上，电阻率界面的突变可以很好地在网络反演结果中得到体现。高阻夹层的实际电阻率为120 Ω·m，CNN-LSTM算法对高阻夹层反演结果约为135 Ω·m，Marquart算法反演结果则大于150 Ω·m，CNN-LSTM算法结果更准确。如图8所示，在模型B的测试上，Marquart反演算法在浅部地表产生了高阻畸变，反演结果的低阻夹层厚度要远大于真实模型。CNN-LSTM算法可以较准确地反演模型的低阻夹层的电阻率与层厚度，深部电阻率信息也基本与真实模型一致。从模型A, B的Marquart算法反演结果可以看出，其反演结果容易在浅部产生部分电阻率突变，深部信息基本依赖于初始模型。CNN-LSTM算法在浅地表的反演结果则相对稳定，整体符合真实模型的电阻率变化。在浅部可以较清晰地体现层电阻率的突变界面。在80 m以下，由于对一维空间采用对数递增的层模型形式进行剖分，深部剖分的层厚度较大，电阻率信息只能体现真实模型的形态变化，很难准确表现深部的突变界面。

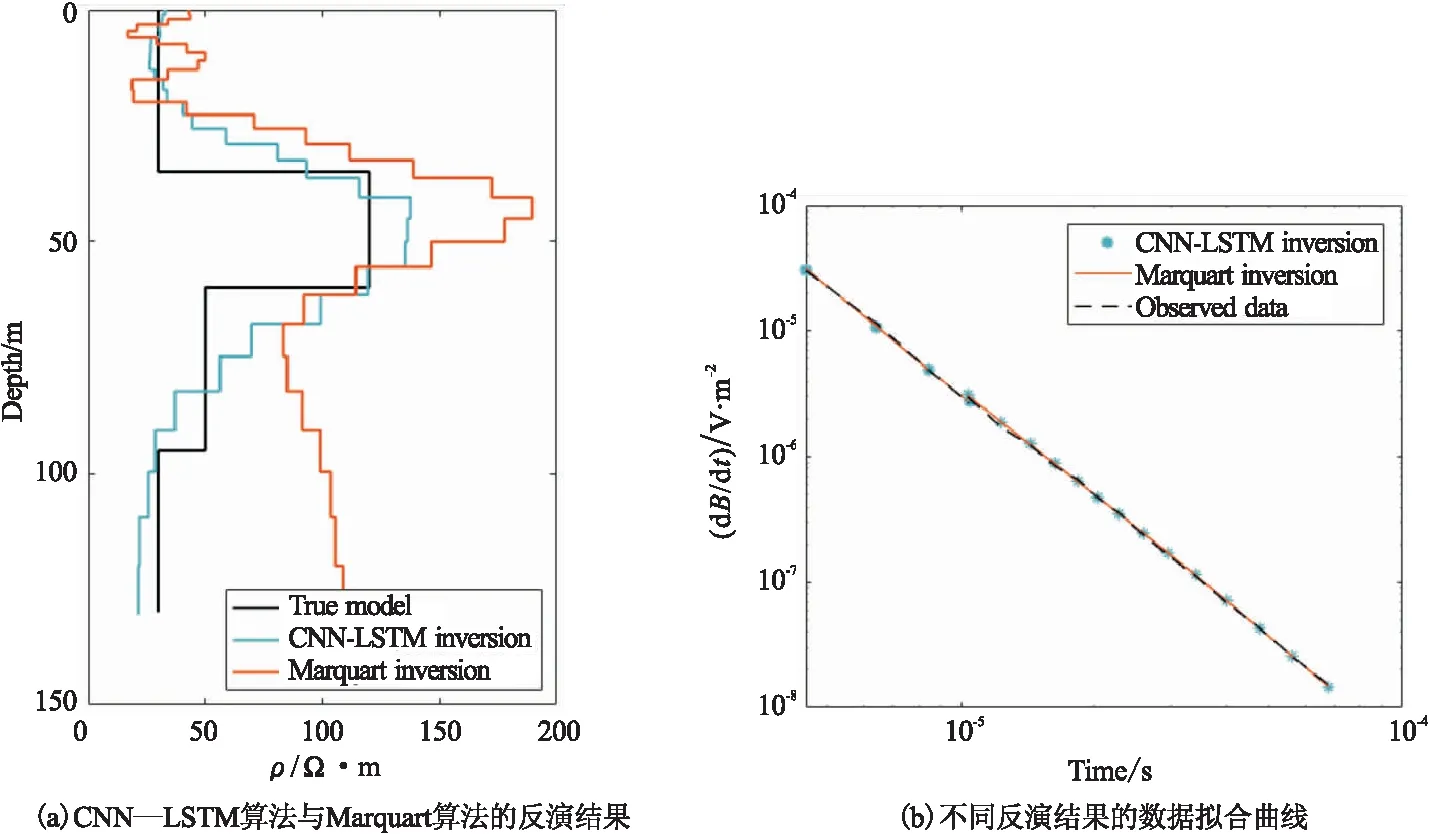
图7 CNN-LSTM算法与Marquart算法对模型A反演结果的对比

表1 理论模型A和B的参数设置

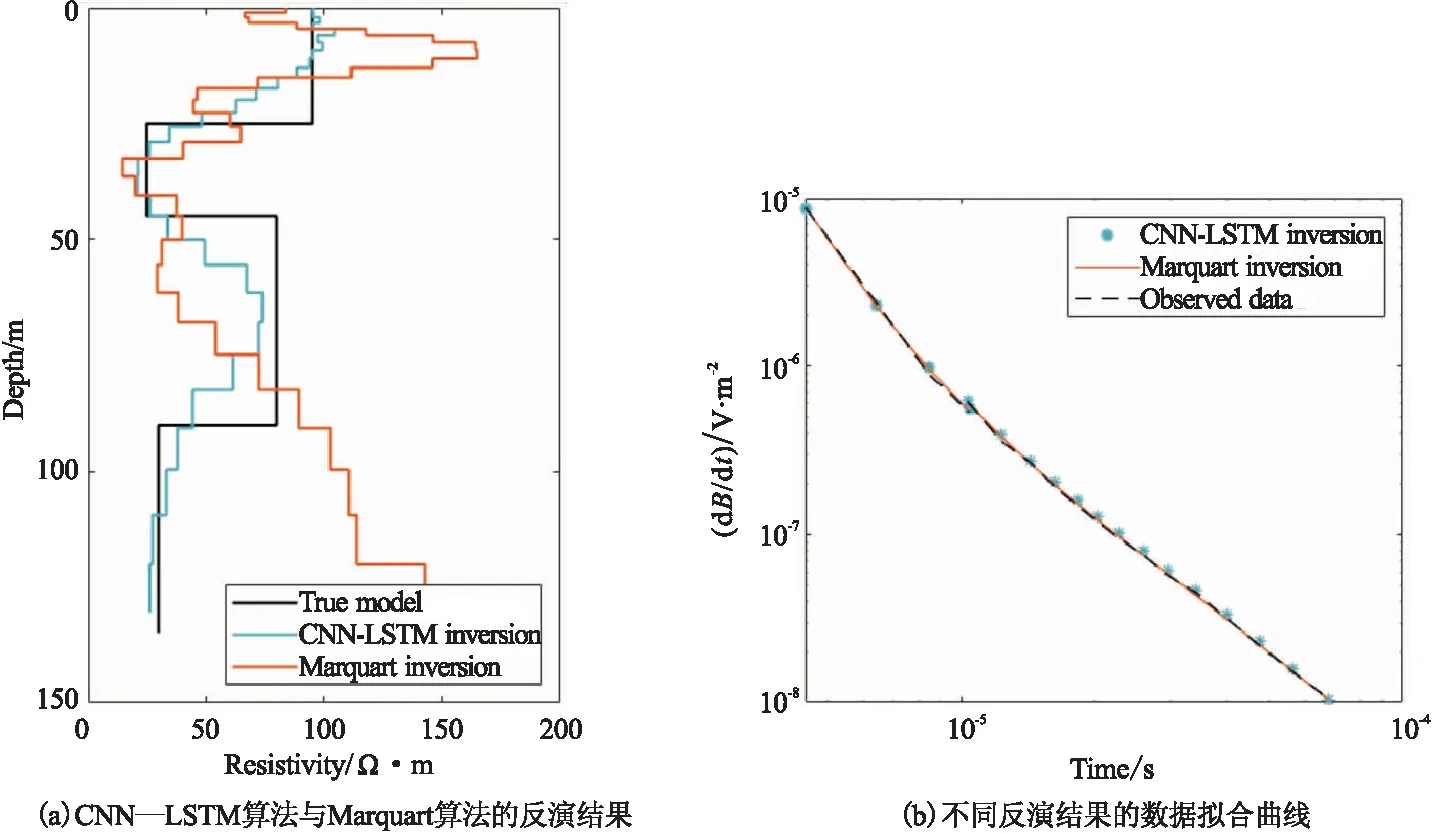
图8 CNN-LSTM算法与Marquart算法对模型B反演结果的对比

本文进一步分析了两种方法的反演时间。基于Fortran实现的Marquart算法，反演模型A迭代次数为10次，反演耗时7.21 s，反演模型B迭代次数为12次，反演耗时8.56 s。Marquart反演方法由于需要对每个数据都迭代求解雅克比矩阵，对于大规模数据处理，其处理时间将以倍数增加。而基于CNN-LSTM网络的反演算法在网络完成训练后，无需迭代即可投入反演，反演单个模型时间为0.04 s。相较于传统Marquart算法，所开发的反演算法不依赖于初始模型，可以避免陷入局部极小值，并且具备更快的反演速度。

5 结 论

本文基于数据驱动的深度学习方法，结合卷积神经网络与长短期记忆神经网络技术，提出了针对地面拖曳式瞬变电磁法的快速反演成像方法。本文采用B样条插值方式构建了一维层状样本数据集。通过在网络训练的损失函数中引入灵敏度加权与光滑约束，使网络对浅层电阻率反演结果更准确与稳定。上述方法也使网络学习到的电阻率模型特征更光滑，反演结果也贴近于传统光滑反演方法所产生的结果，所恢复的突变的电阻率边界较为模糊，不够聚焦。理论模型反演结果表明,基于CNN-LSTM网络的反演方法具备更快的速度，对浅部地层电阻率的反演结果更稳定。因此，本文所提出的算法适用于大规模地面拖曳式瞬变电磁数据反演快速成像，并在实时数据成像具备广阔的应用前景。