含逆变型分布式电源的配电网故障暂态分析

魏亚军，李开灿，董 振

(国网山东省电力公司济宁供电公司，山东 济宁 272000)

分布式发电技术的发展使得越来越多的分布式电源(distributed generator, DG)并入配电网并向电网供电。然而大量分布式电源接入到配电网后，给配电网的故障诊断带来了诸多不利的影响，分布式电源的接入改变了配电网的运行状态。分布式电源既可以对外供电，也可以在电网电能充足时进行充电储能，这就使得配电网潮流具有双向性。由于风电、光伏等一次能源的出力具有较大随机性，导致配电网潮流也具有较大随机性，从而改变配电网的调度和控制。

为促进分布式电源与配电网的互连，国家已经制定相关的标准[1-2]，规范分布式电源对电网运行的影响评估，特别关注对馈线负荷供电占10%以上的分布式电源[3-4]。当电网发生故障时，分布式电源产生的电流可能对配电网馈线的保护产生较大影响[5-7]。大规模的分布式电源可以改变短路电流大小，引起保护装置误动。故障电流受分布式电源影响，也可能使重合闸安装处的电流超过其最大开断电流极限，影响其动稳定性和热稳定性[8]。故障电流也会影响熔断器动作，使其提前熔断，进而导致重合闸熔丝失配，大大影响馈线的可靠性[9]。

为解决上述问题，在传统故障分析方法的基础上，首先，本文针对含逆变型分布式电源的配电网建立故障分析模型以评估分布式电源在次暂态(故障后第1周期)和暂态(3～10周期)期间对故障的影响；然后，提出新型配电网故障分析方法，能够准确计算来自分布式电源的故障电流和电网检测的电流的均方根值；最后，通过IEEE标准配电网上的算例分析，证明该方法在不同故障情况下计算故障电流的准确性。

1 含IIDG的配电网故障计算模型

在传统的配电网中，变电站是唯一的电源。由于变电站通常远离大型发电机组，在配电网发生故障时，系统很难检测出故障电流初始的次暂态分量，因此，故障电流通常由稳态值来近似[10]。如图1所示，ES为变电站通过戴维南定理等效为电压源，ZS是系统阻抗，Z11、Z12分别为线路L1和L2的阻抗，线路的正负序阻抗相等，其零序阻抗分别为3Z11和3Z12，ZT为变压器阻抗。在序电压和序电流的边界条件约束下，图1中节点3发生单相接地故障时的复合序网络如图2所示。

图1 含IIDG的配电网系统Figure 1 A distribution network with IIDG

图2中，IIDG的端电压可以表示为

图2 当节点3发生单相接地短路故障时的复合序网络Figure 2 A compound sequence network when a single-phase short-to-ground fault occurs at node 3

(1)

(2)

其中，ZΣ0=ZT(ZS+3ZL1)/(ZS+3ZL1+ZT)+3ZL2。IIDG的输出电流与端电压可以描述为

(3)

由于IIDG的输出电流与端电压之间存在非线性耦合关系，而该耦合关系依赖于IIDG的电流控制策略，因此需要采用迭代法来求解该约束[11]。首先，假设IIDG形成孤岛得到故障后的初始端电压；然后，根据IIDG的初始电压和电流控制策略，得到短路电流的序分量；最后，将其代入式(1)、(2)来更新终端电压直到收敛。

逆变型分布式电源的输出暂态特性主要取决于控制器，目前主要控制方式采用双闭环控制策略。逆变型分布式电源的双闭环控制原理如图3所示，分为电流内环和电压外环，均采用PI控制器。内环用于控制电流，外环调节功率输出。在双闭环控制策略中，控制器通过调节分布式电源输出端电压的幅值和相位，来控制有功和无功功率输出，并快速为内环电流控制提供电流基准值[12]。目前常用的控制系统中，通常只考虑IIDG电压正序分量作参考，同时消除负序分量，将IIDG等值为正序电源模型。

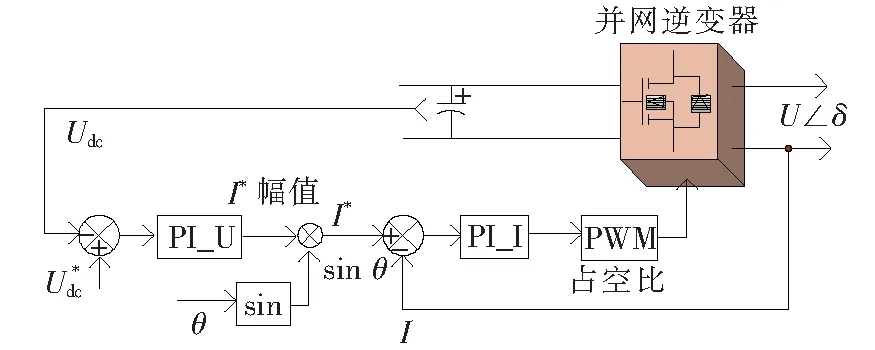
图3 2种控制方案下故障分析的IIDG表示法Figure 3 The IIDG representation of fault analysis under two control schemes

通过仿真含逆变型分布式电源的配电网，来分析电网发生故障时的故障特性。馈线末端故障时，逆变型分布式电源在双闭环控制下电流和电压波形如图4所示。故障后电流增加缓慢，并且缓慢下降回到稳态值，主要因为外部功率控制回路的响应速度较慢。如果不使用外部功率控制回路，只用内环电流控制则响应较快[13]。

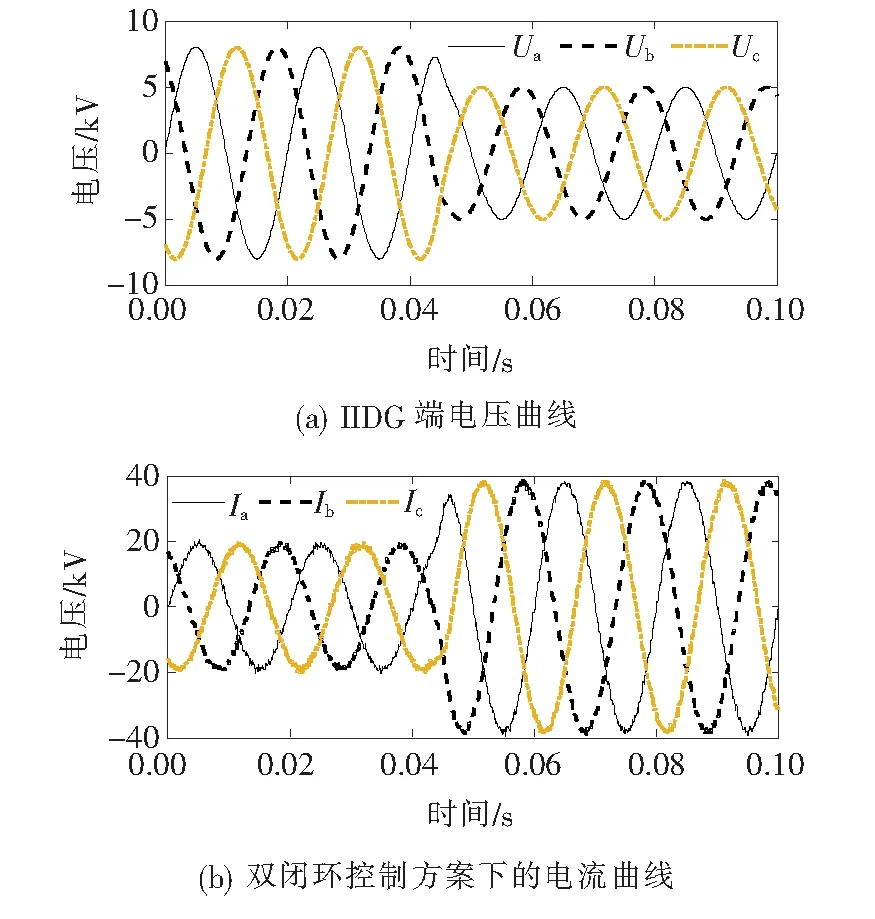
图4 IIDG在控制方案下故障响应Figure 4 IIDG wavefroms when responds to fault under control schemes

(4)

(5)

(6)

定义ηi和δi为第i个IIDG的正负序电流控制系数，则短路电流序分量为

(7)

(8)

含IIDG的配电网短路电流和端电压相互作用，如式(7)、(8)所示，IIDG短路电流也受端电压的影响。考虑IIDG双闭环控制，电网短路电流可采用式(4)～(8)计算，通过迭代方式有效求解。

2 配电网故障暂态电流计算模型

图4(b)的电流曲线可以分为2个过程，即第1周期电流峰值期间为次暂态过程，5～10周期为暂态过程；在故障的前几个周期中，IIDG的初始电流发生瞬变。因此，需要适合含IIDG的故障模型分析逆变器的故障响应并获取峰值电流，通过估计峰值电流的大小来确定保护装置承受的最大限值[15]，估计故障电流是否能够使保护装置动作断开IIDG。此外，如果IIDG未能及时切除并一直提供故障电流，还需要估计在前5～10个周期的暂态期间，IIDG故障电流对负荷侧电气设备的影响。本文所提方法的目标就是分析次暂态和暂态过程期间IIDG的动态响应，并获取故障的暂态特征。

2.1 IIDG故障次暂态过程分析

图4(a)所示故障导致馈线上的电压迅速下降，但是在次暂态期间几乎保持不变。电压下降导致IIDG的故障电流增加，逆变器参与控制降低电流。当电压变化不大时，可以使用传统故障分析方法，即通过稳态模型来估计峰值电流。

功率分布曲线如图5(a)所示，在此期间IIDG功率输出变化没有电流变化快，主要因为测量的有功功率是平均功率，而控制器在初始的半周期中不改变逆变器电压，如图5(b)所示。IIDG在其电流达到峰值的初始半周期电压保持恒定。因此，IIDG的次暂态峰值电流算法步骤如下。

图5 第1个周期内的IIDG功率和逆变器电压曲线Figure 5 IIDG power and inverter voltage curves in the first cycle

1)计算故障前配电网的节点电压为

(9)

3)计算每个IIDG的峰值电流为

(10)

2.2 IIDG故障暂态过程分析

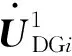
配电网状态方程为

(11)

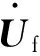
IIDG状态方程为

(12)

式中SDGi为分布式电源的视在功率。

1)配网等值模型。

(13)

(14)

(15)

图6 逆变器响应变化曲线Figure 6 Curves of inverter response variations

S(t)=Sn+(Sss,n+1-Sn)(1-e-t/τDG)

(16)

由此可用一阶模型近似在IIDG节点处的响应情况，通过计算在故障期间馈线模型中IIDG以外的戴维南等效阻抗Zf=Rf+jXf，并确定电路的相应时间常数，对S的变化进行更新。

2)IIDG控制模型。

在目前采用的IIDG控制器中通常应用的PI控制，因此可将其表示为传递函数，即

(17)

对控制器进行离散化，得到离散化控制器模型为

(18)

式中y、F分别为控制器输入和输出；T为时间步长。有功功率和无功功率误差作为给定2个PI控制器的输入，即实际功率与参考功率的差值。

3 仿真测试

为了测试所提出的故障分析方法的正确性，在IEEE 34节点馈线模型上进行了仿真，IEEE 34节点模型如图7所示。

图7 IEEE 34节点模型Figure 7 IEEE 34 node model

IIDG的容量为600 kV·A，输出电压为380 V，并通过△/Y变压器连接到电网，阻抗为3%，负荷以等效阻抗表示并集中在每段馈线末端，取UDG=1 p.u.，通过计算相应的IIDG电流来获得戴维南等效阻抗，以此估计相应的时间常数。

(19)

本文以馈线末端的三相平衡故障为例计算IIDG在次暂态和暂态过程的故障电流。首先计算在系统发生故障前的DG节点电压，给定DG功率输出，通过潮流计算确定节点电压和电流，并利用式(9)计算确定UDG，以初始误差xP=0、xQ=0做为控制器输入计算IDG在第1个周期中的峰值电流，进而计算配电网馈线响应。以UDG1=UDG1(t1)计算获得新的稳态节点电压Uss，并利用式(14)～(15)计算当前馈线的电流和功率值，以此估计t1时刻的IIDG电流值为

IDG1=IDG1+(Iss-DG1-IDG1)(1-e-T/τDG1)

(20)

通过PDG、QDG计算控制器的输入误差估计DG电压UDG1，并在t2～tn中迭代计算对结果进行更新。

3.1 IIDG三相对称故障分析

当节点846发生三相短路故障，采用本文所提方法获得的IIDG1电压和电流计算结果，如图8所示。结果表明：计算估计值与仿真测试电压非常接近，计算估计的故障电流能够很好地跟踪测试值，计算的峰值RMS电流为Ipeak-DG=21.5 A。计算的IIDG1暂态电流曲线比实际曲线更平滑，计算值在大约6个周期(100 ms)后非常接近测试值。本文所述方法可以准确地估计IIDG故障电流。

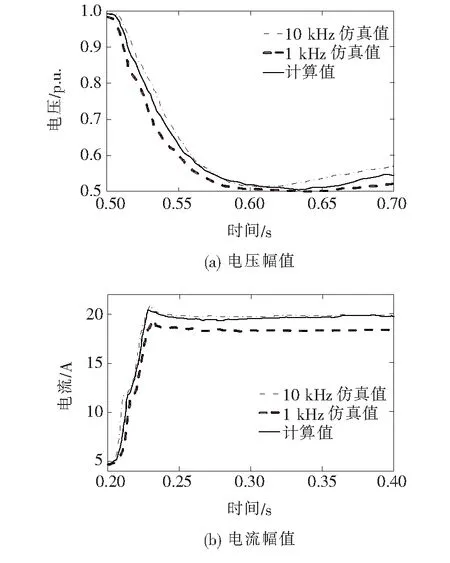
图8 IIDG逆变器电压电流(案例1)Figure 8 IIDG inverter voltage and current in (Case 1)

3.2 IIDG三相不对称故障分析

假定节点846发生单相接地故障。图9比较了IIDG在故障相的计算估计故障电流与仿真值，计算估计的故障电流可以跟随仿真测试值。因此，IIDG估计的第1个周期峰值电流为Ipeak-DG=28.2 A，与仿真的峰值电流非常接近。由图9可知，计算估计的电流值跟踪性能与三相对称故障情况下的跟踪性能大致相同。

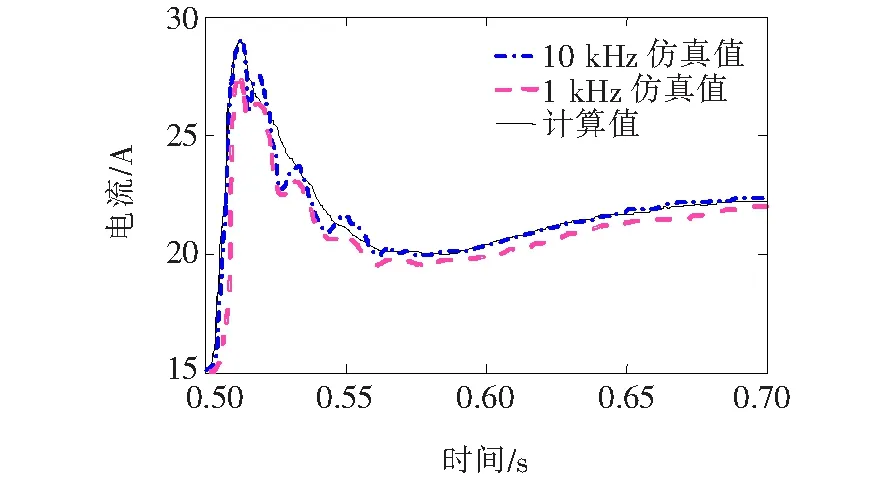
图9 IIDG故障电流曲线(案例2)Figure 9 Fault current curve for IIDG in (Case 2)

3.3 多IIDG故障分析

当IEEE 34节点模型上分布多个IIDG时，节点834发生单相对接地故障，测试节点位于IIDG1的电网侧。图10比较了IIDG2的故障相的计算故障电流与测试值。由图10可知，计算的故障电流与测试值差距较小。IIDG的第1个周期峰值RMS电流估计为Ipeak-DG=35.8 A，与仿真获得的峰值电流相近，由此体现了文本所提计算方法能够较为准确的对故障状态变量的计算。

图10 IIDG2故障电流曲线 Figure 10 Fault current curves for IIDG2

为了验证本文所提方法的正确性，计算不同故障位置下IIDG1的故障电流峰值，并与文献[15]中使用的方法对比。如表1所示，本文采用方法得到的短路电流可取得更小的误差。

表1 不同方法计算结果对比Table 1 Comparison between proposed nd reference method

4 结语

本文对含分布式电源的配电网次暂态和暂态故障电流计算方法进行了研究。在传统的故障分析方法基础上，提出了一种在故障期间获取IIDG故障特征的方法。所提方法给出了来自IIDG的故障电流和保护装置处的故障电流的RMS曲线，从而可以估计暂态期间的峰值电流和电流瞬变值。基于配网模型的仿真测试结果表明，所提出的方法可以准确地计算平衡和非平衡故障条件下的故障电流，该方法同样适用于多台IIDG接入电网的情况。